您现在的位置是:首页 >学无止境 >算法记录 | Day57 动态规划网站首页学无止境
算法记录 | Day57 动态规划
647.回文子串
思路:
1.确定dp数组(dp table)以及下标的含义:
布尔类型的dp[i][j]:表示区间范围[i,j] (注意是左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。
2.递推公式:
-
if (s[i]!=s[j])
dp[i][j] =False;
-
if (s[i]== s[j])
- i==j,同一个字符例如a,当然是回文子串
- abs(i-j)=1,例如aa,也是回文子串
- abs(i-j)>1,例如cabac,此时s[i]与s[j]已经相同了,看i到j区间是不是回文子串就看aba是不是回文就可以了,那么aba的区间就是 i+1 与 j-1区间,这个区间是不是回文就看
dp[i + 1][j - 1]是否为true。
3.初始化:dp[i][j]初始化为false
4.确定遍历顺序
首先从递推公式中可以看出,情况三是根据dp[i + 1][j - 1]是否为true,在对dp[i][j]进行赋值true的。
dp[i + 1][j - 1] 在 dp[i][j]的左下角,如图:
要从下到上,从左到右遍历,这样保证dp[i + 1][j - 1]都是经过计算的。
!5.举例推导dp数组
举例,输入:“aaa”,dp[i][j]状态如下:

图中有6个true,所以就是有6个回文子串。
注意因为dp[i][j]的定义,所以j一定是大于等于i的,那么在填充dp[i][j]的时候一定是只填充右上半部分。](https://code-thinking-1253855093.file.myqcloud.com/pics/20210121171032473-20230310132134822.jpg)
class Solution:
def countSubstrings(self, s: str) -> int:
size = len(s)
if size <= 1:
return size
dp =[[False]*size for _ in range(size)]
result = 0
for i in range(size+1,-1,-1):
for j in range(i,size):
if s[i] == s[j]:
if (j-i) <= 1:
dp[i][j] = True
result += 1
elif(dp[i+1][j-1]):
dp[i][j] = True
result += 1
return result
516.最长回文子序列
思路:
1.确定dp数组(dp table)以及下标的含义
dp[i][j]:字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。
2.确定递推公式
- if(s[i]==s[j]),
dp[i][j] = dp[i + 1][j - 1] + 2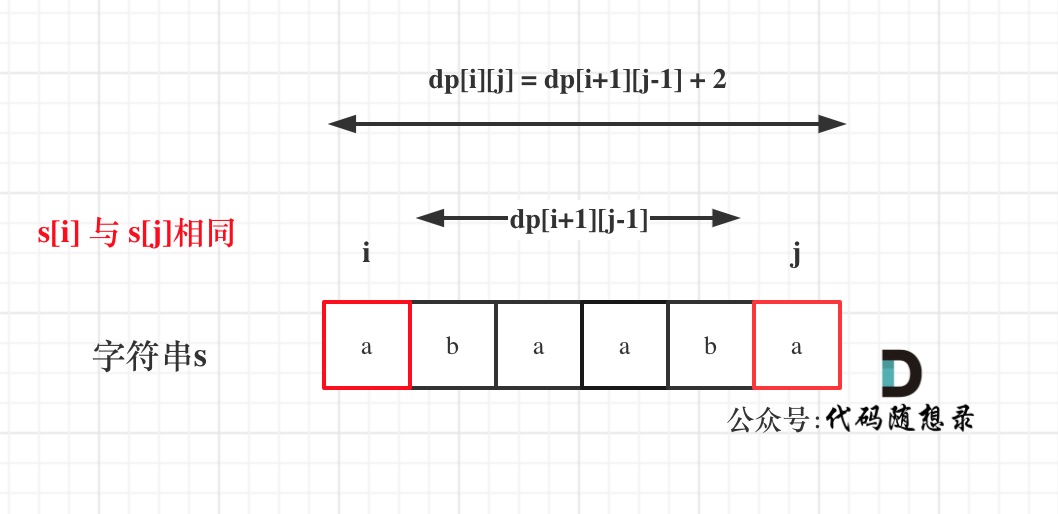
- if(s[i]!=s[j]),
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])- 加入s[j]的回文子序列长度为
dp[i + 1][j]。 - 加入s[i]的回文子序列长度为
dp[i][j - 1]。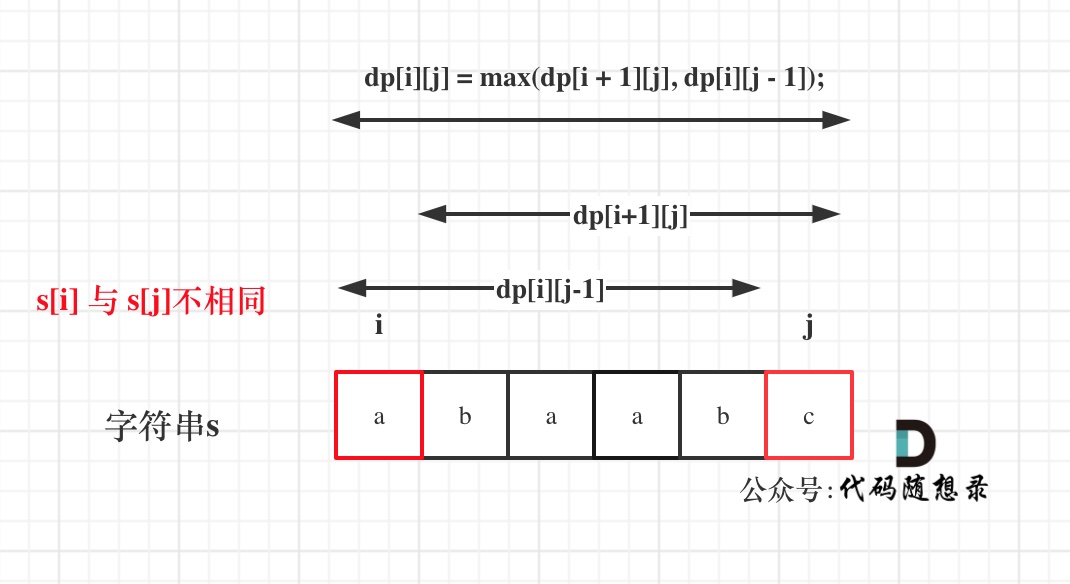
- 加入s[j]的回文子序列长度为
3.初始化:当i与j相同,那么dp[i][j]一定是等于1的,即:一个字符的回文子序列长度就是1。
4.确定遍历顺序
从递归公式中,可以看出,dp[i][j] 依赖于 dp[i + 1][j - 1],dp[i + 1][j] 和 dp[i][j - 1],如图:
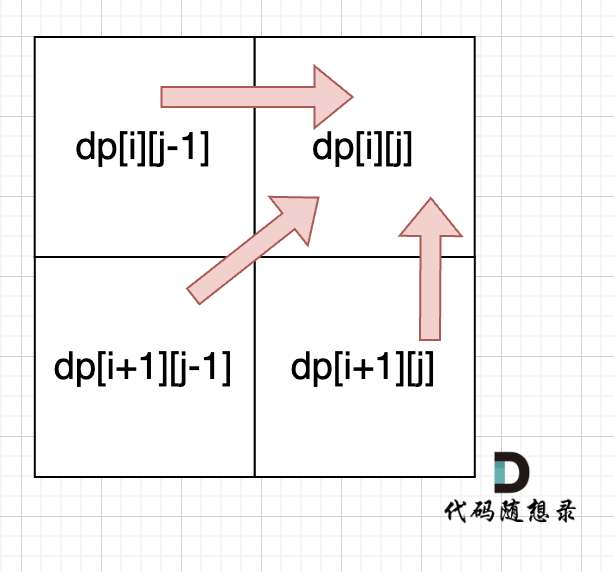
所以遍历i的时候一定要从下到上遍历,这样才能保证下一行的数据是经过计算的
5.举例推导dp数组
输入s:“cbbd” 为例,dp数组状态如图:红色框即:dp[0][-1]为最终结果。
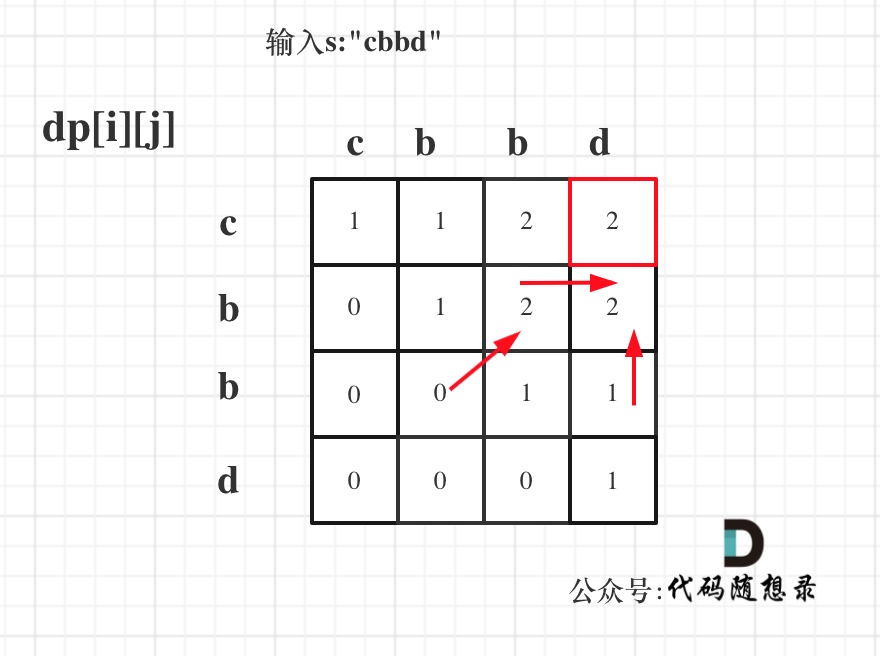
class Solution:
def longestPalindromeSubseq(self, s: str) -> int:
size = len(s)
if size <= 1:
return size
dp = [[0]*size for _ in range(size)]
for i in range(size):
dp[i][i] = 1
for i in range(size-1,-1,-1):
for j in range(i+1, size):
if (s[i]==s[j]):
dp[i][j] = dp[i+1][j-1] + 2
else:
dp[i][j] = max(dp[i+1][j],dp[i][j-1])
return dp[0][-1]
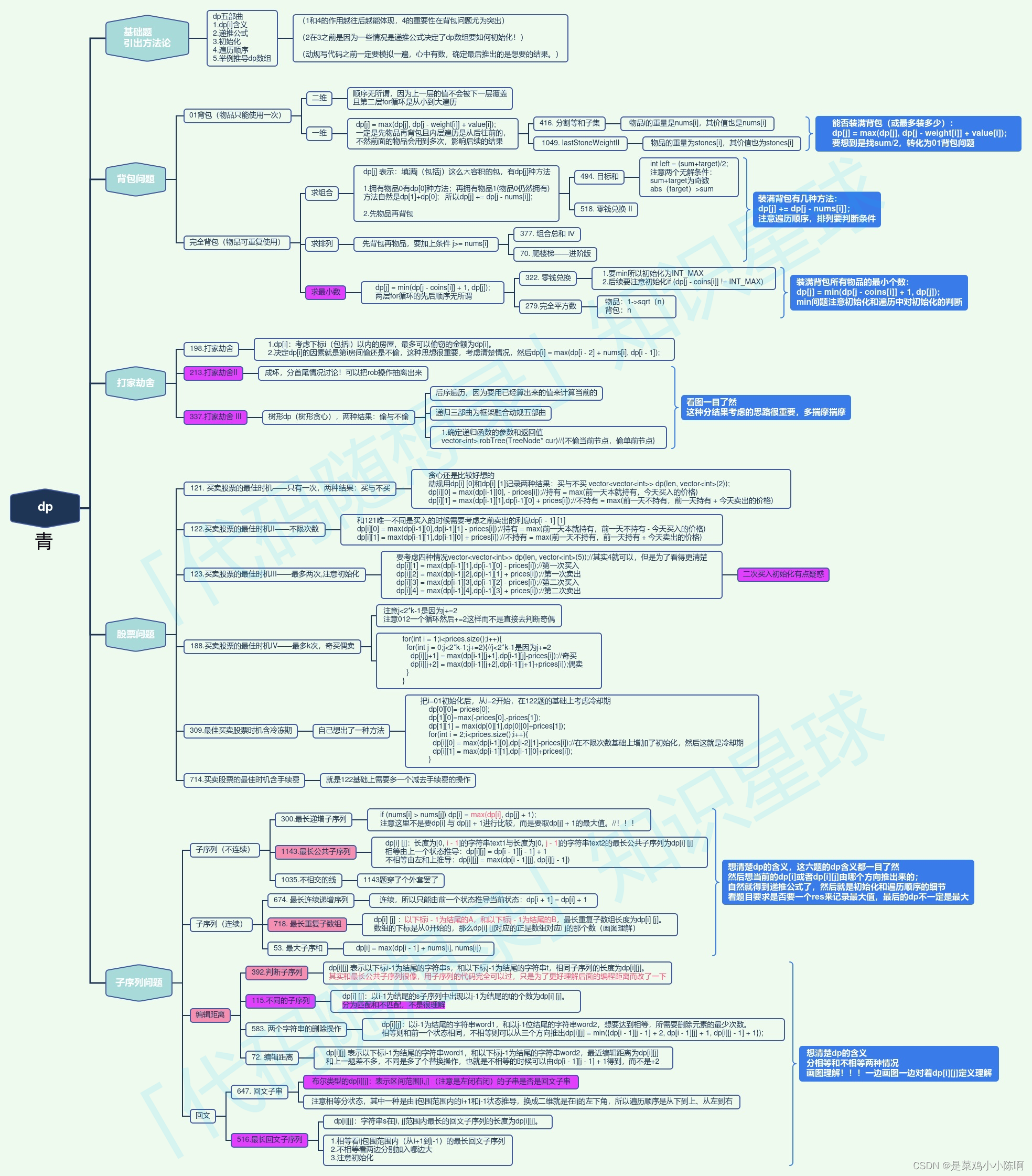
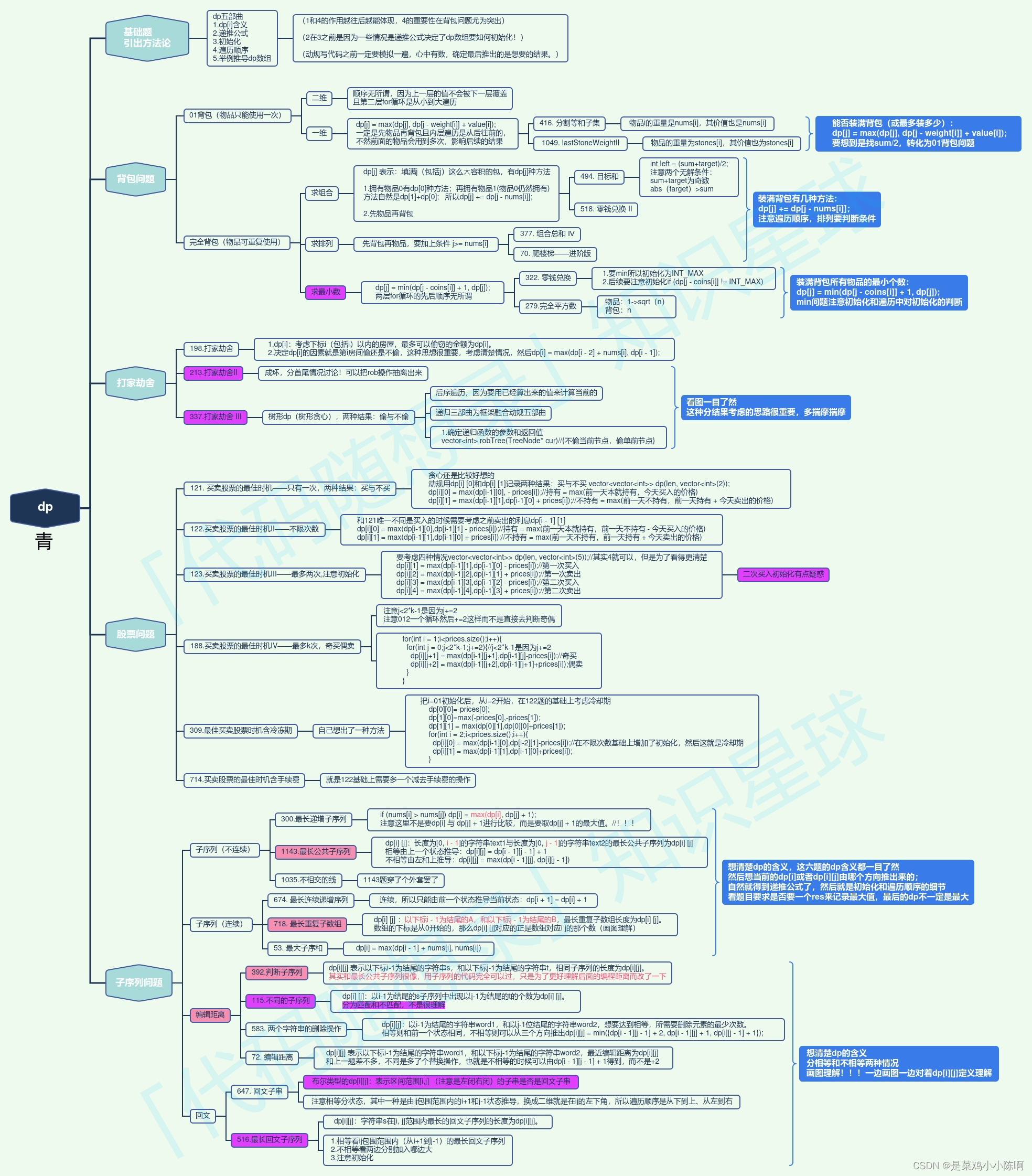
动态规划总结
动规五部曲分别为:
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组






 U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) Allegro16.6差分等长设置及走线总结
Allegro16.6差分等长设置及走线总结