您现在的位置是：首页 >技术教程 >【算法与数据结构】链表网站首页技术教程
【算法与数据结构】链表
简介【算法与数据结构】链表
链表
链表：结构定义
链表是由一串节点串联在一起的，链表的每个节点存储两个信息：数据+下一个节点的地址
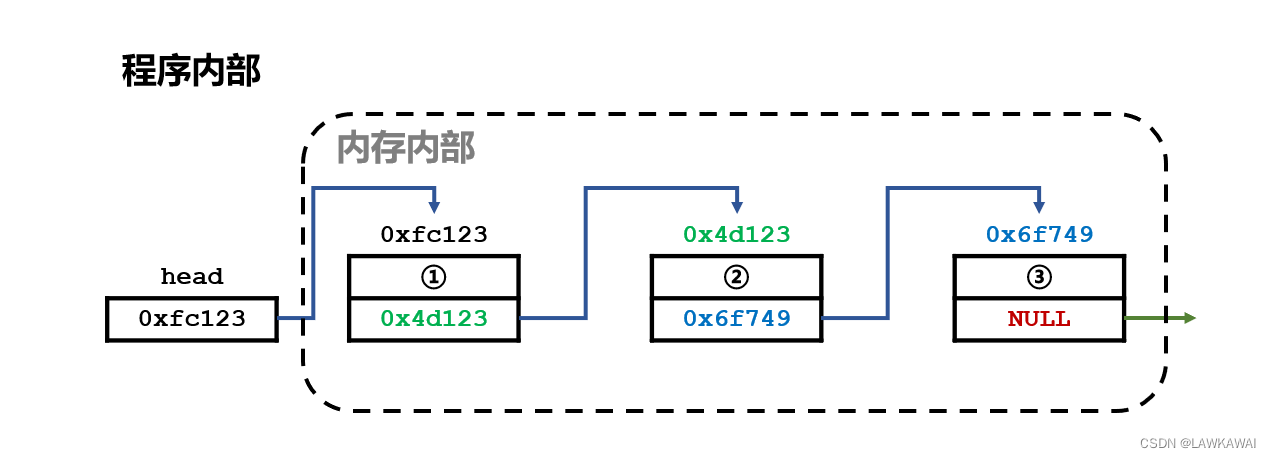
分清楚两个概念：什么是内存内部，什么是程序内部
内存内部： 信息存储在内存空间里的
程序内部： 通过什么信息，去操作结构
如果想操作链表的话，我们依靠的是程序内部的信息，而不是内存内部的信息；所以在操作过程中，这些程序内部信息千万不能丢了，因为如果一旦丢了，那么对于内存内部的信息，就永远失去了访问的权限。
代码
结构定义
typedef struct Node{
int data;
struct Node *next;
} Node;
构造节点
Node * getNewNode(int val)
{
Node *p = (Node*)malloc(sizeof(Node));
p->data = val;
p->next = NULL; // 新的节点的下一个指向空
return p;
}
删除链表
循环遍历节点，先用一个指针p指向头节点，因为先需要移动到下一个节点，再销毁前一个指针，所以需要一个q指针来记录下一个节点，然后销毁当前节点指针p
void clear(Node *head)
{
if (head == NULL) return;
// 循环遍历链表中每个节点, 当遍历不为空，就一直向后走
for (Node *p = head, *q; p; p = q) // p是当前节点
{
q = p->next; // 先让q指向下一个节点
free(p); // 再销毁当前节点
}
return;
}
链表：插入元素
插入过程的操作顺序，直接影响了我们是否能正确插入一个元素
程序内部信息：head变量：指向整个链表的头地址，node变量：指向待插入的新节点
需要把4号节点插入到2节点后面
首先，需要一个指针p, 需要找到待插入位置的前一个元素，即1号节点，p指向1号元素
然后，让新的节点(4号节点)指向2号元素
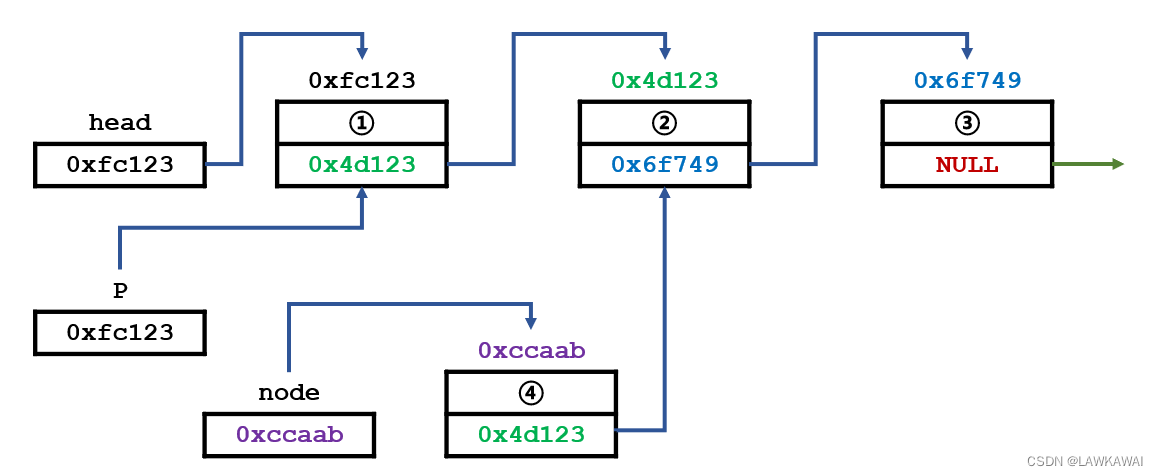
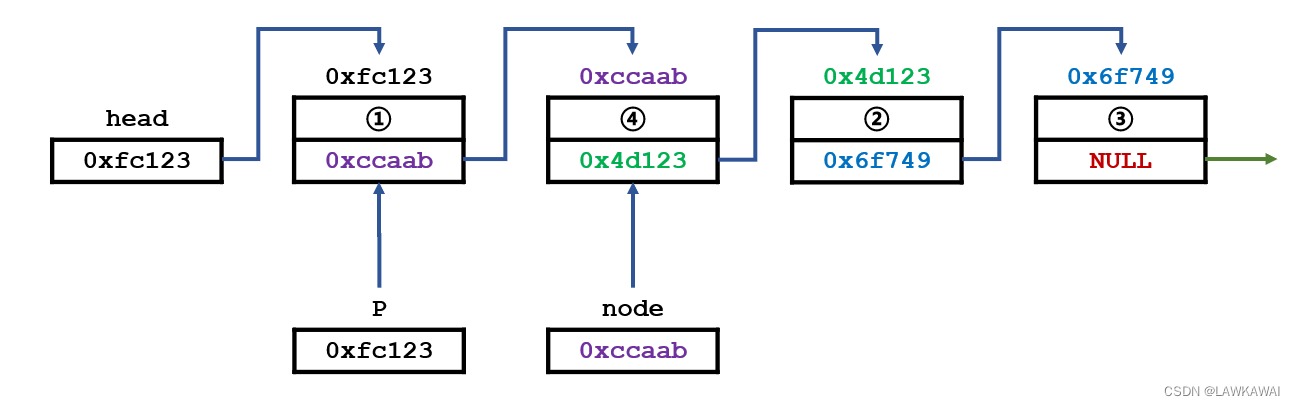
然后，让1号元素指向新的节点(4号元素)：
此时，在逻辑结构上，就已经完成了插入操作：
代码
因为这是无头链表结构，在实现插入操作的时候，返回的是完成插入之后新链表的首地址
无头链表插入操作后链表的首地址是可能发生改变的。
第一种情况：链表为空，或者插入的位置是0位置（原来链表头的位置），就会导致整个链表的头地址发生改变 ，直接返回新节点
第二种情况： 链表不为空，且插入位置在0之后，就是一般的插入操作，返回原链表头节点指针
p指针是用来找到待插入指针的前一个元素
Node * insert(Node *head, int pos, int val)
{
if (pos == 0)
{
Node *node = getNewNode(val); // 先创建新节点
node->next = head; // 让新节点指向原来的头节点
return node; // 直接返回新节点
}
Node *p = head; // p找到待插入位置的前一个元素
for (int i = 1; i < pos; i++) p = p->next; // p走到待插入位置的前一个位置
Node *node = getNewNode(val); // 创建新节点
node->next = p->next; // 先让新节点的next指向待插入位置的节点，即p->next
p->next = node; // 再让p的next指向新节点
// 此时逻辑上已经完成了插入的操作
return head; // 返回原链表头节点
}
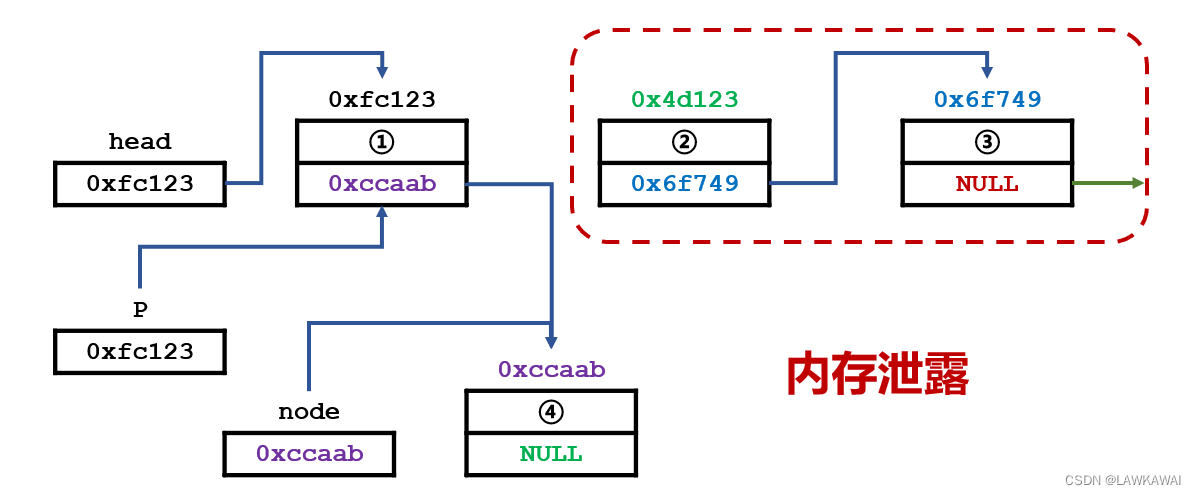
链表：错误插入
由于链表的插入很容易犯错，这里演示一个错误的插入操作
先找到待插入位置的前一个元素
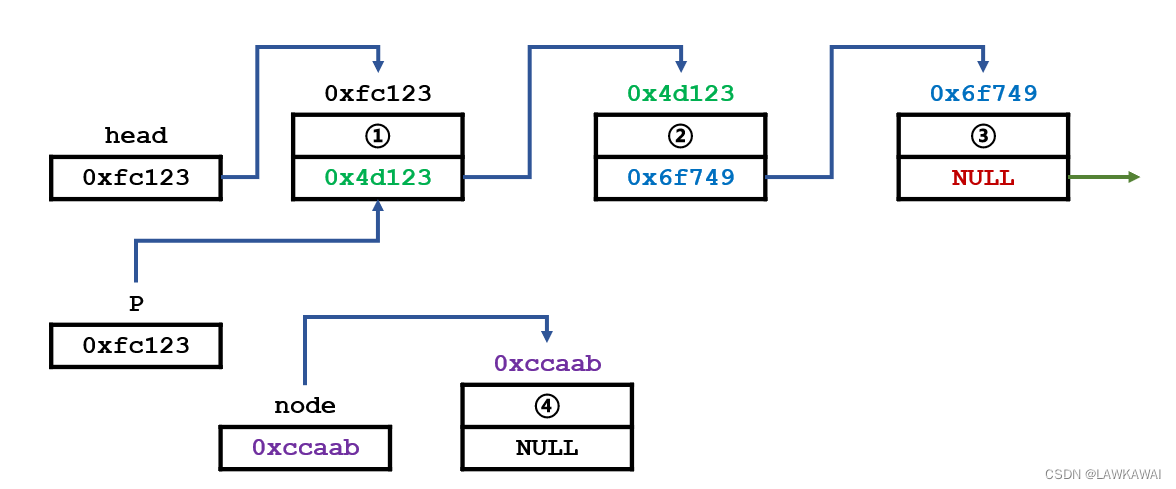
正确的插入顺序是，让新的元素指向2号元素；错误的操作是，让1号元素（待插入元素的前一个元素）指向新的元素(4号元素)，那么就会发现2号元素的地址信息丢失了，也就是发生内存泄漏。
内存泄漏： 其实写的所有程序都占用内存空间，2号元素和3号元素，依然占用着我们的内存空间，但在程序中对这段信息没有办法进行操作。
对于中大型需要长期线上运行的系统，需要对内存泄漏的问题及其关注和避免的。
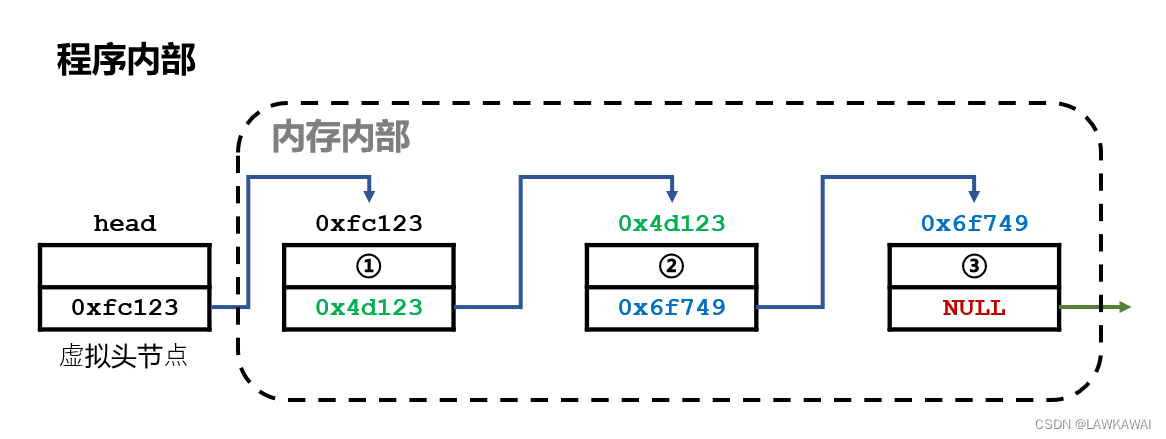
链表：无头链表
在头部是不存储信息的，所以在链表的头部存储的仅仅是一个指针。
链表：有头链表
在头部存储信息，在链表的头部存储的是一个节点。只不过这个节点有存储数据的区域，但我们不使用这个区域
虚拟头节点： 一般就是有头链表的头节点
代码演示
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <iostream>
typedef struct Node{
int data;
struct Node *next;
} Node;
Node * getNewNode(int val)
{
Node *p = (Node*)malloc(sizeof(Node));
p->data = val;
p->next = NULL; // 新的节点的下一个指向空
return p;
}
Node *insert(Node *head, int pos, int val)
{
if (pos == 0)
{
Node *node = getNewNode(val); // 先创建新节点
node->next = head; // 让新节点指向原来的头节点
return node; // 直接返回新节点
}
Node *p = head; // p找到待插入位置的前一个元素
for (int i = 1; i < pos; i++) p = p->next; // p走到待插入位置的前一个位置
Node *node = getNewNode(val); // 创建新节点
node->next = p->next; // 先让新节点的next指向待插入位置的节点，即p->next
p->next = node; // 再让p的next指向新节点
// 此时逻辑上已经完成了插入的操作
return head; // 返回原链表头节点
}
void clear(Node *head)
{
if (head == NULL) return;
// 循环遍历链表中每个节点, 当遍历不为空，就一直向后走
for (Node *p = head, *q; p; p = q) // p是当前节点
{
q = p->next; // 先让q指向下一个节点
free(p); // 再销毁当前节点
}
return;
}
void output_linklist(Node *head)
{
// 0 1 2
// 22->33->55
int n = 0;
for (Node *p = head; p; p = p->next) n += 1; // 先求链表的长度n
// 打印第一行序号
for (int i = 0; i < n; i++)
{
printf("%3d", i);
printf(" "); // 对应链表的->两个字符
}
printf("
");
// 打印第二行链表
for (Node *p = head; p; p = p->next)
{
printf("%3d", p->data);
printf("->");
}
printf("
");
return;
}
int main()
{
srand(time(0));
#define MAX_OP 7
Node *head = NULL;
for (int i = 0; i < MAX_OP; i++)
{
int pos = rand() % (i + 1), val = rand() % 100; // 这里的第一个pos因为是随机数对1取余，永远都是0
printf("insert %d at %d to linklist
", val, pos);
head = insert(head, pos, val);
output_linklist(head);
}
std::cin.get();
return 0;
}
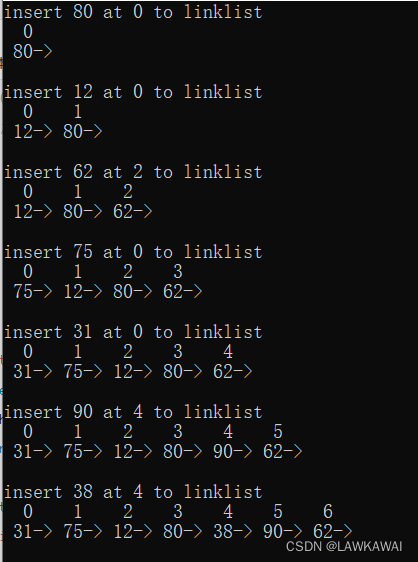
输出：
链表：花式查找操作的实现
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <iostream>
#define DL 3
#define STR(n) #n
#define DIGIT_LEN_STR(n) "%" STR(n) "d"
typedef struct Node{
int data;
struct Node *next;
} Node;
Node * getNewNode(int val)
{
Node *p = (Node*)malloc(sizeof(Node));
p->data = val;
p->next = NULL; // 新的节点的下一个指向空
return p;
}
Node *insert(Node *head, int pos, int val)
{
if (pos == 0)
{
Node *node = getNewNode(val); // 先创建新节点
node->next = head; // 让新节点指向原来的头节点
return node; // 直接返回新节点
}
Node *p = head; // p找到待插入位置的前一个元素
for (int i = 1; i < pos; i++) p = p->next; // p走到待插入位置的前一个位置
Node *node = getNewNode(val); // 创建新节点
node->next = p->next; // 先让新节点的next指向待插入位置的节点，即p->next
p->next = node; // 再让p的next指向新节点
// 此时逻辑上已经完成了插入的操作
return head; // 返回原链表头节点
}
void clear(Node *head)
{
if (head == NULL) return;
// 循环遍历链表中每个节点, 当遍历不为空，就一直向后走
for (Node *p = head, *q; p; p = q) // p是当前节点
{
q = p->next; // 先让q指向下一个节点
free(p); // 再销毁当前节点
}
return;
}
void output_linklist(Node *head, int flag = 0)
{
// 0 1 2
// 22->33->55
int n = 0;
for (Node *p = head; p; p = p->next) n += 1; // 先求链表的长度n
// 打印第一行序号
for (int i = 0; i < n; i++)
{
// printf("%3d", i);
printf(DIGIT_LEN_STR(DL), i);
printf(" "); // 对应链表的->两个字符
}
printf("
");
// 打印第二行链表
for (Node *p = head; p; p = p->next)
{
// printf("%3d", p->data);
printf(DIGIT_LEN_STR(DL), p->data);
printf("->");
}
printf("
");
if (flag == 0) printf("
");
return;
}
int find(Node *head, int val)
{
// 查找，遍历链表的每个节点
Node *p = head; // 当前节点指针
int n = 0; // 用来记录输出元素个数
while (p)
{
if (p->data == val){
output_linklist(head, 1);
int len = n * (DL + 2); // 空字符个数
for (int i = 0; i < len; i++) printf(" "); // 输出前面的空格
printf("^
");
for (int i = 0; i < len; i++) printf(" "); // 输出前面的空格
printf("|
");
return 1;
}
n += 1;
p = p->next;
}
return 0;
}
int main()
{
srand(time(0));
#define MAX_OP 7
Node *head = NULL;
// 测试插入操作
for (int i = 0; i < MAX_OP; i++)
{
int pos = rand() % (i + 1), val = rand() % 100; // 这里的第一个pos因为是随机数对1取余，永远都是0
printf("insert %d at %d to linklist
", val, pos);
head = insert(head, pos, val);
output_linklist(head);
}
// 测试查找操作
int val;
while (scanf_s("%d", &val)){
if (!find(head, val)) printf("not found
");
}
std::cin.get();
return 0;
}
输出链表的生成：
输出查找操作
链表：用有头链表改写插入操作
定义一个虚拟头节点，然后定义一个指针p，指向虚拟头节点
让虚拟头节点的下一节点为原来的头指针，此时形成了一个有头链表
然后开始插入操作，一样的，先找到待插入位置的前一个元素位置，这时候因为在0位置前有一个虚拟头节点，所以对于pos=0的情况，就是虚拟头节点本身。
注意：虚拟头节点的下一个节点才是要返回的头节点
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <iostream>
#define DL 3
#define STR(n) #n
#define DIGIT_LEN_STR(n) "%" STR(n) "d"
typedef struct Node{
int data;
struct Node *next;
} Node;
Node * getNewNode(int val)
{
Node *p = (Node*)malloc(sizeof(Node));
p->data = val;
p->next = NULL; // 新的节点的下一个指向空
return p;
}
// 有头链表的插入操作
Node *insert(Node *head, int pos, int val)
{
Node newhead, *p = &newhead;
newhead.next = head; // 让虚拟头节点的下一节点为head
// 此时已经构造了一个有头链表
for (int i = 0; i < pos; i++) p = p->next; // 先找到待插入位置的前一位
Node *node = getNewNode(val);
node->next = p->next;
p->next = node;
return newhead.next; // 虚拟头节点的下一个节点才是要返回的头节点
}
void clear(Node *head)
{
if (head == NULL) return;
// 循环遍历链表中每个节点, 当遍历不为空，就一直向后走
for (Node *p = head, *q; p; p = q) // p是当前节点
{
q = p->next; // 先让q指向下一个节点
free(p); // 再销毁当前节点
}
return;
}
void output_linklist(Node *head, int flag = 0)
{
// 0 1 2
// 22->33->55
int n = 0;
for (Node *p = head; p; p = p->next) n += 1; // 先求链表的长度n
// 打印第一行序号
for (int i = 0; i < n; i++)
{
// printf("%3d", i);
printf(DIGIT_LEN_STR(DL), i);
printf(" "); // 对应链表的->两个字符
}
printf("
");
// 打印第二行链表
for (Node *p = head; p; p = p->next)
{
// printf("%3d", p->data);
printf(DIGIT_LEN_STR(DL), p->data);
printf("->");
}
printf("
");
if (flag == 0) printf("
");
return;
}
int find(Node *head, int val)
{
// 查找，遍历链表的每个节点
Node *p = head; // 当前节点指针
int n = 0; // 用来记录输出元素个数
while (p)
{
if (p->data == val){
output_linklist(head, 1);
int len = n * (DL + 2) + 1; // 空字符个数
for (int i = 0; i < len; i++) printf(" "); // 输出前面的空格
printf("^
");
for (int i = 0; i < len; i++) printf(" "); // 输出前面的空格
printf("|
");
return 1;
}
n += 1;
p = p->next;
}
return 0;
}
int main()
{
srand(time(0));
#define MAX_OP 7
Node *head = NULL;
// 测试插入操作
for (int i = 0; i < MAX_OP; i++)
{
int pos = rand() % (i + 1), val = rand() % 100; // 这里的第一个pos因为是随机数对1取余，永远都是0
printf("insert %d at %d to linklist
", val, pos);
head = insert(head, pos, val);
output_linklist(head);
}
// 测试查找操作
int val;
while (scanf_s("%d", &val)){
if (!find(head, val)) printf("not found
");
}
std::cin.get();
return 0;
}
链表：循环链表
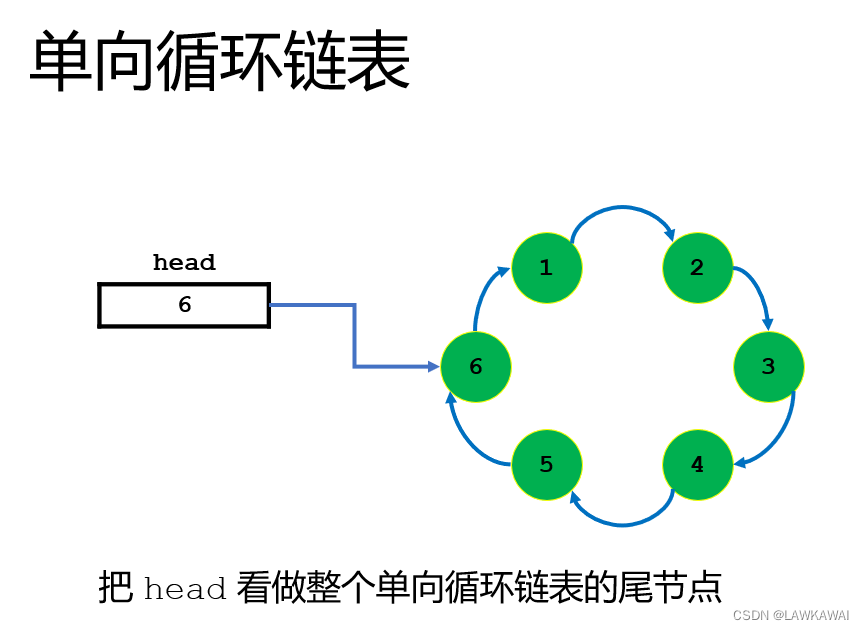
单向循环链表
单向循环链表：在单向链表的基础上加一个循环结构，循环结构是指最后一个节点指向了第一个节点
注意： 在单向循环链表中的头指针head指向整个链表的最后一个节点
为什么要指向最后一个节点：因为最后一个节点充当着一个实实在在的链表中的节点，也充当着一个虚拟头节点。有了这个虚拟头节点之后，当需要插入节点到链表中时，插入到哪个位置就向后走几步即可
代码
结构定义
与单向链表的节点定义一样
typedef struct Node{
int data;
struct Node *next;
} Node;
构造循环
Node *ConstructLoop(Node *head) // 构造链表循环
{
if (head == NULL) return head;
Node *p = head;
while (p->next) p = p->next; // 找到链表的最后一个节点
p->next = head; //最后的节点的下一个节点指向头节点
head = p; // 头指针指向最后一个节点
return head; // 返回头指针
}
删除循环链表
与单向链表的删除一样
void clear(Node *head) // 删除单向链表
{
if (head == NULL) return;
// 循环遍历链表中每个节点, 当遍历不为空，就一直向后走
for (Node *p = head, *q; p; p = q) // p是当前节点
{
q = p->next; // 先让q指向下一个节点
free(p); // 再销毁当前节点
}
return;
}
单向循环链表：插入
如果头指针head指向的不是链表最后一个节点，而是第一个节点，那么在插入元素到index=0的位置时，是不是要先找到0位置节点的前一个节点，那就是链表的最后一个节点，也就是说，为了在0位置插入一个节点，还要先遍历完链表的全部节点才能进行插入操作，所以将头指针head设置为链表最后一个节点是合理。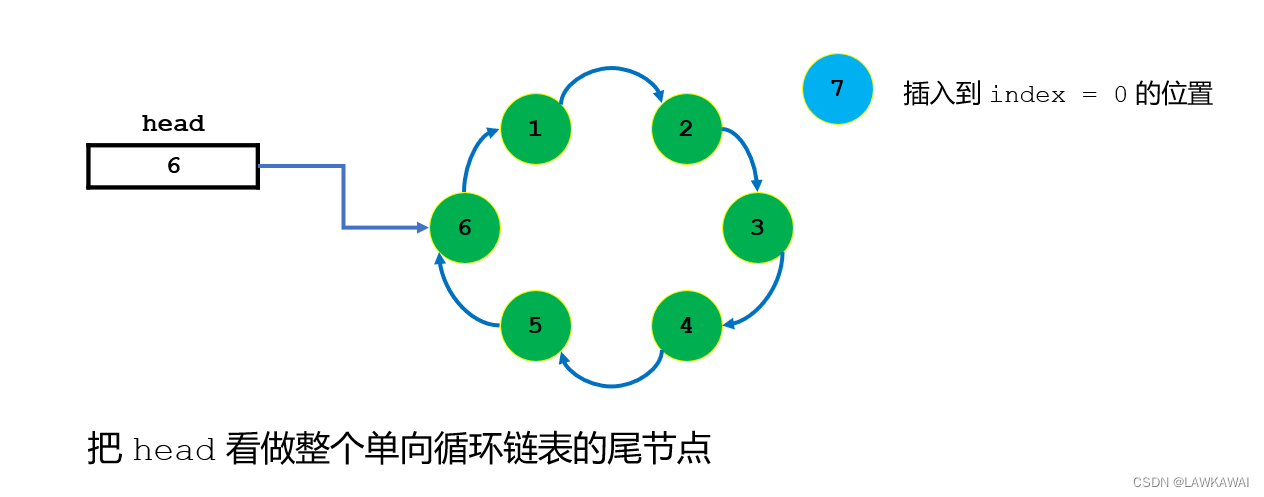
插入在index=0位置后，不需要修改head指向的节点，保持指向为最后一个节点即可。
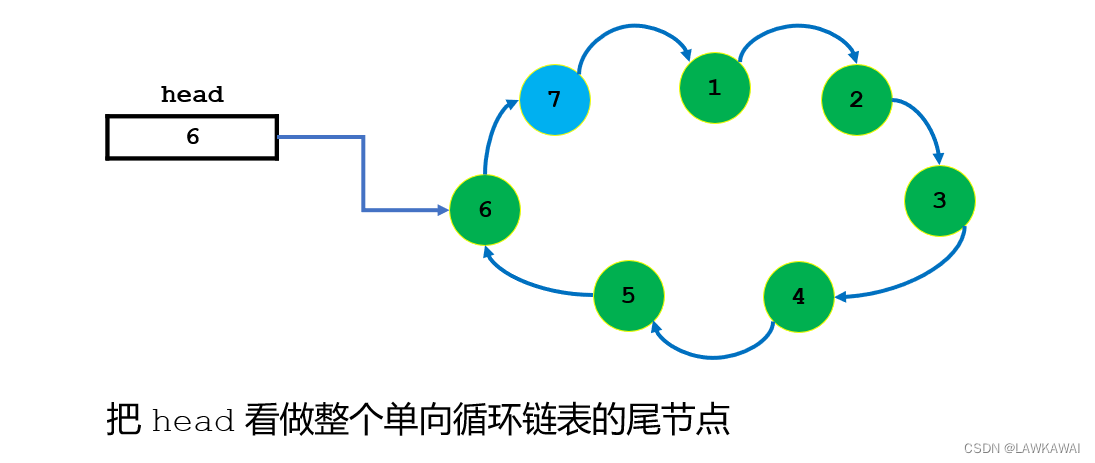
插入到链表的最后一个节点的后面，则需要在插入完成后修改head指向的节点
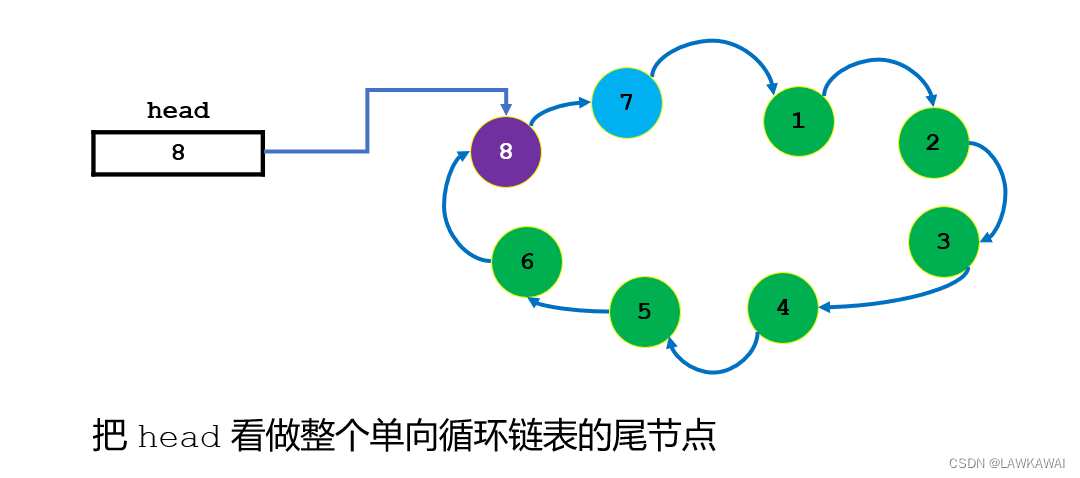
代码
Node *insertLoop(Node *head, int pos, int val)
{
int n = 1;
Node *q = head->next;
while (q != head) // 记录循环链表的长度
{
n += 1;
q = q->next;
}
Node *p = head; // 当前指针指向头节点，相当于单向链表的虚拟头节点
for (int i = 0; i < pos; i++) p = p->next; // 找到待插入位置的前一位
Node *node = getNewNode(val);
// 插入操作
if (pos < n)
{
node->next = p->next;
p->next = node;
return head; // 如果插入的位置不是在最后一个节点之后，返回原头指针
}
else
{
node->next = p->next;
p->next = node;
head = node; // 否则，头指针指向最后一个节点
return head;
}
}
链表：双向链表
双向链表： 除了有指向下一个节点的变量next指针之外，还有指向上一个节点的变量pre指针
第一个节点的pre指针指向空地址
最后一个节点的next指针指向空地址
代码
结构定义
typedef struct BiNode{
int data;
struct BiNode *next;
struct BiNode *pre;
} BiNode;
构造节点
BiNode *getNewBiNode(int val)
{
BiNode *p = (BiNode*)malloc(sizeof(BiNode));
p->data = val;
p->next = NULL;
p->pre = NULL;
return p;
}
删除双向链表
与单向链表的删除一样
void clear(Node *head) // 删除单向链表
{
if (head == NULL) return;
// 循环遍历链表中每个节点, 当遍历不为空，就一直向后走
for (Node *p = head, *q; p; p = q) // p是当前节点
{
q = p->next; // 先让q指向下一个节点
free(p); // 再销毁当前节点
}
return;
}
风语者！平时喜欢研究各种技术，目前在从事后端开发工作，热爱生活、热爱工作。
站长推荐
- U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 - stm32使用HAL库配置串口中断收发数据（保姆级教程）
stm32使用HAL库配置串口中断收发数据（保姆级教程） - SpringSecurity实现前后端分离认证授权
SpringSecurity实现前后端分离认证授权 - 【社区图书馆】伴我前行的一本书《The C Programming Language》
【社区图书馆】伴我前行的一本书《The C Programming Language》 - 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效)