您现在的位置是:首页 >学无止境 >数据结构 (入门必看)网站首页学无止境
数据结构 (入门必看)
一、 预备知识
(一)数据结构前言
1、学习C语言是如何写程序,学习数据结构如何简洁高效的写程序
2、遇到一个实际问题,需要写程序,需要解决两个方面的问题
1)如何表达数据之间的逻辑规律以及如何将数据存储到计算机中
数据结构
数据:不是单纯的数值,而是一个类似于集合的概念(结构体(节点))
结构:数据之间的关系
2)采用什么样的方法来解决问题:算法(冒泡排序、选择排序、顺序查找)
数据结构 + 算法 = 程序
3. 数据结构
数据的逻辑结构、存储结构及操作
3.1 数据
数据:不是单纯的数值,而是一个类似于集合的概念
数据元素:数据元素是数据的基本单位,数据元素由若干个基本项组成
数据项:数据元素由若干个数据项组成,数据项是数据的最小单位
节点:数据元素又叫节点
(二)逻辑结构
逻辑结构及数据之间的关系
逻辑结构:数据与数据之间的联系和规律 逻辑关系
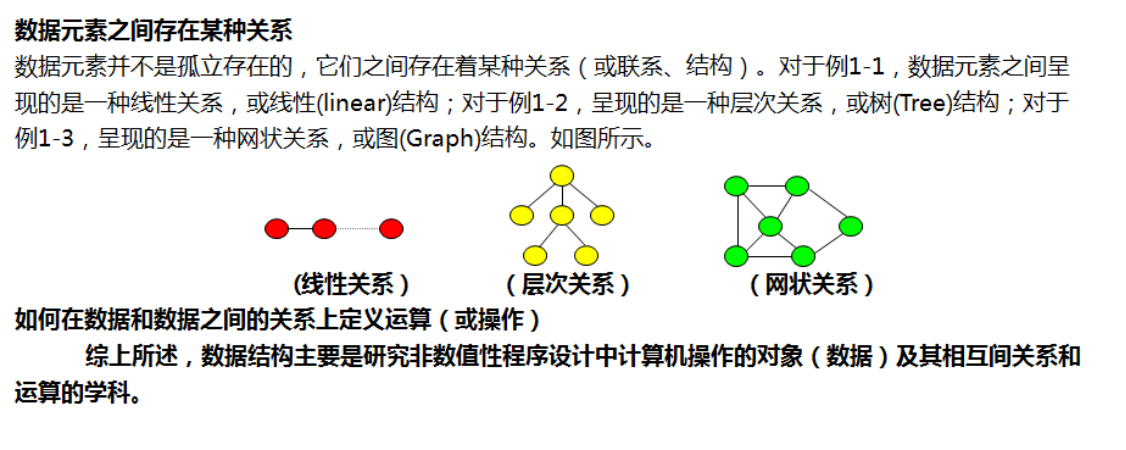
数据之间的关系:
1、线性关系
线性关系------> 线性结构 -----> 一对一 ------>顺序表(数组)、链表(指针)、 栈、队列(队头出队、队尾入队)
2、层次关系
层次关系------> 树形结构 -----> 一对多 ------> 树
3、网状关系
网状关系------> 图状结构 -----> 多对多 ------> 图
(三)存储结构
存储类型
存储结构:数据的存储结构指的是数据的逻辑结构在计算机存储器中的映象(或表示)。存储结构是通过计算机语言所编制的程序来实现的,因而是依赖于具体的计算机语言。int a ,int st[] ; 结构体;
1、顺序存储结构
数组:将数据结构中各元素按照其逻辑顺序存放于存储器一片连续的存储空间中(如c语言的一维数组)

2、链式存储结构
特点:数据在内存当中存储是不连续的,通过指针将数据联系在一起
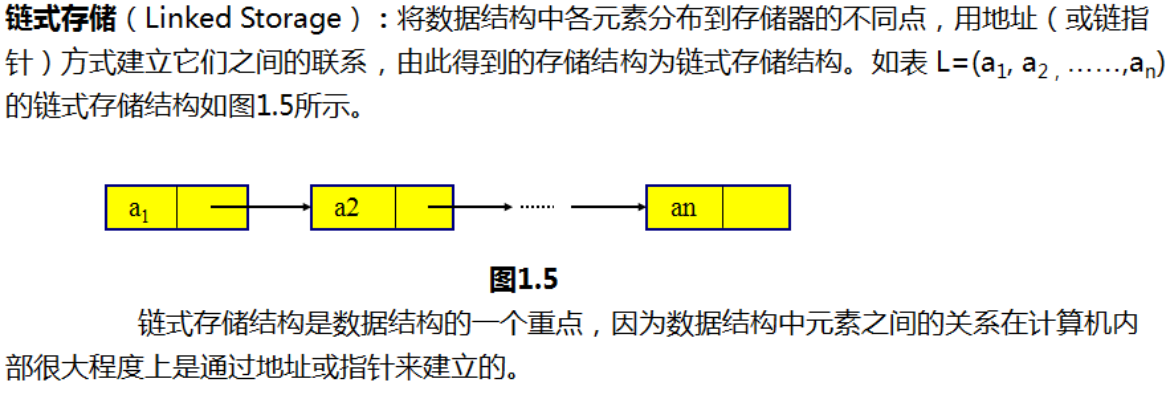
struct node_t stu ->stu.data; stu.next = &a2
struct node_t *p ; p->data; p->next; (data和next:结构体成员)
链表:
struct node_t
{
int data;//数据域
struct node_t *next;//指向自身结构体类型
};
先定义结构体类型,再定义这种类型所对应的变量(变量、数组、指针)
点运算符(.)用于结构体变量访问成员。
箭头运算符(->)用于结构体指针变量访问成员。
struct node_t a1;
struct node_t a2;
struct node_t *a3;
struct node_t a4;
a1.next = &a2;
a2.next = a3;
a3->next = &a4
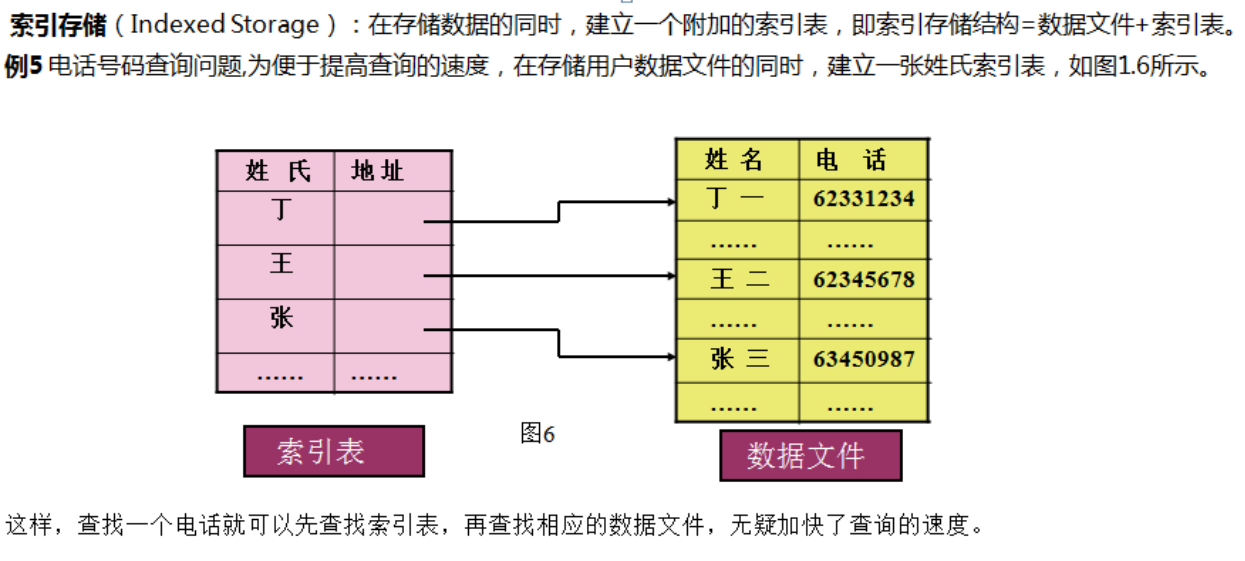
3、索引存储结构
提高查找速度
索引表 + 数据文件
姓氏+ 地址 名字 + 电话号码
4、散列存储结构
数据在存储的时候与关键码之间存在某种对应关系,存的时候按照对应关系存,取的时候按照对应关系取
(四)操作 (运算)
增删改查
图书管理系统
查找某个图书信息
新买一本书,增加到数据中
书丢了,删除
书名写错了,修改
(五)算法
算法衡量标准
解决问题的思想办法 (冒泡排序、选择排序、快速排序)
1、 算法与程序
算法:解决问题的思想办法
程序:用计算机语言对算法的具体实现
2、算法与数据结构
算法 + 数据结构 = 程序 (进程、程序)
算法的设计: 取决于选定的逻辑结构(线性、参差、网状)
算法的实现: 依赖于采用的存储结构 (顺序、链式、索引、散列)
3、算法的特性
(1)有穷性 :算法的执行步骤是有限的
(2)确定性 :算法的每一个步骤,无二义性 ,没有歧义
(3)可行性 :算法能够在有限的时间内完成
(4)输入 :一个算法可以有一个或多个输入
(5)输出 :一个算法可以有一个或多个输出
4、如何评价一个算法的好坏
(1)消耗时间的多少 越少越好
(2)消耗内存的多少 越小越好
(3)程序的可读性 、维护、调试 、移植 好坏
5、 时间复杂度(程序运行的速度)
定义:算法的可执行语句重复执行的频度和
语句频度: 算法中可执行语句重复执行的次数
通常时间复杂度用一个问题规模函数来表达 :
T(n) = O(f(n))
T(n) :问题规模的时间函数 ,n:代表的是问题的规模 输入数据量的大小
举例: 对一个int a[100];进行冒泡排序 100 == n
O :时间数量级
f(n) :算法中可执语句重复执行的次数 ,用问题规模n的某个函数f(n)来表达
例1:
求 1 + 2 + 3 + 4 + ....... n 的和
- 算法一
int sum = 0; n = 100 100次
int i;
for(i = 1; i <= n; i++) n = 1000 1000次
{
sum += i;
} f(n) = n;
T(n) = O(n);
- 算法二
int sum = n*(n+1)/2 n = 100 1 次
n = 1000 1次
f(n) = 1;
T(n) = O(1);
例2:
int i,j;
for(i = 0; i < n; i++)//外循环循环一次,内循环跑一圈 n
{
for(j = 0; j < n; j++)// n
{
printf("hello world!! "); // n * n
}
}
f(n) = n*n;
T(n) = O(n^2);
例3
int i,j;
for(i = 0; i < n; i++)//外循环循环一次,内循环跑一圈 n
{
for(j = 0; j <= i; j++)//内循环的次数与i的值相关
{
printf("hello world!! ");
}
}
i的值 循环次数
i == 0 1
i == 1 2
i == 2 3
...
...
i == n-2 n-1
i == n-1 n
循环次数 = 1 + 2 + 3 + 4 + ..... + n
f(n) = n*(n+1)/2
f(n) = n^2/2 + n/2
//最高项n^2 ,只保留最高项,其它项舍去 f(n) = n^2/2 ,再除以最高项系数 除以1/2 f(n) = n^2
//经过处理之后 :T(n) = O(n^2)
计算大O的方法
1、根据问题规模n写出表达式 f(n)
2、如果有常数项,将其置为1 n^0 *8 。//当f(n)的表达式中只有常数项的时候,有意义 f(n) = 8
3、只保留最高项,其它项舍去
4、如果最高项系数不为1,除以最高项系数
f(n) = 3*n^5 + 2*n^3 + 6*n + 10 //10 代表的是常数项;//3* 2* 6* 系数项
//最高项指的是指数 ^5 ^3 ^1 最高项为 n^5
T(n) = O(n^5)
f(n) = n^0 *8;//最高项 n^0
T(n) = O(1);
二、线性表
线性表:顺序表 链表(单向链表 双向链表 单向循环链表 双向循环链表) 栈 队列
1、逻辑结构:线性结构
2、存储结构:
1)顺序存储 --->数组
2)链式存储 --->链表
3、线性表的特点
一对一,每个节点最多一个前驱和一个后继
首尾节点特殊:首节点无前驱,尾节点无后继
(一) 顺序表(sequence list)
1、顺序表前言
逻辑结构:线性结构
存储结构:顺序存储结构 在内存当中存储是连续的 (数组)。
顺序表特点:
1、顺序表在内存当中是连续存储的
2、顺序表的长度是固定 #define N 5
3、顺序表查找数据的时候方便的,插入和删除麻烦
命名法则:
大驼峰:InsertInto
小驼峰: insertinto
加下划线: insert_into
见名知意;
练习(模块化):
(1)向数组的第几个位置插入数据
(2)遍历数组中的有效元素
方法一:
#include <stdio.h>
void show(int *p,int n);
int InsertInto(int *p,int n,int post,int data);
int main(int argc, const char *argv[])
{
int arr[32]={1,2,3,4,5,6,7,8,9};
show(arr,9);
InsertInto(arr,9,3,10);
show(arr,10);
return 0;
}
void show(int *p,int n)
{
int i;
for (int i=0;i<n;i++)
{
printf("arr[%d]=%d
",i,p[i]);
}
putchar(10);
}
int InsertInto(int *p,int n,int post,int data)
{
if (post<0||post>n)
{
printf("InserInto erro");
return -1;
}
for (int i=n-1;i>=post;i--){
p[i+1]=p[i];
}
p[post]=data;
return 0;
}
InsertInt函数代码中传入的参数解释如下
int *p :保存的数组的首地址
int n :n代表的是数组中有效的元素个数(非数组的长度size 100)
int post:位置代表的是第几个位置,数组元素下标 位置的编号从0开始 position
int data:插入到数组中的数据
方法2:
修改成last版本
全局变量:last :始终表示最后一个有效元素的下标
#include <stdio.h>
void show(int *p,int n);
int InsertInto(int *p,int post,int data);
int last=9; //始终代表最后一个元素的下标
int main(int argc, const char *argv[])
{
int arr[32]={1,2,3,4,5,6,7,8,9};
show(arr,9);
InsertInto(arr,3,10);
show(arr,10);
return 0;
}
void show(int *p,int n)
{
int i;
for (int i=0;i<n;i++)
{
printf("arr[%d]=%d
",i,p[i]);
}
putchar(10);
}
int InsertInto(int *p,int post,int data)
{
if (post<0||post>last+1)
{
printf("InserInto erro");
return -1;
}
for (int i=last;i>=post;i--){
p[i+1]=p[i];
}
p[post]=data;
last++; //始终代表最后一个元素的下标,插入元素后,需要加一
return 0;
}
2、顺序表的操作
(1)创建一个空的顺序表
seqlist_t *CreateEpSeqlist();//返回的是申请空间的首地址
(2)向顺序表的指定位置插入数据
int InsertIntoSeqlist(seqlist_t *p, int post,int data);//post第几个位置,data插入的数据
(3)遍历顺序表
void ShowSeqlist(seqlist_t *p);
(4)判断顺序表是否为满,满返回1 未满返回0
int IsFullSeqlist(seqlist_t *p);
(5)判断顺序表是否为空
int IsEpSeqlist(seqlist_t *p);
(6)删除顺序表中指定位置的数据
post删除位置
int DeletePostSeqlist(seqlist_t *p, int post);
(7)清空顺序表
void ClearSeqList(seqlist_t *p)
(8)修改指定位置的数据
int ChangePostSeqList(seqlist_t *p,int post,int data);//post被修改的位置,data修改成的数据
(9)查找指定数据出现的位置
int SearchDataSeqList(seqlist_t *p,int data);//data代表被查找的数据
实现:
seqlist.h文件如下:
#ifndef __SEQLIST_H__
#define __SEQLIST_H__
#define N 10
#include <stdio.h>
#include <stdlib.h>
typedef struct list_t
{
int data[N];
int last;
}seqlist_t;
seqlist_t *CreateEpseqlist(void);
void ShowSeqlist(seqlist_t *p);
int InsertIntoSeqlist(seqlist_t *p,int post,int data);
int isfullseqlist(seqlist_t *p);
int isEPseqlist(seqlist_t *p);
int DeletePostSeqlist(seqlist_t *p,int post);
void Clearseqlist(seqlist_t *p);
int ChangePostSeqlist(seqlist_t *p,int post,int data);
int SearchPostSeqlist(seqlist_t *p,int data);
#endif
seqlist.c文件如下:
#include "seqlist.h"
//开辟空间
seqlist_t *CreateEpseqlist(void) //返回的是申请空间的首地址
{
seqlist_t *p=(seqlist_t *)malloc(sizeof(seqlist_t));
if(NULL==p)
{
printf("error
");
return NULL;
}
p->last=-1; //last 始终代表数组中最后一个有效元素的下标
return p;
}
//向顺序表的指定位置插入数据
int InsertIntoSeqlist(seqlist_t *p,int post,int data)
{
if (post<0||post>p->last+1||isfullseqlist(p))
{
printf("InserInto erro");
return -1;
}
int i;
for (i=p->last;i>=post;i--)
{
p->data[i+1]=p->data[i];
}
p->data[post]=data;
p->last++;
return 0;
}
//遍历顺序表
void ShowSeqlist(seqlist_t *p)
{
int i;
for (i=0;i<=p->last;i++)
{
printf("arr[%d]=%d
",i,p->data[i]);
}
}
//判断顺序表是否为满,满返回1,未满返回0
int isfullseqlist(seqlist_t *p)
{
return p->last==N-1;
}
//判断顺序表是否为空
int isEPseqlist(seqlist_t *p)
{
return p->last==-1;
}
//删除顺序表中指定位置的数据
int DeletePostSeqlist(seqlist_t *p,int post)
{
if (post<0||post>p->last||isEPseqlist(p))
{
printf("DeletePostSeqlist erro");
return -1;
}
int i;
for (i=post+1;i<=p->last;i++){
p->data[i-1]=p->data[i];
}
p->last--;
return 0;
}
//清空顺序表
void Clearseqlist(seqlist_t *p)
{
p->last=-1;
}
//修改指定位置的数据
int ChangePostSeqlist(seqlist_t *p,int post,int data)
{
if (post<0||post>p->last+1||isEPseqlist(p))
{
printf("DeletePostSeqlist erro");
return -1;
}
p->data[post]=data;
return 0;
}
//查找指定数据出现的位置
int SearchPostSeqlist(seqlist_t *p,int data)
{
if (isEPseqlist(p))
{
printf("SearchPostSeqlist erro");
return -1;
}
for(int i=0;i<p->last;i++)
{
if(p->data[i]==data)
return i;
}
return -1;
}
main.c文件如下:
#include "seqlist.h"
int main(int argc, const char *argv[])
{
seqlist_t *p=CreateEpseqlist();
InsertIntoSeqlist(p,0,1);
InsertIntoSeqlist(p,1,2);
InsertIntoSeqlist(p,2,3);
ShowSeqlist(p);
putchar(10);
#if 1
InsertIntoSeqlist(p,1,6);
ShowSeqlist(p);
putchar(10);
#endif
#if 1
DeletePostSeqlist(p,3);
ShowSeqlist(p);
putchar(10);
#endif
#if 1
ChangePostSeqlist(p,1,8);
ShowSeqlist(p);
putchar(10);
#endif
#if 1
printf("seach in data[%d]",SearchPostSeqlist(p,8));
putchar(10);
#endif
#if 1
printf("%d
",isfullseqlist(p));
putchar(10);
#endif
#if 1
printf("%d
",isEPseqlist(p));
putchar(10);
#endif
#if 1
Clearseqlist(p);
free (p);
p=NULL;
#endif
return 0;
}
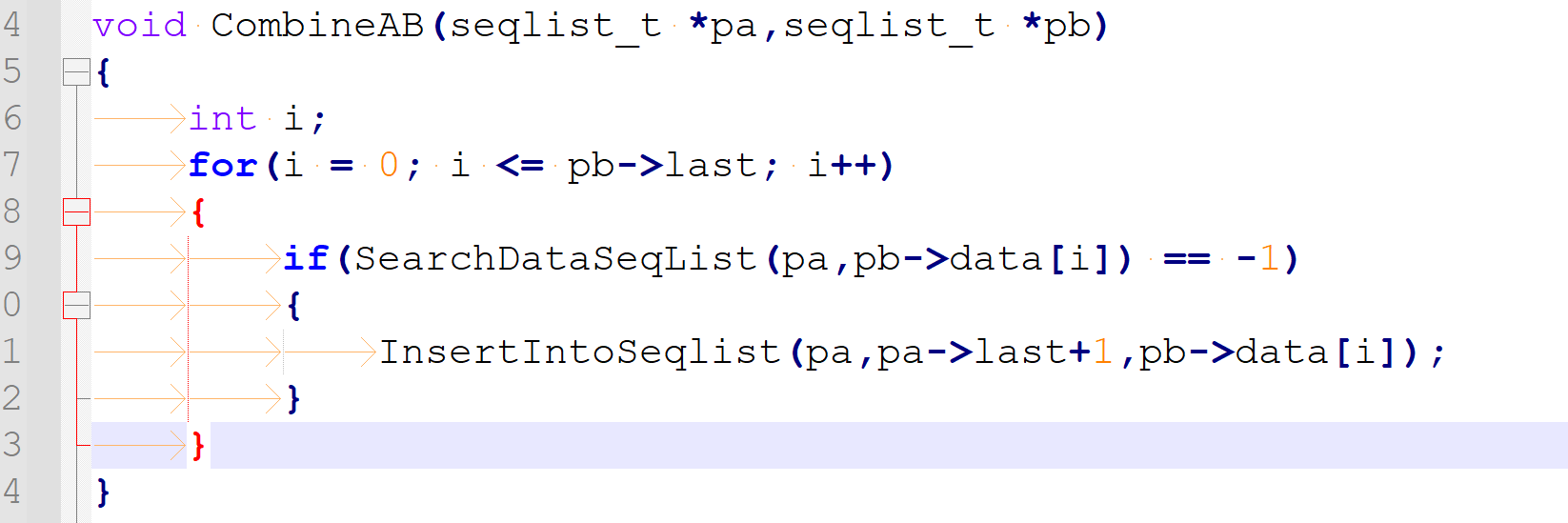
3、练习:求AUB
集合A: 1 3 5 7 //顺序表A
集合B:5 7 9 11 //顺序表B
求AUB:1 3 5 7 9 11
void Compare(seqlist_t *pa,seqlist_t *pb,seqlist_t *pc)
{
int i=0,j=0,k=0;
while(i<=pa->last&&j<=pb->last)
{
if(pa->data[i]<pb->data[j])
{
pc->data[k]=pa->data[i];
k++;
i++;
pc->last++;
}else if(pa->data[i]==pb->data[j]){
pc->data[k]=pa->data[i];
k++;
i++;
j++;
pc->last++;
}
else
{
pc->data[k]=pb->data[j];
k++;
j++;
pc->last++;
}
}
while(i<=pa->last){
pc->data[k]=pa->data[i];
k++;
i++;
pc->last++;
}
while(j<=pb->last){
pc->data[k]=pb->data[j];
k++;
j++;
pc->last++;
}
}
(二)链表
1、链表前言
单向链表 单向循环链表 双向链表 双向循环链表
解决:长度固定的问题,插入和删除麻烦的问题
1、逻辑结构: 线性结构
2、存储结构: 链式存储
3、操作: 增 删 改 查
typedef struct node_t
{
char data; //数据域
struct node_t *next; //指针域 ,指针指向自身结构体的类型(存放的下一个节点的地址)
}link_node_t,* link_list_t; //结构体数据类型,结构体指针类型
struct node_t《-》link_node_t
struct node_t * 《-》link_list_t《-》link_node_t *
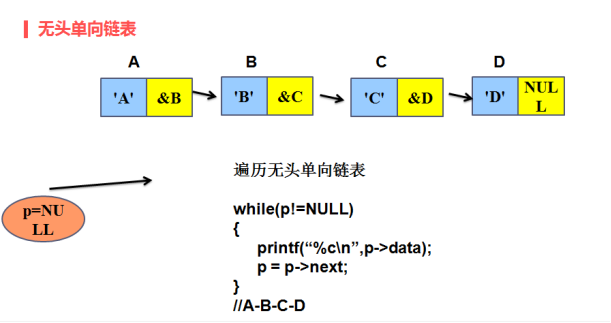
2、遍历有头无头单向链表
(1)遍历无头的单向链表
链表中的每一个节点的数据域和指针域都是有效的
#include <stdio.h>
typedef struct node_t
{
char data;
struct node_t *next;
}link_node_t,*link_list_t;
int main(int argc, const char *argv[])
{
link_node_t a={
.data='a',
.next=NULL,
};
link_node_t b={
.data='b',
.next=NULL,
};
link_node_t c={
.data='c',
.next=NULL,
};
link_node_t d={'d',NULL};
link_node_t e={'e',NULL};
link_node_t f={'f',NULL};
link_list_t p=&a;
a.next=&b;
b.next=&c;
c.next=&d;
d.next=&e;
e.next=&f;
while(p!=NULL){
printf("%c
",p->data);
p=p->next;
}
return 0;
}
(2)遍历有头的单向链表
链表中的第一个头节点的数据域无效,但指针域有效

#include <stdio.h>
typedef struct node_t
{
char data;
struct node_t *next;
}link_node_t,*link_list_t;
int main(int argc, const char *argv[])
{
link_node_t head={
.next=NULL,
};
link_node_t a={
.data='a',
.next=NULL,
};
link_node_t b={
.data='b',
.next=NULL,
};
link_node_t c={
.data='c',
.next=NULL,
};
link_node_t d={'d',NULL};
link_node_t e={'e',NULL};
link_node_t f={'f',NULL};
link_list_t p=&head;
head.next=&a;
a.next=&b;
b.next=&c;
c.next=&d;
d.next=&e;
e.next=&f;
while(p->next!=NULL){
p=p->next;
printf("%c
",p->data);
}
return 0;
}
3、有头单向链表操作思想
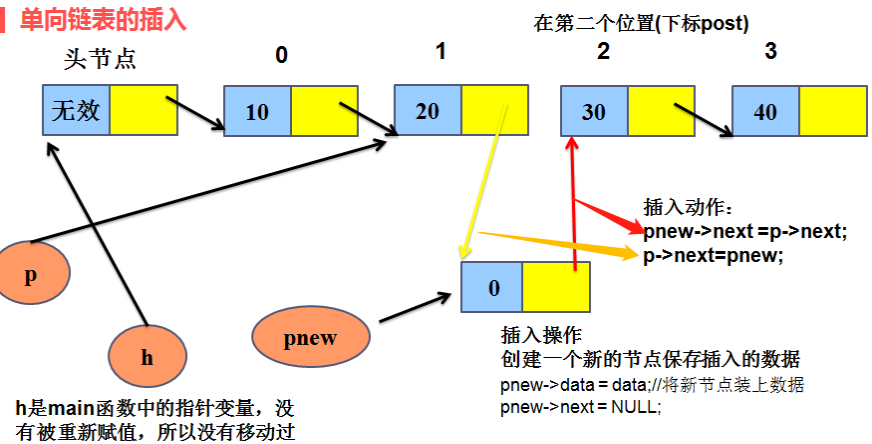
(1)链表插入:
解题思想:
1、先遍历找到要插入节点的前一个节点,假设这个节点为A;A的下一个节点为B;
将C插入A与B之间;
2、先让C的指针域指向B;
3、再让A的指针域指向C;
(注意:顺序不可以调换)
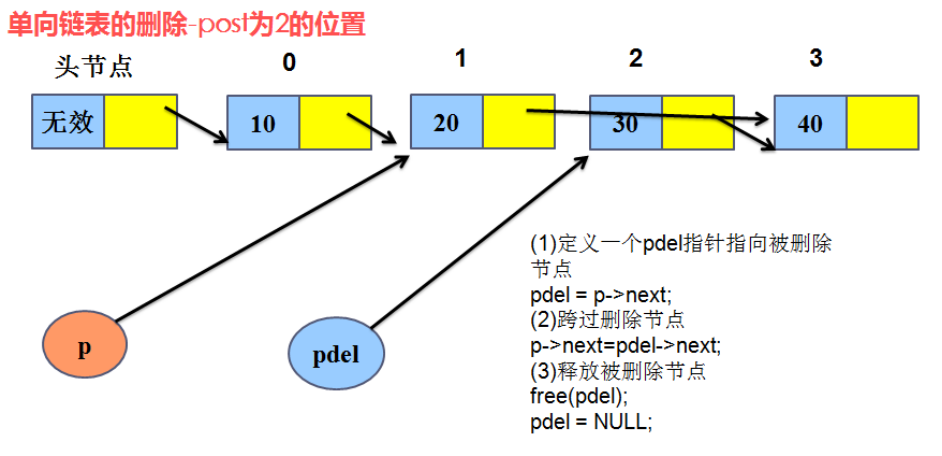
(2)链表删除:
解题思想:
1、先遍历找到要删除节点的前一个节点,假设为A;
2、找一个临时指针指向要删除的节点;
3、将A的指针域指向删除节点的下一个节点;
(3)转置链表
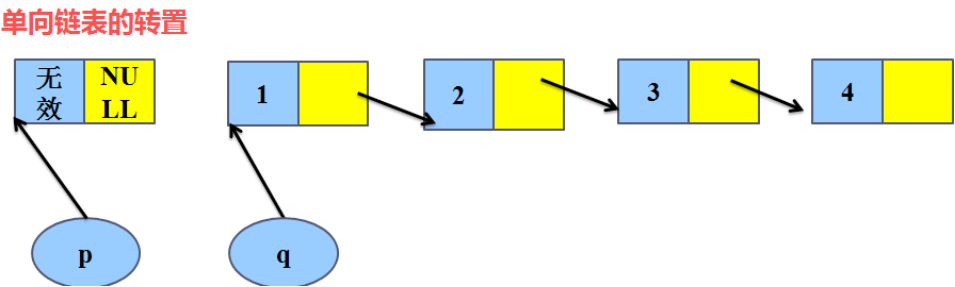
解题思想:
1、将头节点与当前链表断开,断开前保存头节点的下一个节点,保证后面链表能找得到,定义一个q保存头节点的下一个节点,断开后前面相当于一个空的链表,后面是一个无头的单向链表
2、遍历无头链表的所有节点,将每一个节点当做新节点插入空链表头节点的下一个节点(每次插入的头节点的下一个节点位置)
void ReverseLinkList(link_node_t *p)
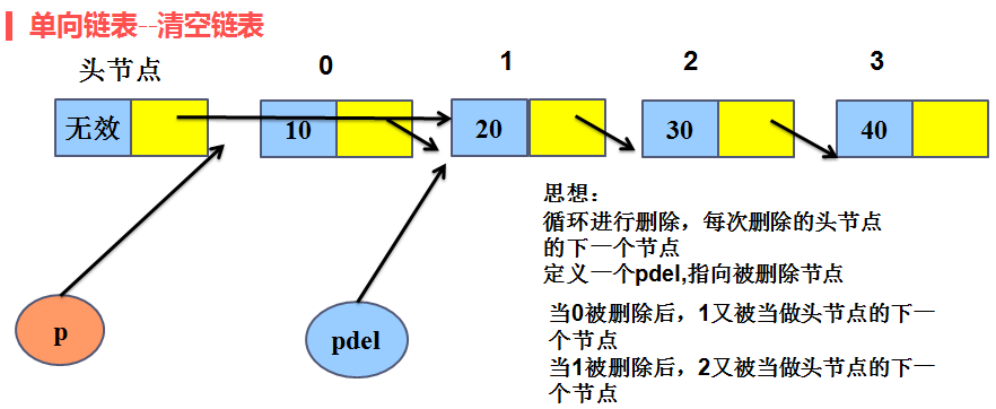
(4)链表清空:
4、单链表的实现函数
1.创建一个空的单向链表(有头单向链表)
link_node_t *CreateEpLinkList();
2.向单向链表的指定位置插入数据
p保存链表的头指针 post 插入的位置 data插入的数据
int InsertIntoPostLinkList(link_node_t *p,int post, datatype data);
3.遍历单向链表
void ShowLinkList(link_node_t *p);
4.求单向链表长度的函数
int LengthLinkList(link_node_t *p);
5.删除单向链表中指定位置的数据 post 代表的是删除的位置
int DeletePostLinkList(link_node_t *p, int post);
6.判断单向链表是否为空 1代表空 0代表非空
int IsEpLinkList(link_node_t *p);
7.修改指定位置的数据 post 被修改的位置 data修改成的数据
int ChangePostLinkList(link_node_t *p, int post, datatype data);
8.查找指定数据出现的位置 data被查找的数据 //search 查找
int SearchDataLinkList(link_node_t *p, datatype data);
9.转置链表
void ReverseLinkList(link_node_t *p);
10.删除单向链表中出现的指定数据,data代表将单向链表中出现的所有data数据删除
int DeleteDataLinkList(link_node_t *p, datatype data);
11.清空单向链表
void ClearLinkList(link_node_t *p);
linklist.h文件:
#ifndef __LINKLIST__H_
#define __LINKLIST__H_
#include <stdio.h>
#include <stdlib.h>
typedef int datatype;
typedef struct node_t
{
datatype data;
struct node_t *next;
}link_node_t,*link_list_t;
link_list_t CreateEplist();
int InsertIntoPostLinkList(link_list_t p,int post,datatype data);
void ShowLinkList(link_list_t p);
int LengthLinkList(link_list_t p);
int DeleteLinkList(link_list_t p,int post);
int IsEpLinkList(link_list_t p);
int ChangePostLinkList(link_list_t p,int post,datatype data);
int SearchDataLinkList(link_list_t p,datatype data);
void ReverseLinkList(link_list_t p);
void ClearLinkList(link_list_t p);
int DeleteDataLinkList(link_list_t p,int data);
#endif
linklist.c文件:
#include "linklist.h"
//创建一个空的单向链表(有头单向链表)
link_list_t CreateEplist()
{
link_list_t h=(link_list_t)malloc(sizeof(link_node_t));
if(NULL==h)
{
printf("error");
return NULL;
}
h->next=NULL;
return h;
}
//向单链表的指定位置插入数据
int InsertIntoPostLinkList(link_list_t p,int post,datatype data) /
{
if(post<0||post>LengthLinkList(p))
{
printf("erro
");
return -1;
}
link_list_t pnew=(link_list_t)malloc(sizeof(link_node_t));
if(NULL==pnew)
{
printf("error");
return -1;
}
pnew->data=data;
pnew->next=NULL;
for(int i=0;i<post;i++)
{
p=p->next;
}
pnew->next=p->next;
p->next=pnew;
return 0;
}
//遍历单向链表
void ShowLinkList(link_list_t p)
{
if(p->next==NULL)
{
printf("empt LinkList
");
}
while(p->next!=NULL)
{
p=p->next;
printf("%d",p->data);
putchar(10);
}
}
//求单链表长度的函数
int LengthLinkList(link_list_t p)
{
int lenth=0;
while(p->next!=NULL)
{
p=p->next;
lenth++;
}
return lenth;
}
//删除单链表中指定位置的数据
int DeleteLinkList(link_list_t p,int post)
{
if(post<0||post>=LengthLinkList(p)||IsEpLinkList(p))
{
printf("erro
");
return -1;
}
for(int i=0;i<post;i++)
{
p=p->next;
}
link_list_t pdel=p->next;
p->next=pdel->next;
free(pdel);
pdel=NULL;
return 0;
}
//判断单链表是否为空,1代表空,0代表非空
int IsEpLinkList(link_list_t p)
{
return p->next==NULL;
}
// 修改指定位置上的数据
int ChangePostLinkList(link_list_t p,int post,datatype data)
{
if(post<0||post>=LengthLinkList(p)||IsEpLinkList(p))
{
printf("erro
");
return -1;
}
for(int i=0;i<=post;i++)
{
p=p->next;
}
p->data=data;
return 0;
}
//查找指定数据出现的数据
int SearchDataLinkList(link_list_t p,datatype data)
{
if(IsEpLinkList(p))
{
printf("error
");
return -1;
}
int i=0;
while(p->next!=NULL){
p=p->next;
if(p->data==data)
{
return i;
}
i++;
}
return -1;
}
//转置链表
void ReverseLinkList(link_list_t p)
{
link_list_t q=p->next;
link_list_t temp=NULL;
p->next=NULL;
while(q!=NULL)
{
temp=q->next;
q->next=p->next;
p->next=q;
q=temp;
}
}
//清空单向链表
void ClearLinkList(link_list_t p)
{
link_list_t pdel=NULL;
while(p->next!=NULL)
{
pdel=p->next;
p->next=pdel->next;
free(pdel);
pdel=NULL;
}
}
//删除单向链表中出现的指定数据
int DeleteDataLinkList(link_list_t p,int data)
{
if(IsEpLinkList(p))
{
printf("erro
");
return -1;
}
link_list_t pdel=NULL;
while(p->next!=NULL)
if(p->next->data==data)
{
pdel=p->next;
p->next=pdel->next;
free(pdel);
pdel=NULL;
}
else{
p=p->next;
}
return 0;
}
main.c文件:
#include "linklist.h"
int main(int argc, const char *argv[])
{
link_list_t p=CreateEplist();
#if 1
InsertIntoPostLinkList(p,0,1);
InsertIntoPostLinkList(p,1,2);
InsertIntoPostLinkList(p,2,3);
InsertIntoPostLinkList(p,3,4);
ShowLinkList(p);
putchar(10);
#endif
DeleteLinkList(p,0);
ShowLinkList(p);
putchar(10);
ChangePostLinkList(p,1,5);
ShowLinkList(p);
putchar(10);
printf("%d
",SearchDataLinkList(p,5));
putchar(10);
ReverseLinkList(p);
ShowLinkList(p);
putchar(10);
DeleteDataLinkList(p,5);
ShowLinkList(p);
putchar(10);
ClearLinkList(p);
free(p);
p=NULL;
ShowLinkList(p);
return 0;
}
练习1:
向一个单链表linklist中的节点t后面插入一个节点p,下列操作正确的是( )
a)p->next = t->next;t->next = p;
b)t->next = p->next;t->next = p;
c)t->next = p;p->next = t->next;
d)t->next = p;t->next = p->next;
5、单向循环链表 解决约瑟夫问题
约瑟夫问题
约瑟夫问题为:设编号为1,2,……n得n个人围坐一圈,约定编号为k(k大于等于1并且小于等于n)的人从1开始报数,数到m的那个人出列。它的下一位继续从1开始报数,数到m的人出列,依次类推,最后剩下一个为猴王。
根据下图展示,初始化状态:假设n=6,总共有6个人,k=1,从第一个人开始报数,m=5,每次数五个。
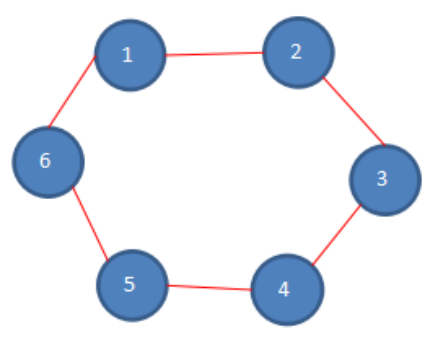
第一次报数:从一号开始,数五个数,1-2-3-4-5,数完五个数,五号被杀死,第一次报数后,剩余人数如下。
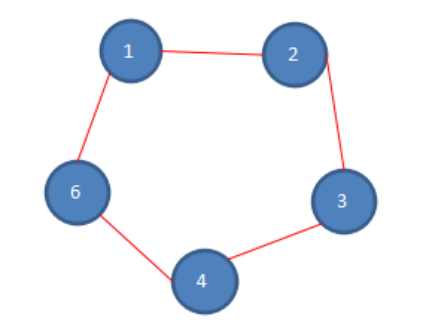
第二次报数:从被杀死的五号的下一位开始报数,也就是六号,数五个数,6-1-2-3-4,数数完毕,四号被杀死,第二次报数后,剩余人数如下。
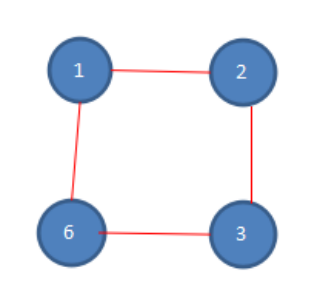
第三次报数:从被杀死的四号的下一位开始报数,同样是六号,数五个数,6-1-2-3-6,数数完毕,六号被杀死,第三次报数后,剩余人数如下。
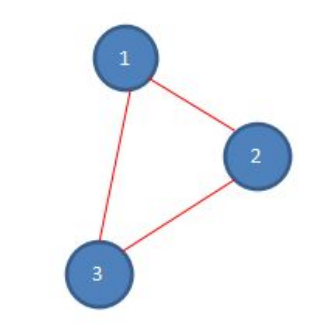
第四次报数:从被杀死的六号的下一位开始报数,也就是一号,数五个数,1-2-3-1-2,数数完毕,二号被杀死,第四次报数后,剩余人数如下。
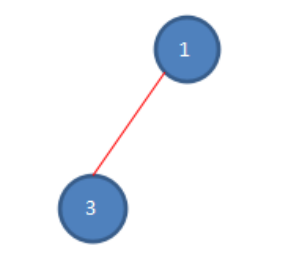
第五次报数:从被杀死的二号的下一位开始报数,也就是三号,数五个数,3-1-3-1-3,数数完毕,三号被杀死,只剩下一号

#include <stdio.h>
#include <stdlib.h>
typedef struct node_t
{
int data;
struct node_t *next;
}link_node_t,*link_list_t;
int main(int argc, const char *argv[])
{
link_list_t h=NULL; //用于指向头结点
link_list_t pdel=NULL; //用于指向被删除节点
link_list_t ptail=NULL; //用于指向当前链表的尾
link_list_t pnew=NULL; //用于指向新创建的节点
int kill_num; //数到几淘汰猴子
int start_num; //从几号猴子开始
int all_sum; //总数
printf("please input monkey all_sum:");
scanf("%d",&all_sum);
printf("please input start_num:");
scanf("%d",&start_num);
printf("please input monkey kill_num:");
scanf("%d",&kill_num);
h=(link_list_t)malloc(sizeof(link_node_t));
if(h==NULL)
{
printf("error");
return -1;
}
h->data=1;
h->next=NULL;
ptail=h; //尾指针指向当前第一个节点
for(int i=2;i<=all_sum;i++)
{
pnew=(link_list_t)malloc(sizeof(link_node_t));
if(pnew==NULL) //创建新节点
{
printf("error");
return -1;
}
pnew->data=i; //为新节点赋值
pnew->next=NULL;
ptail->next=pnew; //将新节点连接到链表尾部
ptail=pnew; //尾指针跟随移动到尾部
}
ptail->next=h; //将头指针保存到链表尾部,形成单向循环链表
//开始淘汰猴子
for(int i=0;i<start_num-1;i++) //将头指针移动到开始的猴子号码处
h=h->next;
//循环进行淘汰猴子
while(h!=h->next) //条件不成的时候,就剩一个猴子,只有一个节点
{
for(int i=0;i<kill_num-2;i++) //将头指针移动到即将删除节点的前一个节点
h=h->next;
pdel=h->next;
h->next=pdel->next; //跨过删除节点
printf("kill %d
",pdel->data); //打印被淘汰的猴子
free(pdel);
pdel=NULL;
h=h->next; //淘汰该猴子后,从下一个节点开始继续开始数,将头指针移动到开始数的地方
}
printf("king is %d
",h->data); //国王诞生
return 0;
}
6、总结:顺序表和单向链表比较(****)
1、顺序表在内存当中连续存储的(数组),但是链表在内存当中是不连续存储的,通过指针将数据链接在一起
2、顺序表的长度是固定的,但是链表长度不固定
3、顺序表查找方便(下标),但是插入和删除麻烦(post~last),链表,插入和删除方便,查找麻烦
(为什么操作麻烦,为什么操作方便?)
作业
1、把今天的代码敲三遍
2、
递增有序的链表A 1 3 5 7 9 10
递增有序的链表B 2 4 5 8 11 15
新链表:1 2 3 4 5 5 7 8 9 10 11 15
将链表A和B合并,形成一个递增有序的新链表

(三)栈
1、前言
(1)什么是栈?
只能在一端进行插入和删除操作的线性表(又称为堆栈),进行插入和删除操作的一端称为栈顶,另一端称为栈底
(2)栈特点:
先进后出 FILO first in last out
杯子:往杯子里放大饼,先放进去的大饼,最后一个拿出来
2、顺序栈(sequence stack)
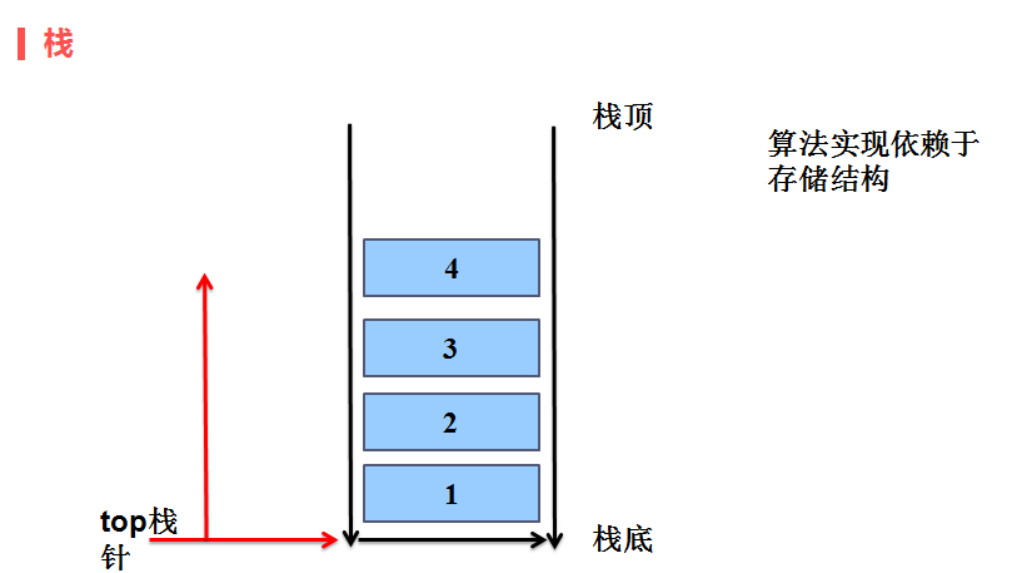
1. 逻辑结构: 线性结构
2. 存储结构: 顺序存储 (用数组的思想来实现
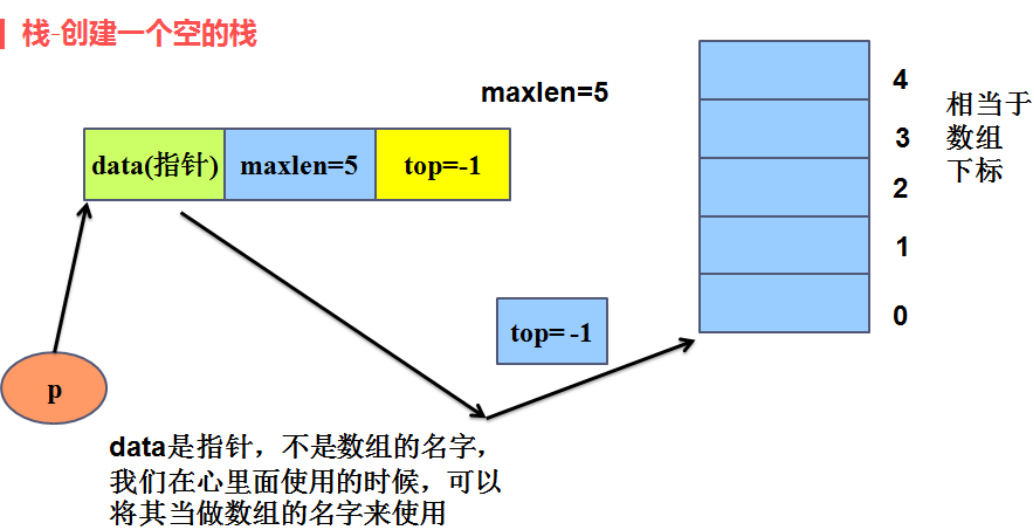
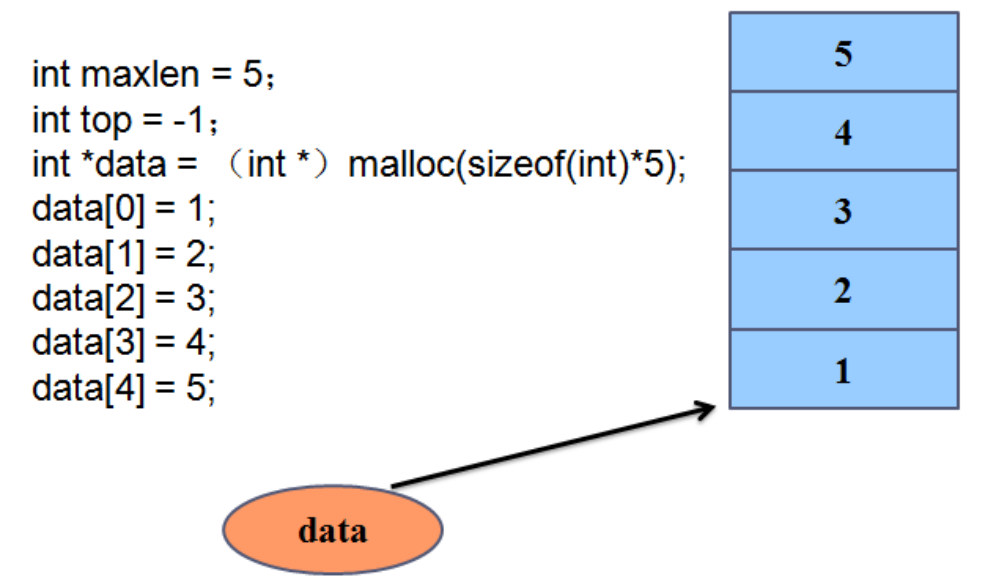
seqstack.h文件:
#ifndef _SEQSTACK_H_
#define _SEQSTACK_H_
#include <stdio.h>
#include <stdlib.h>
typedef struct seqstack
{
int *data; //指向栈的存储位置
int maxlen; //保存栈的最大长度
int top; //栈针,心里可以认为是顺序表中的last,始终代表最后一个有效元素的下标
}seqstack_t;
seqstack_t *CreateEPSeqStack(int len);
int IsEpseqstack(seqstack_t *p);
int IsFullSeqStack(seqstack_t *p);
int PushStack(seqstack_t *p,int data);
int IsEpseqstack(seqstack_t *p);
int PopSeqStack(seqstack_t *p);
void ClearSeqStack(seqstack_t *p);
int GetTopSeqStack(seqstack_t *p);
int LenthSeqStack(seqstack_t *p);
#endif
seqstack.c文件:
#include "seqstack.h"
//1、创建一个空的栈
seqstack_t *CreateEPSeqStack(int len) //len代表的是创建栈的时候的最大长度
{
seqstack_t *p=(seqstack_t *)malloc(sizeof(seqstack_t));
if(NULL==p)
{
printf("malloc error");
return NULL;
}
//给p指向的成员初始化
p->maxlen=len;
p->top=-1;
//申请存放数据的存储空间
p->data=(int *)malloc(sizeof(int) *len);
if(NULL==p->data)
{
printf("malloc error");
return NULL;
}
return p;
}
//2、判断是否为满,满的话返回1,未满返回0
int IsFullSeqStack(seqstack_t *p)
{
return p->top==p->maxlen-1;
}
// 3、入栈
int PushStack(seqstack_t *p,int data)
{
if(IsFullSeqStack(p))
{
printf("push error");
return -1;
}
p->top++;
p->data[p->top]=data;
return 0;
}
//4、判断是否为空
int IsEpseqstack(seqstack_t *p)
{
return p->top==-1;
}
//5、出栈
int PopSeqStack(seqstack_t *p)
{
if(IsEpseqstack(p))
{
printf("pop error");
return -1;
}
p->top--;
return p->data[p->top+1];
}
//6、清空栈
void ClearSeqStack(seqstack_t *p)
{
p->top=-1;
}
//7、获取栈顶元素
int GetTopSeqStack(seqstack_t *p)
{
return p->data[p->top];
}
//8、求栈内有效元素的长度
int LenthSeqStack(seqstack_t *p)
{
return p->top+1;
}
main.c文件:
#include "seqstack.h"
int main(int argc, const char *argv[])
{
seqstack_t *p=CreateEPSeqStack(10);
int i;
for(i=0;i<5;i++)
{
PushStack(p,i);
}
printf("lenth:%d
",LenthSeqStack(p));
for(i=0;i<5;i++)
{
printf("data:%d
",PopSeqStack(p));
}
return 0;
}
3、链式栈(link stack)
(1)逻辑结构: 线性结构
(2)存储结构: 链式存储
(3)顺序栈和链式栈的区别是 实现的方式不同,链栈用链表
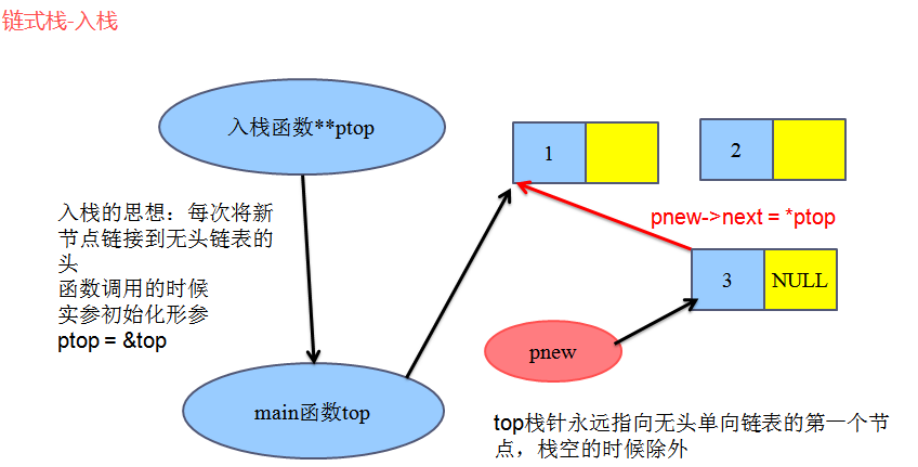
(4)栈的操作:使用无头单向链表
入栈:
出栈:
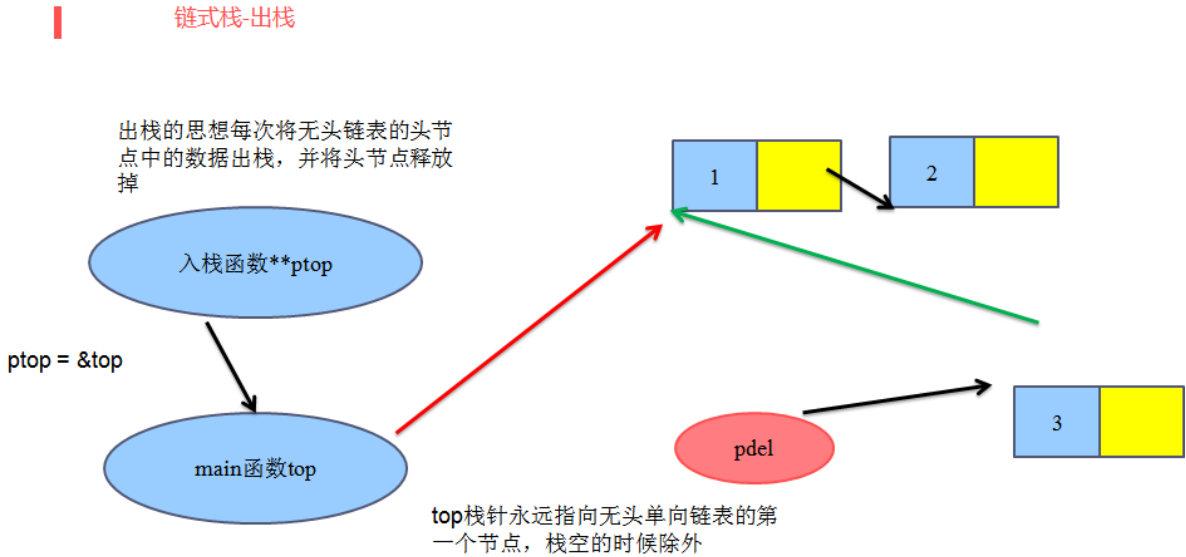
Last;top;->结构类型里面的成员
1:一端进行插入和删除(先进后出)
2:标记;始终指向栈顶(指针类型)
入栈、出栈(top:栈指针(始终指向栈顶))
linklist.h文件
#ifndef _LINKSTACK_H_
#define _LINKSTACK_H_
#include <stdio.h>
#include <stdlib.h>
//入栈和出栈只在第一个节点位置操作
typedef int datatype;
typedef struct linkstack
{
datatype data; //数据域
struct linkstack *next;//指针域
}linkstack_t;
void CreateEPLinkStack(linkstack_t **ptop);
int PushLinkStack(linkstack_t **ptop,datatype data);
int IsEpLinkStack(linkstack_t *ptop);
int PopLinkStack(linkstack_t **ptop);
void ClearLinkStack(linkstack_t **ptop);
int LengthListStack(linkstack_t *top);
datatype GetTopLinkStack(linkstack_t *top);
#endif
linklist.c文件
#include "linkstack.h"
//1、创建一个空的栈
void CreateEPLinkStack(linkstack_t **ptop)
{
*ptop=NULL;
}
//2、入栈
/*参数上之所以采用二级指针,因为我们要随着入栈添加新的节点作为头,
top需要永远指向当前链表的头,那么修改main函数中的top,我们采用地址传递 */
int PushLinkStack(linkstack_t **ptop,datatype data)
{
linkstack_t *pnew=(linkstack_t *)malloc(sizeof(linkstack_t));
if (pnew==NULL)
{
printf("malloc error");
return -1;
}
//新节点初始化
pnew->data=data;
pnew->next=NULL;
//新节点放到栈顶位置
pnew->next=*ptop;
*ptop=pnew;
return 0;
}
//3、判断是否为空
int IsEpLinkStack(linkstack_t *top)
{
return top==NULL;
}
//4、出栈
int PopLinkStack(linkstack_t **ptop)
{
if(IsEpLinkStack(*ptop))
{
printf("pop error");
return -1;
}
int temp;
linkstack_t *pdel=NULL;
//出栈顶数据
pdel=*ptop;
//出栈一个元素后栈顶指针需要指向新的栈顶节点
*ptop=pdel->next;
temp=pdel->data;
free(pdel);
pdel=NULL;
return temp;
}
//5、清空栈
void ClearLinkStack(linkstack_t **ptop)
{
while(!IsEpLinkStack(*ptop))
{
PopLinkStack(ptop);
}
}
//6、求栈的长度
int LengthListStack(linkstack_t *top)
{
int len=0;
while(top!=NULL)
{
len++;
top=top->next;
}
return len;
}
//7、获取栈顶数据
datatype GetTopLinkStack(linkstack_t *top)
{
if(!IsEpLinkStack(top))
{
return top->data;
}
return -1;
}
main.c文件
#include "linkstack.h"
int main(int argc, const char *argv[])
{
linkstack_t *top;
CreateEPLinkStack(&top);
int i;
for(i=0;i<5;i++)
{
PushLinkStack(&top,i);
}
printf("lenth:%d
",LengthListStack(top));
printf("topdata:%d
",GetTopLinkStack(top));
ClearLinkStack(&top);
printf("lenth:%d
",LengthListStack(top));
for(i=0;i<5;i++)
{
printf("%d
",PopLinkStack(&top));
}
return 0;
}
总结:
顺序栈和链式栈的区别是什么?
(1)存储结构不同,顺序栈相当于数组,连续的,链式栈 链表非连续的
(2)顺序栈的长度受限制,而链栈不会
2、写一个子函数(12),将其转换为二进制数,将所有二进制位存储到栈内,之后再出栈打印输出
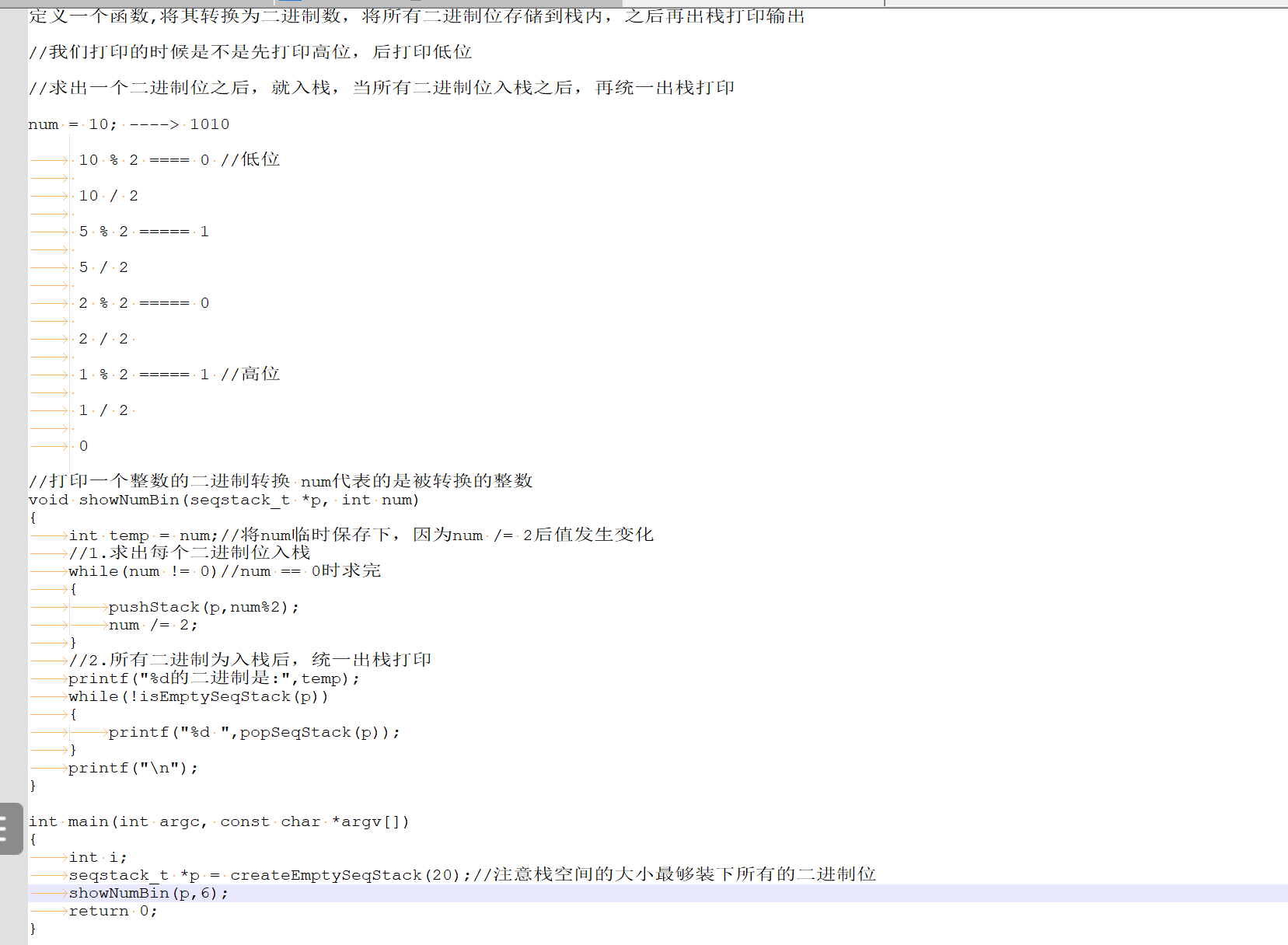
(四)队列
1、队列前言
线性表的特征是什么?
线性表:顺序表、链表、栈(顺序栈和链式栈)、 队列(顺序队列也叫循环队列和链式队列)
线性表的特征:一对一,每个节点最多有一个前驱和一个后继(首尾节点除外)
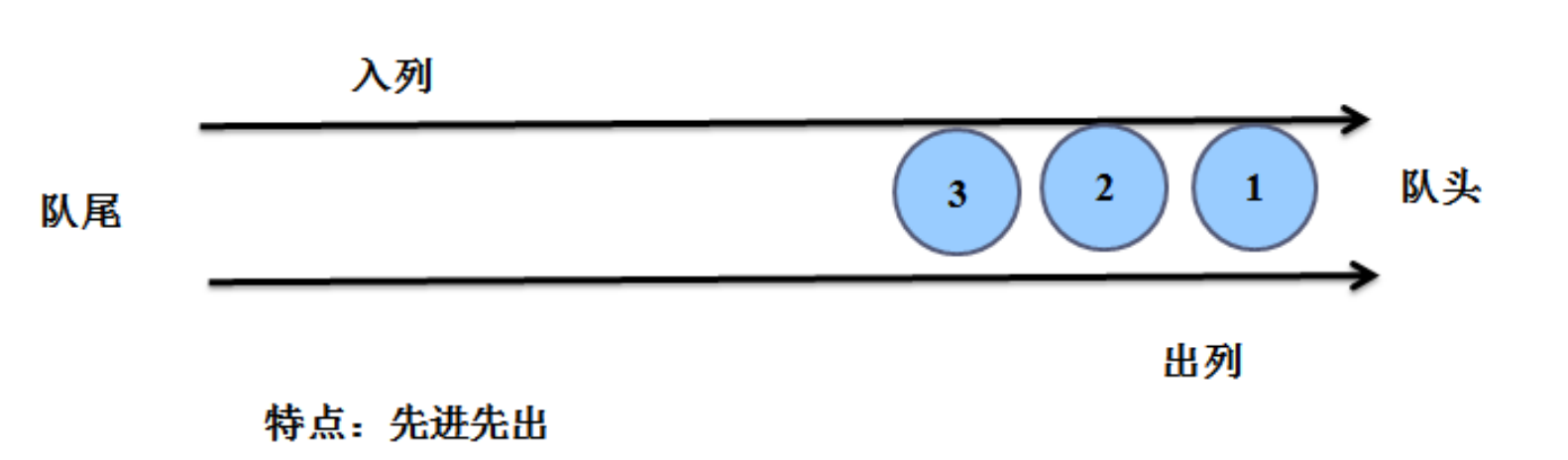
队列(queue)
顺序队列(循环队列) 和 链式队列
1.1 什么是队列?
只允许在两端进行插入和删除操作的线性表,在队尾插入,在队头删除 插入的一端,被称为"队尾",删除的一端被称为"队头"
在队列操作过程中,为了提高效率,以调整指针代替队列元素的移动,并将数组作为循环队列的操作空间。
1.2 队列的特点
先进先出FIFO first in out
后进后出LILO last
1.3 举例:
去银行办理业务,需要排队,有个先来后到,先来的先办业务
2、顺序队列(sequence queue)
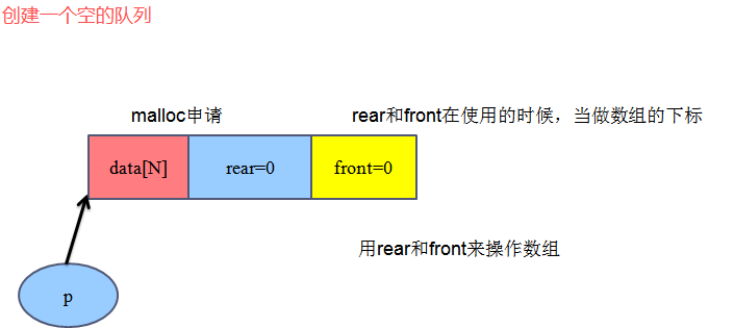
1、创建一个空的队列
#define N 5
typedef int datatype;
typedef struct
{
datatype data[N]; //N= 5(0~4)
int rear; //存数据端 rear 后面
int front; //取数据端 front 前面
}sequeue_t;//sequence 顺序 queue队列
=-1 ->top = -1
top++
判空: rear= 0, front =0;
2、入列
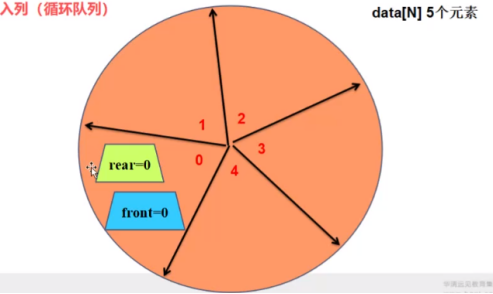
p-p->data[p->rear] = 1;
p->rear++; ->4 =>0
(4+1)%5 = 0;
p->rear = (p->rear+1)%N;
3、出列
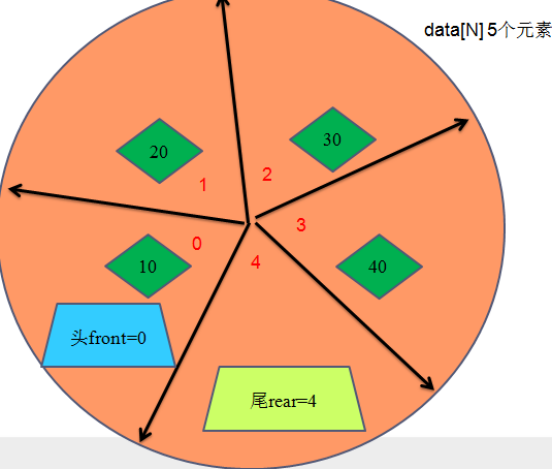
p->data[p->front] = data;
p->front = (p->front +1)%N
p->front = (0+1)%5 = 1;
Rear = (Rear+1) %N;
4、判断队列是否为空
5、判断队列是否为满
6、求队列的长度
7、清空队列
顺序队列操作思想总结: 顺序队列(又称为循环队列)
逻辑结构: 线性结构
存储结构:顺序存储结构
#define N 5
typedef int datatype;
typedef struct
{
datatype data[N];
int rear; //存数据端 rear 后面
int front; //取数据端 front 前面
}sequeue_t;//sequence 顺序 queue队列
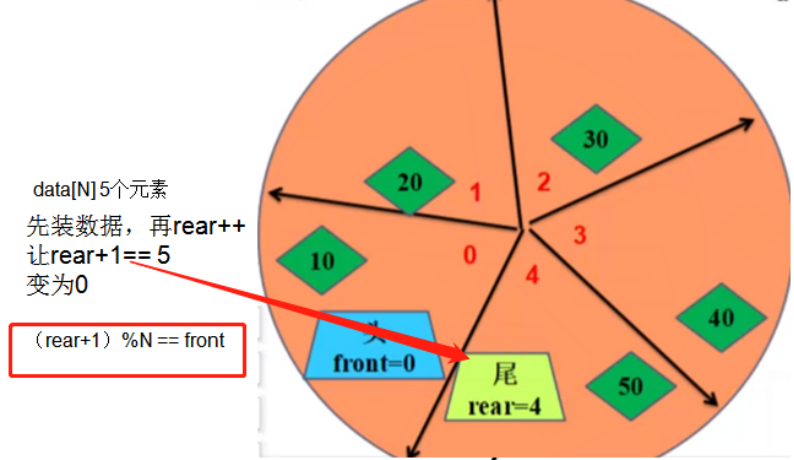
循环队列中,假设数组的元素个数为N,那么循环队列中存储最多的数据个数为N-1个
原因:思想上,舍去数组上的一个存储位置,用于判断队列是否为满,先判断rear的下一个位置是否等于front
return (p->rear+1) % N == p->front;
问题:循环队列,如果数组的元素个数为N,那么队列中最多能够存储的数据数的多少? N-1个为什么?
rear 后面 队尾,在插入的时候,插入之前需要先判断 rear+1,
也就是他的下一个为位置是否等于front 来判断队列是否为满,会造成浪费一个存储位置
顺序队列操作
sequeue.h代码
#ifndef _SQUEUE_H_
#define _SQUEUE_H_
#include <stdio.h>
#include <stdlib.h>
#define N 5
typedef int datatype;
typedef struct
{
datatype data[N]; //循环队列的数组
int rear; //存数据段
int front; //取数据段
}sequeue_t;
sequeue_t *CreateEpSequeue();
int IsfullSequeue(sequeue_t *p);
int InSequeue(sequeue_t *p,datatype data);
int IsEpSequeue(sequeue_t *p);
int OutSequeue(sequeue_t *p);
int LengthSequeue(sequeue_t *p);
void ClearSequeue(sequeue_t *p);
#endif
sequeue.c代码
#include "sequeue.h"
//1、创建一个空的队列
sequeue_t *CreateEpSequeue()
{
sequeue_t *p=(sequeue_t *)malloc(sizeof(sequeue_t));
if (p==NULL)
{
printf("create error");
}
p->front=0;
p->rear=0;
return p;
}
//2、判断队列是否为满
int IsfullSequeue(sequeue_t *p)
{
return (p->rear+1)%N==p->front;
}
//3、入列
int InSequeue(sequeue_t *p,datatype data)
{
if(IsfullSequeue(p))
{
printf("insequeue error");
return -1;
}
//队尾入队
p->data[p->rear]=data;
//标记队尾的下标往后走一步
p->rear=(p->rear+1)%N;
return 0;
}
//4、判断队列是否为空
int IsEpSequeue(sequeue_t *p)
{
return p->front==p->rear;
}
//5、出列
int OutSequeue(sequeue_t *p)
{
if(IsEpSequeue(p))
{
printf("outsequeue error");
return -1;
}
//队头出队
datatype temp=p->data[p->front];
//出队后,标记队头的下标往后走一步
p->front=(p->front+1)%N;
return temp;
}
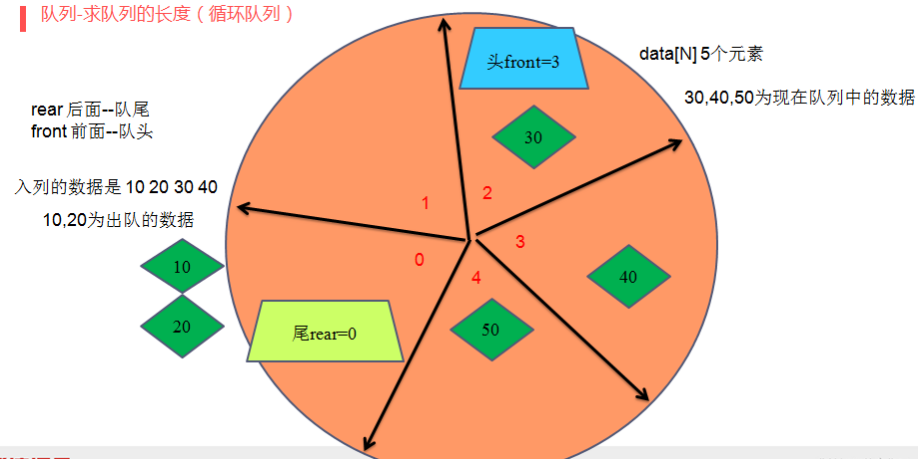
//6、求队列的长度
int LengthSequeue(sequeue_t *p)
{
if(p->rear>=p->front)
{
return p->rear-p->front;
}else
{
return p->rear-p->front+N;
}
}
//7、清空队列函数
void ClearSequeue(sequeue_t *p)
{
p->front=0;
p->rear=0;
}
main.c代码
#include "sequeue.h"
int main(int argc, const char *argv[])
{
sequeue_t *p=CreateEpSequeue();
int i;
for (i=0;i<N-1;i++)
{
InSequeue(p,i);
}
printf("length:%d
",LengthSequeue(p));
for (i=0;i<N-1;i++)
{
printf("%d
",Outequeue(p));
}
return 0;
}
3、 链式队列
链式队列前言
使用有头单向lia
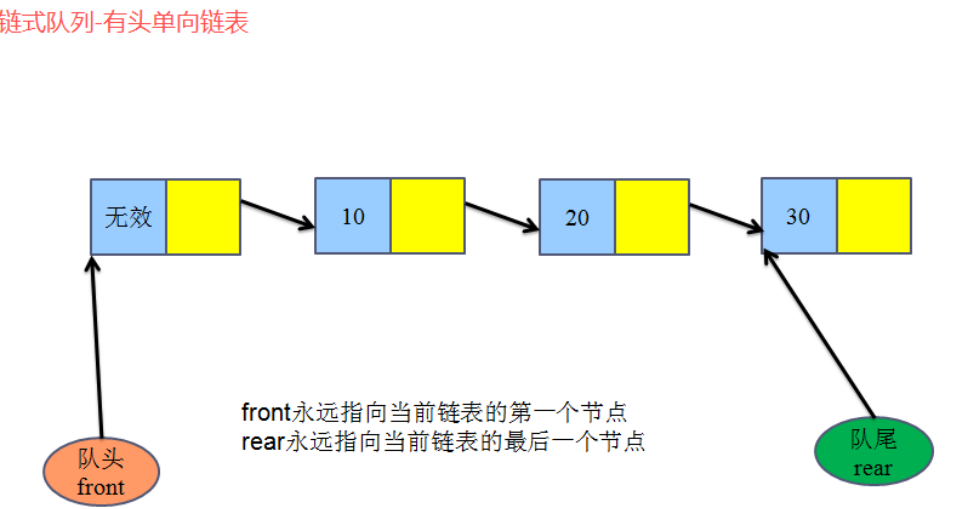
3.1 逻辑结构: 线性结构
3.2 存储结构:链式存储
3.3 链式队列的操作:
typedef struct node
{
datatype data;//数据域
struct node *next;//指针域
}linkqueue_node_t,*linkqueue_list_t;
typedef struct //将队列头指针和尾指针封装到一个结构体里
{
linkqueue_list_t front; //相当于队列的头指针 =>struct node *front linkqueue_list_t rear; //相当于队列的尾指针 =>struct node *rear
//有了链表的头指针和尾指针,那么我们就可以操作这个链表
}linkqueue_t;
linkqueue_t *q; q->front->data
struct node <=>linkqueue_node_t
struct node *<=>linkqueue_node_t *
int *p; p 类型:int *
char *q;q类型:char *
typedef struct node * =>linkqueue_list_t
linkqueue_list_t p <=> struct node *p <=>linkqueue_node_t *p
链式队列操作思想
1、创建一个空的队列
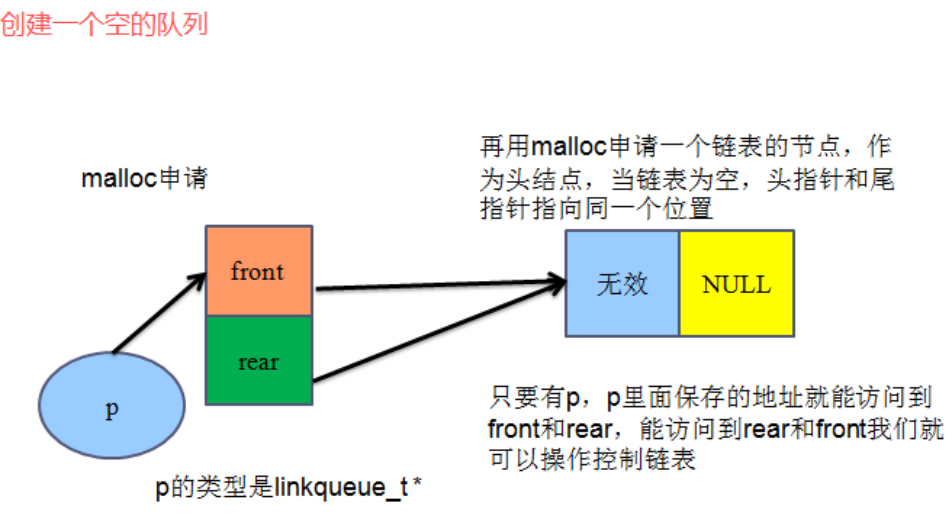
2、入列
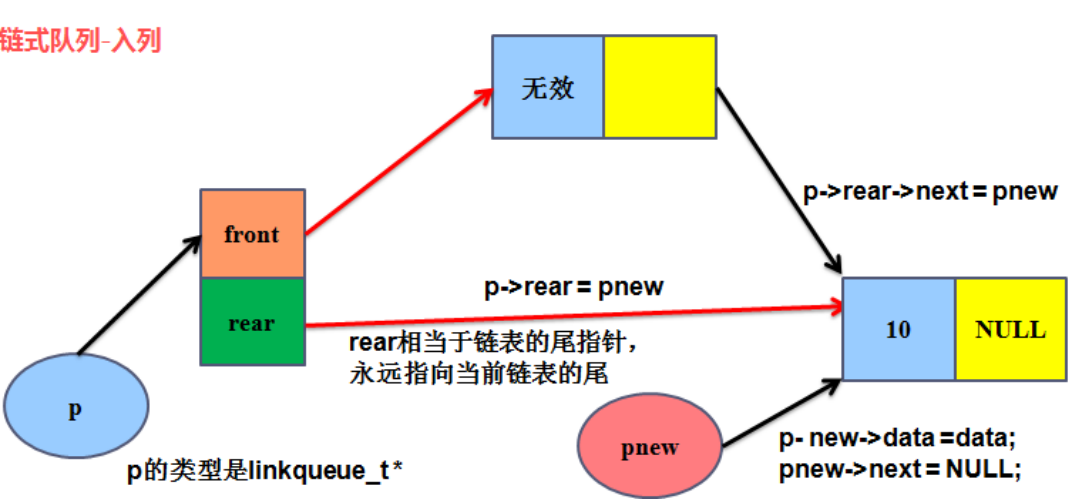
3、出列
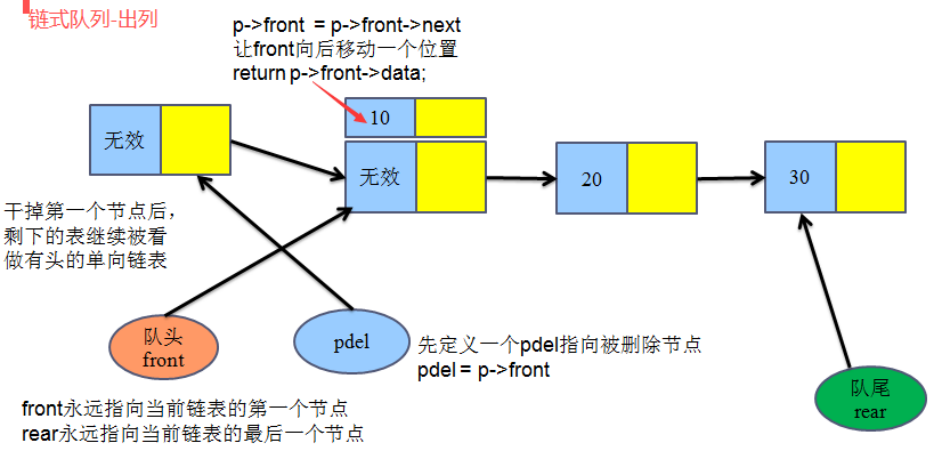
4、判断队列是否为空
5、清空队列
【4】链式队列操作函数
linksequeue.h代码
#ifndef _LINKQUEUE_H_
#define _LINKQUEUE_H_
#include <stdio.h>
#include <stdlib.h>
typedef int datatype;
typedef struct node
{
datatype data; //数据域
struct node *next; //指针域
}linkqueue_node_t,*linkqueue_list_t;
typedef struct //将队头指针和尾指针封装到一个结构体里
{
linkqueue_list_t front; //相当于队列的头指针
linkqueue_list_t rear; //相当于队列的尾指针
}linkqueue_t; //有了链表的头指针和尾指针,那么就可以操作这个链表
linkqueue_t *CreateEpLinkQueue();
int InLinkQueue(linkqueue_t *p,datatype data);
datatype OutLinkQueue(linkqueue_t *p);
datatype IsEpLinkQueue(linkqueue_t *p);
int LengthLinkQueue(linkqueue_t *p);
void ClearLinkQueue(linkqueue_t *p);
#endif
linksequeue.c代码
#include "linkqueue.h"
//1、创建一个空的队列
linkqueue_t *CreateEpLinkQueue()
{
linkqueue_t *p=(linkqueue_t *)malloc(sizeof(linkqueue_t));
if (p==NULL)
{
printf("CreateEpLinkQueue malloc error");
return NULL;
}
p->front=(linkqueue_list_t)malloc(sizeof(linkqueue_node_t));
if (p->front==NULL)
{
printf("malloc error");
return NULL;
}
p->front->next=NULL;
p->rear=p->front;
return p;
}
//2、入列
datatype InLinkQueue(linkqueue_t *p,datatype data)
{
linkqueue_list_t pnew=(linkqueue_list_t)malloc(sizeof(linkqueue_node_t));
if (pnew==NULL)
{
printf("pnew malloc error");
return -1;
}
//初始化节点
pnew->data=data;
pnew->next=NULL;
//队尾入队
p->rear->next=pnew;
//队尾指针指向新的尾节点
p->rear=pnew;
return 0;
}
//3、出列
datatype OutLinkQueue(linkqueue_t *p)
{
if(IsEpLinkQueue(p))
{
printf("OutLinkQueue error");
return -1;
}
//队头出队,有头单向链表,头结点是无效节点 ,最后留最后一个元素为头结点
linkqueue_list_t pdel=NULL;
pdel=p->front; //pdel指向头结点
p->front=pdel->next; //front指向头结点的下一个节点
free(pdel);
pdel=NULL;
return p->front->data; //取出数据域
#if 0
datatype temp; //最后留下的是头结点
linkqueue_list_t pdel=NULL;
pdel=p->front->next;
p->front->next=pdel->next;
temp=pdel->data;
free(pdel);
pdel=NULL;
return temp;
#endif
}
//4、判断队列是否为空
datatype IsEpLinkQueue(linkqueue_t *p)
{
return p->front->next==NULL;
}
//5、求队列长度的函数
int LengthLinkQueue(linkqueue_t *p)
{
int len=0;
if(IsEpLinkQueue)
{
printf("LengthLinkQueue error");
return -1;
}
linkqueue_list_t h=p->front;
while (h->next!=NULL)
{
h=h->next;
len++;
}
return len;
}
//6、清空队列
void ClearLinkQueue(linkqueue_t *p)
{
while(!IsEpLinkQueue)
{
OutLinkQueue(p);
}
}
main.c代码
#include "linkqueue.h"
int main(int argc, const char *argv[])
{
linkqueue_t *p=CreateEpLinkQueue();
int i;
for(i=0;i<5;i++)
{
InLinkQueue(p,i);
}
for(i=0;i<5;i++)
{
printf("%d
",OutLinkQueue(p));
}
free(p->rear);
p->rear=NULL;
free(p);
p=NULL;
#if 0
free(p->front);
p->front=NULL;
free(p);
p=NULL;
#endif
return 0;
}
三、树
1. 树的前言
概念:
树(Tree)是(n>=0)个节点的有限集合T,它满足两个条件 :有且仅有一个特定的称为根(Root)的节点;其余的节点可以分为m(m≥0)个互不相交的有限集合T1、T2、……、Tm,其中每一个集合又是一棵树,并称为其根的子树(Subtree)。
特征:
一对多,每个节点最多有一个前驱,但可以有多个后继(根节点无前驱,叶节点无后继)
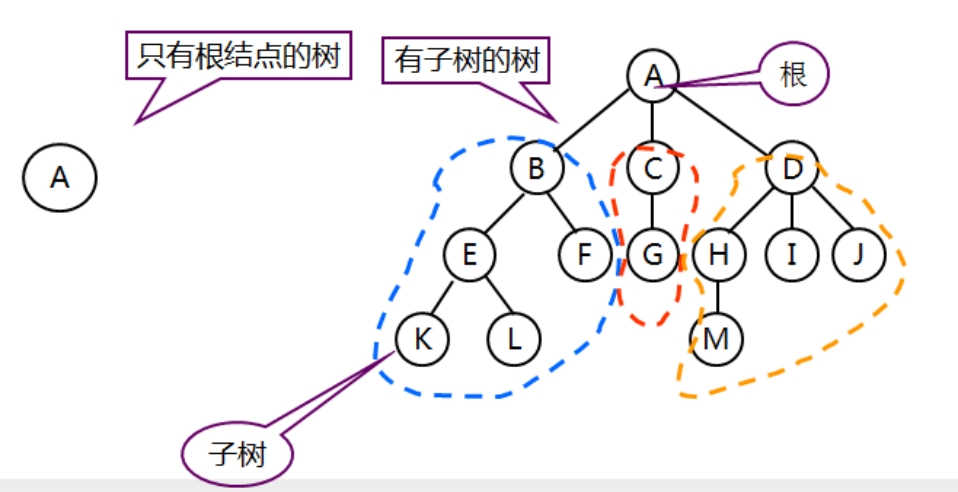
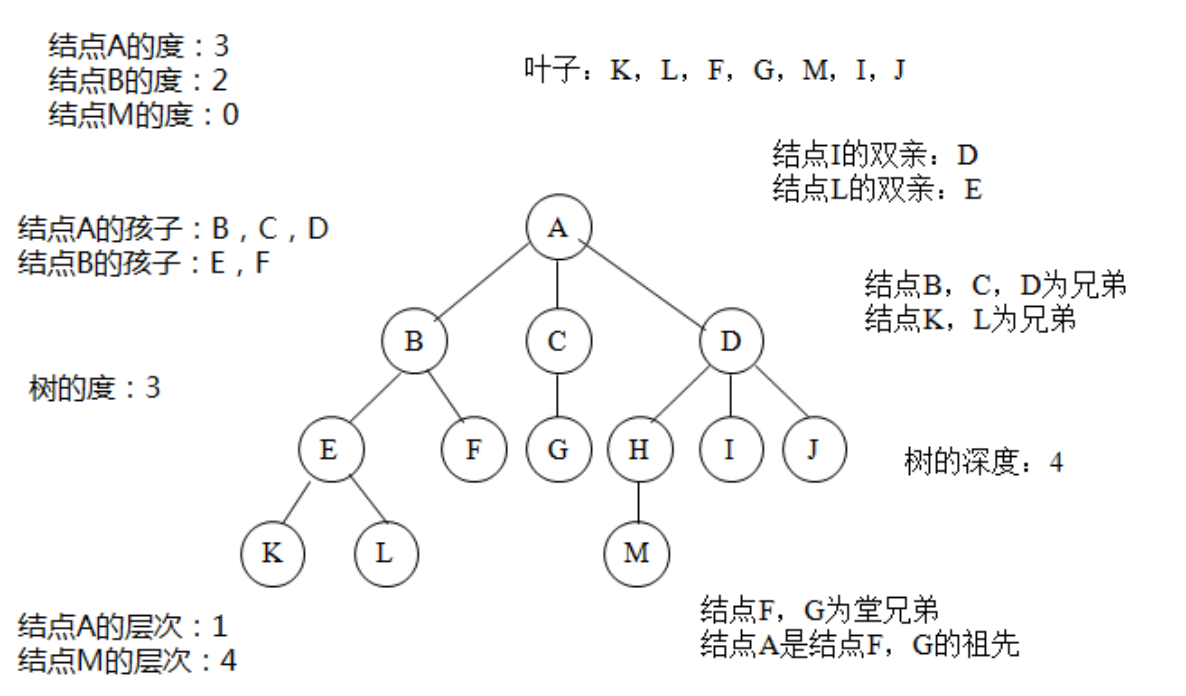
1.1 关于树的一些基本念
(1)度数:一个节点的子树的个数(一个节点的子树的个数称为该节点的度数,3)
(2)树度数:树中节点的最大度数
(3)叶节点或终端节点: 度数为零的节点
(4)分支节点:度数不为零的节点(B一层)
(5)内部节点:除根节点以外的分支节点 (B,C,D)
(6)节点层次: 根节点的层次为1,根节点子树的根为第2层,以此类推
(7)树的深度或高度: 树中所有节点层次的最大值 (4)
1.2 二叉树
1.2.1 概念
二叉树(Binary Tree)是n(n≥0)个节点的有限集合,它或者是空集(n=0),
或者是由一个根节点以及两棵互不相交的、分别称为左子树和右子树的二叉树组成。
二叉树与普通有序树不同,二叉树严格区分左孩子和右孩子,即使只有一个子节点也要区分左右。
二叉树:节点最大的度数2
1.2.2 二叉树性质(重点)
(1)二叉树第k(k>=1)层上的节点最多为2的k-1次幂个。
(2)深度为k(k>=1)的二叉树最多有2的k次幂-1个节点。//满二叉树的时候
(3)在任意一棵二叉树中,树叶的数目比度数为2的节点的数目多一
笔试题:
一棵二叉树有8个度为2的节点,5个度为1的节点,那么度为0的节点个数为( D ) (网易)
A 不确定 B 7 C 8 D 9 E 6
任意一颗二叉树,度数0 比 度数2节点 多 1 n0 = n2 + 1
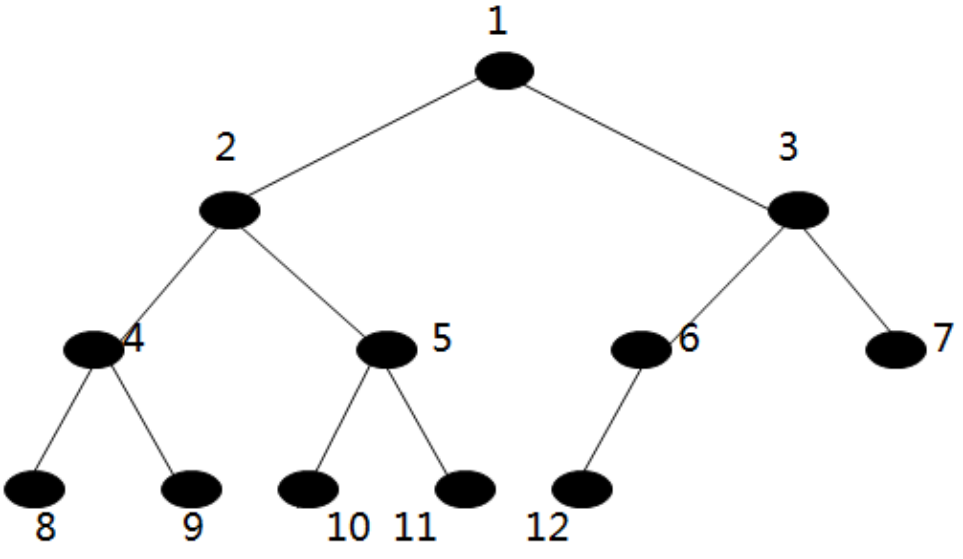
(4)满二叉树和完全二叉树
1、满二叉树: 深度为k(k>=1)时节点为2^k - 1(2的k次幂-1)
2、完全二叉树:只有最下面两层有度数小于2的节点,且最下面一层的叶节点集中在最左边的若干位置上。完全二叉树最多只有一个度为1的分支节点。

2、顺序存储结构
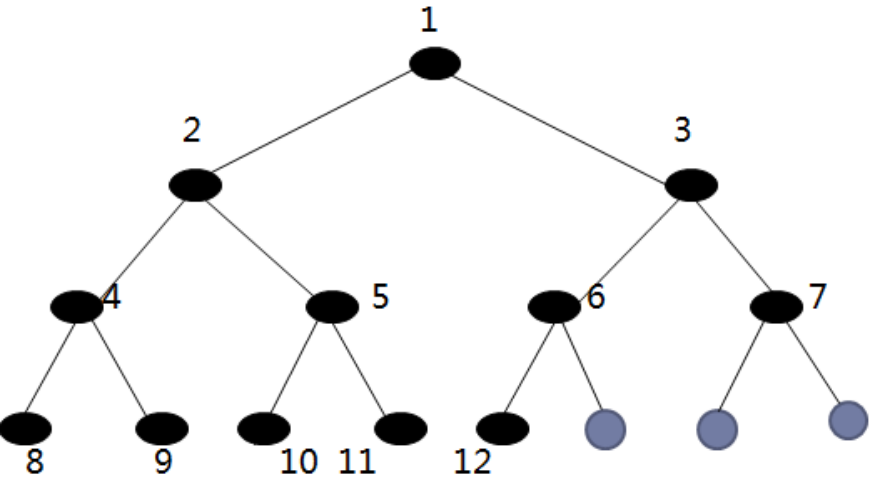
顺序存储结构 :
完全二叉树节点的编号方法是从上到下,从左到右,根节点为1号节点。
设完全二叉树的节点数为n ,某节点编号为i
当i>1(不是根节点)时,有父节点,其编号为i/2;
当2*i<=n时,有左孩子,其编号为2*i ,否则没有左孩子,本身是叶节点;
当2*i+1<=n时,有右孩子,其编号为2*i+1 ,否则没有右孩子;
- 节点编号
根节点编号1
根节点左子节点编号:2 即 2 * 1
根节点右子节点编号:3 即 2 * 1 + 1
第n个节点
左子节点编号:2 * n
右子节点编号:2 * n + 1
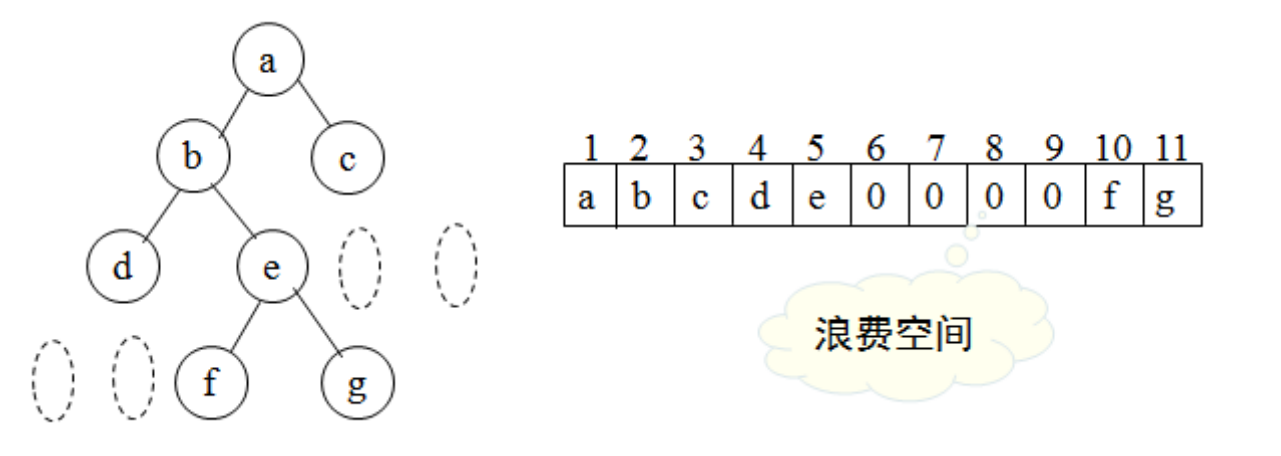
有n个节点的完全二叉树可以用有n+1 个元素的数组进行顺序存储,节点号和数组下标一一对应,下标为零的元素不用。
利用以上特性,可以从下标获得节点的逻辑关系。不完全二叉树通过添加虚节点构成完全二叉树,然后用数组存储,这要浪费一些存储空间.
【2】树的遍历
树的遍历
- 二叉树的遍历(重点)
前序: 根----> 左 -----> 右 abdefgc
中序: 左----> 根 -----> 右 dbfegac
后序: 左----> 右 -----> 根 dfgebca
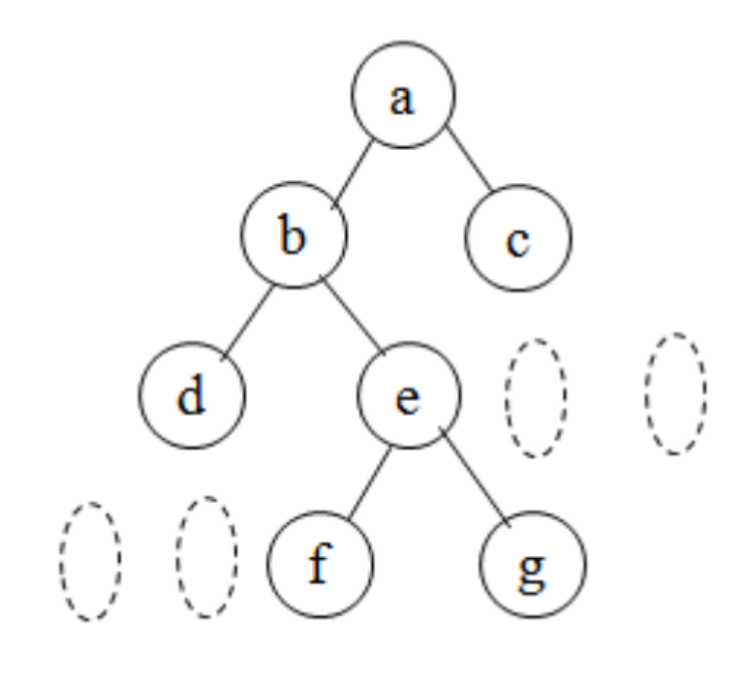
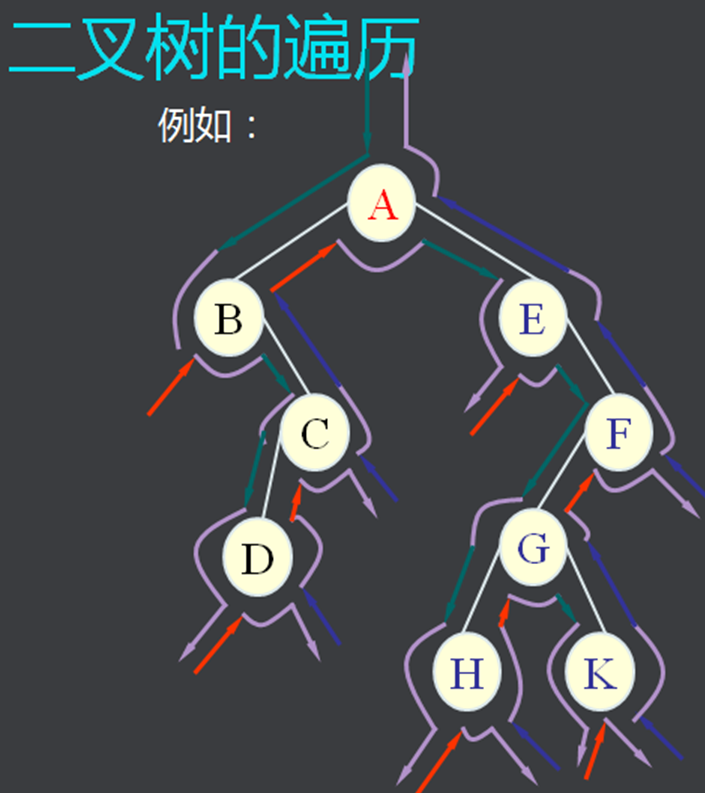
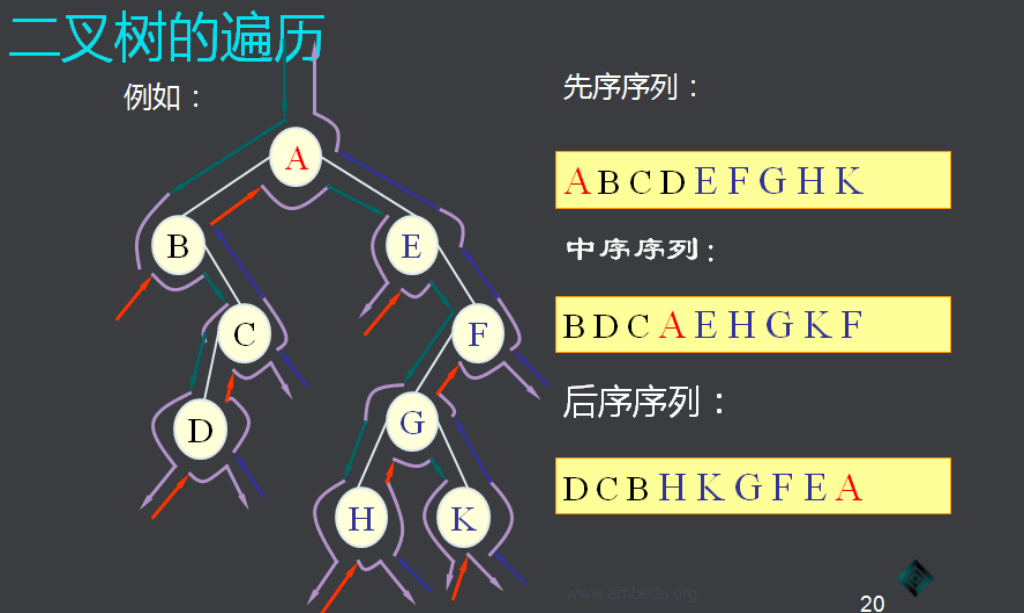
练习:
已知遍历结果如下,试画出对应的二叉树(后序)
前序:A B C E H F I J D G K
中序:A H E C I F J B D K G
唯一一颗二叉树:
前序和中序
中序和后序
3、二叉树的链式存储 (节点(结构体))
解题思想和操作函数
1
2 3
当i>1(不是根节点)时,有父节点,其编号为i/2;
当2*i<=n时,有左孩子,其编号为2*i ,否则没有左孩子,本身是叶节点;
当2*i+1<=n时,有右孩子,其编号为2*i+1 ,否则没有右孩子;
#ifndef _BITREE_H_
#define _BITREE_H_
typedef int datatype_tree;
typedef struct tree_node_t
{
datatype_tree data;//数据域
struct tree_node_t *lchild;//左子left
struct tree_node_t *rchild;//右子right
}bitree_node_t,*bitree_list_t;
bitree_list_t CreateBitree(int n,int i);
//前序
void PreOrder(bitree_list_t r);
//中序
void InOrder(bitree_list_t r);
//后序
void PostOrder(bitree_list_t r);
//层次
void unOrder(bitree_list_t *r);
bitree.h代码
#ifndef _BITREE_H_
#define _BITREE_H_
#include <stdio.h>
#include <stdlib.h>
typedef int datatype;
typedef struct tree_node_t
{
datatype data;
struct tree_node_t *lchild;
struct tree_node_t *rchild;
}bitree_node_t,*bitree_list_t;
bitree_list_t CreateBitree(int n,int i);
void PreOrder(bitree_list_t r);
void InOrder(bitree_list_t r);
void PostOrder(bitree_list_t r);
void unOrder(bitree_list_t r);
#endif
bitree.c代码
#include "bitree.h"
bitree_list_t CreateBitree(int n,int i)
{
bitree_list_t r=(bitree_list_t)malloc(sizeof(bitree_node_t));
if (r==NULL)
{
printf("malloc bitree_node_t error");
return NULL;
}
r->data=i;
if(2*i<=n)
{
r->lchild=CreateBitree(n,2*i);
}else
{
r->lchild=NULL;
}
if(2*i+1<=n)
{
r->rchild=CreateBitree(n,2*i+1);
}else
{
r->rchild=NULL;
}
return r;
}
void PreOrder(bitree_list_t r)
{
if (r==NULL)
{
return;
}
printf("%d",r->data);
if(r->lchild!=NULL)
{
PreOrder(r->lchild);
}
if(r->rchild!=NULL)
{
PreOrder(r->rchild);
}
}
void InOrder(bitree_list_t r)
{
if (r==NULL)
{
return;
}
if(r->lchild!=NULL)
{
InOrder(r->lchild);
}
printf("%d",r->data);
if(r->rchild!=NULL)
{
InOrder(r->rchild);
}
}
void PostOrder(bitree_list_t r)
{
if (r==NULL)
{
return;
}
if(r->lchild!=NULL)
{
PostOrder(r->lchild);
}
if(r->rchild!=NULL)
{
PostOrder(r->rchild);
}
printf("%d",r->data);
}
main.c代码
#include "bitree.h"
int main(int argc, const char *argv[])
{
bitree_list_t r=CreateBitree(3,1);
PreOrder(r);
putchar(10);
InOrder(r);
putchar(10);
PostOrder(r);
putchar(10);
return 0;
}
//层次遍历
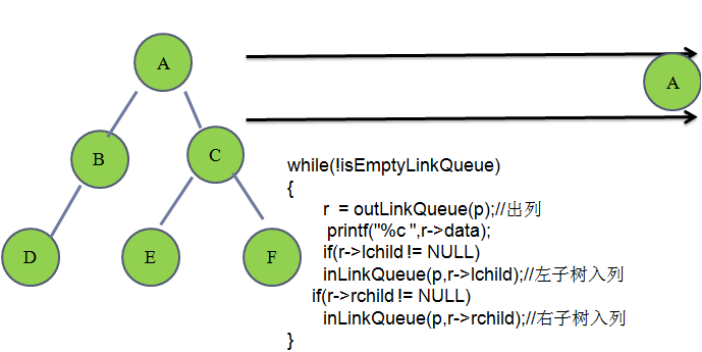
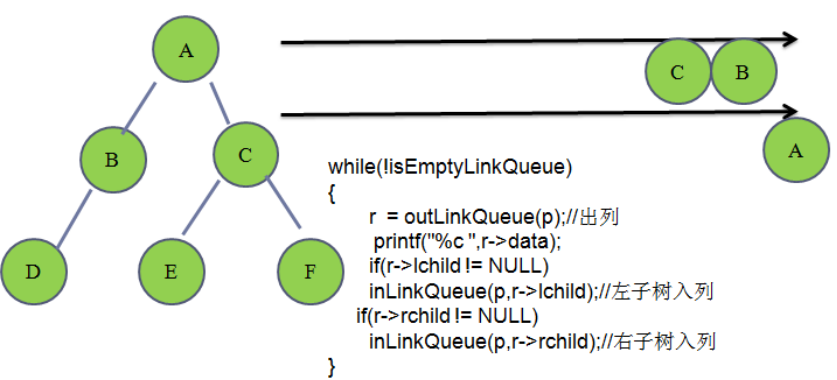
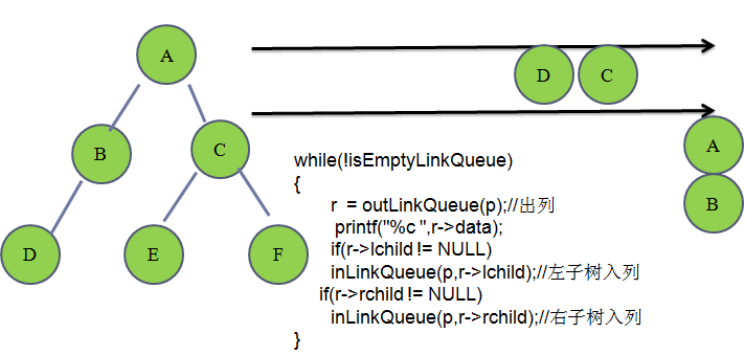
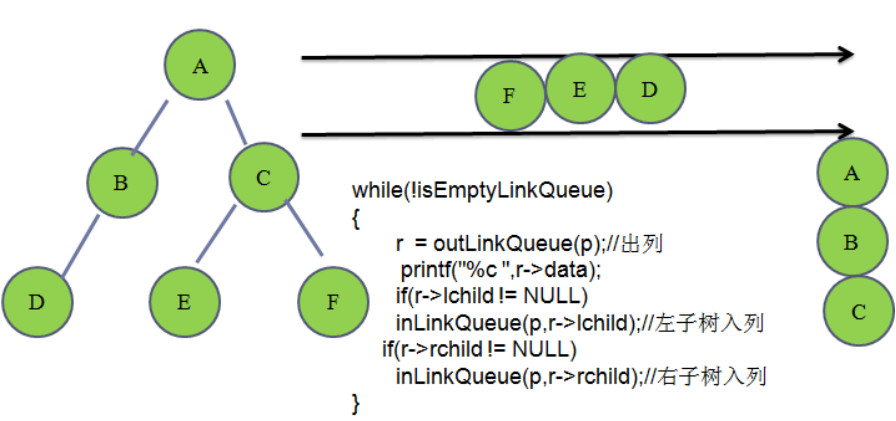
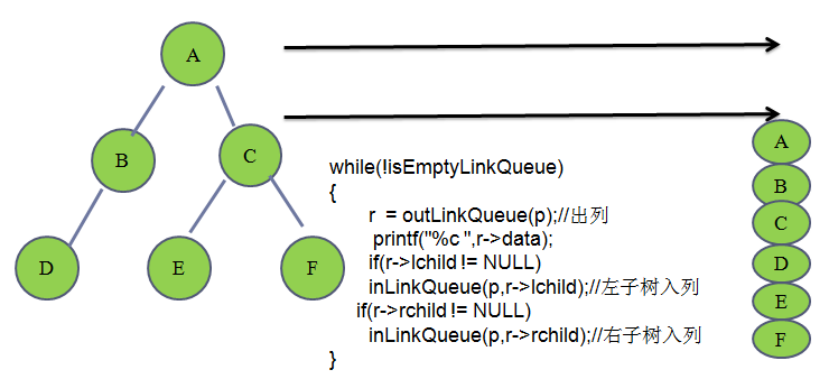
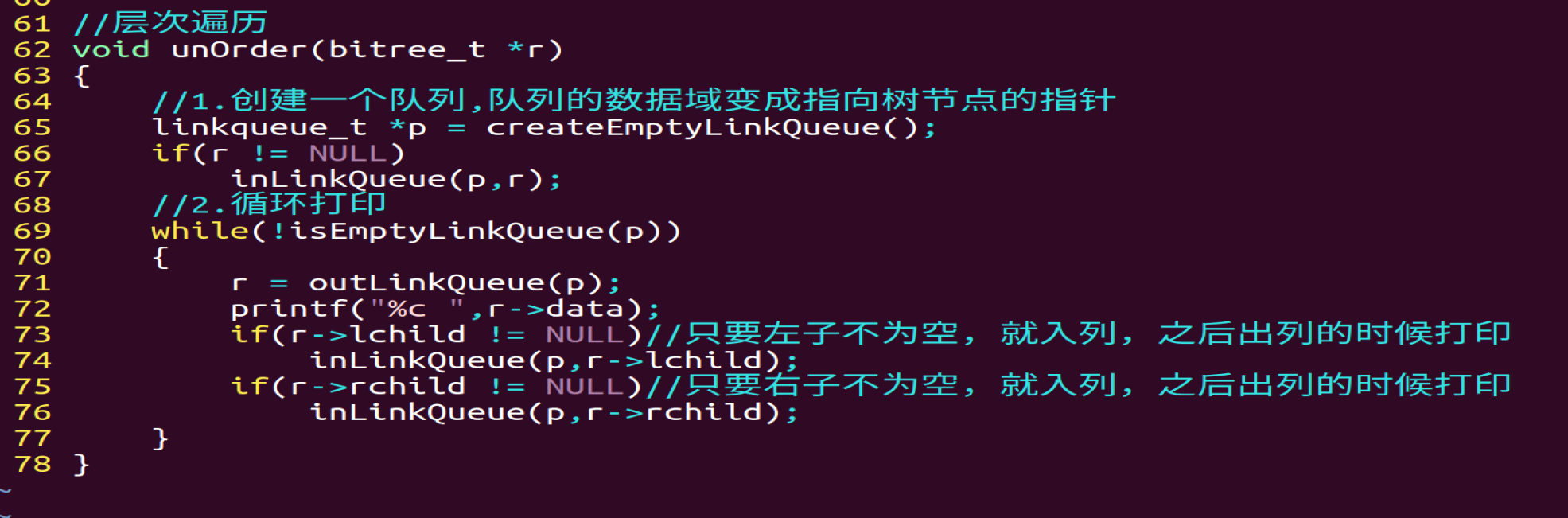
笔试题:
1、深度为8的二叉树,其最多有( ) 个节点,第8层最多有( )个节点
(网易)
2、数据结构中,沿着某条路线,一次对树中每个节点做一次且仅做一次访问,对二叉树的节点从1开始进行连续编号,要求每个节点的编号大于其左、右孩子的编号,同一节点的左右孩子中,其左孩子的编号小于其右孩子的编号,可采用( )次序的遍历实现编号(网易)
//左 右 根
A 先序 B 中序 C 后序 D 从根开始层次遍历
3、一颗二叉树的 前序: A B D E C F, 中序:B D A E F C 问树的深度是 ( B ) (网易)
A 3 B 4 C 5 D 6
四、知识点扩展
双向链表前言
1.1 逻辑结构:线性结构
1.2 存储结构:链式存储
1.3 操作:增 删 改 查
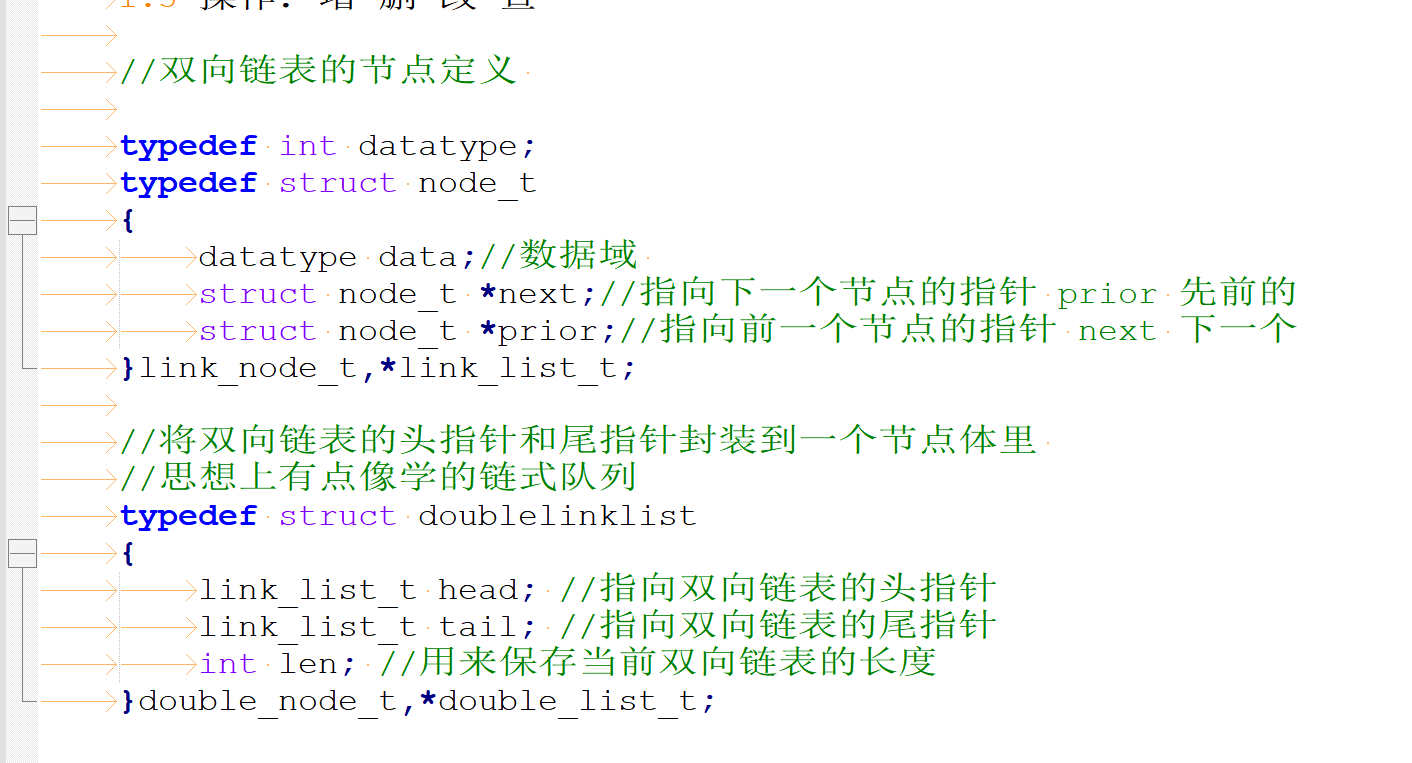
//双向链表的节点定义
typedef int datatype;
typedef struct node_t
{
datatype data;//数据域
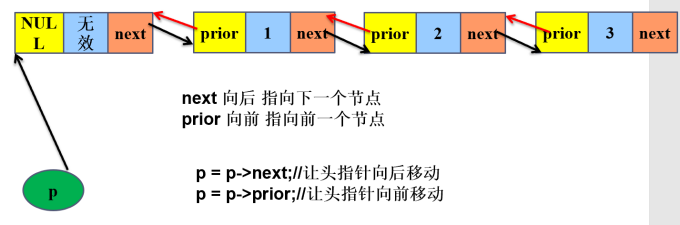
struct node_t *next;//指向下一个节点的指针 prior 先前的
struct node_t *prior;//指向前一个节点的指针 next 下一个
}link_node_t,*link_list_t;
//将双向链表的头指针和尾指针封装到一个节点体里
//思想上有点像学的链式队列
typedef struct doublelinklist
{
link_list_t head; //指向双向链表的头指针
link_list_t tail; //指向双向链表的尾指针
int len; //用来保存当前双向链表的长度
}double_node_t,*double_list_t;
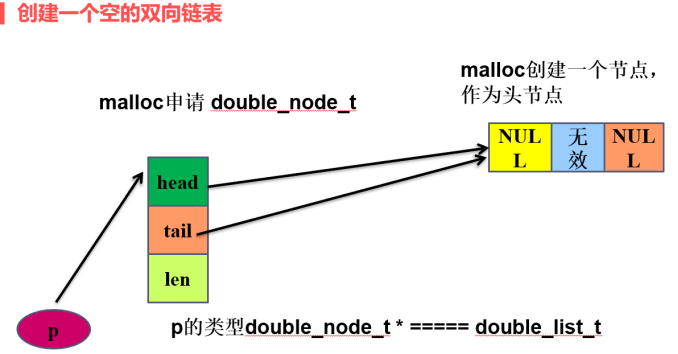
1、双向链表实现思想和代码
1)创建一个空的双向链表
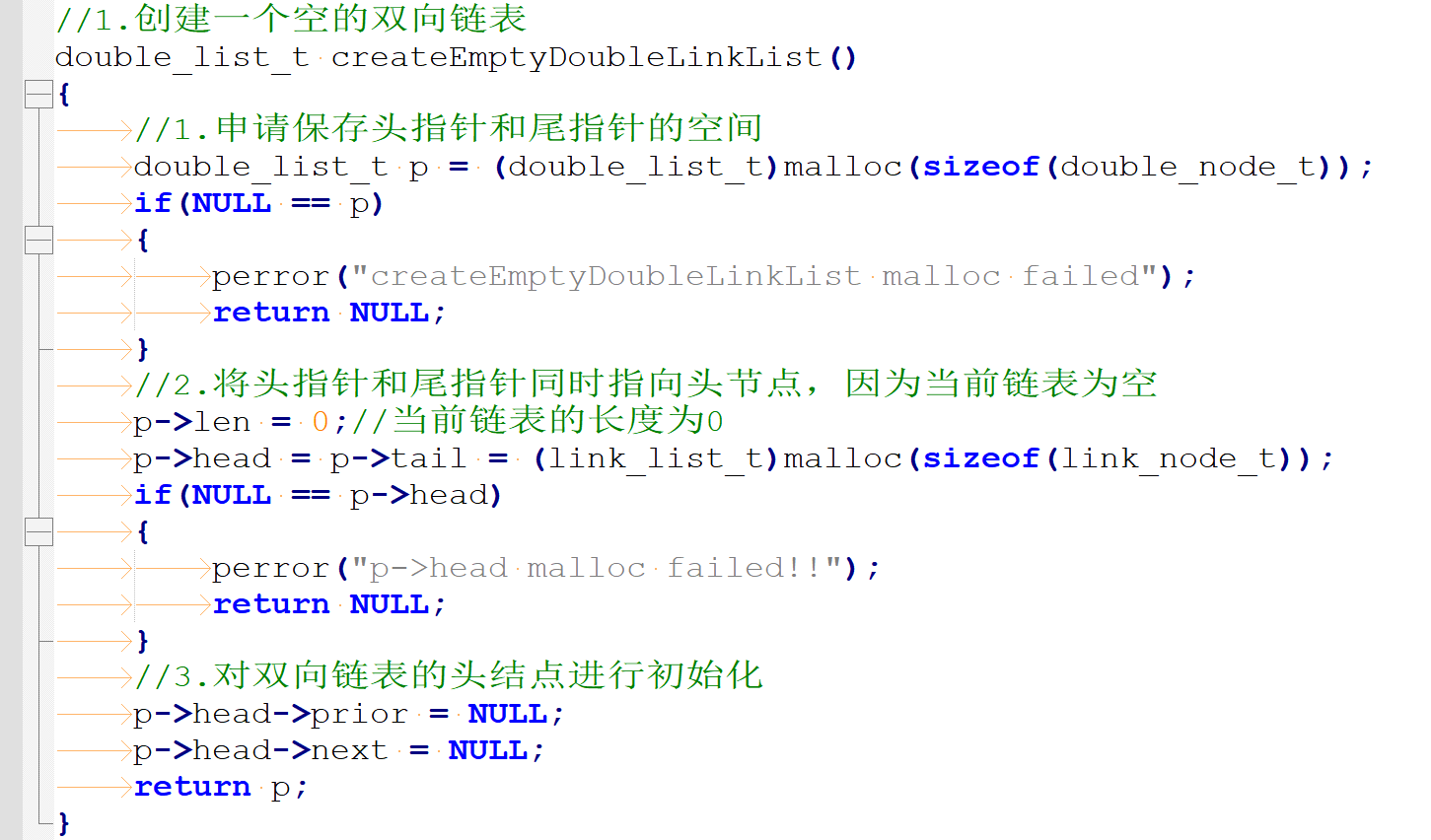
2)双向链表中间插入
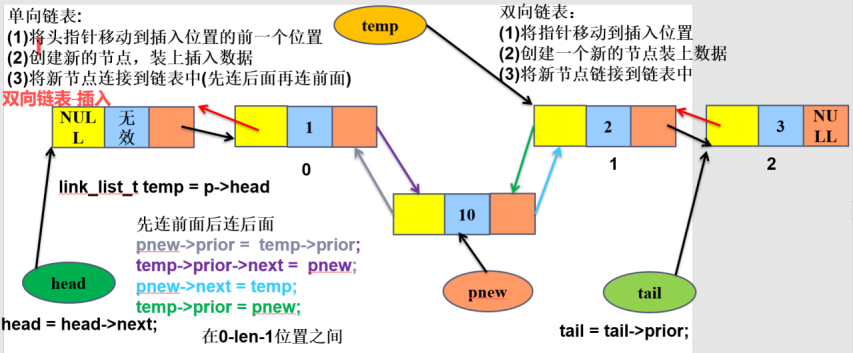

3)双向链表尾插
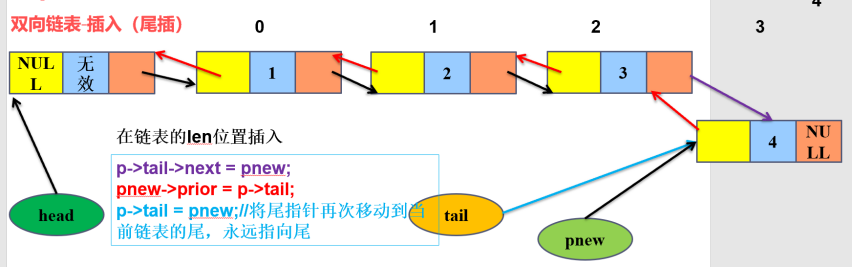
4)双线链表中间删除
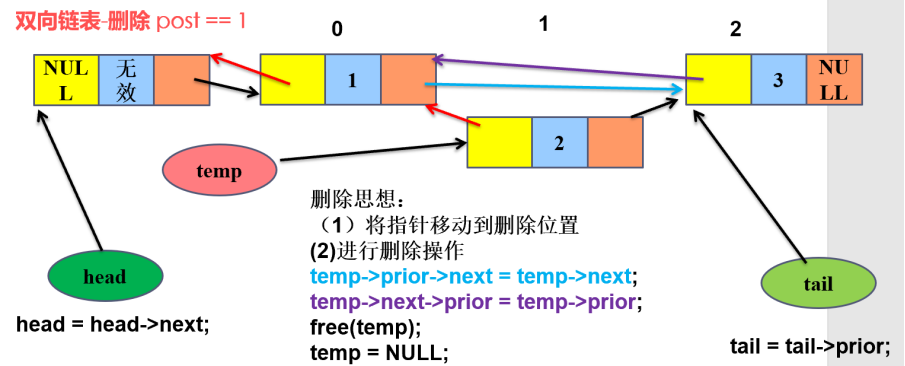
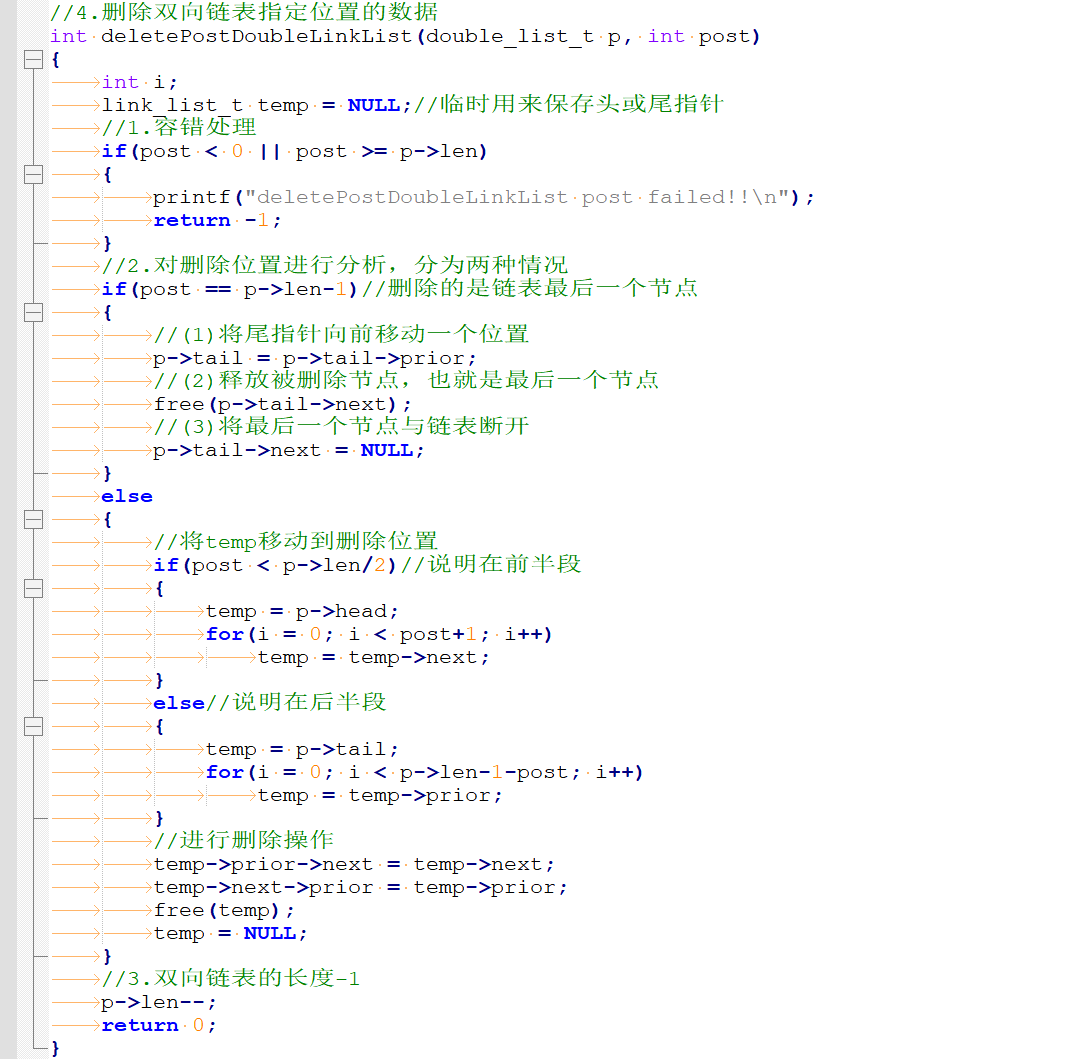
5)双线链表删除最后一个节点
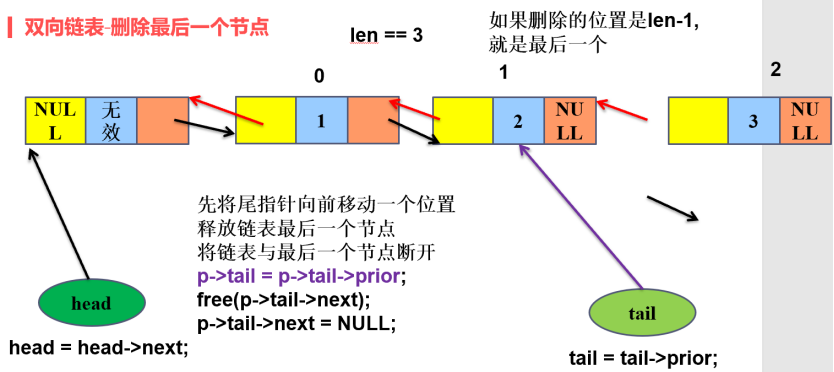
2、算法
(1)查找
1.1、顺序查找
代码练习
(1)main函数中定义一个数组int a[10] = {12,34,45,23,54,2,4,65,23}
(2)定义一个函数,查找指定数据
(3)如果找到了,返回它的位置,数组下标即可,未找到返回-1
(4)main函数中测试
//p 保存数组首地址,n元素个数,value 要查找的值
findByOrder(int *p, int n,int value)
#include <stdio.h>
int findByOrder(int *p,int n,int value)
{
int i;
for(i = 0; i < n; i++)
{
if(p[i] == value)
{
return i; //返回数组下标
}
}
return -1; //如果程序能执行到这肯定没找到
}
int main()
{
int a[10] = {12,34,54,23,12,3453,564,23,121,9};
int num;
int ret;
puts("Please input num:");
scanf("%d",&num);
ret = findByOrder(a,10,num);
if(ret == -1)
{
printf("Not find %d ",num);
}
else
{
printf("find %d ",a[ret]);
}
return 0;
}
顺序查找:当数据较多时int a[1000],查找慢;
1.2、二分查找
代码练习
二分法查找(又叫分半查找、拆半查找)
### 前提条件:数组中元素必须为有序序列
思想: 每次进行分半,判断在middle的左边还是右边
#include <stdio.h>
//二分查找 value代表的是被查找的值
int findByHalf(int *p, int n, int value)
{
int low = 0;//low低
int high = n-1;//high高
int middle;//用来保存中间位置的下标
while(low <= high)//注意此处循环结束的条件,需要加上 =
{
//不断获取中间位置的下标
middle = (low + high) / 2;
if(value < p[middle])//说明在前半段,移动high
{
high = middle-1;
}
else if(value > p[middle])//说明在后半段,移动low
{
low = middle + 1;
}
else//对应p[middle] == value 情况
{
return middle;
}
}
return -1;//代表没有找到
}
int main(int argc, const char *argv[])
{
int a[] = {12,34,56,77,89,342,567,7898};
int i;
for(i = 0; i < sizeof(a)/sizeof(a[0]); i++)//把数组中的每个元素都找一遍,进行测试程序
{
printf("%d post is %d ",a[i],findByHalf(a,sizeof(a)/sizeof(a[0]),a[i]));
}
//查找10000返回 -1
printf("%d post is %d ",10000,findByHalf(a,sizeof(a)/sizeof(a[0]),10000));
return 0;
}
1.3、分块查找
代码练习
索引存储
索引表 + 源数据表
条件:
块间有序,块内无序
思路:
(1)先在索引表中确定在哪一块中
(2)再遍历这一块进行查找
//索引表
typedef struct
{
int max; //块中最大值
int post;//块的起始位置下标,post数组下标
}index_t; //索引
//源数据表
int a[19] = {18, 10, 9, 8, 16, 20, 38, 42, 19, 50, 84, 72, 56, 55, 76, 100, 90, 88, 108};
0 5 10 15
//索引表
index_t b[4] = {{18,0},{50,5},{84,10},{108,15}};
****************************************************************************************
#include <stdio.h>
//索引表
typedef struct
{
int max; //块中最大值
int post;//块的起始位置下标,post数组下标
}index_t; //索引
//a原数据表 index_list 索引表 value 被查找的值
int findByBlock(int *a, index_t *index_list,int value)
{
//start和end作为源数据表的下标取搜索
int start;//保存起始下标
int end;//终止下标的后一个位置
//1.思想,先确定value在哪一块中,遍历索引表与每块中的最大值进行比较
int i;
for(i = 0; i < 4; i++)
{
if(value <= index_list[i].max)//说明value有可能在i块中
{
//确定当前i块中的起始下标和终止
start = index_list[i].post;
//假设value在最后一块中,i+1数组越界,所以end的赋值,需要进行条件判断
if(i == 3)//说明在最后一个块
{
end = 19;
}
else
{
end = index_list[i+1].post;
}
break;//注意此处一定要有break
}
}
//确定块的起点和终点后,对源数据表进行遍历
for(i = start; i < end; i++)
{
if(a[i] == value)
return i;
}
return -1;
}
int main(int argc, const char *argv[])
{
int i;
//源数据表
int a[19] = {18, 10, 9, 8, 16, 20, 38, 42, 19, 50, 84, 72, 56, 55, 76, 100, 90, 88, 108};
// 0 4 5 10 15
//索引表,结构体数组
index_t index_list[4] = {{18,0},{50,5},{84,10},{108,15}};
for(i = 0; i < 19; i++)//把源数据表中的每一个数据查询一遍,测试程序
{
printf("%d post is %d ",a[i],findByBlock(a,index_list,a[i]));
}
printf("%d post is %d ",22,findByBlock(a,index_list,22));
return 0;
}
1.4、散列存储
哈希表(hash 哈希函数)
散列存储
有一张表,保存了数据中关键字与对应存储位置的关系
在选择key的时候,要选择数据中不重复的关键字作为key
存时按照对应关系存
取时按照对应关系取
4.1 直接地址法
####练习1####
//保存数据 年龄 + 年龄对应的人口数
10 100
20 300
输入年龄和人口数,按照对应关系保存到哈希表中,
输入要查询的年龄,打印输出该年龄的人口数
#include <stdio.h>
//哈希函数,代表了数据中的关键字与存储位置之间的关系
//调用哈希函数能够得到数据的存储位置
int hashFun(int key)
{
int post = key-1;//key-1代表关系 post通过关系得到存储位置
return post;
}
//存储数据到哈希表,存的时候按照对应的关系存
void saveAgeNum(int *hash_list,int key,int num)
{
//1.通过key得到数据存储的位置,调用哈希函数
int post = hashFun(key);
//2.将数据存储到哈希表中
hash_list[post] = num;
}
//从哈希表中取数据,取的时候按照对应的关系取
int getAgeNum(int *hash_list,int key)
{
//1.通过key得到数据存储的位置,调用哈希函数
int post = hashFun(key);
//2.将数据取出
return hash_list[post];
}
int main(int argc, const char *argv[])
{
int i;
int age,num;//年龄和对应年龄的人口数
int hash_list[200] = { 0 };//哈希表,用来保存年龄和对应年龄的人口数,之所以长度为200,暂定人的寿命为200岁
for(i = 0; i < 4; i++)
{
printf("请您输入年龄和年龄对应的人口数: ");//输入四组数据保存到哈希表中
scanf("%d %d",&age,&num);
//将输入的数据保存到哈希表中
saveAgeNum(hash_list,age,num);
}
//进行查找对应年龄的人口数
for(i = 0; i < 6; i++)
{
printf("请您输入要查询的年龄: ");
scanf("%d",&age);
printf("%d: %d人 ",age,getAgeNum(hash_list,age));
}
return 0;
}
4.2 数字分析法
//k1 k2 k3 k4 k5 k6
//2 3 1 5 8 6
//2 4 2 3 4 6
//2 3 3 7 9 6
//2 3 9 8 8 6
//2 4 5 7 8 6
//2 3 4 2 9 6
//通过数字分析,只有中间两位数重复的次数最少
#include <stdio.h>
//哈希函数
int hashFun(int key)
{
int post = key % 10000 / 100;
return post;
}
//将数据存储
void saveNum(int *hash_list,int key)
{
int post = hashFun(key);
hash_list[post] = key;
}
//将数据取出
int getNum(int *hash_list,int key)
{
int post = hashFun(key);
return hash_list[post];
}
int main(int argc, const char *argv[])
{
//k1 k2 k3 k4 k5 k6
//2 3 1 5 8 6
//2 4 2 3 4 6
//2 3 3 7 9 6
//2 3 9 8 8 6
//2 4 5 7 8 6
//2 3 4 2 9 6
int i;
int a[] = {231586,242346,233796,239886,245786,234296};
//创建哈希表
int hash_list[100];//100因为只取中间两位所以post为两位数
//将数据存入哈希表
for(i = 0; i < sizeof(a)/sizeof(a[0]); i++)
saveNum(hash_list,a[i]);
//查找数据
for(i = 0; i < sizeof(a)/sizeof(a[0]); i++)
printf("post:%d --- %d ",hashFun(a[i]),getNum(hash_list,a[i]));
return 0;
}
/
4.3 平方取中法
当取key中的某些值,不能是记录均匀分布时,根据数学原理,对key进行key的2次幂(取平方)
取key平方中的某些位可能会比较理想
key key的平方 H(key)
0100 00 100 00 100
0110 00 121 00 121
1010 10 201 00 201
1001 10 020 01 020
0111 00 123 21 123
#include <stdio.h>
// key key的平方 H(key)
// 0100 00 100 00 100
// 0110 00 121 00 121
// 1010 10 201 00 201
// 1001 10 020 01 020
// 0111 00 123 21 123
//对key平方后,发现中间的三位重复次数最少
//哈希函数
int hashFun(int key)
{
int post = key*key % 100000 / 100;
return post;
}
//存储数据
void saveNum(int *hash_list, int key)
{
int post = hashFun(key);
hash_list[post] = key;
}
//取数据
int getNum(int *hash_list,int key)
{
int post = hashFun(key);
return hash_list[post];
}
int main(int argc, const char *argv[])
{
int i;
int a[] = {100,110,1010,1001,111}; //key
int hash_list[1000] = { 0 };//哈希表
for(i = 0; i < sizeof(a)/sizeof(a[0]); i++)
saveNum(hash_list,a[i]);
for(i = 0; i < sizeof(a)/sizeof(a[0]); i++)
printf("post:%3d --- %d ",hashFun(a[i]),getNum(hash_list,a[i]));
return 0;
}
/
4.4 叠加法
图书馆馆的图书条形码
保留3位
//打印100-999之间的水仙花数
153
1的立方 + 5的立方 + 3的立方 = 153
1 153 / 100
5 153 % 100 / 10
3 153 % 10
321432543
321 num / 1000000
432 num % 1000000 / 1000
543 num % 1000
求和
进行求和
1296 % 1000;//将这个条形码叠加之后压缩成只有三位
int hashFun(int key)//key条形码
{
int post =
}
int a[] = {321432543,654657345,234456300,213342,123453333};
#include <stdio.h>
//哈希函数
int hashFun(int key)
{
int post = (key / 1000000 + key % 1000000 / 1000 + key % 1000)%1000;
return post;
}
//存储数据
void saveNum(int *hash_list,int key)
{
int post = hashFun(key);
hash_list[post] = key;
}
//获取数据
int getNum(int *hash_list,int key)
{
int post = hashFun(key);
return hash_list[post];
}
int main(int argc, const char *argv[])
{
int a[] = {321432543,654657345,234456300,213342,123453333};
int hash_list[1000] = { 0 };//哈希函数的到的存储位置不可能大于1000
int i;
for(i = 0; i < sizeof(a)/sizeof(a[0]); i++)
saveNum(hash_list,a[i]);
for(i = 0; i < sizeof(a)/sizeof(a[0]); i++)
printf("post:%4d --- %d ",hashFun(a[i]),getNum(hash_list,a[i]));
return 0;
}
/
叠加法举例
/
#include <stdio.h>
typedef struct
{
int number;//图书条形码
char name[30];//图书的名字
}book_info_t;
//1.哈希函数,得到存储位置
int hashFun(int key)
{
int post = (key / 1000000 + key % 1000000 / 1000 + key % 1000) % 1000;
return post;
}
//2.将数据存储到哈希表中
void saveBookInfo(book_info_t *hash_list,book_info_t book)
{
//1.获取存储数据的位置
int post = hashFun(book.number);//因为条形码相当于关键字key
//2.将数据存储到哈希表中
hash_list[post] = book;
}
//3.将数据从哈希表中取出
book_info_t getBookInfo(book_info_t *hash_list,int key)
{
//1.先获取存储数据的位置
int post = hashFun(key);
//2.将数据取出
return hash_list[post];
}
int main(int argc, const char *argv[])
{
int i;
int num;//用来保存输入的条形码
book_info_t hash_list[1000] = { 0 };//因为叠加法后存储位置三位数
book_info_t temp;
//1.循环输入四组图书信息
for(i = 0; i < 4; i++)
{
printf("请您输入图书条形码和图书的名字: ");
scanf("%d %s",&temp.number,temp.name);
//将数据存储到哈希表中
saveBookInfo(hash_list,temp);
}
//2.取数据 ,查询图书信息
for(i = 0; i < 6; i++)
{
printf("请您输入要查询的条形码: ");
scanf("%d",&num);
temp = getBookInfo(hash_list,num);
printf("%d---%s ",temp.number,temp.name);
}
return 0;
}
4.5 保留余数法
见下面代码演示
数据个数为n
n = 11
哈希表的长度 m = n/a //n存储数据的个数 a的为装填因子,0.7-0.8之间最为合理
m = 11 / 0.75 == 15 0-15之间最大的指数为13
//prime 质数 为 不大于表长的质数
//保留余数法
int hashFun(int key)
{
int post = key % prime; //key % 13
return post;
}
/
4.6 开放地址法//解决哈希存储时产生的冲突
当冲突发生时,通过查找数组的一个空位,将数据填入,而不再用哈希函数得到数组下标
4.7解决冲突的方法
(1)线性探查法
#include <stdio.h>
//哈希函数
int hashFun(int key)
{
int post = key % 13;//取余13的原因是因为 选不大于哈希表长的最大质数
return post;
}
//哈希查找
int hashSearch(int *hash_list,int key)
{
int d = 1;//d 取值 1 2 3 4 5 当冲突发生的时候采用一次线性探查法
int post;//用来保存存储位置
int remnum;//用来保存余数
post = remnum = hashFun(key);
while(d < 15 && hash_list[post] != 0 && hash_list[post] != key)
{
//采用一次线性探查法
post = (remnum + d) % 15;
d++;
}
if(d >= 15)
return -1;//代表表已经溢出
return post;
//hash_list[post] == 0//意味着当前post这个位置可以存放数据,初始化哈希表所有位置全为0,代表没有存放数据
//hash_list[post] == key //意味着当前表中的key已经存在
}
//向哈希表中存储数据
void hashSave(int *hash_list, int key)
{
//先通过key获取存储位置,对key存储位置进行判断
int post = hashSearch(hash_list,key);
if(post == -1 || hash_list[post] == key)
{
printf("表溢出或key已经存在!!! ");
return;
}
//将数据存储到哈希表中
hash_list[post] = key;
}
int main(int argc, const char *argv[])
{
int i;
int a[11] = {23,34,14,38,46,16,68,15,7,31,26};
int hash_list[15] = { 0 };//哈希表长度为15 因为 数据长度n / 装填因子a 11 / 0.75,装填因子通常采用0.7-0.8之间最为合理
//将数据全部保存到哈希表中
for(i = 0; i < 11; i++)
{
hashSave(hash_list,a[i]);
}
//打印哈希表
for(i = 0; i < 15; i++)
{
printf("%d ",hash_list[i]);
}
printf(" ");
return 0;
}
///
(2)链地址法
#include <stdio.h>
#include <stdlib.h>
typedef struct node_t
{
int key;
struct node_t *next;
}link_node_t,*link_list_t;
//哈希函数
int hashFun(int key)
{
int post = key % 13;
return post;
}
link_list_t hashSearch(link_list_t *hash_list,int key)
{
link_list_t h = NULL;//用来保存无头链表的头指针
//1.先通过key调用哈希函数获取位置
int post = hashFun(key);//需要将判断key放入第条链表
h = hash_list[post];//h指向key对应存储位置的那条链表
while(h != NULL && h->key != key)//相当于遍历无头链表,同时检查key
{
h = h->next;
}
return h;
//h == NULL 说明没找到key可以进行存储
//h != NULL h->key == key 说明key已经存在
}
//存储数据
void hashSave(link_list_t *hash_list,int key)
{
int post = hashFun(key);
link_list_t pnew = NULL;//用来保存新创建的节点
link_list_t p = hashSearch(hash_list,key);
if(p == NULL)//key不存在,可以进行插入数据
{
//1.创建一个新的节点用来保存key
pnew = (link_list_t)malloc(sizeof(link_node_t));
if(NULL == pnew)
{
perror("pnew malloc failed");
return;
}
//2.将key保存到新节点中
pnew->key = key;
pnew->next = NULL;
//3.将新的节点插入到对应存储位置的链表中,将新节点每次插入无头链表头的位置
pnew->next = hash_list[post];
hash_list[post] = pnew;
}
else
{
printf("key已经存在了!!! ");
}
}
int main(int argc, const char *argv[])
{
int i;
link_list_t h = NULL;//临时保存每条链表的头
int a[11] = {23,34,14,38,46,16,68,15,7,31,26};
//hash_list是一个结构体指针数组,每一个元素都是结构体指针
link_list_t hash_list[13] = { 0 };//为什么长度是13,因为保留余数法每次%13 得到的位置在0-12之间
//将所有的key保存起来
for(i = 0; i < 11; i++)
{
hashSave(hash_list,a[i]);
}
//遍历哈希表 有13条链表
for(i = 0; i < 13; i++)//hash_list中保存的是13条无头链表的头指针
{
printf("%d:",i);
h = hash_list[i];
while(h != NULL)//相当于遍历无头链表
{
printf("%d ",h->key);
h = h->next;
}
printf(" ");
}
return 0;
}
#####作业#####
char a[] = "asdfasdlifadshjklrgeopaewrfpawedfoplhafgd"
统计找到字符串中出现次数最多的字符并统计其出现次数,打印输出
#include <stdio.h>
int hashFun(char key)
{
int post = key-'a';//下标为0的位置存的字符'a'的个数 1位置 'b'的个数
return post;
}
int main(int argc, const char *argv[])
{
int max = -1;
int i = 0;
int post;//保存存储位置
char a[] = "aaaabbbbacdddddeeemmmlzoe";
int hash_list[26] = { 0 };//长度为26,因为总共就26个字母
while(a[i] != '�')
{
post = hashFun(a[i]);
hash_list[post]++;
i++;
}
//经过上面的遍历后,已经统计出结果
for(i = 0; i < 26; i++)//max保存出现字母最多的次数
max = max < hash_list[i] ? hash_list[i] : max;
for(i = 0; i < 26; i++)
{
if(hash_list[i] == max)//只要与最多次数相同,那么就是最多的字母
{
printf("%c出现的次数是%d ",i+'a',hash_list[i]);
}
}
return 0;
}
(2)排序(稳定排序和不稳定排序)
2.1、冒泡排序
代码练习
#include<stdio.h>
#define N 10
int main(int argc, const char *argv[])
{
int st[N],i,j,temp;
for(i = 0; i < N; i++)
{
scanf("%d",&st[i]);
}
for(i = 0; i < N - 1; i++)
{
for(j = 0; j < N - 1 - i; j++)
{
if(st[j] > st[j + 1])
{
temp = st[j];
st[j] = st[j + 1];
st[j + 1] = temp;
}
}
}
for(i = 0; i < N; i++)
{
printf("%d ",st[i]);
}
2.2、选择排序
代码练习
#include<stdio.h>
#define N 5
int main(int argc, const char *argv[])
{
int st[N] = {0};
int i,j,temp,k;
for(i = 0; i < N; i++)
{
scanf("%d",&st[i]);
}
for(i = 0; i < N - 1; i++)
{
k = i;//开始的时候假设最小的元素的下标为i,对第一趟,开始假设的最小元素为第一个元素.
for(j = i+1; j < N; j++)
{
if(st[k] > st[j])//从一组数据里面找最小的,方法:先假设一个最小的
k = j;
}
if(k != i)
{
temp = st[i];
st[i] = st[k];
st[k] = temp;
}
}
for(i = 0; i < N; i++)
{
printf("%d ",st[i]);
}
return 0;
}
2.3、插值排序
代码练习
void insertSort(int *p, int n)
{
int i,j;
int temp;
for(i = 1; i < n; i++) //代表开始抓牌,因为默认手里已经有一张牌,所以i的下标 从1开始,终止下标是数组中最后一个元素,也就是最后一张牌
{ //需要将每一张牌插入到手里
for(j = i; j > 0; j--)//j == i 代表 j此时为你抓到的牌
{
if(p[j] < p[j-1]) //将抓到手里的牌与目前手里的牌进行比较,注意比较的顺序是从后往前比
{
temp = p[j];
p[j] = p[j-1];
p[j-1] = temp;
}
else
{
break;//因为手中的牌一直有序
}
}
}
2.4、快速排序
代码练习
https://blog.csdn.net/nrsc272420199/article/details/82587933
描述一下你对快排的理解;
//不稳定
#include <stdio.h>
//piovt 枢轴
int getPiovt(int *p,int low, int high)
{
int flag = p[low];//flag是镖旗
while(low < high)
{
//最开始从右向左进行扫描
while(flag <= p[high] && low < high)//只要p[high] >= flag 那么就high--
high--;
if(low < high)
{
p[low] = p[high];//将小于flag的数移动到左边
low++;//准备改变扫描的方向,从左向右进行扫描
}
while(flag >= p[low] && low < high)//只要p[low] <= flag 那么就low++
low++;
if(low < high)
{
p[high] = p[low];//将大于flag的数,移动到右边
high--;//准备改变扫描的方向,从右往左进行扫描
}
}
//将flag赋值到枢轴位置
p[low] = flag;
return low;//最后循环结束low == high 此时的位置就是枢轴位置
}
void showArray(int *p, int n)
{
int i;
//从右向左进行扫描
for(i = 0; i < n; i++)
{
printf("%d ",p[i]);
}
printf(" ");
}
//写一个递归函数,进行快排
void quickSort(int *p, int low,int high)
{
int piovt = getPiovt(p,low,high);
if(low < piovt-1)//递归快排枢轴的左侧
quickSort(p,low,piovt-1);
if(piovt+1 < high)//递归快排枢轴的右侧
quickSort(p,piovt+1,high);
}
int main(int argc, const char *argv[])
{
//快排思想:先找到枢轴的位置,枢轴左侧的数都小于等于枢轴位置数据,右侧大于等于
int a[8] = {32,2,54,6,78,23,17,76};
showArray(a,8);
quickSort(a,0,7);
printf("快速排序之后--------------- ");
showArray(a,8);
return 0;
}






 U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) SpringSecurity实现前后端分离认证授权
SpringSecurity实现前后端分离认证授权