您现在的位置是:首页 >技术杂谈 >数据结构与算法基础(王卓)(31):折半插入排序、希尔排序网站首页技术杂谈
数据结构与算法基础(王卓)(31):折半插入排序、希尔排序
目录
解释说明:(在程序实际执行的时候的算法运行逻辑顺序实际上和王卓老师网课中所讲的有所不同)
至于如何调整先后进行比较时,不同的间隔大小d的问题,这里标准答案给出的方法是:
折半插入排序
直接根据实际实例、根据草图写出如下程序:
Project 1:
void BinsertSort(SqList& L)
{
int i ,low = 1, high = i - 1;
for (i = 1; i < L.length; i++)
{
if (L.r[i].key < L.r[i - 1].key)
L.r[0] = L.r[i];
//if可以放到最高优先级
for (int mid = (low + high) / 2; high > low; mid = (low + high) / 2)
{
if (L.r[0].key < L.r[mid].key)
high = mid - 1;
else //if (L.r[0].key > L.r[mid].key)
low = mid + 1;
}
L.r[high + 1].key = L.r[0].key;
//L.r[low - 1].key = L.r[0].key;
}
}binary insert;
binary:二进制的; 仅基于两个数字的; 二元的; 由两部分组成的;
问题:缺少在插入元素之前的移动元素的操作
Project 2:(最终成品、结果)
void BinsertSort(SqList& L)
//binary insert;
//binary:二进制的; 仅基于两个数字的; 二元的; 由两部分组成的;
{
int i;
for (i = 1; i < L.length; i++)
//i表示位序
{
if (L.r[i].key < L.r[i - 1].key)
L.r[0] = L.r[i];
int low = 1, high = i - 1;
for (int mid = (low + high) / 2; high > low; mid = (low + high) / 2)
{
if (L.r[0].key < L.r[mid].key)
high = mid - 1;
else //if (L.r[0].key > L.r[mid].key)
low = mid + 1;
}
for (int j = i; j >= high + 1; j--)
L.r[j + 1].key = L.r[j].key;
L.r[high + 1].key = L.r[0].key;
//L.r[low - 1].key = L.r[0].key;
}
}希尔排序
直接根据实际实例、根据草图写出如下程序:
Project 1:(个人思路)
void ShellSort(SqList& L)
{
for (int i = 0; i <= L.length / 5; i++)
{
for (int i = 0; i <= L.length; i += 5)
{
每次都把数据存储到中序二叉树,再用中序遍历把这些元素全部都重新插回去
}
递归...
}
}标准答案:(PPT答案)
void ShellInsert(SqList& L, int d)
//distance:每次一步往后跨多远(5,3,1...)
{
int i, j;
for (i = d + 1; i < L.length; i++)
{
if (L.r[i].key < L.r[i - d].key)
//比较的诸多元素里,第二个元素大于第一个元素
{
L.r[0] = L.r[i];
for (j = i - d; //第一个元素
j > 0 && (L.r[0].key < L.r[j].key);
j -= d)
L.r[j + d] = L.r[j]; //记录后移
L.r[j + d] = L.r[0];
}
}
}
void ShellSort(SqList& L, int dlta[], int t)
//t:循环总共趟数
{
for (int k = 0; k < t; k++)
ShellInsert(L, dlta[k]);
//dlta[k]:增量(5, 3, 1...)
}解释说明:(在程序实际执行的时候的算法运行逻辑顺序实际上和王卓老师网课中所讲的有所不同)
(1):赋值阶段
i 的初值为每次比较的第二个元素
比较的诸多元素里,若第二个元素大于第一个元素:开始循环
(2):第一轮【第一次】比较
第一轮比较的第一次操作,只比较前面选中的两个元素而已:
比较第1个和第(d+1)个元素
- 把第二个元素放进哨兵
- 第一个元素覆盖第二个元素
- 再把第二个元素从哨兵里转移到第一个元素的位置
然后:j-=d; => j<0
第一轮比较结束实际上完整的这个分块的排序没有结束
但是由于实际上希尔排序和老师讲的算法思路有所偏差
所以,对于:我们把数据分成d份,共进行d轮排序的第一轮算法,就在这里先暂停终止了
然后(在第一轮的比较结束后),我们进行的操作并不是像王老师所说:
去找下一个分块筛选出的,第三个以及后续的其他元素进行比较和排序
而是暂时中止这个分块算法操作,去找我们存储在数据内部的第二个元素:
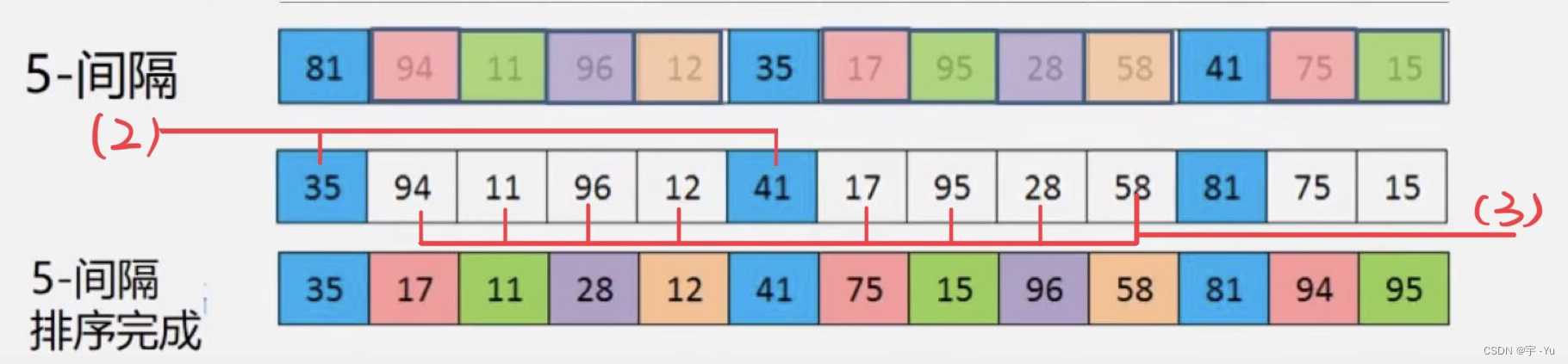
(3):第二轮到第(d)轮【第一次】比较
比较:
第2个和第(d+2)个,第3个和第(d+3)个,第4个和第(d+4)个......
直到比较到第(d)轮:第d个和第(d*2)个
现在,我们已经拥有了前2d个分门别类排序好的元素序列:
前d个元素(k:位序)
分别小于
后面的第(d+k)位元素
(4):第一轮到第(d)轮【第2次及其后续的】比较
类似(2)、(3)比较的步骤,继续往后比较,直到后续元素全部都被比较完为止:
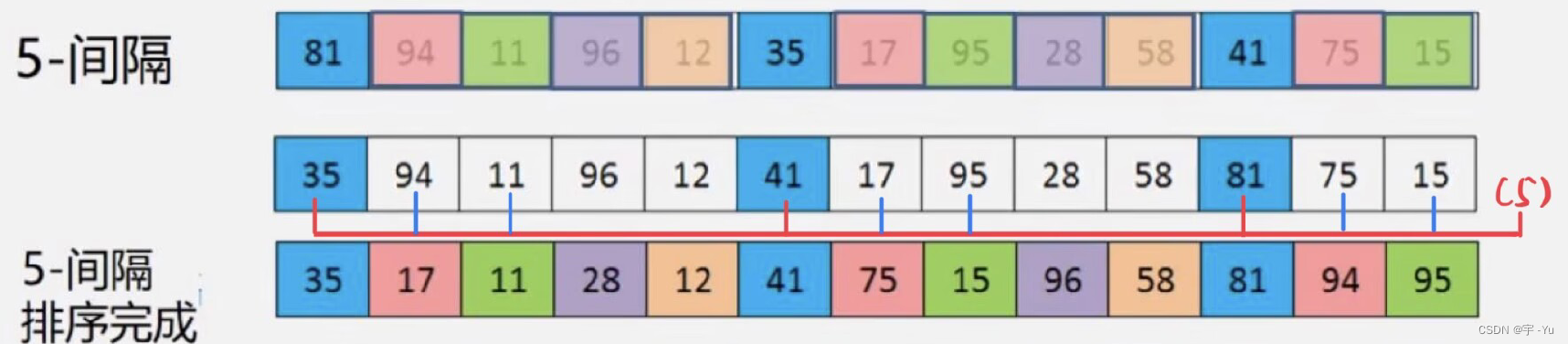
但是,这个地方(第四步)里面:
在每次比较完【通过我们定义的序列规则(每隔d个为一组)区分开来的】
里面的最后两个元素以后
我们还进行一个超越(2)、(3)步骤的操作:
对每一组的序列前面的所有元素全部都重新进行一遍遍历
也就是说:
每一组队列序列在比较完最后两个元素以后,继续向前逐个比较
如果/但凡 比较时后面的元素小于前面的元素,就把后面的元素放到前面去
重点来了:
总共比较的数据范围不止两个了以后,在每一轮每一次的比较时:每次都
继续拿【比较后较小的元素】不断和【再前面的一个序列里的元素】进行比较
由 i 新指向的元素开始,把整个该组序列前面的元素全部都比较个遍
在这个过程中,我们就完成了“排序”操作的整个/所有的流程(过程):
逐个比较
把小的元素调换到前面的位置(碰到小的往前面移)
大的元素调换到后面的位置(碰到大的往后面挪)
而在比较的数据范围不止两个了以后,每次对元素进行比较时
都把前面所有的元素都比较个遍(遍历个遍)的操作,很简单,在程序每次比较的循环里加一句:
一直向前面一个元素进行比较,直到本序列前面所有元素都被比较完毕为止
这样就完成了 :
for (j = i - d; //第一个元素
j > 0 && (L.r[0].key < L.r[j].key);
j -= d)这一段程序执行的for语句设计代码
是这整一个算法程序的运行流程的框架构建核心和精妙之处所在
至于如何调整先后进行比较时,不同的间隔大小d的问题,这里标准答案给出的方法是:
每次通过某一规则dlta[ ]
(函数?还是什么???他这里也没有给出每次的对应关系,我TM也不知道他在搞的是个什么东西)来进行某种有规律性的变化:
for (int k = 0; k < t; k++)//t:循环总共趟数
ShellInsert(L, dlta[k]); 我这里都被他整得(搞得)有点迷糊了,我也不知道他在搞什么东西
既然觉得他写的这个控制方法是一坨大便,那么我们不妨来看看这个每次都将所有数据二分的操作实例:
王道答案:
//希尔排序
void ShellSort(int A[], int n)
{
int d, i, j;
//A[0]只是暂存单元,不是哨兵,当j<=0时,插入位置已到
for (d = n / 2; d >= 1; d = d / 2)
//步长变化
for (i = d + 1; i <= n; ++i)
if (A[i] < A[i - d])
//需将A[i]插入有序增量子表
{
A[0] = A[i];
//暂存在A[0]
for (j = i - d; j > 0 && A[0] < A[j]; j -= d)
A[j + d] = A[j];
//记录后移,查找插入的位置
A[j + d] = A[0];
}//if
}根据我们设立的前置条件,按照要求进行修改:(将程序本土化)
本土化:
void ShellSort(SqList& L)
{
int i, j;
for (int d = L.length / 2; d >= 1; d = d / 2)
//步长变化
for (i = d + 1; i <= L.length; ++i)
if (L.r[i].key < L.r[i - d].key)
{
L.r[0] = L.r[i];
for (j = i - d; j > 0 && L.r[0].key < L.r[j].key; j -= d)
L.r[j + d] = L.r[j];
L.r[j + d] = L.r[0];
}//if
}这样看来,其实(实际上),程序用来控制每次不断比较的补偿d的程序,也只是需要一段:
for (int d = L.length / 2; d >= 1; d = d / 2)





 U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) Allegro16.6差分等长设置及走线总结
Allegro16.6差分等长设置及走线总结