您现在的位置是:首页 >技术杂谈 >算法套路十四——动态规划之背包问题:01背包、完全背包及各种变形网站首页技术杂谈
算法套路十四——动态规划之背包问题:01背包、完全背包及各种变形
算法套路十四——动态规划之背包问题:01背包、完全背包及各种变形
算法示例一——0/1背包:
0-1背包:有n个物品,第i个物品的体积为w[i],价值为v[i],每个物品至多选一个, 求体积和不超过capacity时的最大价值和,其中i从0开始。
动态规划递归
- 递归函数定义:
在0/1背包问题中,递归函数dfs需要2个参数,i和c来表示当前考虑的物品和背包的剩余容量,dfs(i, c)代表的是考虑前i个物品,在背包容量为c的情况下能够获得的最大价值。 - 状态转移方程:在递归过程中,我们需要依次考虑每个物品,然后采用算法套路十——回溯法之子集型回溯进行选或不选的枚举。
- 如果不选第i个物品,则为dfs(i-1, c),即前i-1个物品在背包容量为c的情况下能够获得的最大价值。
- 如果选第i个物品,则为dfs(i-1, c-w[i]) + v[i],即前i-1个物品在背包容量为c-w[i]的情况下能够获得的最大价值加上第i个物品的价值v[i]。
- 最终,dfs(i, c)的值为以上两种情况的较大值,即
转移方程为·dfs(i,c) =max (dfs(i- 1,c),dfs(i- 1,c- w[i]) + v[i])
- 边界条件:
- 当i小于0,没有物品选择,此时dfs(i, c)的值为0;或者判断当i==0时,如果背包容量c能够放下第一个物品,则直接返回第一个物品的价值v[0],否则返回0。
- 当背包的剩余容量c小于第i个物品的重量w[i]时,无法选择第i个物品,此时dfs(i, c)的值为dfs(i-1, c)。
- 所求值:dfs(n-1, capacity),表示考虑前n个物品,在背包容量为capacity的情况下能够获得的最大价值。
def zero_ one_ knapsack(capacity: int, w: List[int], v: List[int]) -> int:
n = len(w)
# python的@cache装饰器可以用来寄存函数对已处理参数的结果,以便遇到相同参数可以直接给出答案。
@cache
def dfs(i, c):
if i<0:
return 0
'''
if i==0:
return v[0] if c>=w[0] else 0
'''
if c < w[i]:
return dfs(i-1, c)
return max(dfs(i-1, c), dfs(i-1, c-w[i]) + v[i])
return dfs(n-1, capacity)
递归dfs()1:1 转换成迭代递推的dp[][]二维数组
定义一个二维数组dp,其中dp[i][j]表示考虑前i个物品,在背包容量为j的情况下能够获得的最大价值,并使用一个双重循环来遍历所有的物品和背包容量,根据0/1背包问题的状态转移方程 dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]]+v[i]) if j>=w[i] else dp[i-1][j] 来更新dp数组的值。最终,dp[n-1][capacity]的值即为所求的最大价值。
def zero_one_knapsack(capacity: int, w: List[int], v: List[int]) -> int:
n = len(w)
#n行capacity + 1列
dp = [[0] * (capacity + 1) for _ in range(n)]
for i in range(n):
for j in range(capacity + 1):
if i == 0:
dp[i][j] = v[i] if j >= w[i] else 0
else:
if j < w[i]:
dp[i][j] = dp[i - 1][j]
else:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i])
return dp[n - 1][capacity]
考虑到数组从0开始,为了数组方便我们可以将代码中所有的i加一,此时状态转移方程为状态转移方程 dp[i+1][j] = max(dp[i][j], dp[i][j - w[i]] + v[i]) if j>=w[i] else dp[i+1][j] = dp[i ][j],这样最后返回结果为dp[n][capacity],如下所示
def zero_one_knapsack(capacity: int, w: List[int], v: List[int]) -> int:
n = len(w)
#n行capacity + 1列
dp = [[0] * (capacity + 1) for _ in range(n)]
dp[0][0]=1
for i in range(n):
for j in range(capacity + 1):
#dp[i+1][j] = max(dp[i][j], dp[i][j - w[i]] + v[i]) if j>=w[i] else dp[i+1][j] = dp[i ][j]
if j < w[i]:
dp[i+1][j] = dp[i ][j]
else:
dp[i+1][j] = max(dp[i][j], dp[i][j - w[i]] + v[i])
return dp[n][capacity]
空间优化:转换为一维数组
可以将二维数组dp[]转换为一维数组dp[],此时我们需要使用一个双重循环来遍历所有的物品和背包容量,根据0/1背包问题的状态转移方程来更新dp数组的值。
其实该思路就是算法套路十——回溯法之子集型回溯中的思路二——从答案出发的思路,直接枚举所有选择物品i的情况,即枚举在所有不同容积下选择物品i的情况,并用数组记录,因此我们需要对容积从后往前遍历。
在一维数组下的状态转移方程中,f[j] 表示恰好容量为 j 时的最大或最小价值,但是它只与前 i 个物品有关。因为在状态转移时,对于当前正在考虑的第 i 件物品,假如其体积 w[i] 比当前枚举的体积 j 大,那么该物品就无法放入背包中,因此它应该不会对 f[j] 的结果产生影响。在一维数组中,我们并没有明确保存“选取了哪些物品”,而是只保存了阶段 i(前 i 个物品)和决策 j(背包容量)。在状态转移时,我们始终是以 “前i个物品” 作为暗含条件的。
def zero_one_knapsack(capacity: int, w: List[int], v: List[int]) -> int:
n = len(w)
dp = [0] * (capacity + 1)
# 遍历每个物品
for i in range(n):
# 从后往前遍历,更新 dp 数组,容量j仅仅遍历到能选择当前物品的w[i],防止数组越界
for j in range(capacity, w[i]-1, -1):
#枚举所有选择物品i的情况,并记录
dp[j] = max(dp[j], dp[j-w[i]] + v[i])
# 返回背包容量下的最大价值
return dp[capacity]
从后往前遍历的原因是为了避免在更新 dp 数组时重复使用同一个物品,且对容积j进行遍历时我们仅仅遍历到能选择当前物品的w[i]。当我们从后往前遍历时,我们确保在计算 dp[j] 时,dp[j-w[i]] 的值是基于不包含当前物品 i 的子问题的解。这样,我们可以确保每个物品只被使用一次。
如果我们从前往后遍历,那么在计算 dp[j] 时,dp[j-w[i]] 的值可能已经包含了物品 i,这样就可能导致物品 i 被重复使用,从而得到错误的结果。
如物品重量:w = [3, 4, 5] 物品价值:v = [30, 50, 60] 背包容量:capacity = 8
首先,我们看一下遍历物品 0 时从前往后遍历的情况:

从前往后遍历时,我们可以看到 dp[6] 的值为 60,这意味着我们在背包容量为 6 的情况下可以获得总价值为 60 的物品。然而,这是不正确的,因为我们实际上重复使用了物品 0(重量为 3,价值为 30)。
现在,我们看一下遍历物品 0 时从后往前遍历的情况:

从后往前遍历时,我们可以看到 dp[6] 的值为 30,这是正确的,因为我们只使用了物品 0(重量为 3,价值为 30)一次。
通过这个对比,我们可以看到从后往前遍历可以避免在更新 dp 数组时重复使用同一个物品。
算法示例二——完全背包:
完全背包:N种物品和一个容量为V的背包,每种物品都有无限件可用。第i种物品的体积是v[i],价值是val[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
0/1背包和完全背包是两种常见的背包问题,它们的主要区别在于每个物品是否可以重复使用。
在0/1背包问题中,每个物品只能使用一次,即要么选择将该物品放入背包中,要么不放入。因此,0/1背包问题也被称为“二进制背包问题”。而在完全背包问题中,每个物品可以使用多次,即可以选择将该物品放入背包中多次。因此,完全背包问题也被称为“多重背包问题”。
动态规划递归
因为每个物品可以使用多次,所以在解决完全背包问题时,我们需要对每个物品进行循环,以便计算每个物品可以使用多少次,所以在选择当前物品i之后还要继续递归是否选择当前物品i,故完全背包的状态转移方程:dp(i,j)=max(dp(i-1,j),dp(i,j-v)+val[i]),这也是与0/1背包的唯一区别,就是在选择物品i之后仍需继续递归物品i
def unbounded_knapsack(capacity: int, w: List[int], v: List[int]) -> int:
n = len(w)
# python的@cache装饰器可以用来寄存函数对已处理参数的结果,以便遇到相同参数可以直接给出答案。
@cache
def dfs(i, c):
if i<0:
return 0
'''
if i==0:
return v[0] if c>=w[0] else 0
'''
if c < w[i]:
return dfs(i-1, c)
#与0/1背包的唯一区别,dfs第一个参数仍是i
return max(dfs(i-1, c), dfs(i, c-w[i]) + v[i])
return dfs(n-1, capacity)
递归dfs()1:1 转换成迭代递推的dp[][]二维数组
同0/1背包定义一个二维数组dp,其中dp[i][j]表示考虑前i种物品,在背包容量为j的情况下能够获得的最大价值,并使用一个双重循环来遍历所有的物品和背包容量,转移方程 dp[i+1][j] = max(dp[i][j], dp[i+1][j-w[i]] + v[i]) if j>=w[i] else dp[i+1][j] = dp[i][j]来更新dp数组的值。最终,dp[n-1][capacity]的值即为所求的最大价值。
def unbounded_knapsack(capacity: int, w: List[int], v: List[int]) -> int:
n = len(w)
dp = [[0] * (capacity + 1) for _ in range(n)]
for i in range(n):
for j in range(capacity + 1):
#dp[i+1][j] = max(dp[i][j], dp[i+1][j-w[i]] + v[i]) if j>=w[i] else dp[i+1][j] = dp[i][j]
if j < w[i]:
dp[i+1][j] = dp[i][j]
else:
#与0/1背包的唯一区别,选择i+1后第一维度仍是i+1
dp[i+1][j] = max(dp[i][j], dp[i+1][j-w[i]] + v[i])
return dp[n][capacity]
空间优化:转换为一维数组
与0/1背包类似,完全背包也可以换为一维数组,不过不同的是完全背包一种物品可以选择多次,所以需要从前往后遍历。
def unbounded_knapsack(capacity: int, w: List[int], v: List[int]) -> int:
n = len(w)
dp = [0] * (capacity + 1)
for i in range(n):
for j in range(w[i], capacity + 1):
#与0/1背包的唯一区别:需要从前往后遍历
dp[j] = max(dp[j], dp[j-w[i]] + v[i])
return dp[capacity]
背包问题常见变形
- 至多装capacity,求方案数/最大价值和
- 恰好装capacity,求方案数/最大/最小价值和
- 至少装capacity,求方案数/最小价值和
最大、小值问题一般会回归到 方案数 或 数字个数问题, 一般会使用到 max/min 函数约束答案,此时使用inf 初始化来表示极端情况。 每种方式的数组初始及转移方程如何定义可参考下表,且对于每种问题为什么如此设计初始数组及转移方程经过思考相信可以理解,但做题时仍需具体问题具体分析
| 问题类型 | 二维初始数组 | 二维转移方程 | 最终结果 | 注意事项 | 一维初始数组 | 一维转移方程 |
|---|---|---|---|---|---|---|
| 求至多容量j的最大价值 | dp = [[0]*(capacity+1) for _ in range(n+1)] | dp[i+1][j] = max(dp[i][j], dp[i][j-w[i]]+v[i]) if j>=w[i] else dp[i][j] | dp[n][capacity] | 外层循环所有的物品 i,内层循环遍历所有的容量 j | f = [0] * (capacity+1) | f[j] = max(f[j], f[j-w[i]]+v[i]) |
| 求恰好为容量j的最大价值 | dp = [[-inf]*(capacity+1) for _ in range(n+1)];dp[0][0]=0 | dp[i+1][j] = max(dp[i][j], dp[i][j-w[i]]+v[i]) if j>=w[i] else dp[i][j] | dp[n][capacity] | 初始值 dp[0][0] = 0, dp[0][j] = 负无穷 (j != 0) | f = [0] + [-inf] * capacity | f[j] = max(f[j], f[j-w[i]]+v[i]) |
| 求恰好为容量j的最小价值 | dp = [[inf]*(capacity+1) for _ in range(n+1)];dp[0][0]=0 | dp[i+1][j] = min(dp[i][j], dp[i][j-w[i]]+v[i]) if j>=w[i] else dp[i][j] | dp[n][capacity] | 初始值 dp[0][0] = 0, dp[0][j] = 正无穷 (j != 0) | f = [0] + [inf] * capacity | f[j] = min(f[j], f[j-w[i]]+v[i]) |
| 求至少容量j的最小价值 | dp = [[inf]*(capacity+1) for _ in range(n+1)];dp[0][0]=0 | dp[i+1][j] = min(dp[i][j], dp[i][j-w[i]]+v[i]) if j>=w[i] else dp[i][j] | dp[n][capacity] | - | f = [0] + [inf] * capacity | f[j] = min(f[j], f[j-w[i]]+v[i]) |
| 求至多容量j的方案个数 | dp = [[1] + [0]*capacity for _ in range(n+1)] | dp[i+1][j] += dp[i][j-w[i]] if j>=w[i] else dp[i+1][j] =dp[i][j] | dp[n][capacity] | 初始值 dp[i][0] = 1 表示每个容量下至少有一种选法即选择不放任何物品 | f = [1] + [1] * capacity | f[j] += f[j-w[i]] |
| 求恰好为容量j的方案个数 | dp = [[1] + [0]*capacity for _ in range(n+1)] | dp[i+1][j] += dp[i][j-w[i]] if j>=w[i] else dp[i+1][j] =dp[i][j] | dp[n][capacity] | 初始值 dp[i][0] = 1 | f = [1] + [0] * capacity | f[j] += f[j-w[i]] |
| 求至少容量j的方案个数 | dp = [[1] + [0]*capacity for _ in range(n+1)] | dp[i+1][j] += dp[i][j-w[i]] if j>=w[i] else dp[i+1][j] =dp[i][j] | dp[n][capacity] | - | f = [1] + [0] * capacity | f[j] += f[j-w[i]] |
算法练习一:LeetCode416. 分割等和子集
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
如表格所示,求恰好容量的方案数,故二维初始数组为dp = [[1] + [0]*capacity for _ in range(n+1)],转移方程为dp[i+1][j] += dp[i][j-w[i]] if j>=w[i] else dp[i+1][j] =dp[i][j] dp[n][capacity],因此我们直接定义zero_one_knapsack_Number_of_schemes()函数来求0/1背包恰好为容量为p的方案数
动态规划
func canPartition(nums []int) bool {
s:=sum(nums)
if s%2!=0{
return false
}
p:=s/2
if zero_one_knapsack_Number_of_schemes(nums,p)==0{
return false
}
return true
}
//二维动态规划数组求恰好容量为p的0/1背包的方案数,w为体积数组
func zero_one_knapsack_Number_of_schemes(w []int,capacity int)int{
n:=len(w)
dp:=make([][]int,n+1)
for i := range dp {
dp[i] = make([]int, capacity+1)
}
dp[0][0] = 1
for i:=0;i<n;i++{
for j:=0;j<=capacity;j++{
if j<w[i]{
dp[i+1][j]=dp[i][j]
}else {
dp[i+1][j]=dp[i][j]+dp[i][j-w[i]]
}
}
}
return dp[n][capacity]
}
func sum(nums []int)int{
sum:=0
for _,x:=range nums{
sum+=x
}
return sum
}
空间优化为一维数组
一维数组初始化为f = [1] + [0] * capacity,转移方程为f[j] += f[j-w[i]],且定义zero_one_knapsack_Number_of_schemes()函数来求0/1背包恰好为容量为p的方案数
func canPartition(nums []int) bool {
s:=sum(nums)
if s%2!=0{
return false
}
p:=s/2
if one_dimensional_zero_one_knapsack_Number_of_schemes(nums,p)==0{
return false
}
return true
}
//一维动态规划数组求恰好容量为p的0/1背包的方案数
func one_dimensional_zero_one_knapsack_Number_of_schemes(w []int,capacity int)int{
n:=len(w)
dp:=make([]int,capacity +1)
dp[0]=1
for i:=0;i<n;i++{
// 从后往前遍历,更新 dp 数组,容量j仅仅遍历到能选择当前物品的w[i],防止数组越界
for j:=capacity ;j>=w[i];j--{
//枚举所有选择nums[i]的情况
dp[j]+=dp[j-w[i]]
}
}
return dp[capacity]
}
func sum(nums []int)int{
sum:=0
for _,x:=range nums{
sum+=x
}
return sum
}
算法练习二:LeetCode494. 目标和
给你一个整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 ‘+’ 或 ‘-’ ,然后串联起所有整数,可以构造一个 表达式 :
例如,nums = [2, 1] ,可以在 2 之前添加 ‘+’ ,在 1 之前添加 ‘-’ ,然后串联起来得到表达式 “+2-1” 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
本题看上去与背包问题无关,但实际为0/1背包的变形问题,我们假设数组和为sum,添加+号的数和为p,那么添加-号的和为sum-p,则有p-(sum-p)=target,则2p=target+sum,则题目的要求可以写为选择数组中的数,使其和恰好为(target+sum)/2。
动态规划
如表格所示,求恰好容量的方案数,故二维初始数组为dp = [[1] + [0]*capacity for _ in range(n+1)],转移方程为dp[i+1][j] += dp[i][j-w[i]] if j>=w[i] else dp[i+1][j] =dp[i][j] dp[n][capacity],因此我们直接调用上一题中的zero_one_knapsack_Number_of_schemes()函数来求0/1背包恰好为容量为p的方案数
//p
//s-p
//p-s+p=t
//p=(t+s)/2
//等价于和为p的方案数
func findTargetSumWays(nums []int, target int) int {
target += sum(nums)
if target<0||target%2!=0{
return 0
}
p:=target/2
return zero_one_knapsack_Number_of_schemes(nums,p)
}
//二维动态规划数组求恰好容量为p的0/1背包的方案数,w表示体积数组
func zero_one_knapsack_Number_of_schemes(w []int,capacity int)int{
n:=len(w)
dp:=make([][]int,n+1)
for i := range dp {
dp[i] = make([]int, capacity +1)
}
dp[0][0] = 1
for i:=0;i<n;i++{
for j:=0;j<=capacity ;j++{
if j<w [i]{
dp[i+1][j]=dp[i][j]
}else {
dp[i+1][j]=dp[i][j]+dp[i][j-w[i]]
}
}
}
return dp[n][capacity]
}
func sum(nums []int)int{
sum:=0
for _,x:=range nums{
sum+=x
}
return sum
}
空间优化为一维数组
一维数组初始化为f = [1] + [0] * capacity,转移方程为f[j] += f[j-w[i]],直接调用上一题中one_dimensional_zero_one_knapsack_Number_of_schemes()函数来求0/1背包恰好为容量为p的方案数
func findTargetSumWays(nums []int, target int) int {
target += sum(nums)
if target<0||target%2!=0{
return 0
}
p:=target/2
return one_dimensional_zero_one_knapsack_Number_of_schemes(nums,p)
}
//一维动态规划数组求恰好容量为p的0/1背包的方案数
func one_dimensional_zero_one_knapsack_Number_of_schemes(w []int,capacity int)int{
n:=len(w)
dp:=make([]int,capacity +1)
dp[0]=1
for i:=0;i<n;i++{
// 从后往前遍历,更新 dp 数组,容量j仅仅遍历到能选择当前物品的w[i],防止数组越界
for j:=capacity;j>=w[i];j--{
//枚举所有选择nums[i]的情况
dp[j]+=dp[j-w[i]]
}
}
return dp[capacity]
}
func sum(nums []int)int{
sum:=0
for _,x:=range nums{
sum+=x
}
return sum
}
算法练习三:LeetCode322. 零钱兑换
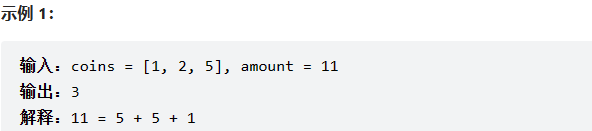
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
动态规划
该题中对于不同的硬币可以重复选择,故为完全背包问题的变形。
如表格所示,求恰好金额的最少硬币数,即恰好容量的最小价值,每个物品价值为1,故二维初始数组为dp = [[inf]*(capacity+1) for _ in range(n+1)];dp[0][0]=0,转移方程为dp[i+1][j] = min(dp[i][j], dp[i][j-w[i]]+v[i]) if j>=w[i] else dp[i][j],本题的所有v[i]都表示物品数为1,故定义unbounded_knapsack_Min_items()求恰好容量的的最少物品数。
func coinChange(coins []int, amount int) int {
ans := unbounded_knapsack_Min_items(coins,amount)
if ans < math.MaxInt/2 {
return ans
}
return -1
}
func unbounded_knapsack_Min_items(nums []int,capacity int)int{
n := len(nums)
dp:=make([][]int,n+1)
for i:=0;i<=n;i++{
dp[i]=make([]int, capacity+1)
for j := range dp[0] {
dp[i][j] = math.MaxInt / 2 // 除 2 是防止下面 + 1 溢出
}
}
dp[0][0]=0
for i:=0;i<n;i++{
for j:=0;j<=capacity;j++{
if j<nums[i]{
dp[i+1][j]=dp[i][j]
}else{
dp[i+1][j]=min(dp[i][j],dp[i+1][j-nums[i]]+1)
}
}
}
return dp[n][capacity]
}
func min(a, b int) int { if a > b { return b }; return a }
空间优化为一维数组
由表格可知数组初始化为dp = [0] + [inf] * capacity 转移方程为dp[j] = min(dp[j], dp[j-w[i]]+v[i]),本题的所有v[i]都为1,且定义one_dimensional_unbounded_knapsack_Min_items()来求一维数组下恰好容量的最少物品数
func coinChange(coins []int, amount int) int {
ans := one_dimensional_unbounded_knapsack_Min_items(coins,amount)
if ans < math.MaxInt/2 {
return ans
}
return -1
}
func one_dimensional_unbounded_knapsack_Min_items(w []int,capacity int)int{
n := len(w)
dp:=make([]int,capacity+1)
for i:=0;i<=capacity;i++{
dp[i]=math.MaxInt/2
}
dp[0]=0
for i:=0;i<n;i++{
for j:=w[i];j<=capacity;j++{
dp[j]=min(dp[j],dp[j-w[i]]+1)
}
}
return dp[capacity]
}
func min(a, b int) int { if a > b { return b }; return a }
算法练习四:LeetCode279. 完全平方数
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。1 <= n <= 104
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
动态规划
本题也是对于完全背包的变形,与上题类似,不过其中的物品体积w为1到10000所有的平凡数组成的数组,故直接调用上题的unbounded_knapsack_Min_items()求和为n的最少平方数个数
func numSquares(n int) int {
w := make([]int, 100)
for i := 0; i < len(w); i++ {
w[i] = (i+1) * (i+1)
}
return unbounded_knapsack_Min_items(w,n)
}
func unbounded_knapsack_Min_items(nums []int,capacity int)int{
n := len(nums)
dp:=make([][]int,n+1)
for i:=0;i<=n;i++{
dp[i]=make([]int, capacity+1)
for j := range dp[0] {
dp[i][j] = math.MaxInt / 2 // 除 2 是防止下面 + 1 溢出
}
}
dp[0][0]=0
for i:=0;i<n;i++{
for j:=0;j<=capacity;j++{
if j<nums[i]{
dp[i+1][j]=dp[i][j]
}else{
dp[i+1][j]=min(dp[i][j],dp[i+1][j-nums[i]]+1)
}
}
}
return dp[n][capacity]
}
func min(a, b int) int { if a > b { return b }; return a }
空间优化为一维数组
直接调用上题的one_dimensional_unbounded_knapsack_Min_items()来求一维数组下和为n的最少平方数个数
func numSquares(n int) int {
w := make([]int, 100)
for i := 0; i < len(w); i++ {
w[i] = (i+1) * (i+1)
}
return one_dimensional_unbounded_knapsack_Min_items(w,n)
}
func one_dimensional_unbounded_knapsack_Min_items(w []int,capacity int)int{
n := len(w)
dp:=make([]int,capacity+1)
for i:=0;i<=capacity;i++{
dp[i]=math.MaxInt/2
}
dp[0]=0
for i:=0;i<n;i++{
for j:=w[i];j<=capacity;j++{
dp[j]=min(dp[j],dp[j-w[i]]+1)
}
}
return dp[capacity]
}
func min(a, b int) int { if a > b { return b }; return a }
算法练习五:LeetCode518. 零钱兑换 II
给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。
假设每一种面额的硬币有无限个。
题目数据保证结果符合 32 位带符号整数。
动态规划
本题求和为amount的方案数,可以直接修改练习一中的zero_one_knapsack_Number_of_schemes()为unbounded_knapsack_Number_of_schemes()来解决,且由示例可知,0/1背包改为完全背包仅需在选择物品i之后仍继续递归物品i即可
func change(amount int, coins []int) int {
return unbounded_knapsack_Number_of_schemes(coins,amount)
}
//二维动态规划数组求恰好容量为p的完全背包的方案数,w为体积数组
func unbounded_knapsack_Number_of_schemes(w []int,capacity int)int{
n:=len(w)
dp:=make([][]int,n+1)
for i := range dp {
dp[i] = make([]int, capacity+1)
}
dp[0][0] = 1
for i:=0;i<n;i++{
for j:=0;j<=capacity;j++{
if j<w[i]{
dp[i+1][j]=dp[i][j]
}else {
//唯一区别
dp[i+1][j]=dp[i][j]+dp[i+1][j-w[i]]
}
}
}
return dp[n][capacity]
}
func sum(nums []int)int{
sum:=0
for _,x:=range nums{
sum+=x
}
return sum
}
空间优化为一维数组
直接修改练习一中的one_dimensional_zero_one_knapsack_Number_of_schemes()为one_dimensional_unbounded_knapsack_Number_of_schemes()来解决,且由示例可知,0/1背包改为完全背包在用一维数组解决时只需要将遍历循序由从后往前修改为从前往后遍历即可。
func change(amount int, coins []int) int {
return one_dimensional_unbounded_knapsack_Number_of_schemes(coins,amount)
}
//一维动态规划数组求恰好容量为p的0/1背包的方案数
func one_dimensional_unbounded_knapsack_Number_of_schemes(w []int,capacity int)int{
n:=len(w)
dp:=make([]int,capacity +1)
dp[0]=1
for i:=0;i<n;i++{
// 从后往前遍历,更新 dp 数组,容量j仅仅遍历到能选择当前物品的w[i],防止数组越界
for j:=w[i] ;j<=capacity;j++{
//枚举所有选择nums[i]的情况
dp[j]+=dp[j-w[i]]
}
}
return dp[capacity]
}
func sum(nums []int)int{
sum:=0
for _,x:=range nums{
sum+=x
}
return sum
}










 U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) Allegro16.6差分等长设置及走线总结
Allegro16.6差分等长设置及走线总结