数组、链表专题网站首页 学无止境

数组、链表专题

香农派我最爱 2023-07-01 04:00:02

简介数组、链表专题

数组、链表专题

前缀和数组
差分数组

不要纠结，干就完事了，熟练度很重要！！！多练习，多总结！！！

前缀和数组

LeetCode 303. 区域和检索 - 数组不可变

在这里插入图片描述

解题思路

核心思路是我们 new 一个新的数组preSum出来，preSum[i]记录nums[0…i-1]的累加和，看图 10 = 3 + 5 + 2：
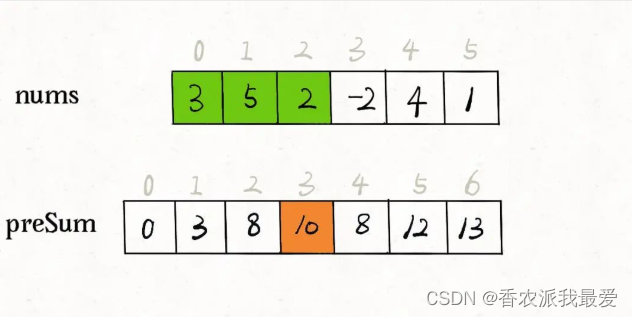
在这里插入图片描述
看这个preSum数组，如果我想求索引区间[1, 4]内的所有元素之和，就可以通过preSum[5] - preSum[1]得出。
这样，sumRange函数仅仅需要做一次减法运算，避免了每次进行 for 循环调用，最坏时间复杂度为常数O(1)。

代码实现

class NumArray {

    int[] preSum;
    public NumArray(int[] nums) {
        preSum = new int[nums.length +1];

        for(int i = 1;i < preSum.length;i++){
            preSum[i] = preSum[i-1]+nums[i-1];
        }
    }
    
    public int sumRange(int left, int right) {
        return preSum[right+1]-preSum[left];
    }
}

LeetCode 304. 二维区域和检索 - 矩阵不可变

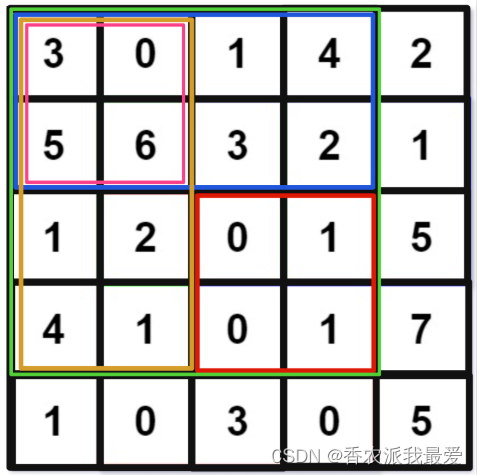
在这里插入图片描述

解题思路

在这里插入图片描述
如果我想计算红色的这个子矩阵的元素之和，可以用绿色矩阵减去蓝色矩阵减去橙色矩阵最后加上粉色矩阵，而绿蓝橙粉这四个矩阵有一个共同的特点，就是左上角就是(0, 0)原点。

那么我们可以维护一个二维preSum数组，专门记录以原点为顶点的矩阵的元素之和，就可以用几次加减运算算出任何一个子矩阵的元素和。

代码实现

class NumMatrix {
    int[][] preSum;

    public NumMatrix(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        preSum = new int[m+1][n+1];

        for(int i = 1;i <= m;i++){
            for(int j = 1;j <= n;j++){
                preSum[i][j] = preSum[i-1][j]+preSum[i][j-1]+matrix[i-1][j-1]-preSum[i-1][j-1];
            }
        }
    }
    
    public int sumRegion(int row1, int col1, int row2, int col2) {
        return preSum[row2+1][col2+1]-preSum[row2+1][col1]-preSum[row1][col2+1]+preSum[row1][col1];
    }
}

LeetCode 560. 和为 K 的子数组

在这里插入图片描述

解题思路

nt subarraySum(int[] nums, int k) {
    int n = nums.length;
    // 构造前缀和
    int[] preSum = new int[n + 1];
    preSum[0] = 0; 
    for (int i = 0; i < n; i++)
        preSum[i + 1] = preSum[i] + nums[i];

    int res = 0;
    // 穷举所有子数组
    for (int i = 1; i <= n; i++)
        for (int j = 0; j < i; j++)
            // 子数组 nums[j..i-1] 的元素和
            if (preSum[i] - preSum[j] == k)
                res++;

    return res;
}

这个解法的时间复杂度O(N^2)空间复杂度O(N)，并不是最优的解法。不过通过这个解法理解了前缀和数组的工作原理之后，可以使用一些巧妙的办法把时间复杂度进一步降低。
第二层 for 循环在干嘛呢？翻译一下就是，在计算，有几个j能够使得preSum[i]和preSum[j]的差为k。毎找到一个这样的j，就把结果加一。
我直接记录下有几个preSum[j]和preSum[i] - k相等，直接更新结果，就避免了内层的 for 循环。我们可以用哈希表，在记录前缀和的同时记录该前缀和出现的次数。

代码实现

class Solution {
    public int subarraySum(int[] nums, int k) {
        Map<Integer, Integer> preSum = new HashMap<>();
        int res = 0, sum_i = 0;
        preSum.put(0, 1);
        for(int i = 0;i < nums.length;i++){
            sum_i +=nums[i];
            int sum_j = sum_i-k;
            if(preSum.containsKey(sum_j)){
                res+=preSum.get(sum_j);
            }
            preSum.put(sum_i, preSum.getOrDefault(sum_i, 0)+1);
        }
        return res;
    }
}

差分数组

差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减。
我给你输入一个数组nums，然后又要求给区间nums[2…6]全部加 1，再给nums[3…9]全部减 3，再给nums[0…4]全部加 2，再给…
类似前缀和技巧构造的prefix数组，我们先对nums数组构造一个diff差分数组，diff[i]就是nums[i]和nums[i-1]之差：
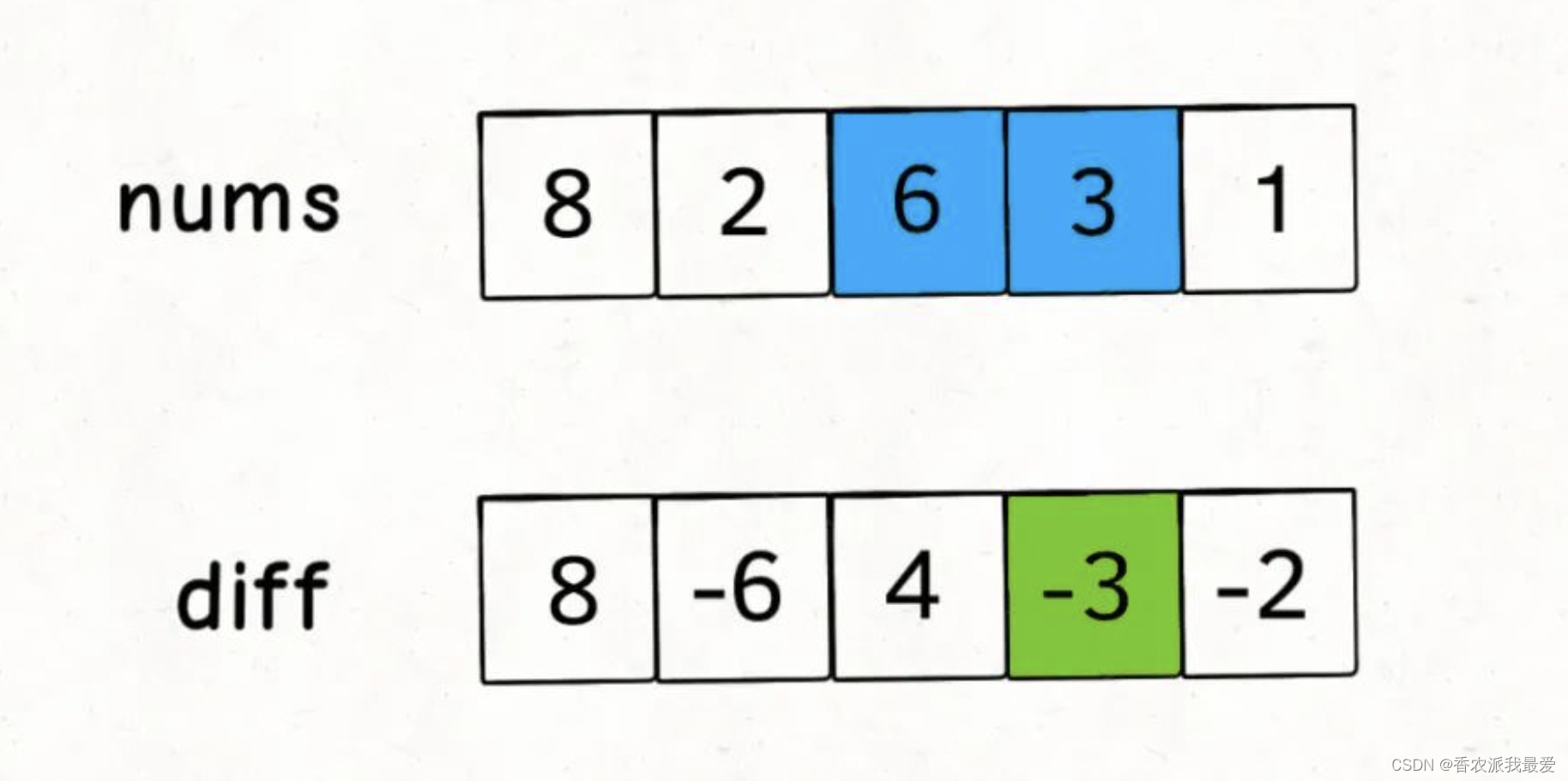
在这里插入图片描述

int[] res = new int[diff.length];
// 根据差分数组构造结果数组
res[0] = diff[0];
for (int i = 1; i < diff.length; i++) {
    res[i] = res[i - 1] + diff[i];
}

这样构造差分数组diff，就可以快速进行区间增减的操作，如果你想对区间nums[i…j]的元素全部加 3，那么只需要让diff[i] += 3，然后再让diff[j+1] -= 3即可。

只要花费 O(1) 的时间修改diff数组，就相当于给nums的整个区间做了修改。多次修改diff，然后通过diff数组反推，即可得到nums修改后的结果。

// 差分数组工具类
class Difference {
    // 差分数组
    private int[] diff;

    /* 输入一个初始数组，区间操作将在这个数组上进行 */
    public Difference(int[] nums) {
        assert nums.length > 0;
        diff = new int[nums.length];
        // 根据初始数组构造差分数组
        diff[0] = nums[0];
        for (int i = 1; i < nums.length; i++) {
            diff[i] = nums[i] - nums[i - 1];
        }
    }

    /* 给闭区间 [i,j] 增加 val（可以是负数）*/
    public void increment(int i, int j, int val) {
        diff[i] += val;
        if (j + 1 < diff.length) {
            diff[j + 1] -= val;
        }
    }

    /* 返回结果数组 */
    public int[] result() {
        int[] res = new int[diff.length];
        // 根据差分数组构造结果数组
        res[0] = diff[0];
        for (int i = 1; i < diff.length; i++) {
            res[i] = res[i - 1] + diff[i];
        }
        return res;
    }
}

public void increment(int i, int j, int val) {
    diff[i] += val;
    if (j + 1 < diff.length) {
        diff[j + 1] -= val;
    }
}

当j+1 >= diff.length时，说明是对nums[i]及以后的整个数组都进行修改，那么就不需要再给diff数组减val了。

LeetCode 303. 区域和检索 - 数组不可变

在这里插入图片描述

解题思路

代码实现

class NumArray {

    int[] preSum;
    public NumArray(int[] nums) {
        preSum = new int[nums.length +1];

        for(int i = 1;i < preSum.length;i++){
            preSum[i] = preSum[i-1]+nums[i-1];
        }
    }
    
    public int sumRange(int left, int right) {
        return preSum[right+1]-preSum[left];
    }
}