深度学习模型的可解释性有助于增加对模型预测的信任， 提高模型对与公平、隐私和其他安全挑战相关的关键决策应用程序的透明度，并且可以让我们了解网络特征，以便在将模型部署到现实世界之前识别和纠正模型所犯错误的系统模式。

图在现实世界中无处不在，代表社交网络、引用网络、化学分子、金融数据等。图神经网络 (GNN) 是一个强大的框架，用于对图相关数据进行机器学习，例如节点分类、图分类、和链接预测。

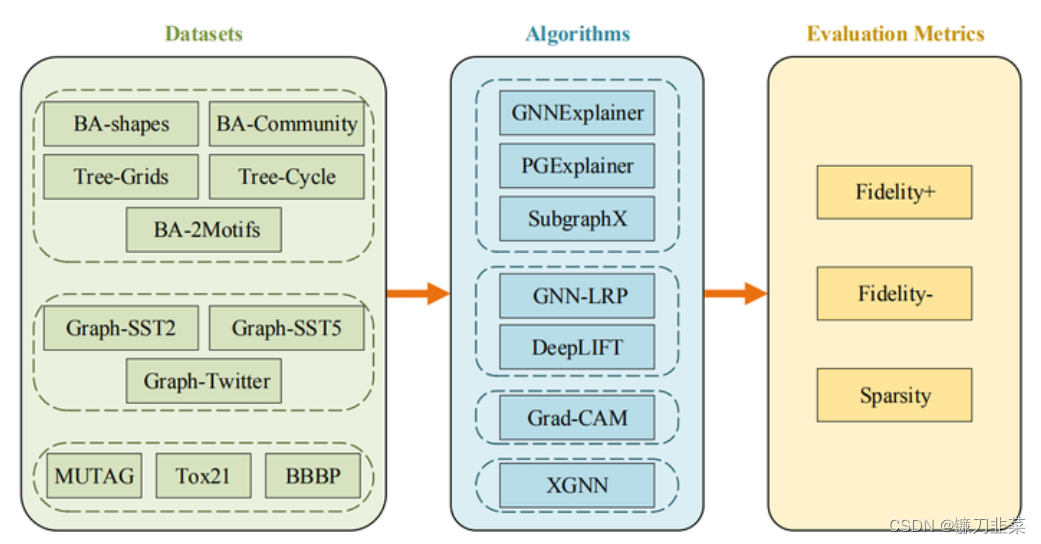
因此，本文结合论文《GNNExplainer: Generating Explanations for Graph Neural Networks》探讨以下5个方面：

• GNN 需要可解释性
• 解释 GNN 预测的挑战
• 不同的 GNN 解释方法
• GNNExplainer的直观解释
• 使用 GNNExplainer 解释节点分类和图分类的实现

GNNExplainer

GNNExplainer 是一种与模型无关的基于扰动的方法，可以为任何基于图的机器学习任务上的任何基于 GNN 的模型的预测提供可解释的报告。GNNExplainer学习边和节点特征的软掩码，然后通过掩码的优化来解释预测。GNNExplainer会获取输入图并识别紧凑的子图结构和在预测中起关键作用的一小部分节点特征。

论文摘要：图神经网络（GNN）是在图上进行机器学习的强大工具。GNN通过沿着输入图的边递归地传递神经消息，将节点特征信息与图结构相结合。然而，结合图结构和特征信息会导致复杂的模型，并且解释GNN做出的预测仍然没有解决。在这里，我们提出了GNNExplainer，这是第一种通用的、模型不可知的方法，用于在任何基于图的机器学习任务上为任何基于GNN的模型的预测提供可解释的解释。给定一个例子，GNNExplainer确定了一个紧凑的子图结构和一小部分节点特征，这些特征在GNN的预测中起着至关重要的作用。此外，GNNExplainer可以为整个实例类生成一致且简洁的解释。我们将GNNExplainer公式化为一个优化任务，该任务使GNN的预测和可能的子图结构的分布之间的相互信息最大化。在合成图和真实世界图上的实验表明，我们的方法可以识别重要的图结构和节点特征，并且平均比基线高17.1%。GNNExplainer提供了各种好处，从可视化语义相关结构的能力到可解释性，再到深入了解错误GNN的错误。

论文地址：https://arxiv.org/abs/1903.03894?context=cs
代码地址：https://github.com/RexYing/gnn-model-explainer

Introduction

图神经网络(Graph Neural Network), 作为深度学习领域最热门的方向之一,相关论文在各大顶会层出不穷. 但是，图神经网络的解释性问题没有得到较多的关注.图神经网络的解释性是非常有必要的:(1) 提升了GNN的可信程度. (2) 在一些注重公平性,隐私性和安全性的决策应用,可以提升决策的透明度. (3)可以更好的理解图本身的特性.

虽然一些基于Attention机制的模型(如Graph Attention Network)可以一定程度上对GNN进行解释. 但是,作者认为它们有两个问题: (1)GAT可以学习节点之间关系的权重,但是其只能实现对结构的进行解释而无法通过特征的角度进行解释. (2) 节点的1-hop邻居和2-hop邻居可能有重叠,GAT会学习到同一对节点之间的不同权重.这时候到底该用那个无法抉择.

因此, 本文提出了GNNExplainer可以从网络结构和节点属性的角度来对任意图神经网络和任意图挖掘任务生成解释. GNNExplainer旨在探寻与预测结果最相关的子图结构来实现对结果的解释,其中Graph Mask和Feature Mask可以分别对实现对结构和特征的筛选.

常规解释其他神经网络的两个主流方式是：

1. 对于模型本身进行解释。
2. 通过对指标重要性的解释来解释模型。

但这两种解释方案，都没有把关系信息考虑进解释方案中。因此提出GNNExplainer，此方法将一个已经训练好的GNN和其预测结果作为输入，然后通过输出一个子图以及该子图上更少的特征，表示其输出最大程度的影响了该GNN的预测结果。这个子图可以最大化与GNN预测结果的互信息。在这个过程中，会有一个图掩码，用于挑选真正重要的子图；一个特征掩码，用于挑选真正重要的子特征集。用一个图解释一下这个过程，如下：

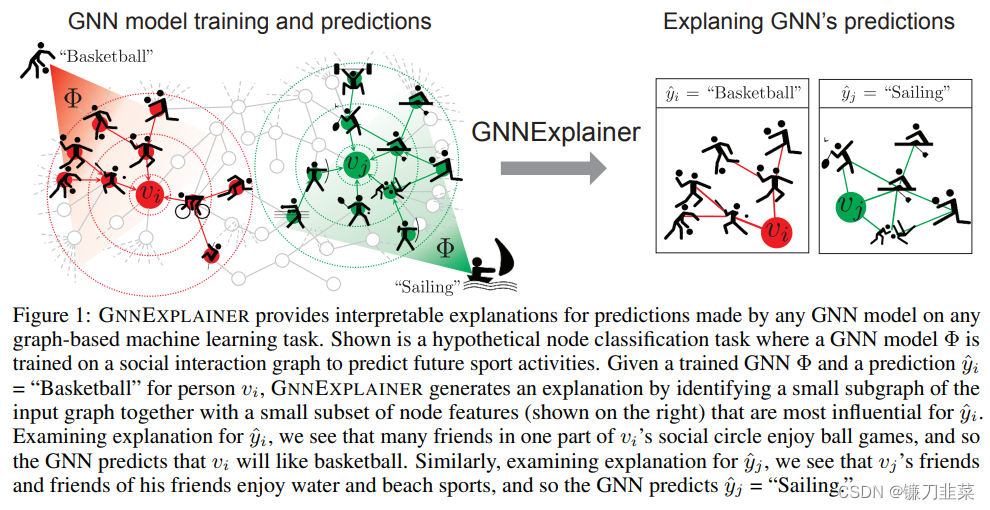
上图给了一个如何对GNN预测的节点分类(Basketball和Sailing)的结果进行解释.针对节点 $v_i$ 及其label篮球，其邻居中很多人都喜欢球类也有一些喜欢非球类, GNNExplainer可以自动的找到邻居中都喜欢球类的这些人. 同样的,针对节点 $v_j$ ,GNNExplainer也可以发现其好友中同样喜欢水上/沙滩类运动的好友.

Model

GNNExplainer通过生成传递关键语义的掩码来捕获重要的输入特征，从而产生与原始预测相似的预测。它学习边和节点特征的软掩码，通过掩码优化来解释预测。以不同方式为输入图获得掩码可以获得重要的输入特征。还根据预测任务的类型生成不同的掩码，例如节点掩码、边掩码和节点特征掩码。

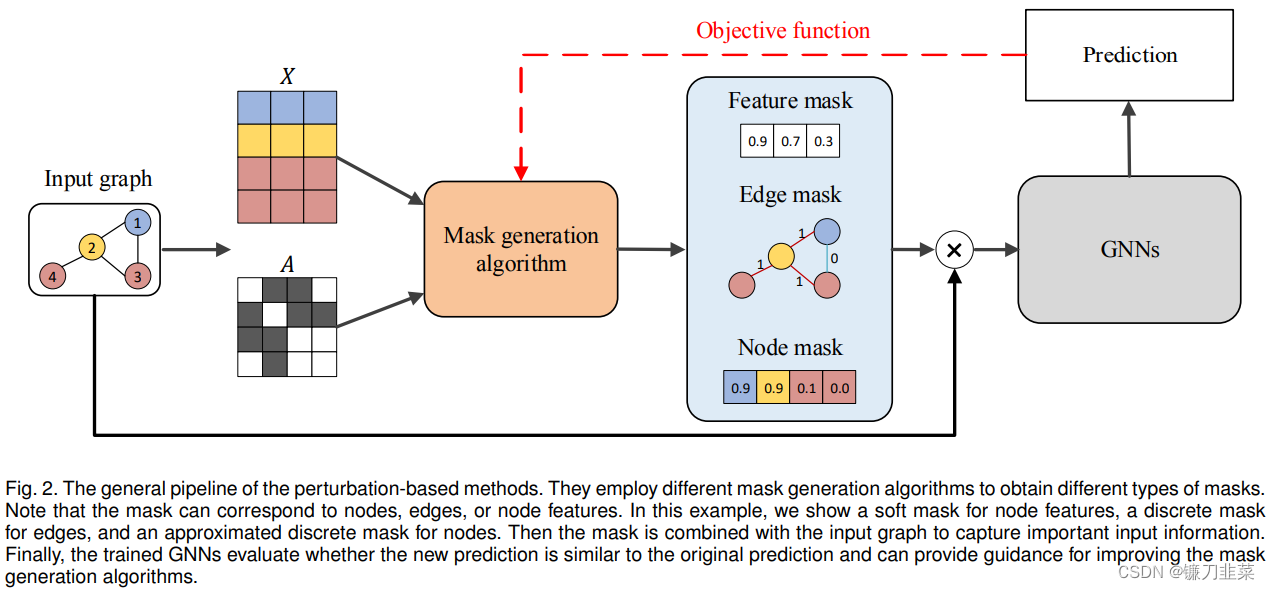
生成的掩码与输入图相结合，通过逐元素乘法获得包含重要输入信息的新图。最后，将新图输入经过训练的 GNN 以评估掩码并更新掩码生成算法。

作者首先归纳了GNN的三个步骤: (1)MSG, 构建节点之间需要传递的消息. (2)AGG,收集节点相关的消息. (3)UPDATE, 更新节点表示。下图解释了GNNExplainer要做的事情：自动发现重要的消息和特征。

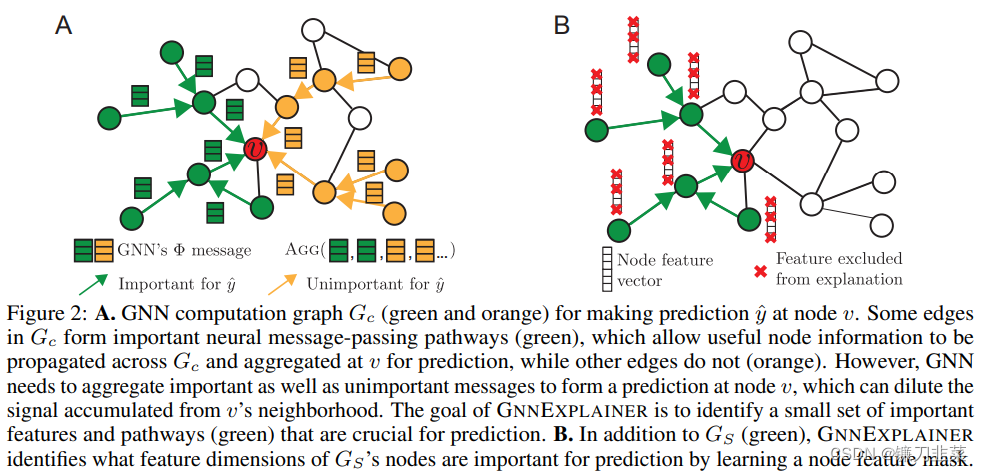
图$G=(V,E)$为要分析的图，$E$为边集合，$V$为结点集合，并且有一个d维的节点特征集合$X=x_1,...,x_n,x_i\in {\mathbb{R}}^d$。其中结点个数为$n$。$f$为映射函数 f : V → { 1 , . . . , C } f:V ightarrow {1,...,C} f:V→{1,...,C}将图中每个结点分类为$C$类中的一类。GNN模型$\Phi$用来近似函数$f$的分类功能。
通常，在模型的第$l$层，我们认为一个GNN模型，由以下三个核心部分组成：

1. MSG，代表每对节点间的信息传递部分。在一对节点$(v_i,v_j)$中的信息，可以通过两个节点在上一层的编码$h_i^{l-1},h_j^{l-1}$表示$m_{ij}^l=MSG(h_i^{l-1},h_j^{l-1},r_{ij})$。
2. AGG，表示对于某个节点中心子图的信息汇集。假定节点$v_i$的邻居节点集合为$N_{v_i}$，那么其信息汇聚可以表示为$M_i^l=AGG(M_{ij}^l|v_j\in N_{v_i})$。
3. UPDATE，表示根据上面内容，进行编码更新。可以表示为$h_j^l=UPDATE(M_i^l,h_i^{l-1})$。

那么模型要做的事情，就是通过GNN给定的预测结果$\hat{y}$,找到其解释$(G_S,X_S^F)$ ，其中前者是重要的子图结构，后者是重要的特征子集。PS: 这里的$F$表示掩码，即$X_S^F=x_j^F|v_j\in G_S$。

Single-instance explanations（Explanation via Structural Information）

给定一个节点$v$，我们的目标是识别一个子图$G_S\subseteq G_c$和相关的特征 X S = { x j ∣ v j ∈ G S } X_S={x_j|v_jin G_S} XS​={xj​∣vj​∈GS​}，它们对于GNN的预测结果$\hat{y}$是非常重要的。现在，假设$X_S$是d维节点特征的一个小的子集；我们稍后讨论如何自动确定节点特征的哪些维度需要包括在解释中。我们使用互信息$MI$形式化了重要性的概念，并将GNNEXPLAINER公式化为以下优化框架：$$\underset{G_S}{\max }MI(Y,(G_S,X_S))=H(Y)-H(Y|G=G_S,X=X_S)\text{\hspace{1em}(1)}$$
对于节点$v$，MI量化了预测$\hat{y}=\Phi (G_c,X_c)$的概率的变化，当$v$的计算图受限于解释的子图$G_S$，以及它的节点特征受限于$X_S$。

上式中的, 熵$H(Y)$是常数，因为GNNExplainer是在训练好的GNN上模型上进行解释，也就是$\Phi$是固定的。最大化预测的标签分布$Y$与解释$(G_S,X_S)$等价于最小化条件熵 $H\left(Y|G=G_S,X=X_S\right)$ :$$H\left(Y|G=G_S,X=X_S\right)=-{\mathbb{E}}_{Y|G_S,X_S}[\log P_{\Phi }(Y|G=G_S,X=X_S)]\text{\hspace{1em}(2)}$$

GNNEXPLAINER’s optimization framework。直接优化GNNEXPLAINER的目标是不易处理的，因为$G_c$具有指数级多个子图$G_S$，这些子图是$\hat{y}$的候选解释。因此，我们考虑一个子图$G_S$的分数邻接矩阵，即$A_S\in [0,1{]}^{n\times n}$，并且强制子图约束：$A_S[j,k]\le A_c[j,k]\text{ for all }j,k$。这种连续的放松可以解释为$G_c$的子图的分布的一种变分近似。实际上，如果我们将$G_S\sim \mathcal{G}$视为一个随机图变量，那么等式2可以变为：$$\underset{\mathcal{G}}{\min }{\mathbb{E}}_{G_S\sim \mathcal{G}}H(Y|G=G_S,X=X_S)\text{\hspace{1em}(3)}$$
利用Jensen不等式和凸性假设,我们可以得到$$\underset{\mathcal{G}}{\min }H(Y|G={\mathbb{E}}_{\mathcal{G}}[G_S],X=X_S)\text{\hspace{1em}(4)}$$
在实际应用中，由于神经网络的复杂性，凸性假设不成立。然而，在实验中，我们发现使用正则化将这个目标最小化通常会导致与高质量解释相对应的局部最小值。

为了实现对${\mathbb{E}}_{\mathcal{G}}$的估计，这里用来平均场变分近似对$\mathcal{G}$进行分解为一个多元伯努利分布$P_{\mathcal{G}}(G_S)={\prod }_{(j,k)\in G_c}{A}_S[j,k]$。这里$A_S[j,k]$代表边$(v_j,v_k)$存在的期望。上式中的${\mathbb{E}}_{\mathcal{G}}$可以用$A_c\odot \sigma (M)$来代替，这里$M$是就是我们要学习的Graph Mask。

很多任务只关心部分类的节点及其模型如何对该类进行预测。因此上式可以修正为：$$\underset{M}{\min }-\sum _{c=1}^{C}1[y=c]\log P_{\Phi }(Y=y|G=A_c\odot \sigma (M),X=X_c)\text{\hspace{1em}(5)}$$在实际解释的时候，只需要设定阈值将$M$中的部分低于阈值的边移除就好，这样就从结构的角度实现了对模型的解释。

Joint learning of graph structural and node feature information（Explanation via Feature Information）

与结构方面的解释类似，这里通过选择与预测结果最相关的部分特征来实现对模型的解释。 X S F = { x j F ∣ v j ∈ G S } , x j F = [ x j , t 1 , . . . , x j , t k ]  for  F t i = 1 (6) ag{6} X_S^F={x_j^F|v_jin G_S}, x_j^F=[x_{j,t_1},...,x_{j,t_k}] ext{ for } F_{t_i}=1 XSF​={xjF​∣vj​∈GS​},xjF​=[xj,t1​​,...,xj,tk​​] for Fti​​=1(6)这里的特征选择器 F ∈ { 0 , 1 } d F in{0,1}^{d} F∈{0,1}d可以将部分无关特征移除。联合考虑结构和特征的选择，本文最终的优化目标为：$$\underset{G_S,F}{\max }MI(Y,(G_S,F))=H(Y)-H(Y|G=G_S,X=X_S^F)\text{\hspace{1em}(7)}$$其中$X_S^F=X_S\odot F$。这里作者利用了重采样技术 $X=Z+(X_s-Z)\odot F$ 来优化模型。

Integrating additional constraints into explanations.(将额外的约束整合到解释中)。 为了对解释施加更多的属性，我们可以使用正则化项在等式 (7) 中扩展GNNEXPLAINER的目标函数。 例如，我们使用逐元素熵来鼓励结构和节点特征掩码是离散的。 此外，GNNEXPLAINER 可以通过拉格朗日约束乘数或附加正则化项等技术对特定领域的约束进行编码。 我们包括许多正则化项以产生具有所需属性的解释。 我们通过添加掩码参数的所有元素的总和作为正则化项来惩罚大尺寸的解释。

重要的是，GNNEXPLAINER 自动提供代表有效计算图的解释，因为它优化了整个计算图的结构掩码。 即使断开连接的边对于神经消息传递很重要，也不会选择它进行解释，因为它不会影响 GNN 的预测。 实际上，这意味着解释$G_S$ 倾向于是一个小的连通子图。

Multi-instance explanations through graph prototypes

上面都是对单个节点进行解释，但是很多时候我们更关注：如何对一类节点的预测进行解释? 本文把这个叫做multi-instance explanations,其主要包含两步

• 给定节点类别$c$ , 作者通过对该类的所有节点的Embedding进行平均得到了参考节点$v_c$ .然后将之前针对单节点解释的优化目标换成 $G_S(v_c)$ .
• 聚集邻居矩阵得到Graph Prototype $A_{proto}$ ,即:同类节点之间共享的图模式.

GNNExplainer model extensions

Any machine learning task on graphs

除了结点预测，GNNExplainer还可以解释针对边预测和图预测的任务。

Any GNN model

GNNExplainer可以应用于（不限于）如下图模型

• Graph Convolutional Networks
• Gated Graph Sequence Neural Networks
• Jumping Knowledge Networks
• Graph attention networks
• Line-Graph NNs
• Position-aware GNN

名词解释

Explainability versus Interpretability
在一些研究中，“explainability” 和 “interpretability”被交替使用。作者认为这两个术语应该被区分开来，遵循论文[44]来区分这两个术语。如果一个模型本身能够对其预测提供人类可理解的解释，则认为这个模型是 “interpretable”。注意，这样的模型在某种程度上不再是一个黑盒子。例如，一个决策树模型就是一个 "interpretable“的模型。同时，"explainable "模型意味着该模型仍然是一个黑盒子，其预测有可能被一些事后解释技术所理解。

使用GNNExplainer对node的解释代码

本文使用的是pytorch-geometric实现的GNNExplainer作为示例。

explain_node()学习并返回一个节点特征掩码和一个边缘掩码，它们在解释 GNN 对节点分类所做的预测中起着至关重要的作用。

#!/usr/bin/env python
# encoding: utf-8
# Created by BIT09 at 2023/4/26
import matplotlib.pyplot as plt
import torch
import torch.nn.functional as F
from torch_geometric.datasets import Planetoid
from torch_geometric.loader import NeighborLoader
from torch_geometric.nn import GCNConv, GNNExplainer


# Define the GCN model
class Net(torch.nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = GCNConv(dataset.num_features, 16, normalize=False)
        self.conv2 = GCNConv(16, dataset.num_classes, normalize=False)
        self.optimizer = torch.optim.Adam(self.parameters(), lr=0.02, weight_decay=5e-4)

    def forward(self, x, edge_index):
        x = F.relu(self.conv1(x, edge_index))
        x = F.dropout(x, training=self.training)
        x = self.conv2(x, edge_index)
        return F.log_softmax(x, dim=1)


def accuracy(pred_y, y):
    """Calculate accuracy"""
    return ((pred_y == y).sum() / len(y)).item()


# define the function to Train the model
def train_nn(model, x, edge_index, epochs, device):
    criterion = torch.nn.CrossEntropyLoss()
    optimizer = model.optimizer

    model.train()
    for epoch in range(epochs + 1):
        total_loss = 0
        acc = 0
        val_loss = 0
        val_acc = 0

        # Train on batches
        for batch in train_loader:
            optimizer.zero_grad()
            batch = batch.to(device)
            out = model(batch.x, batch.edge_index)
            loss = criterion(out[batch.train_mask], batch.y[batch.train_mask])

            total_loss += loss
            acc += accuracy(out[batch.train_mask].argmax(dim=1),
                            batch.y[batch.train_mask])
            loss.backward()
            optimizer.step()

            # Validation
            val_loss += criterion(out[batch.val_mask], batch.y[batch.val_mask])
            val_acc += accuracy(out[batch.val_mask].argmax(dim=1), batch.y[batch.val_mask])

        # Print metrics every 10 epochs
        if epoch % 10 == 0:
            print(f'Epoch {epoch:>3} | Train Loss: {total_loss / len(train_loader):.3f} '
                  f'| Train Acc: {acc / len(train_loader) * 100:>6.2f}% | Val Loss: '
                  f'{val_loss / len(train_loader):.2f} | Val Acc: '
                  f'{val_acc / len(train_loader) * 100:.2f}%')


# define the function to Test the model
def Test(model, data, device):
    """Evaluate the model on test set and print the accuracy score."""
    model.eval()
    data = data.to(device)
    out = model(data.x, data.edge_index)
    acc = accuracy(out.argmax(dim=1)[data.test_mask], data.y[data.test_mask])
    return acc


if __name__ == '__main__':
    # Load the Planetoid dataset
    dataset = Planetoid(root='../', name='Pubmed')
    data = dataset[0]
    # Set the device dynamically
    print(torch.cuda.is_available())
    device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')

    # Create batches with neighbor sampling
    train_loader = NeighborLoader(data, num_neighbors=[5, 10], batch_size=16, input_nodes=data.train_mask)
    model = Net().to(device)

    # Train the model
    train_nn(model, x=data.x, edge_index=data.edge_index, epochs=200, device=device)

    # Test
    acc = Test(model, data, device=device)
    print(f'
GCN test accuracy: {acc * 100:.2f}%
')

    # Explain the GCN for node
    node_idx = 20
    x, edge_index = data.x, data.edge_index
    # Pass the model to explain to GNNExplainer
    explainer = GNNExplainer(model, epochs=100, return_type='log_prob')
    # returns a node feature mask and an edge mask that play a crucial role to explain the prediction made by the GNN for node 20
    node_feat_mask, edge_mask = explainer.explain_node(node_idx, x, edge_index)
    ax, G = explainer.visualize_subgraph(node_idx, edge_index, edge_mask, y=data.y)
    plt.show()
    print("Ground Truth label for node: ", node_idx, " is ", data.y.cpu().numpy()[node_idx])
    out = torch.softmax(model(data.x, data.edge_index), dim=1).argmax(dim=1)
    print("Prediction for node ", node_idx, "is ", out[node_idx].cpu().detach().numpy().squeeze())

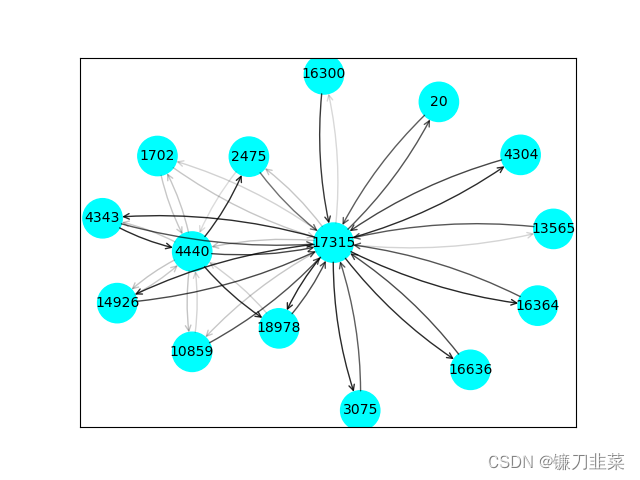
使用GNNExplainer对graph的解释代码

Explain_graph()用于图分类；它学习并返回一个节点特征掩码和一个边掩码，这两个掩码在解释GNN对一个图的预测时起着至关重要的作用。

#!/usr/bin/env python
# encoding: utf-8
# Created by BIT09 at 2023/4/27
import matplotlib.pyplot as plt
import torch
import torch.nn.functional as F
from torch.nn import Linear
from torch_geometric.datasets import TUDataset
from torch_geometric.loader import DataLoader
from torch_geometric.nn import GNNExplainer
from torch_geometric.nn import GraphConv
from torch_geometric.nn import global_mean_pool


# Build the model
class GNN(torch.nn.Module):
    def __init__(self, hidden_channels):
        super(GNN, self).__init__()
        torch.manual_seed(12345)
        self.conv1 = GraphConv(dataset.num_node_features, hidden_channels)
        self.conv2 = GraphConv(hidden_channels, hidden_channels)

        self.conv3 = GraphConv(hidden_channels, hidden_channels)
        self.linear = Linear(hidden_channels, dataset.num_classes)

    def forward(self, x, edge_index, batch):
        x = self.conv1(x, edge_index)
        x = x.relu()
        x = self.conv2(x, edge_index)
        x = x.relu()
        x = self.conv3(x, edge_index)
        x = global_mean_pool(x, batch)
        x = F.dropout(x, p=0.5, training=self.training)
        x = self.linear(x)
        return x


# Creating the function to train the model
def Train(data_loader, loss_func):
    model.train()
    # Iterate in batches over the training dataset
    for data in data_loader:
        # Perform a single forward pass
        out = model(data.x, data.edge_index, data.batch)
        # Compute the loss
        loss = loss_func(out, data.y)
        # Derive gradients
        loss.backward()
        # Update parameters based on gradients
        optimizer.step()
        # Clear gradients
        optimizer.zero_grad()


# function to test the model
def Test(data_loader):
    model.eval()
    correct = 0
    # Iterate in batches over the training/test dataset
    for data in data_loader:
        out = model(data.x, data.edge_index, data.batch)
        # Use the class with highest probability.
        pred = out.argmax(dim=1)
        # Check against ground-truth labels.
        correct += int((pred == data.y).sum())
    # Derive ratio of correct predictions.
    return correct / len(test_loader.dataset)


if __name__ == '__main__':
    # Load the dataset
    dataset = TUDataset(root='../TUDataset', name='MUTAG')
    # print details about the graph
    print(f'Dataset: {dataset}:')
    print("Number of Graphs: ", len(dataset))
    print("Number of Freatures: ", dataset.num_features)
    print("Number of Classes: ", dataset.num_classes)

    data = dataset[0]
    print(data)
    print("No. of nodes: ", data.num_nodes)
    print("No. of Edges: ", data.num_edges)
    print(f'Average node degree: {data.num_edges / data.num_nodes:.2f}')
    print(f'Has isolated nodes: {data.has_isolated_nodes()}')
    print(f'Has self-loops: {data.has_self_loops()}')
    print(f'Is undirected: {data.is_undirected()}')

    # Create train and test dataset
    torch.manual_seed(12345)
    dataset = dataset.shuffle()

    train_dataset = dataset[:50]
    test_dataset = dataset[50:]
    print(f'Number of training graphs: {len(train_dataset)}')
    print(f'Number of test graphs:{len(test_dataset)}')

    '''graphs in graph classification datasets are usually small,
    a good idea is to batch the graphs before inputting
    them into a Graph Neural Network to guarantee full GPU utilization__
    _In pytorch Geometric adjacency matrices are stacked in a diagonal fashion
    (creating a giant graph that holds multiple isolated subgraphs), a
    nd node and target features are simply concatenated in the node dimension:
    '''
    train_loader = DataLoader(train_dataset, batch_size=64, shuffle=True)
    test_loader = DataLoader(test_dataset, batch_size=64, shuffle=False)

    for step, data in enumerate(train_loader):
        print(f'Step {step + 1}')
        print('==============')
        print(f'Number of graphs in the current batch: {data.num_graphs}')
        print(data)
        print()

    # Build the model
    model = GNN(hidden_channels=64)
    print(model)

    # set the optimizer
    optimizer = torch.optim.Adam(model.parameters(), lr=0.02)

    # set the loss function
    criterion = torch.nn.CrossEntropyLoss()

    # Train the model for 150 epochs
    for epoch in range(1, 100):
        Train(train_loader, loss_func=criterion)
        train_acc = Test(train_loader)
        test_acc = Test(test_loader)
        if epoch % 10 == 0:
            '''print(f'Epoch {epoch:>3} | Train Loss: {total_loss/len(train_loader):.3f} '
                  f'| Train Acc: {acc/len(train_loader)*100:>6.2f}% | Val Loss: '
                  f'{val_loss/len(train_loader):.2f} | Val Acc: '
                  f'{val_acc/len(train_loader)*100:.2f}%')
            '''
            print(f'Epoch: {epoch:03d}, Train Acc: {train_acc:.4f}, Test Acc: {test_acc:.4f}')

    # Explain the graph
    explainer = GNNExplainer(model, epochs=100, return_type='log_prob')
    data = dataset[0]
    node_feat_mask, edge_mask = explainer.explain_graph(data.x, data.edge_index)
    ax, G = explainer.visualize_subgraph(-1, data.edge_index, edge_mask, data.y)
    plt.show()

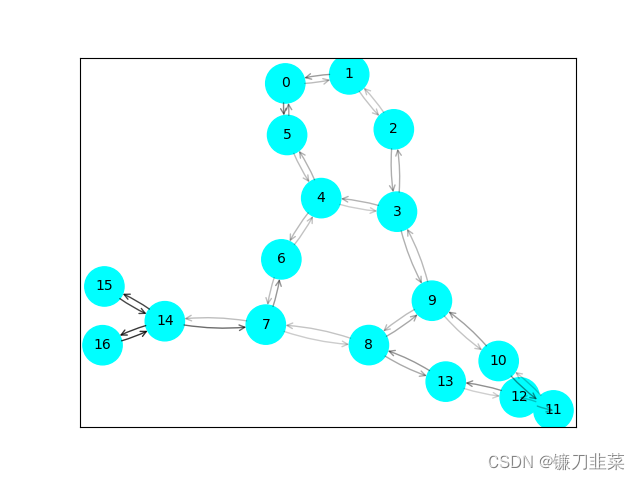
当可视化visualize_subgraph时，需要将node_idx设置为-1，因为这意味着一个图分类任务；否则会报错。

参考资料

1. 图神经网络的可解释性方法介绍和GNNExplainer解释预测的代码示例（附代码）
2. NIPS19开源论文: 万能的GNN解释器
3. GNNExplainer 个人总结
4. GNNExplainer: Generating Explanations for Graph Neural Networks
5. GNNExplainer的内部实现
6. 图解释性综述 Explainability in Graph Neural Networks
7. Explainability in Graph Neural Networks: A Taxonomic Survey