您现在的位置是：首页 >技术交流 >二叉树的非递归遍历网站首页技术交流

二叉树的非递归遍历

派小星233 2023-06-14 20:00:02
简介二叉树的非递归遍历

目录

前言：

一：前序遍历

二：中序遍历

三：后序遍历

四：层序遍历

前言：

二叉树的非递归遍历需要借助栈和队列以及二叉树的一些基础接口，这些在之前的文章中有讲过，这里就不赘述，不清楚的家人们可以点链接，这里直接给出所有需要的接口。

栈和队列：https://blog.csdn.net/2301_76269963/article/details/129823215?spm=1001.2014.3001.5501

二叉树基础接口：https://blog.csdn.net/2301_76269963/article/details/130231257?spm=1001.2014.3001.5501

代码：

//队列
struct BinaryTreeNode;
//重定义，方便更改存储类型
typedef struct BinaryTreeNode* QDataType;
//结点的结构体
typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType data;
}QNode;
//队列的结构体（头用来开辟链接，尾用来查找）
typedef struct Queue
{
	//头
	QNode* head;
	//尾
	QNode* tail;
}Queue;

//初始化
void QueueInit(Queue* pq)
{
	//断言，不能传空的结构体指针
	assert(pq);
	//初始化，把头和尾都指向空
	pq->head = pq->tail = NULL;
}

//入队列
void QueuePush(Queue* pq,QDataType x)
{
	//断言，不能传空的结构体指针
	assert(pq);
	//申请新结点
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		printf("malloc error
");
		exit(-1);
	}
	newnode->data = x;
	newnode->next = NULL;
	//如果队列为空，单独处理
	if (pq->head == NULL)
	{
		pq->head = pq->tail = newnode;
	}
	else
	{
		//原尾指向新结点（链接）
		pq->tail->next = newnode;
		//更新尾
		pq->tail = newnode;
	}
}

//队列销毁
void QueueDestroy(Queue* pq)
{
	//断言，不能传空的结构体指针
	assert(pq);
	//先保存下一个，再释放
	QNode* cur = pq->head;
	while (cur)
	{
		//记录
		QNode* next = cur->next;
		//释放
		free(cur);
		//迭代
		cur = next;
	}
	//头尾都置空
	pq->head = pq->tail = NULL;
}


//出队列（删除）
void QueuePop(Queue* pq)
{
	//断言，不能传空的结构体指针
	assert(pq);
	//断言，队列为空不能删除
	assert(!QueueEmpty(pq));
	//保存原头的下一个结点位置
	QNode* newhead = pq->head->next;
	//释放
	free(pq->head);
	//迭代
	pq->head = newhead;
	//如果删除结束了，要把tail指向空（避免野指针）
	if (pq->head == NULL)
		pq->tail = NULL;
}

//判断队列是否为空
bool QueueEmpty(Queue* pq)
{
	//断言，不能传空的结构体指针
	assert(pq);
	/*if (pq->head == NULL)
		return true;
	else
		return false;*/
	//依据判断语句的指直接返回
	return pq->head == NULL;
}

//查找队列的头数据
QDataType QueueFront(Queue* pq)
{
	//断言，不能传空的结构体指针
	assert(pq);
	//断言，队列为空不能查找
	assert(!QueueEmpty(pq));
	return pq->head->data;
}



//栈
struct BinaryTreeNode;
//重定义数据类型，方便更改
typedef struct BinaryTreeNode* STDataType;

typedef struct stack {
	//存储数据
	STDataType* a;
	//栈顶（位置）
	int top;
	//容量
	int capacity;
}ST;
//初始化
void StackInit(ST* ps)
{
	//断言，不能传空指针进来
	assert(ps );
	//一开始指向NULL
	ps->a = NULL;
	//把栈顶和容量都置为空
	ps->top = ps->capacity = 0;
}

//销毁
void StackDestroy(ST* ps)
{
	//断言，不能传空指针进来
	assert(ps );
	//栈顶和容量置为空
	ps->top = ps->capacity = 0;
	//释放空间
	free(ps->a);
	ps->a = NULL;
}

//入栈
void StackPush(ST* ps, STDataType x)
{
	//断言，不能传空指针进来
	assert(ps);
	//先判断是否扩容
	if (ps->top == ps->capacity)
	{
		int newcapacity = ps->capacity == 0 ? 4 : (ps->capacity) * 2;
		//扩容
		STDataType* tmp = 
		(STDataType*)realloc(ps->a, sizeof(STDataType) * newcapacity);
		//扩容失败
		if (tmp == NULL)
		{
			printf("realloc error
");
			exit(-1);
		}
		//更新
		ps->capacity = newcapacity;
		ps->a = tmp;
	}
	//存储数据
	ps->a[ps->top] = x;
	ps->top++;
}


//出栈（删除）
void StackPop(ST* ps)
{
	//断言，不能传空指针进来
	assert(ps);
	//如果栈为空，不能出栈
	assert(!StackEmpty(ps));
	ps->top--;
}

//取顶部数据
STDataType StackTop(ST* ps)
{
	//断言，不能传空指针进来
	assert(ps);
	//如果栈为空，不能进行访问
	assert(!StackEmpty(ps));
	//返回栈顶数据
	return ps->a[ps->top-1];
}
//判断栈是否为空
bool StackEmpty(ST* ps)
{
	//断言，不能传空指针进来
	assert(ps);
	//依据top来判断
	/*if (ps->top == 0)
		return true;
	return false;*/
	//更简洁的写法,一个判断语句的值要么为true,要么false
	return ps->top == 0;
}
//求树的节点数
int BinaryTreeSize(BTNode* root)
{
	/*if (root == NULL)
	{
		return 0;
	}
	return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;*/
	//更加简洁的写法
	return root == NULL ? 0 :
		BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

//手动建立一个二叉树
int main()
{
	BTNode* nodeA = BuyNewNode('A');
	BTNode* nodeB = BuyNewNode('B');
	BTNode* nodeC = BuyNewNode('C');
	nodeA->left = nodeB;
	nodeA->right = nodeC;
	BTNode* nodeD = BuyNewNode('D');
	BTNode* nodeE = BuyNewNode('E');
	BTNode* nodeF = BuyNewNode('F');
	nodeB->left = nodeD;
	nodeC->left = nodeE;
	nodeC->right = nodeF;
}

一：前序遍历

思路(配合代码和后面的图解看)：

  1. 将根节点入栈，设计一个指针p遍历节点
  2. 只要栈不为空或者p不为空，就进行循环
  3. 节点不为空，先打印节点数据，再入栈，让指针指向节点左孩子
  4. 节点为空，取到栈顶数据(节点父亲)，出栈，让指针指向父亲右孩子
  5. p为空并且栈为空，结束

代码：

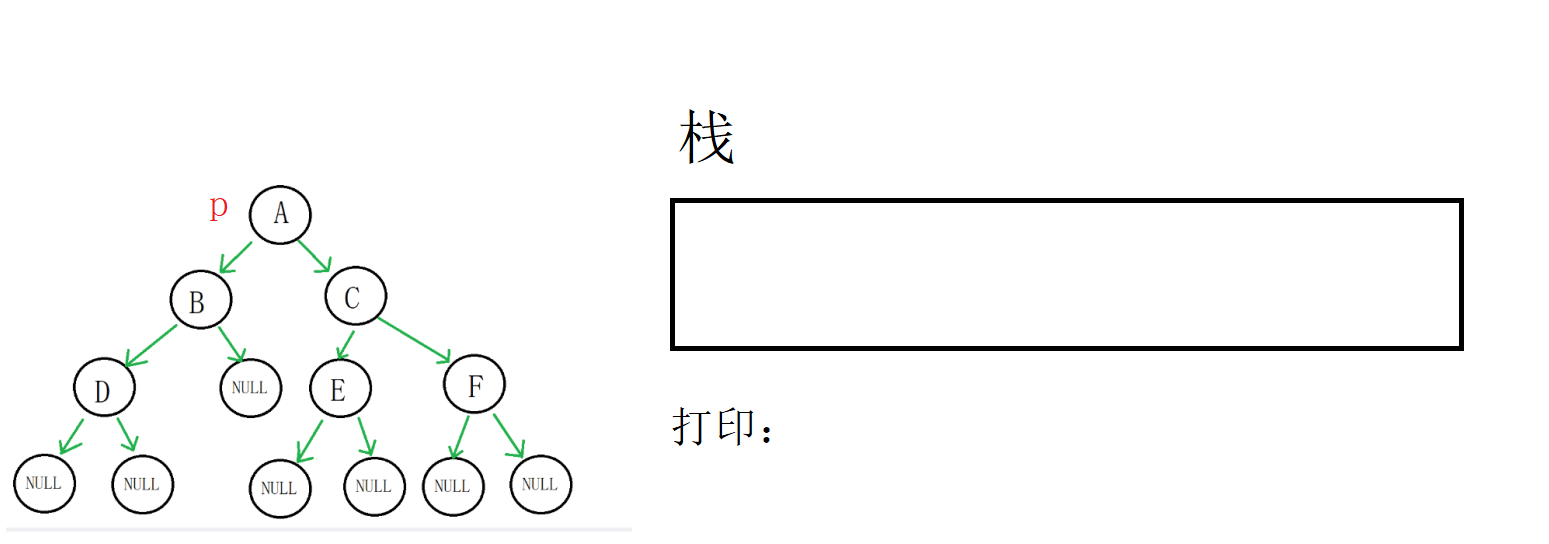
//非递归前序遍历
void NotRecPreOrder(BTNode* root)
{
	ST s;
	StackInit(&s);
	BTNode* p = root;

	while (!StackEmpty(&s) || p)
	{
		//不为空
		if (p)
		{
			//入栈
			StackPush(&s, p);
			printf("%c ", p->data);
			p = p->left;
		}
		//为空
		else
		{
			//拿到栈顶
			p = StackTop(&s);
			StackPop(&s);
			p = p->right;
		}
	}
	StackDestroy(&s);
}

图解：

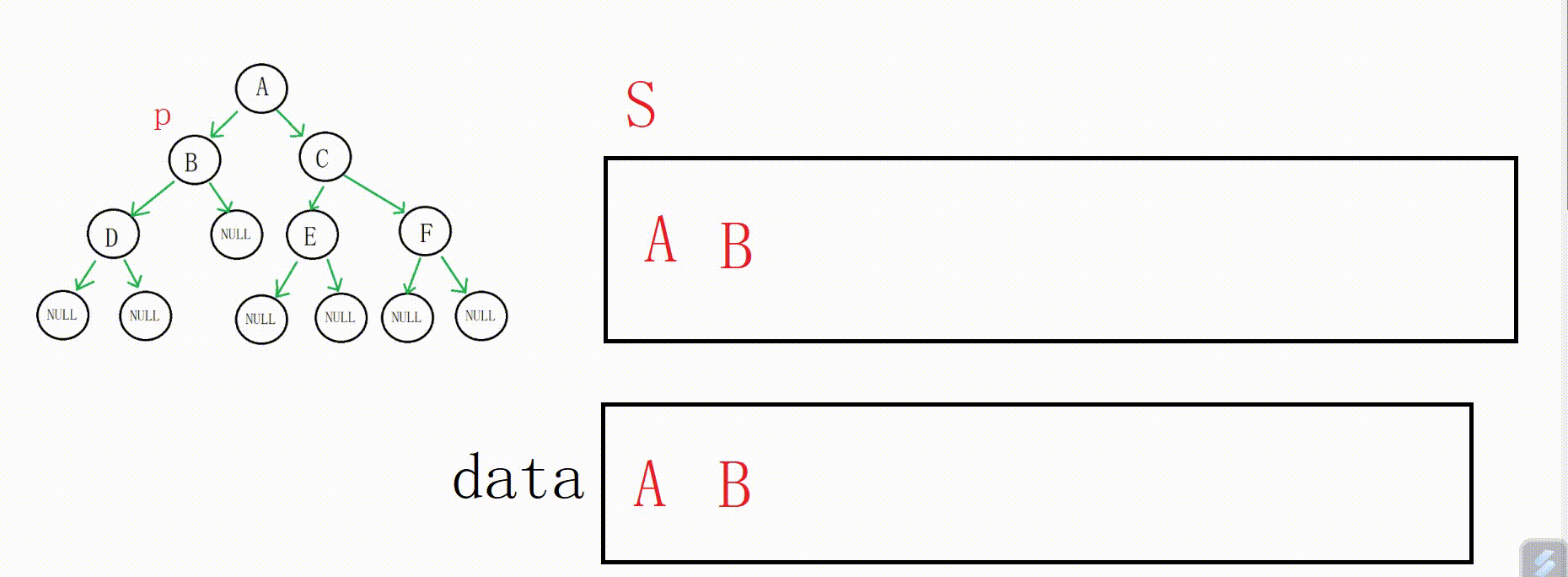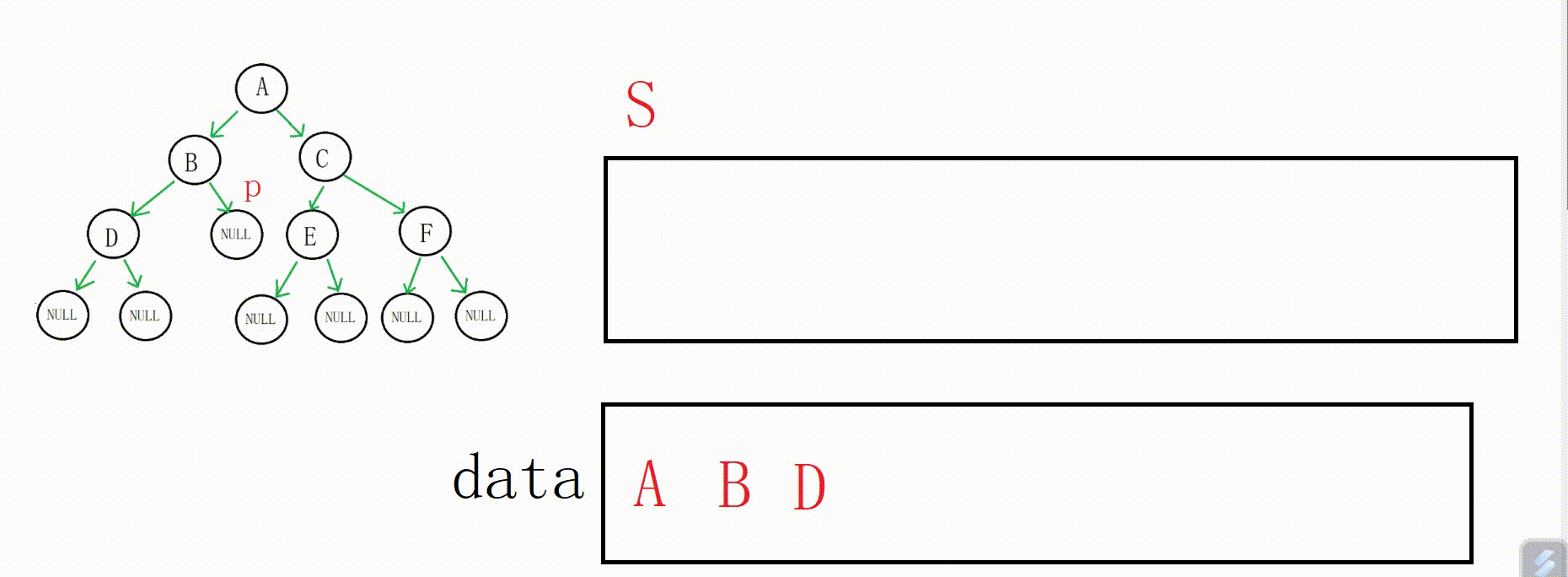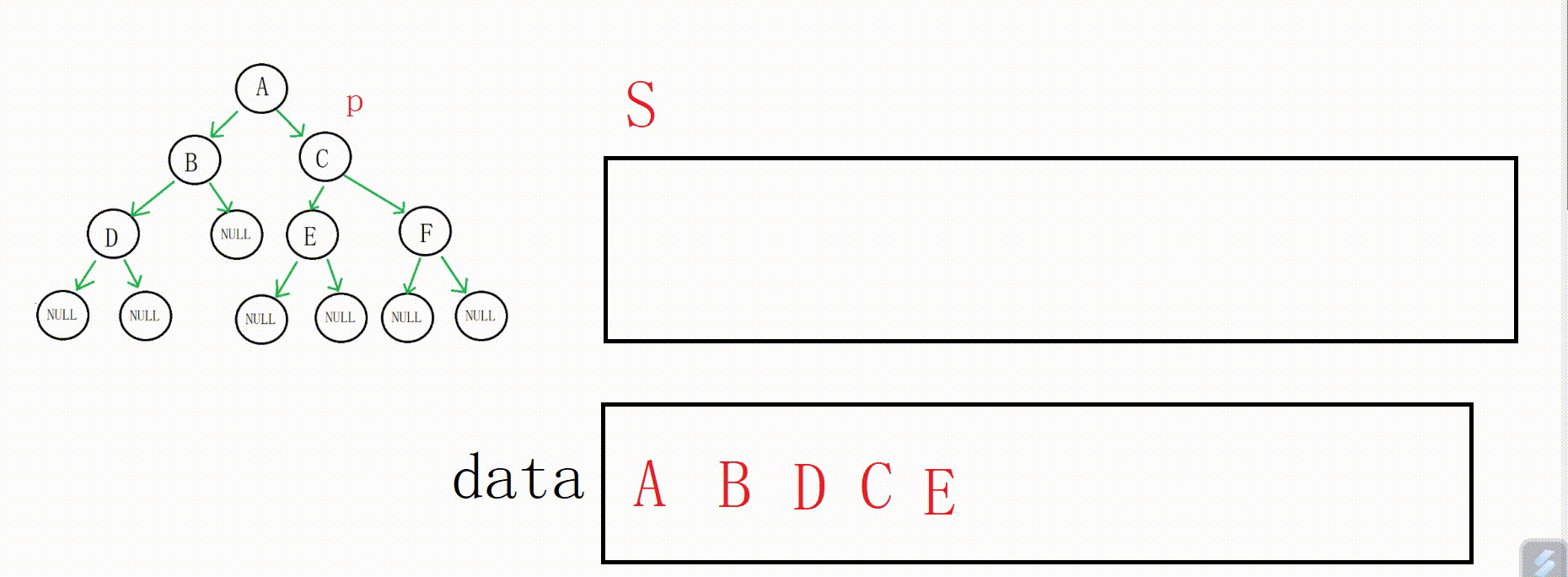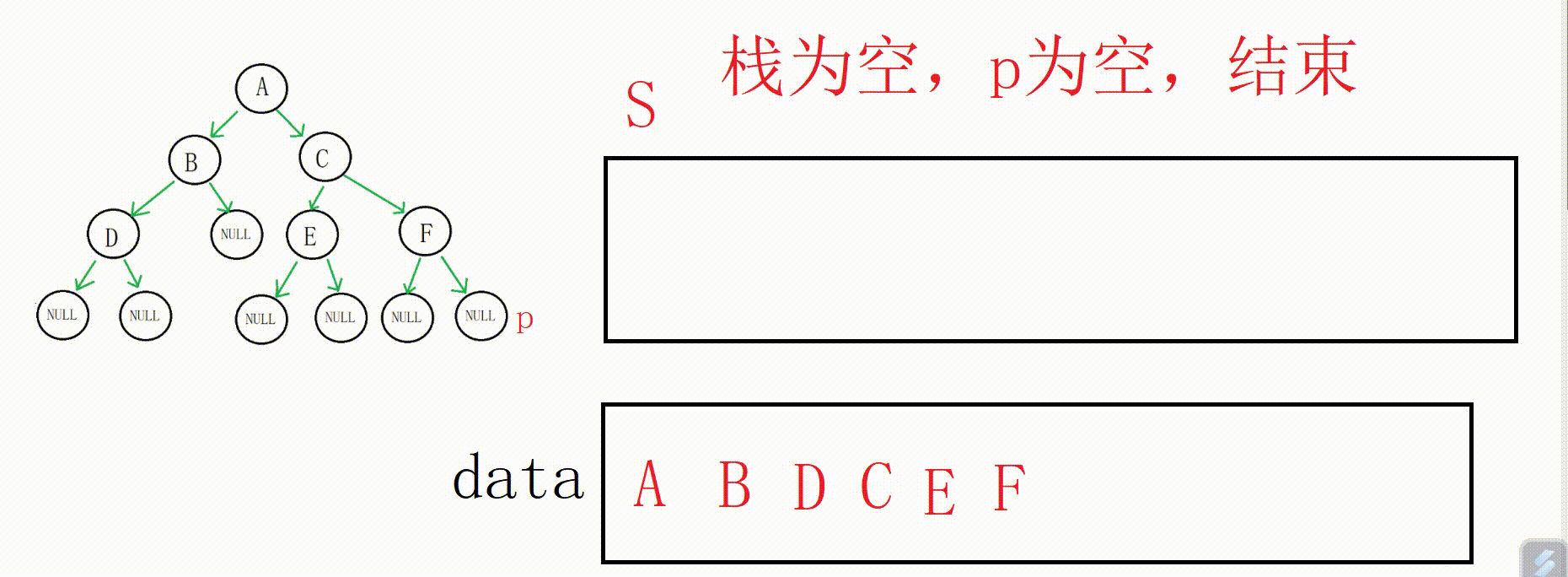
一开始p不为空，我们把A打印，入栈，p指向B

p又不为空，我们把B打印，入栈，p指向D

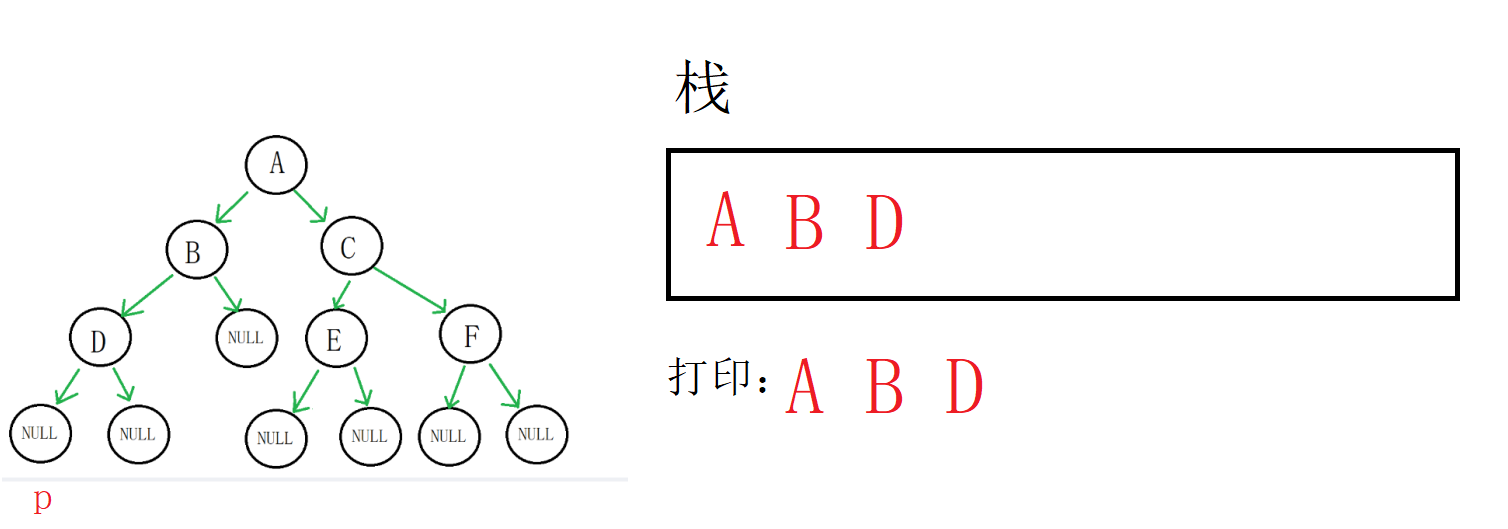
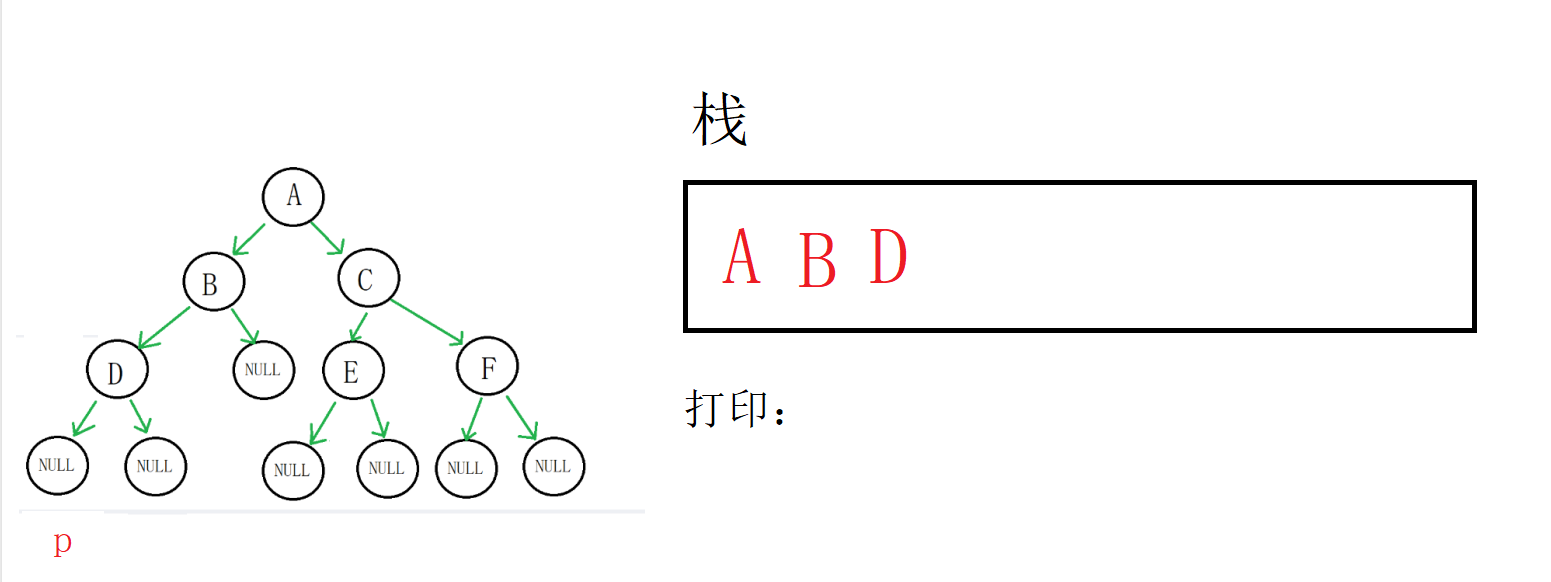
p又不为空，我们把D打印，入栈，p指向空

 

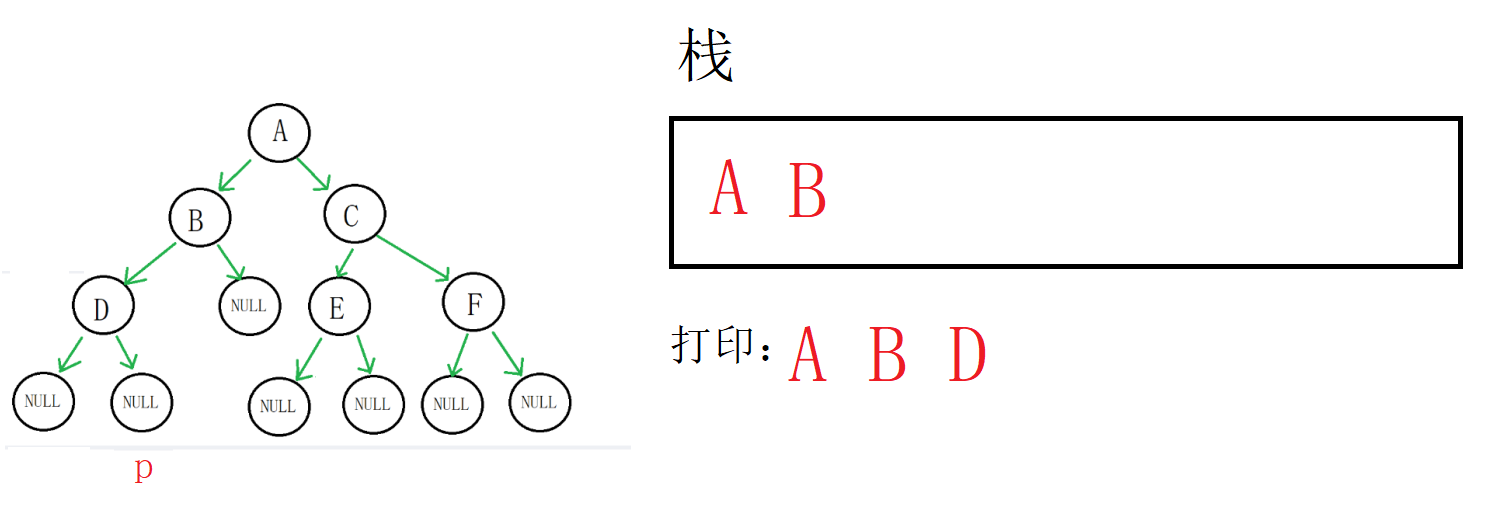
然后就是重点了，p为空， 我们拿到栈顶数据，也就是D(地址)，然后出栈，p指向D的右孩子

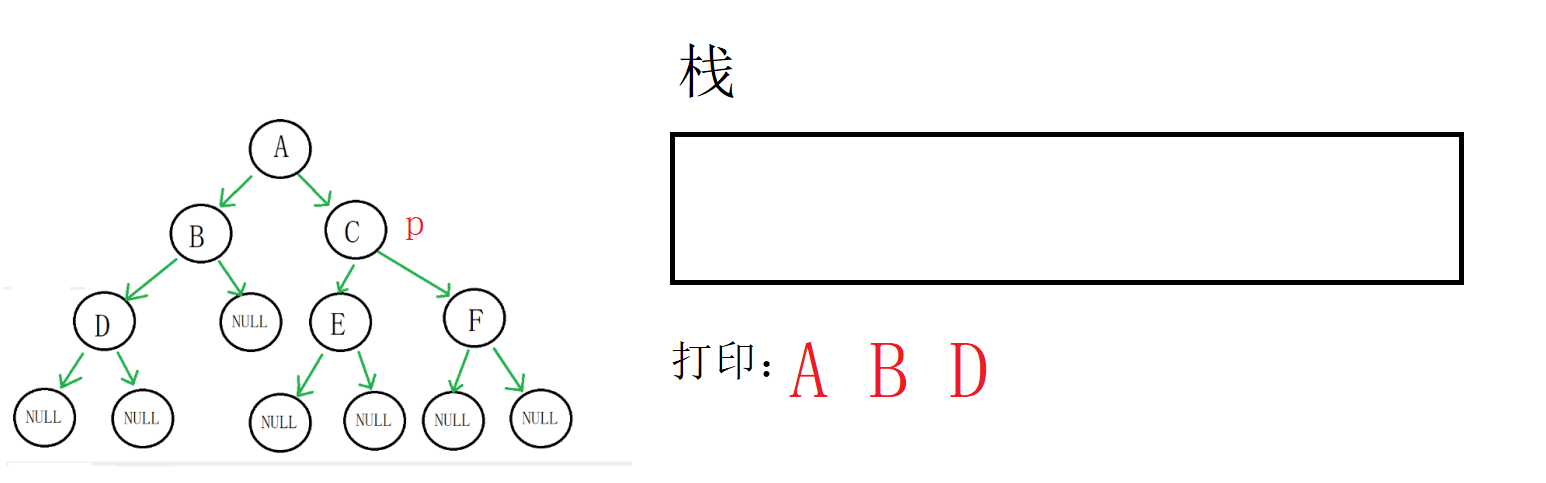
右孩子也为空，再拿到栈顶(B地址)，出栈，p指向B的右孩子，这个时候以B为根的树的左子树就遍历完了，开始遍历B的右子树

B的右子树为空，再拿到栈顶(A地址),出栈，这个时候以A为根的树的左子树就遍历完了，开始遍历右子树，重复这个过程一直到栈空p空，就可以遍历整棵树。

二：中序遍历

思路(配合代码和图解)：

  1. 将根节点入栈，设计一个指针p用来遍历节点
  2. 只要栈不为空或者p不为空，就进行循环
  3. 节点不为空，入栈，让指针指向节点左孩子
  4. 节点为空(这个时候父亲节点的左子树一定遍历完了)，取到栈顶数据(节点父亲)，出栈，打印，让指针指向父亲右孩子
  5. p为空并且栈为空，结束

代码：

//非递归中序遍历
void NotRecInOrder(BTNode* root)
{
	BTNode* p = root;
	ST s;
	StackInit(&s);

	while (p || !StackEmpty(&s))
	{
		//不为空
		if (p)
		{
			StackPush(&s, p);
			p = p->left;
		}
		//为空
		else
		{
			//拿到栈顶
			p = StackTop(&s);
			//出栈
			StackPop(&s);
			printf("%c ", p->data);
			p = p->right;
		}
	}
	StackDestroy(&s);

}

图解：

一开始p不为空，我们把A入栈，p指向B

p又不为空，我们把B入栈，p指向D

p又不为空，我们把D入栈，p指向空

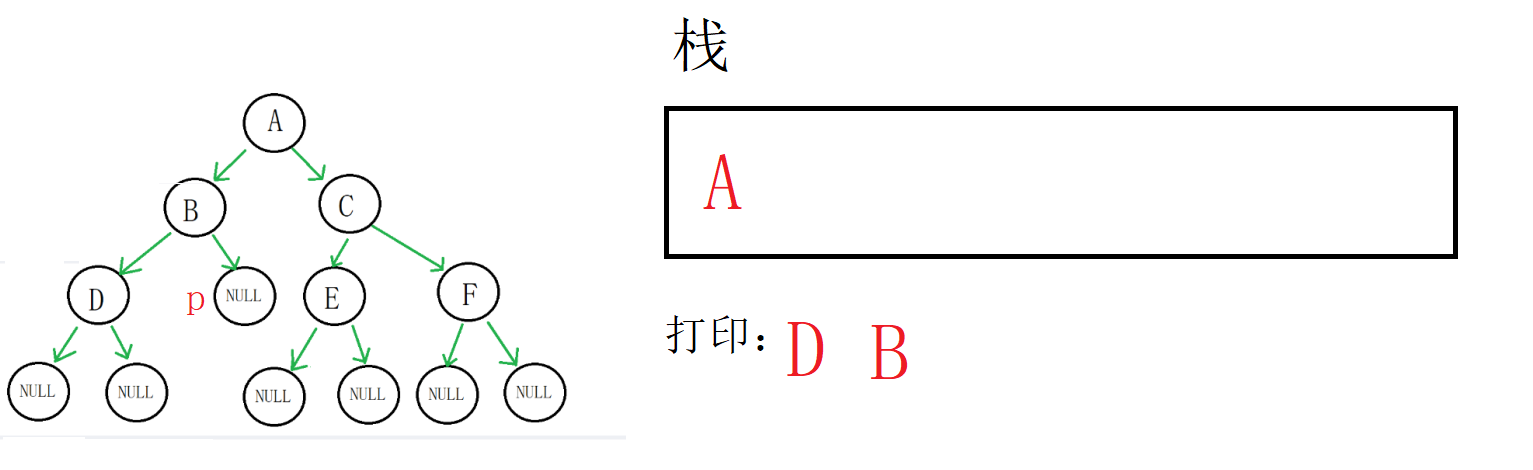
接下来就是关键点了，p为空，这个时候以D为根的树的左子树完成遍历，拿到栈顶(D地址)，出栈，然后打印数据，p指向D右孩子。

D右孩子也为空，以B为根的树的左子树完成遍历，拿到栈顶数据(B地址)，出栈，打印数据，p指向B右孩子

B的右孩子为空，再拿到栈顶(A地址),出栈，打印数据，这个时候以A为根的树的左子树就遍历完了，开始遍历右子树，重复这个过程一直到栈空p空，就可以遍历整棵树。

三：后序遍历

思路(配合代码和图解)：

  1. 将根节点入栈，设计一个指针p用来遍历节点
  2. 只要栈不为空或者p不为空，就进行循环
  3. 节点不为空，入栈，让指针指向节点左孩子
  4. 和前序中序不同，节点为空的时候我们不知道父亲的左右子树是否完成遍历，我们需要设计一个标记数组来判断栈顶节点左右子树是否完成遍历
  5. 第一次进入else内部一定是左子树完成遍历，取到栈顶数据(节点父亲)，让指针指向父亲右孩子，标记为1
  6. 如果进入else内部时标记为1，取到栈顶数据(节点父亲)，出栈，打印，循环这个过程一直到标记为0的节点，取到这个节点地址，p指向这个节点右孩子
  7. tag数组下标为0的位置是没有被使用的，如果根部节点的左右子树遍历完成，这个时候再访问根部遍历就结束了，我们把下标1的位置给根部节点，这样遍历完成后下标0的位置数据为0，可以跳出循环
  8. while循环结束后如果栈为空，代表根部节点已经访问，由于后序遍历根部是最后访问的，这个时候遍历结束，应该跳出循环

代码：

//非递归后序遍历
void NotRecPostOrder1(BTNode* root)
{
	ST s;
	StackInit(&s);
	BTNode* p = root;
	//作为遍历了左子树的依据
	//根据节点数量开辟足够空间
	char* tag = (char*)malloc(sizeof(char) * BinaryTreeSize(root));
	if (tag == NULL)
	{
		printf("malloc error
");
		exit(-1);
	}
	while (p || !StackEmpty(&s))
	{
		if (p)
		{
			StackPush(&s, p);
			tag[s.top] = '0';//标志结点是否遍历右子树
			p = p->left;
		}
		else
		{
			//如果已经遍历了左子树
			while(tag[s.top] == '1')
			{
				p = StackTop(&s);
				StackPop(&s);
				printf("%c ", p->data);
			}
			if (StackEmpty(&s))
			{
				break;
			}
			//没遍历右子树的情况取到栈顶，遍历右子树
			//遍历了右子树，取得栈顶，遍历上一层的右子树
			p = StackTop(&s);
			p = p->right;
			tag[s.top] = '1';
		}
	}
	StackDestroy(&s);
}

图解：

一开始p指向A，不为空，A(地址)入栈，p指向A左孩子，栈顶标记为0

p指向B，不为空，B入栈，p指向B的左孩子，栈顶标记为0

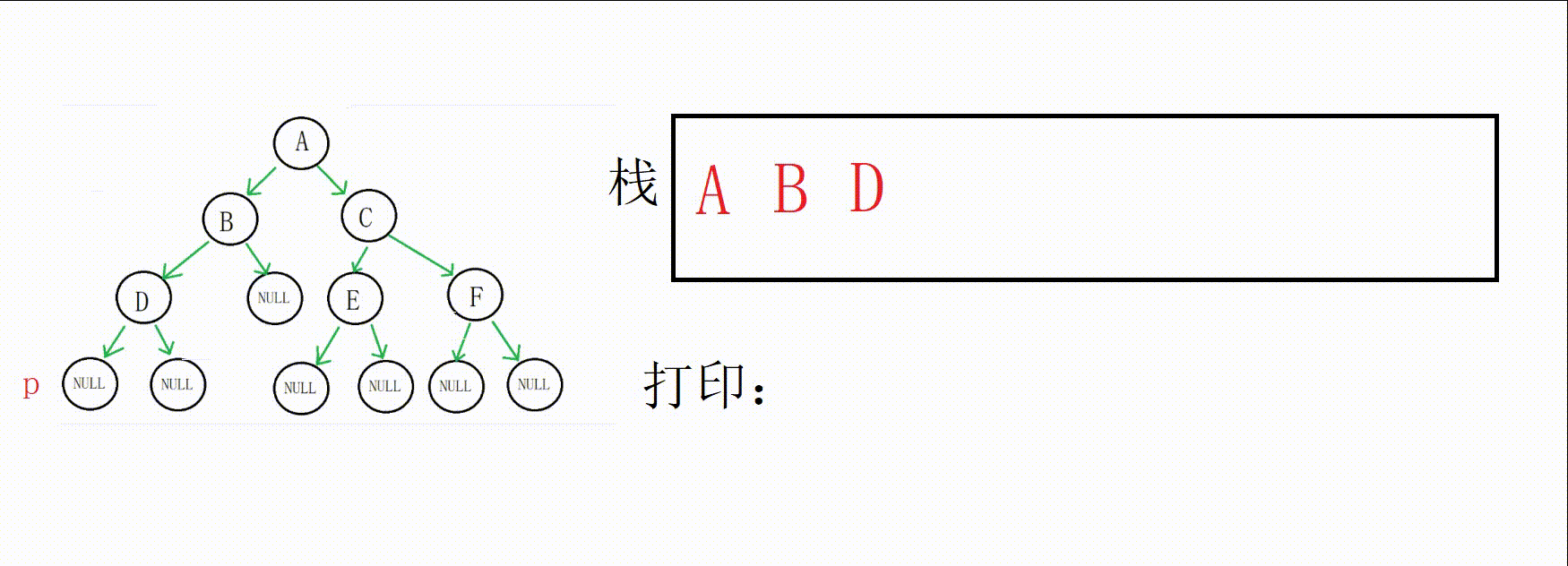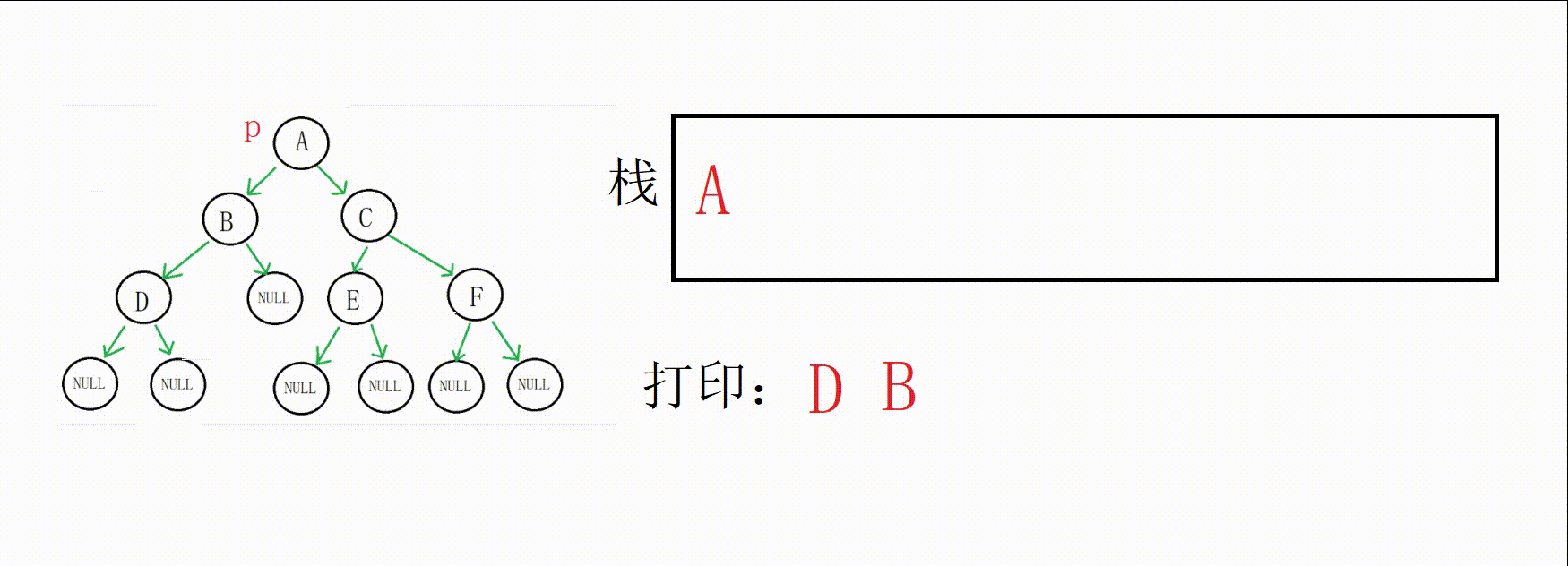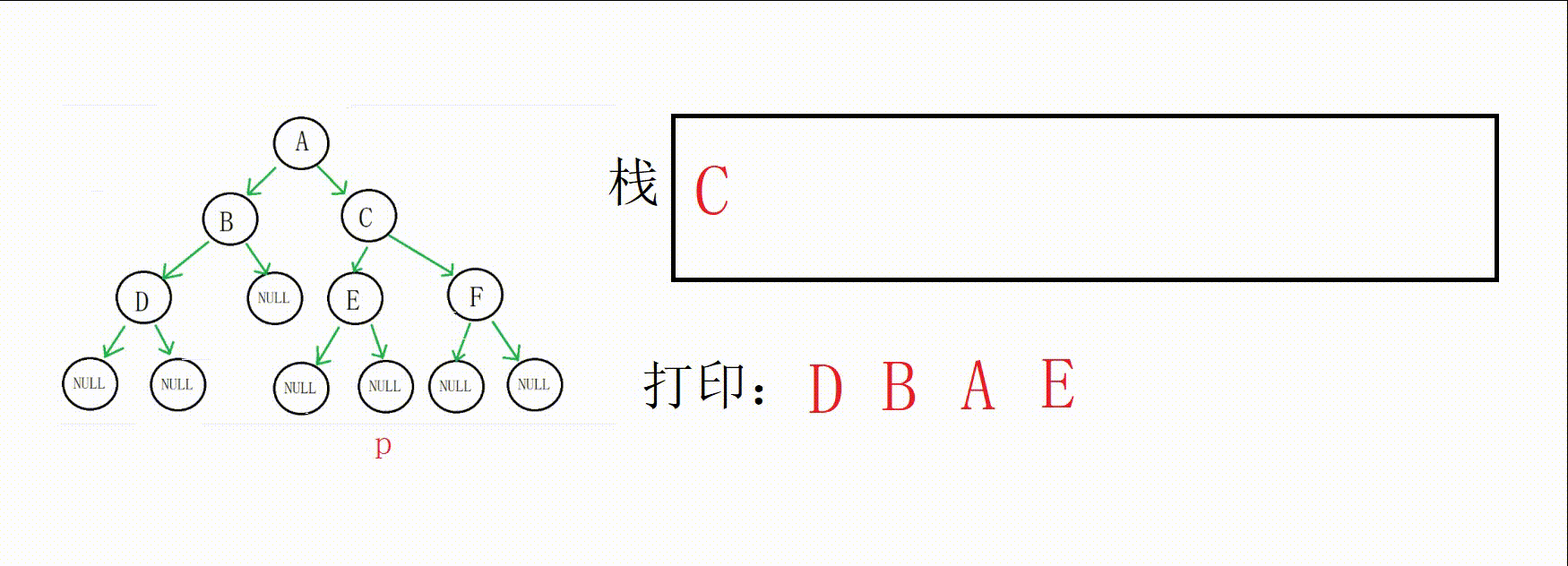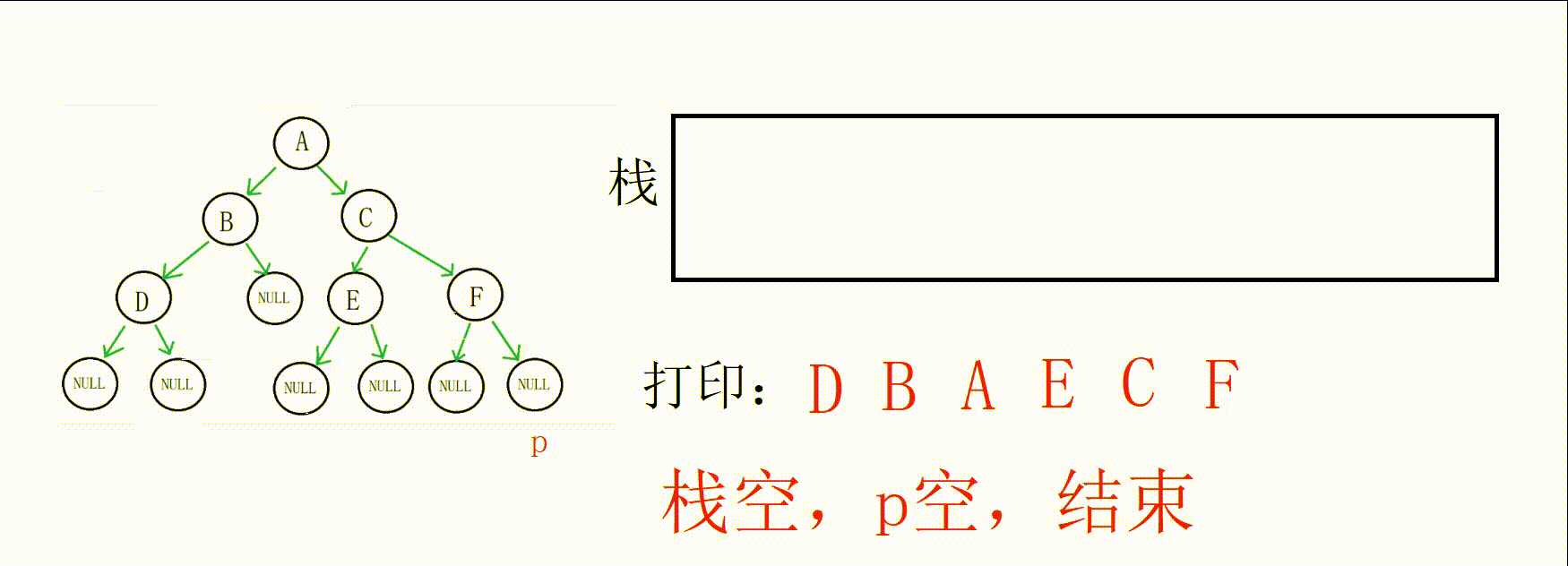
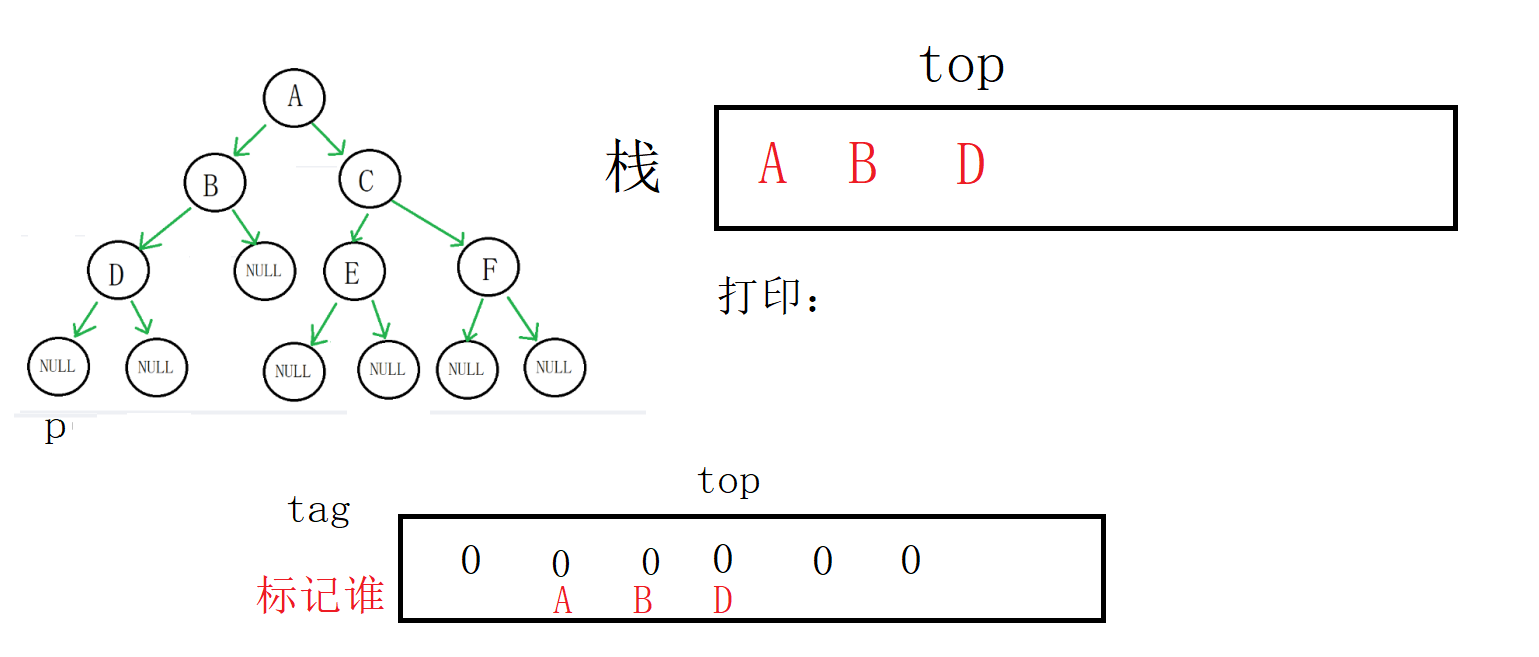
p指向D，不为空，D入栈，p指向D的左孩子，栈顶标记为0

接下来就是比较关键的地方了，p为空，进入else

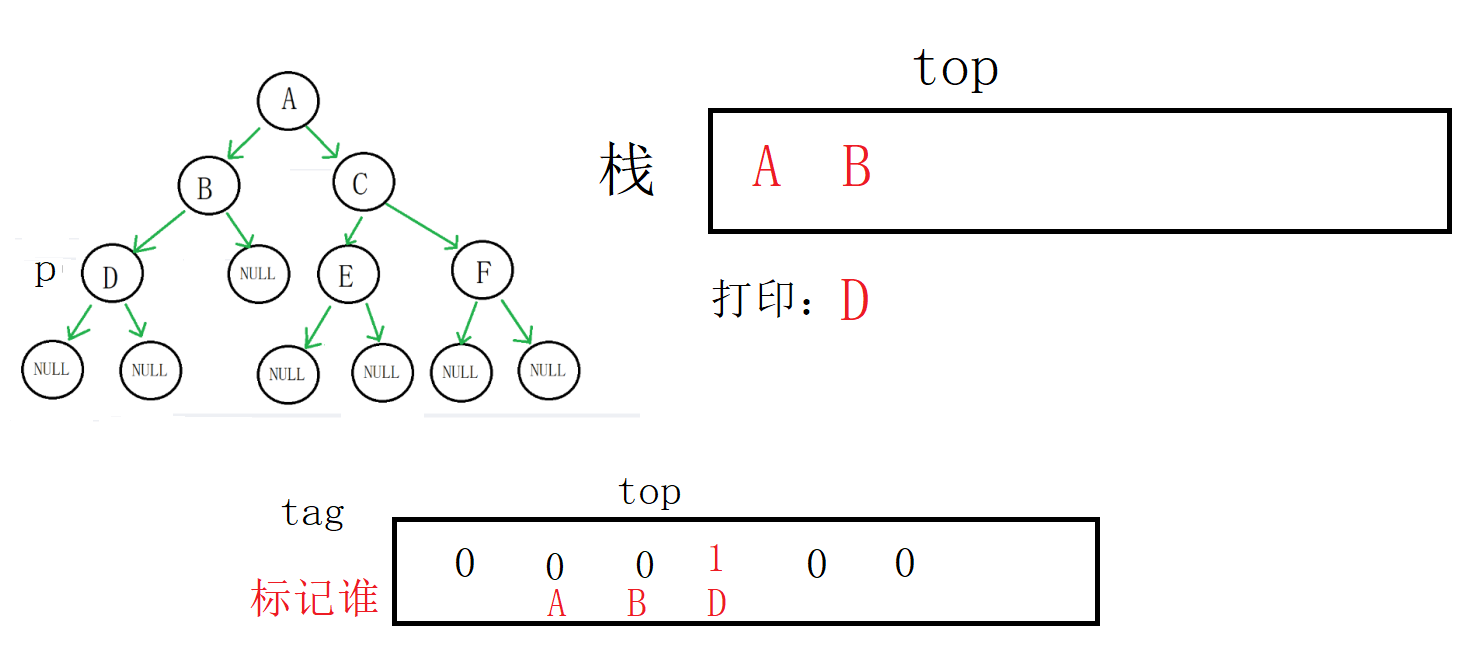
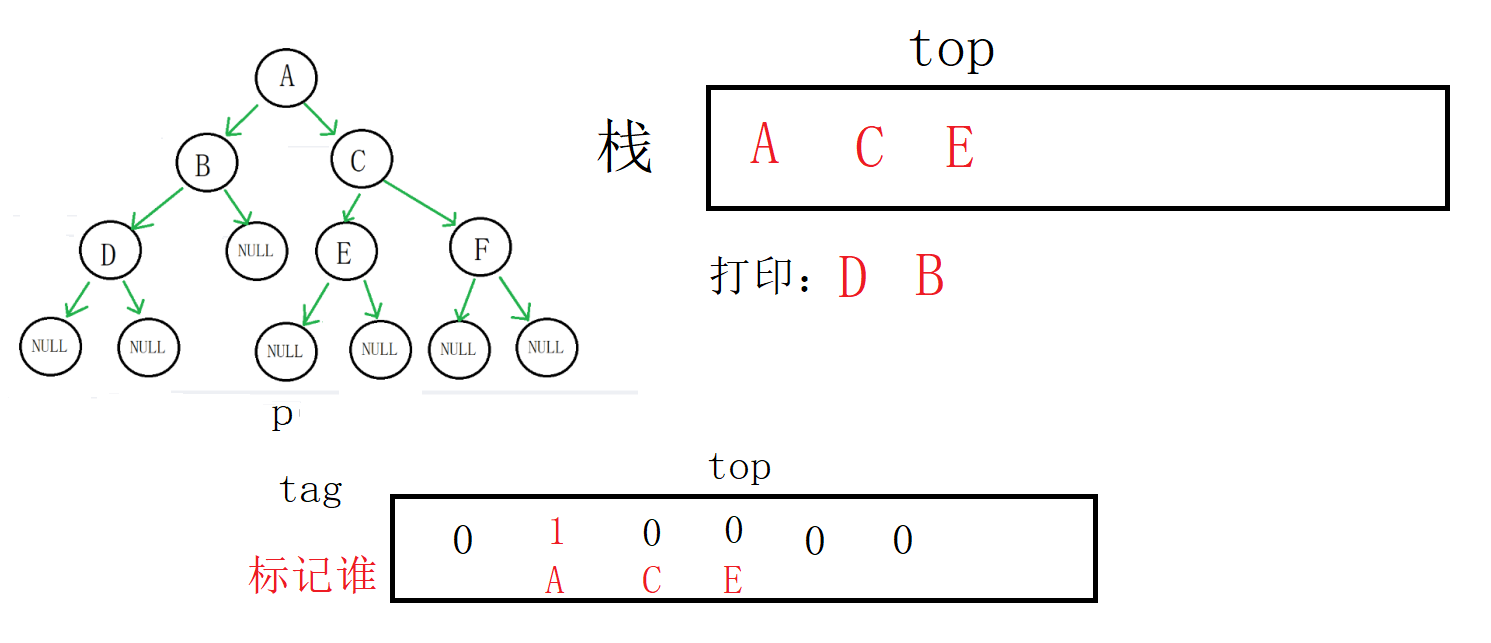
但是栈顶(D)的标记为0，代表它的左右子树还没有完成遍历

我们不进入while循环，取到栈顶数据(D地址)，然后p指向D的右孩子，将标记修改为1 

 

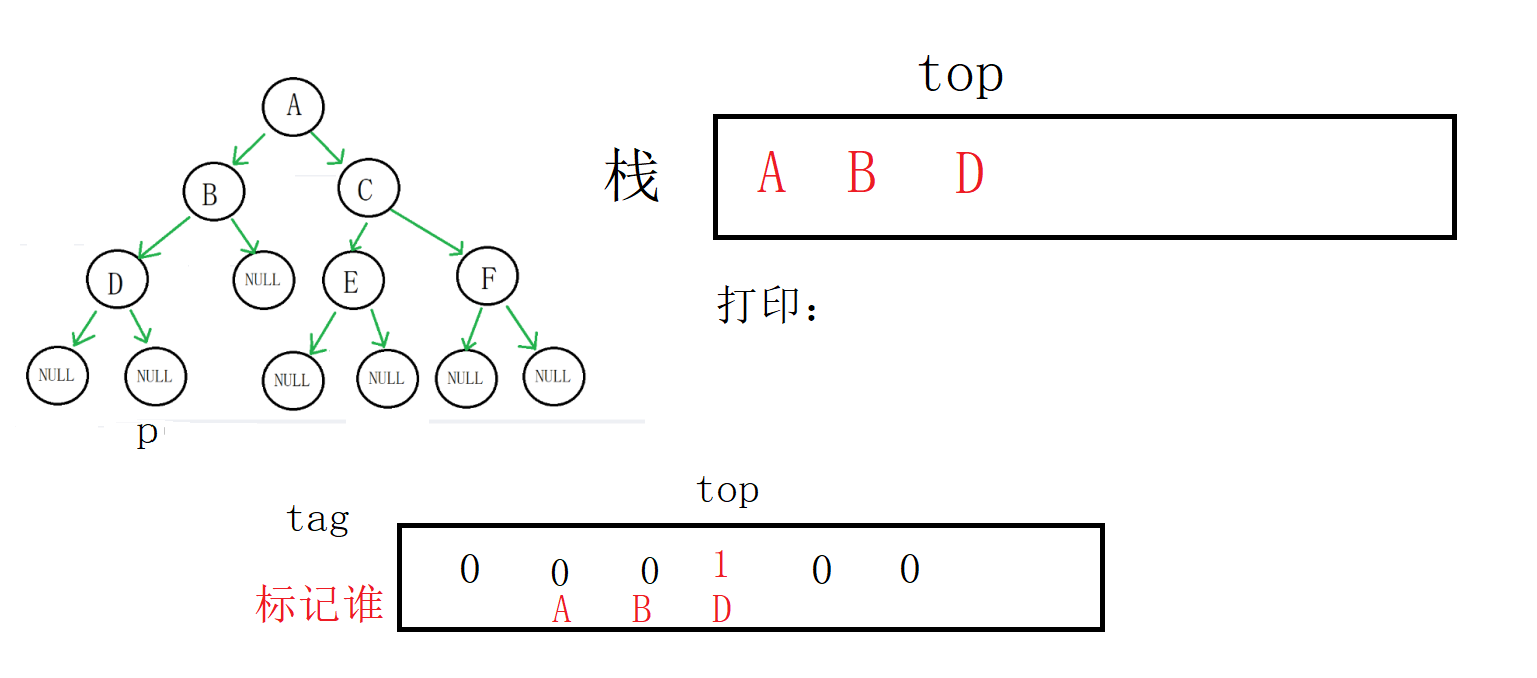
p为空，进入else

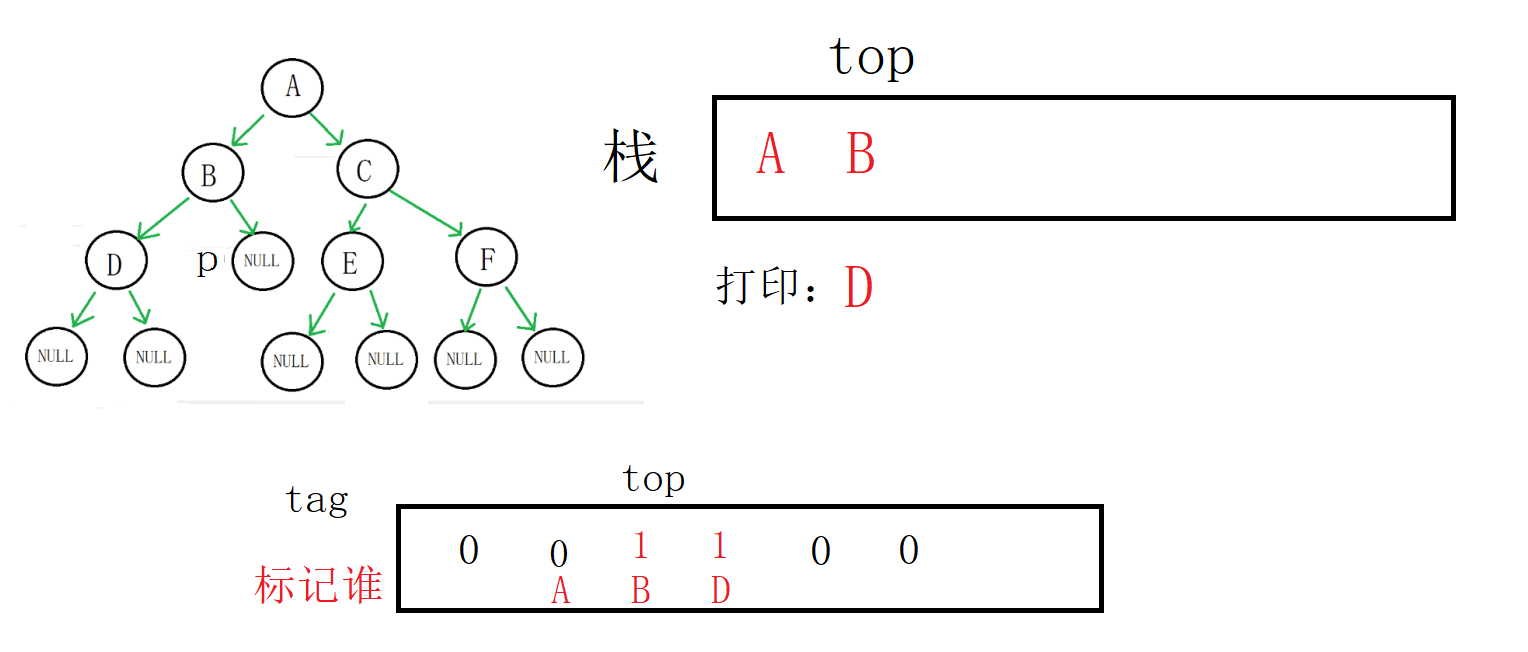
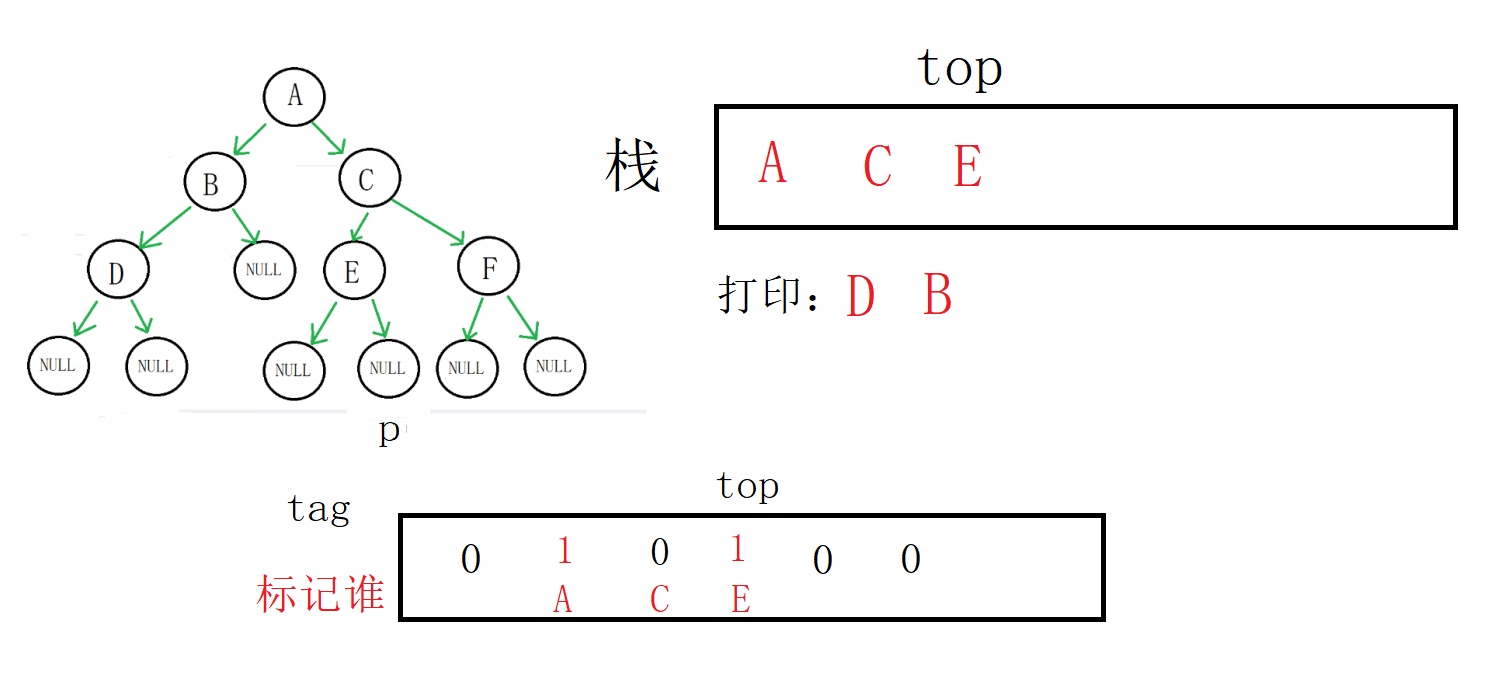
这个时候D的左右子树完成遍历，栈顶的标记为1，进入while循环

取到栈顶数据(D地址)，出栈，打印

这个时候tag[top]为0，代表B的左右子树还没有完成遍历，跳出循环

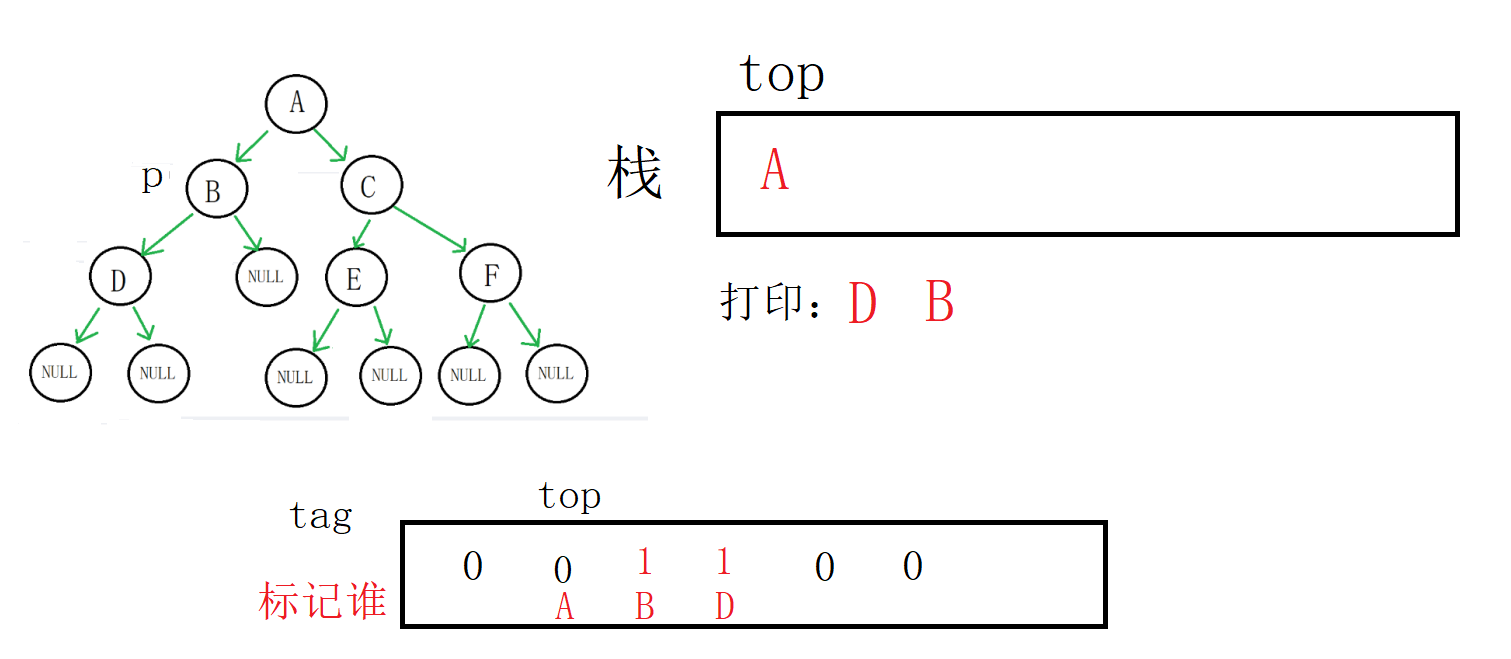
取到栈顶数据(B地址)，p指向B的右孩子，标记修改为1

p为空，进入else

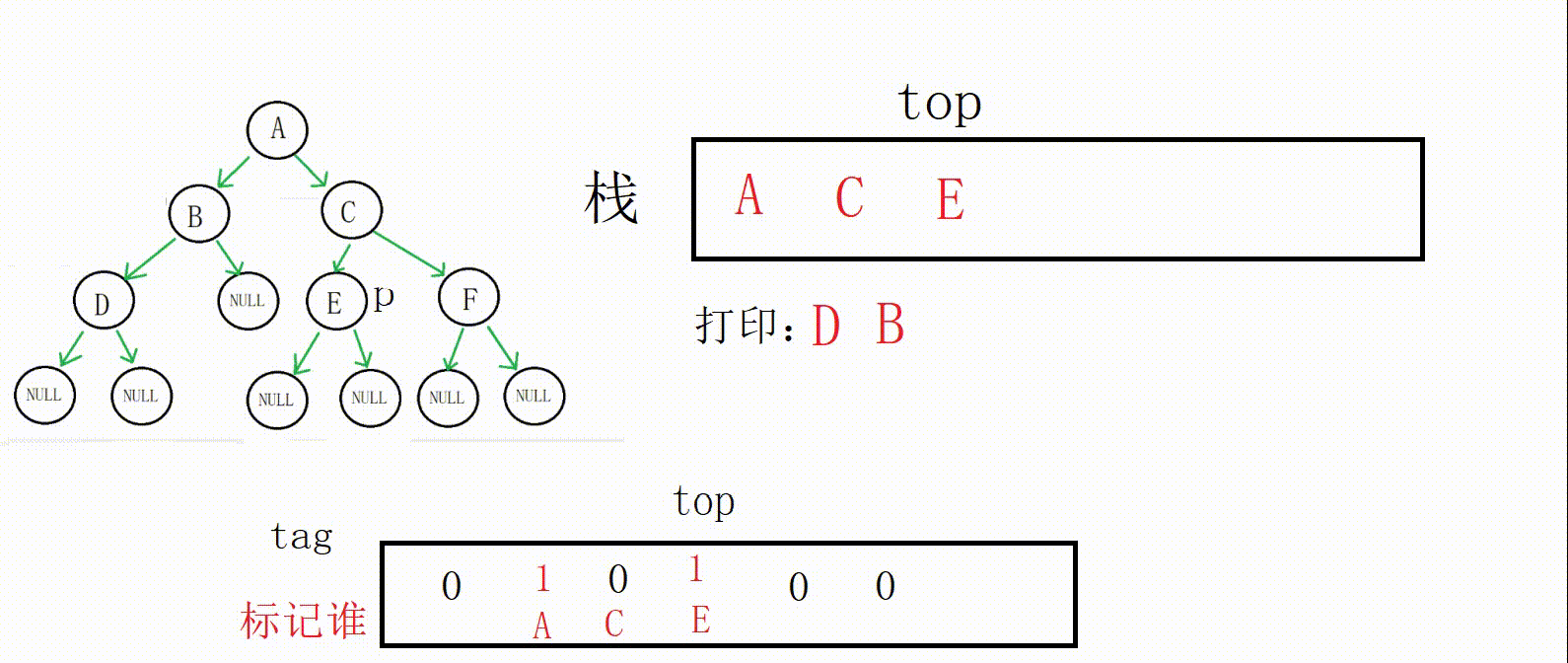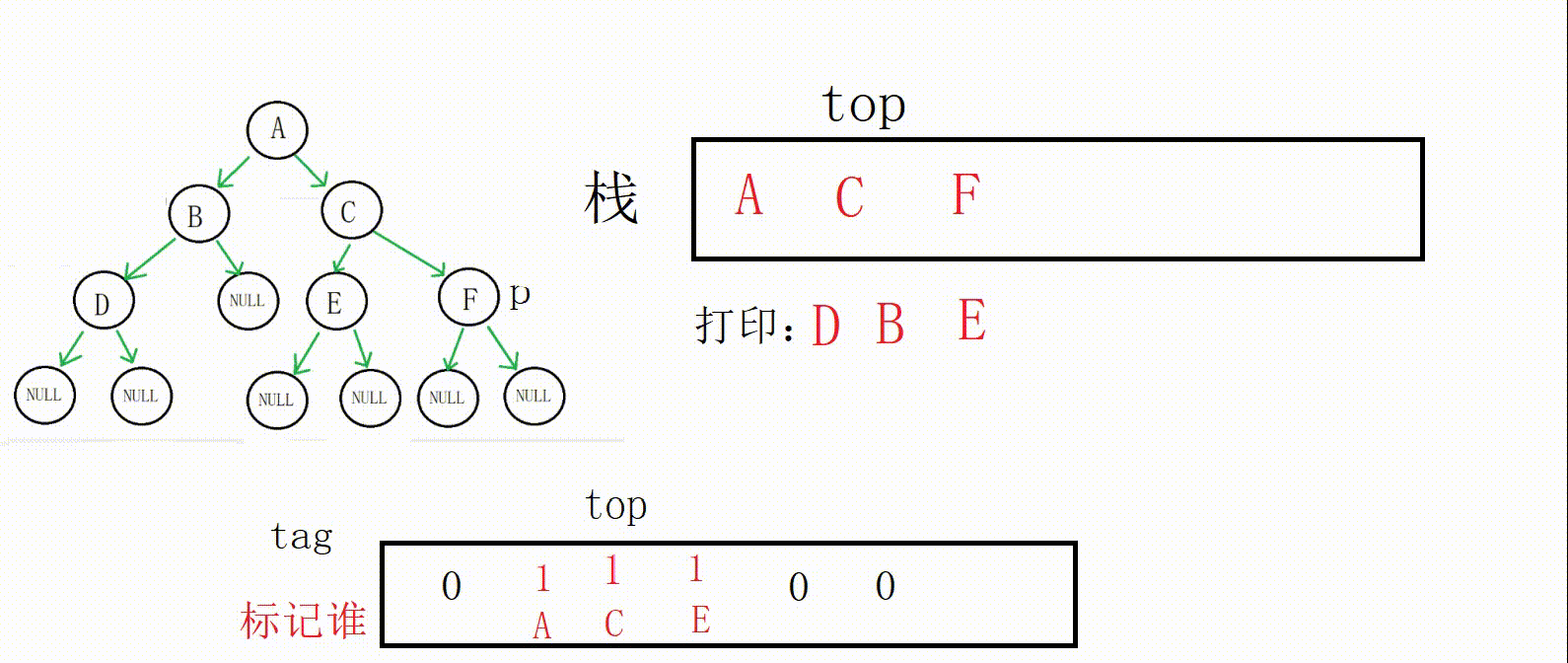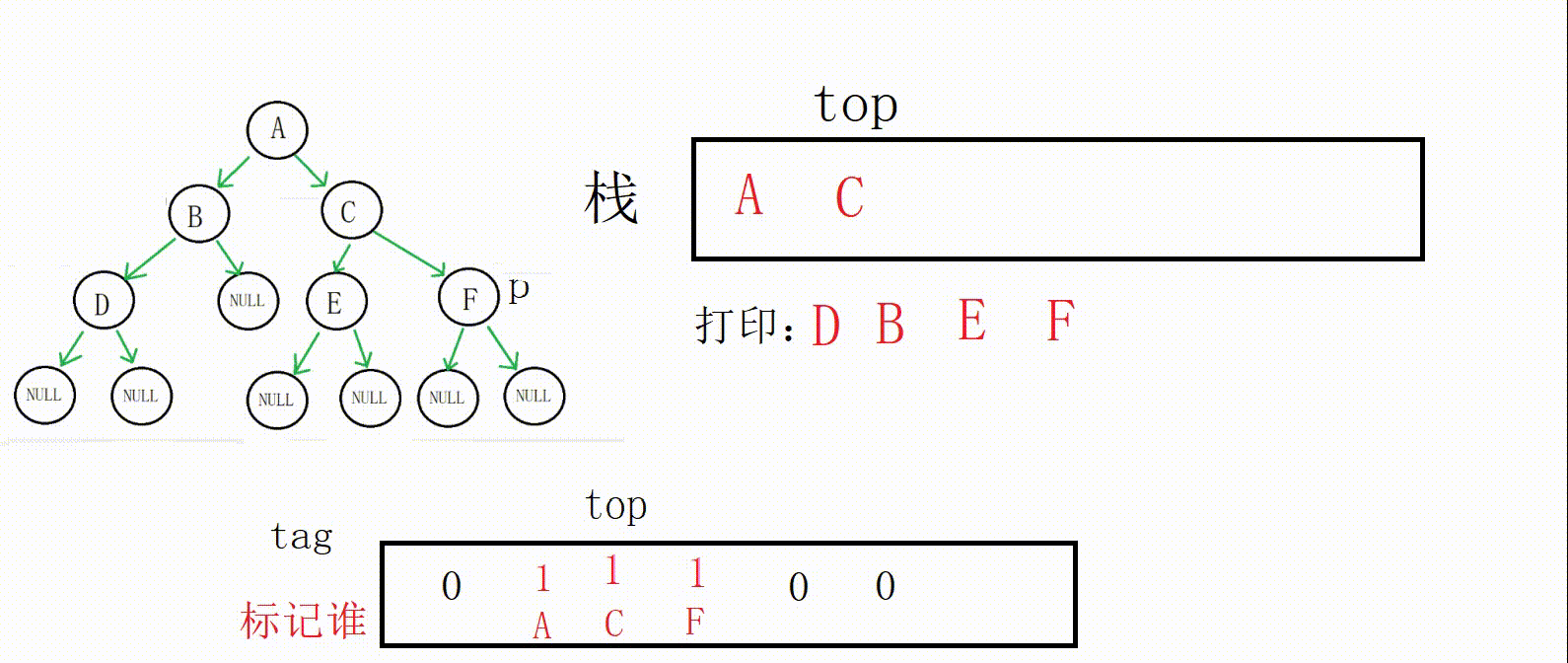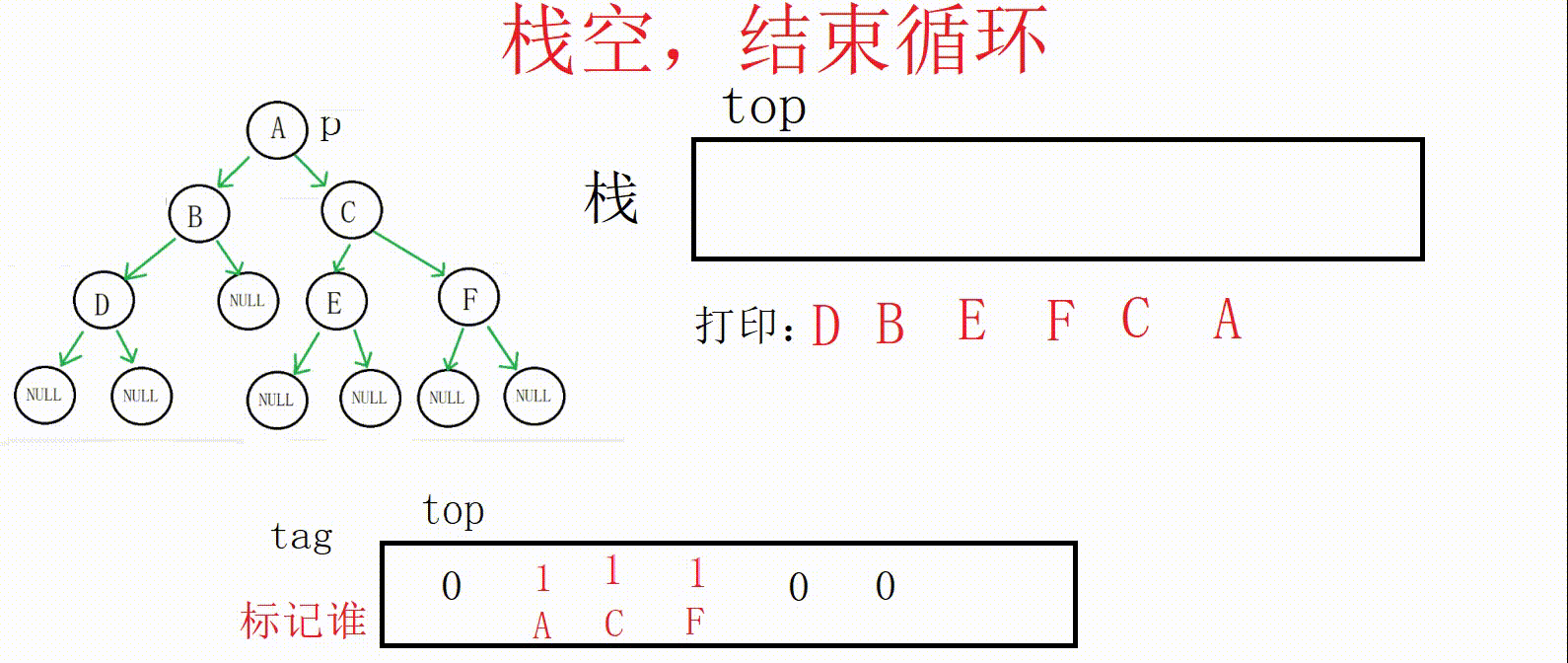
这个时候B的左右子树完成遍历，栈顶的标记为1，进入while循环

取到栈顶数据(D地址)，出栈，打印

这个时候tag[top]为0，代表A的左右子树还没有完成遍历，跳出循环

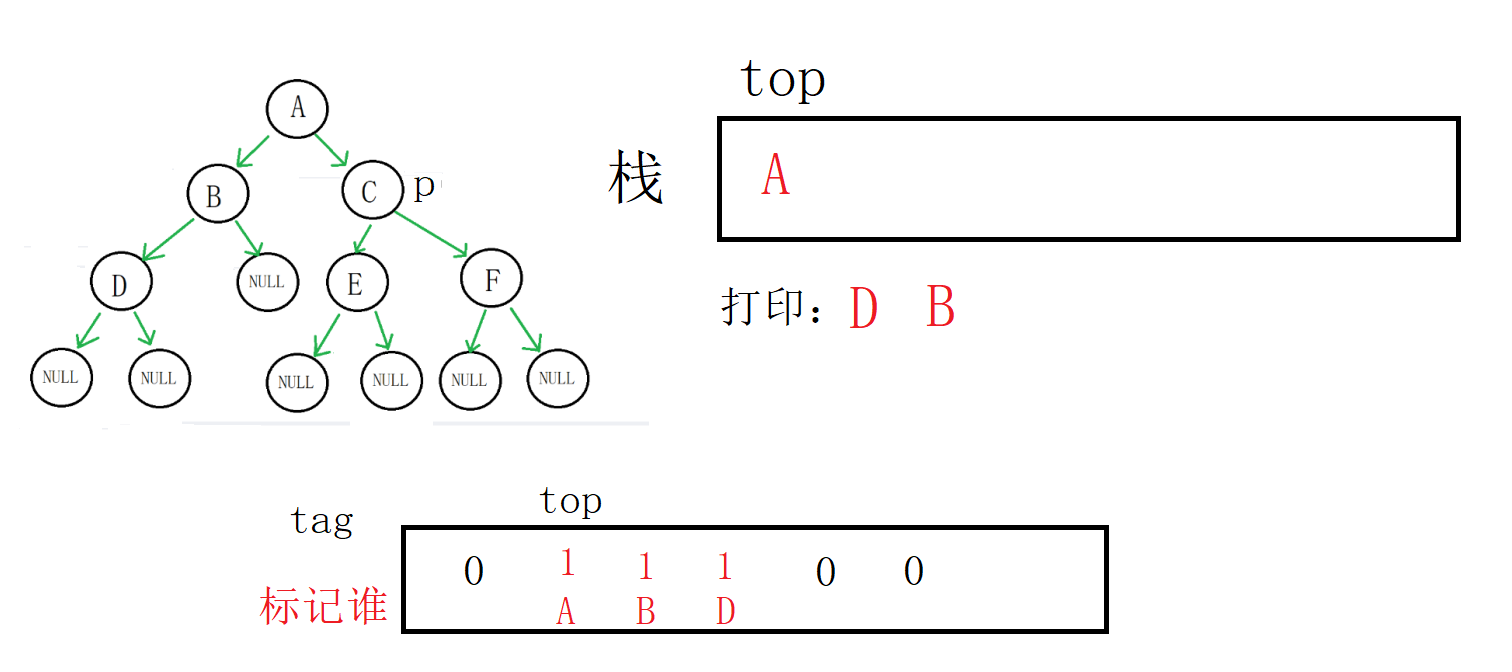
取到栈顶数据(A地址)，p指向A的右孩子，标记修改为1

p不为空，C(地址)入栈，p指向C左孩子，栈顶标记为0

p指向E，不为空，E入栈，p指向E的左孩子，栈顶标记为0

p为空，进入else

但是栈顶(E)的标记为0，代表它的左右子树还没有完成遍历

我们不进入while循环，取到栈顶数据(E地址)，然后p指向E的右孩子，将标记修改为1 

重复上述步骤

 

 跳出while循环后如果栈为空，代表整棵树已经遍历完成，结束循环

四：层序遍历

思路(配合代码和图解)：

  1. 将根节点插入队列中，设计一个指针p来遍历节点
  2. 只要队列不为空，就进行循环
  3. 循环中先取到队头数据(地址)，然后打印节点数据，最后出队列
  4. 出队列后若该节点有左节点，则将其左节点插入队列中；若该节点有右节点，则将其右节点插入队列中
  5. 队列为空，循环结束(简单来说就是父亲带出孩子)

代码：

//层序遍历
void LevelOrder(BTNode* root)
{
	assert(root);
	Queue Q;
	QueueInit(&Q);
	BTNode* p = root;
	//放入首节点
	QueuePush(&Q, p);

	while (!QueueEmpty(&Q))
	{
		p = QueueFront(&Q);
		printf("%c ", p->data);
		QueuePop(&Q);
		//左入
		if (p->left != NULL)
		{
			QueuePush(&Q, p->left);
		}
		//右入
		if (p->right != NULL)
		{
			QueuePush(&Q, p->right);
		}
	}
	//销毁队列
	QueueDestroy(&Q);
}

图解：

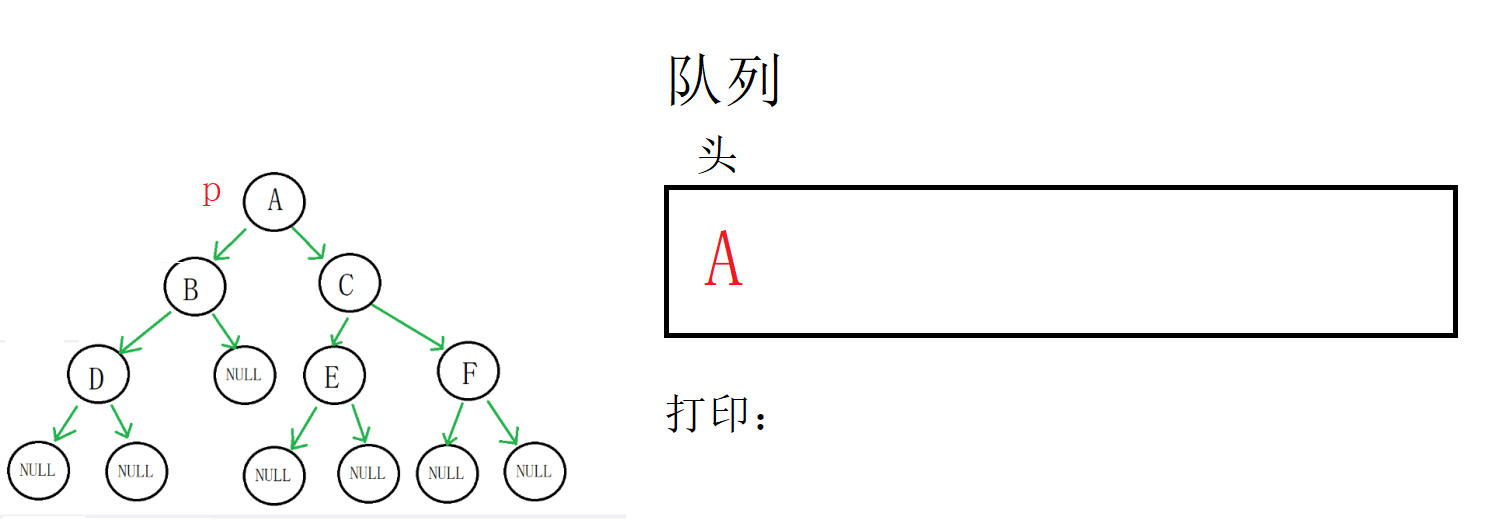
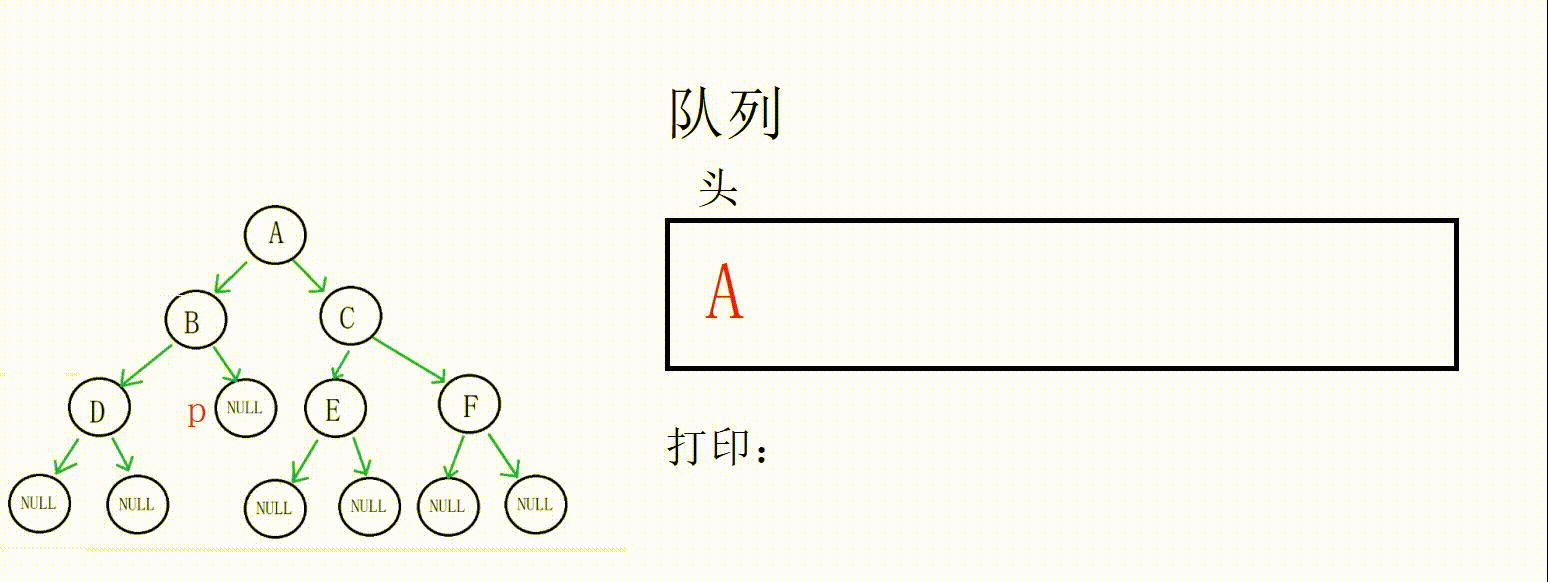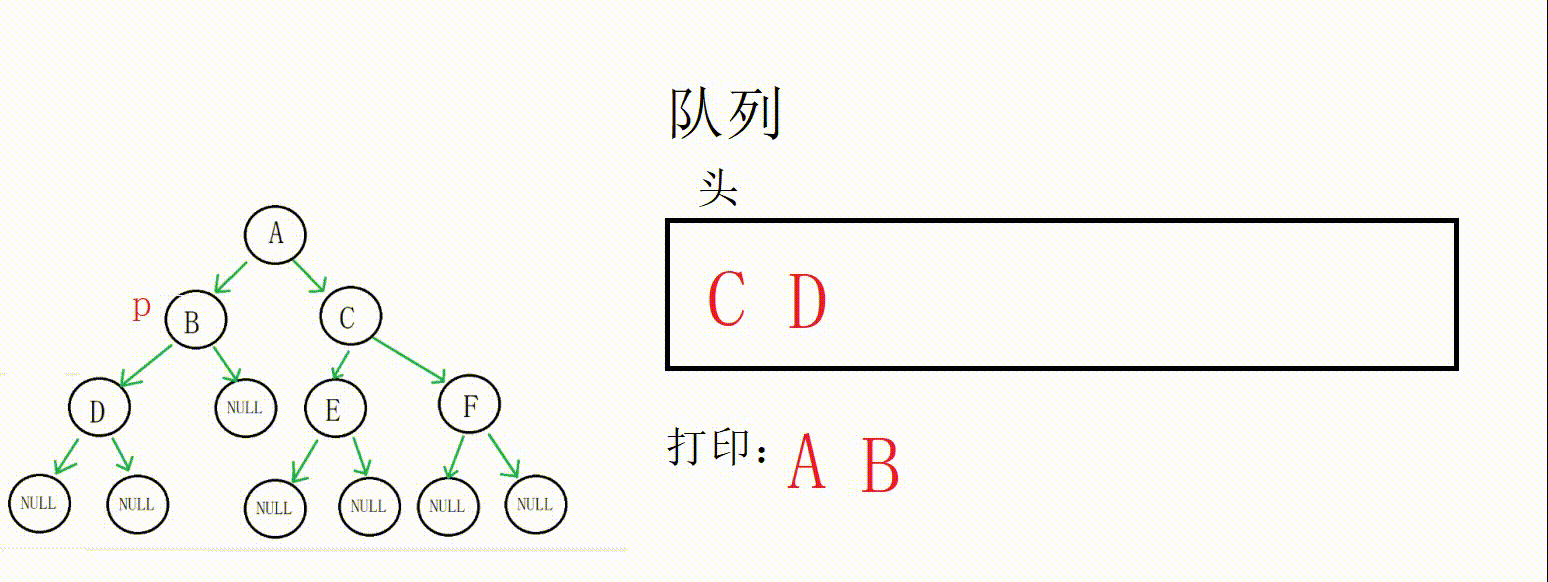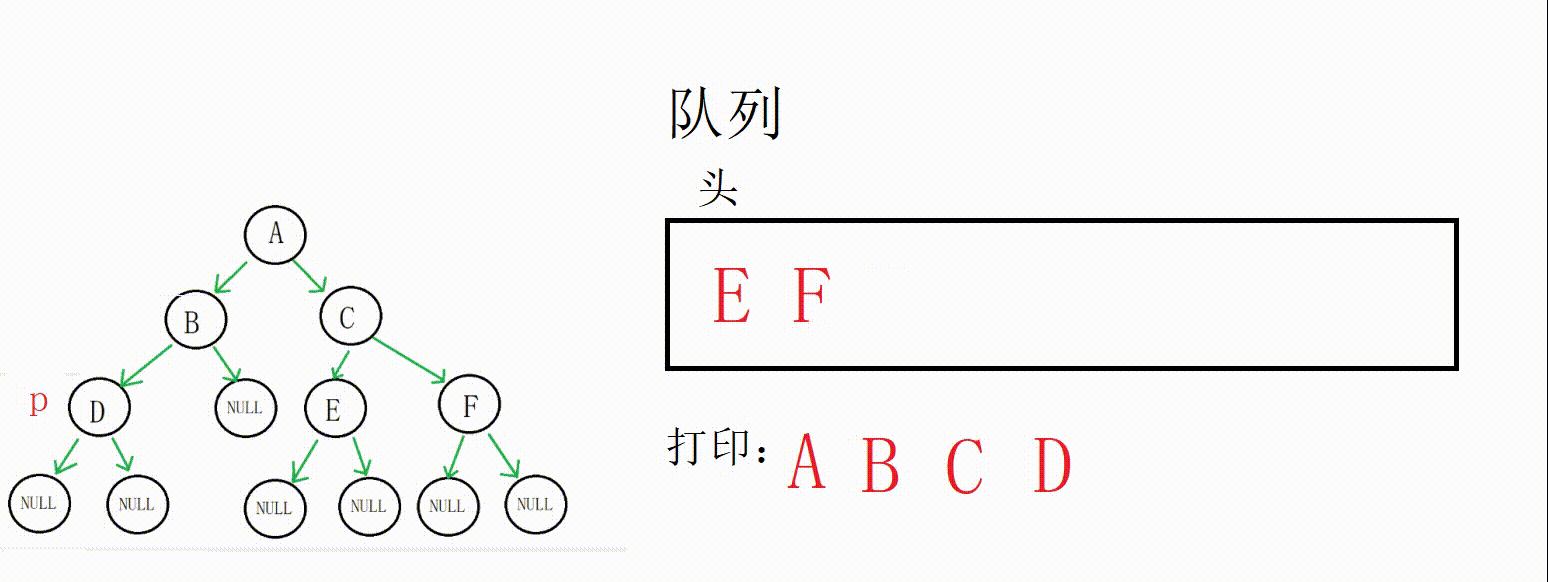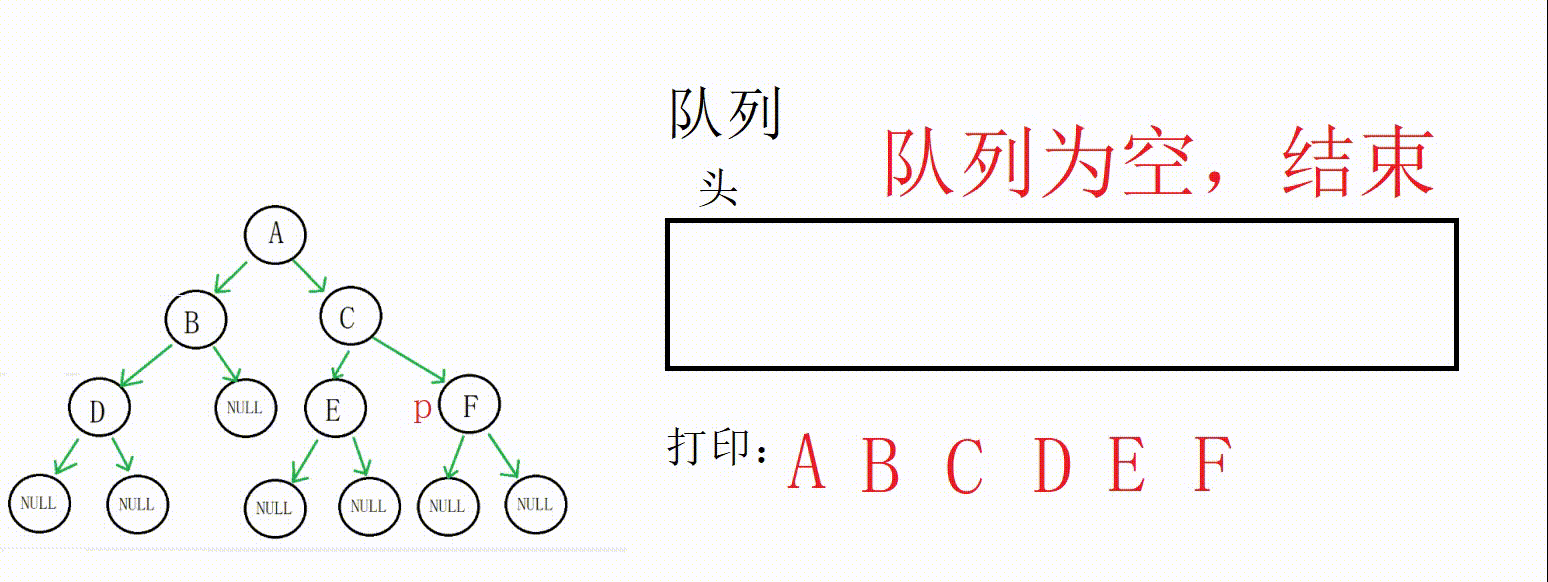
一开始把根节点放入队列中(如果为空树直接报错)

队列不为空，进入循环，取到A地址

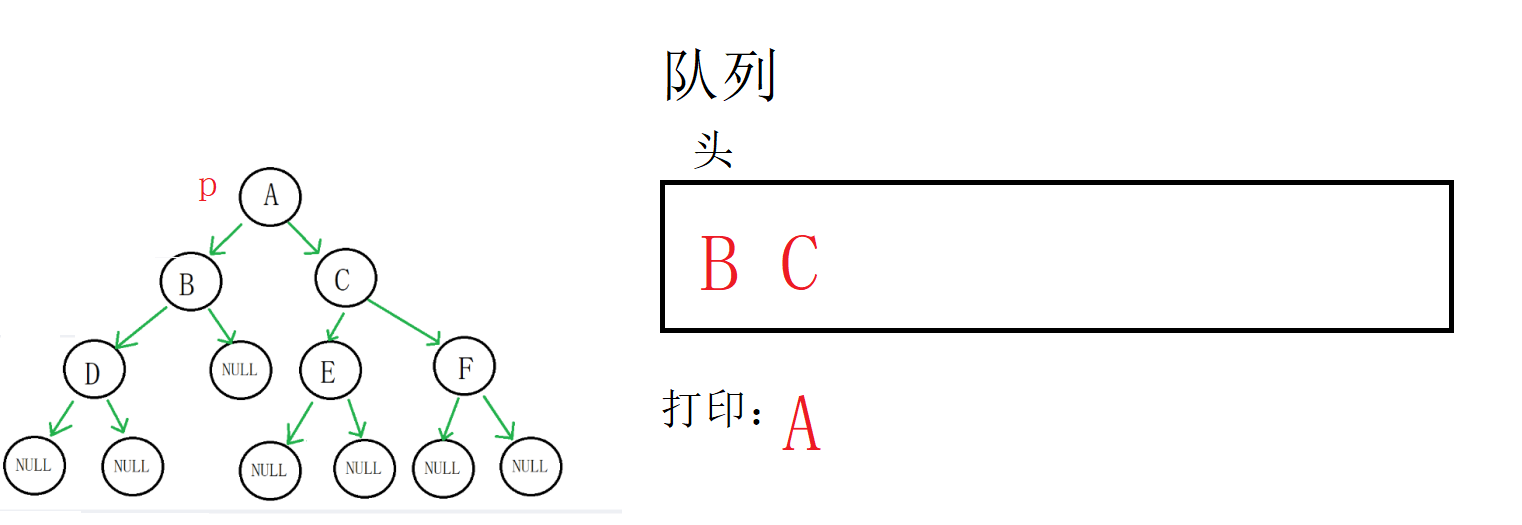
出队列，打印数据，A的左右孩子都不为空，入队列

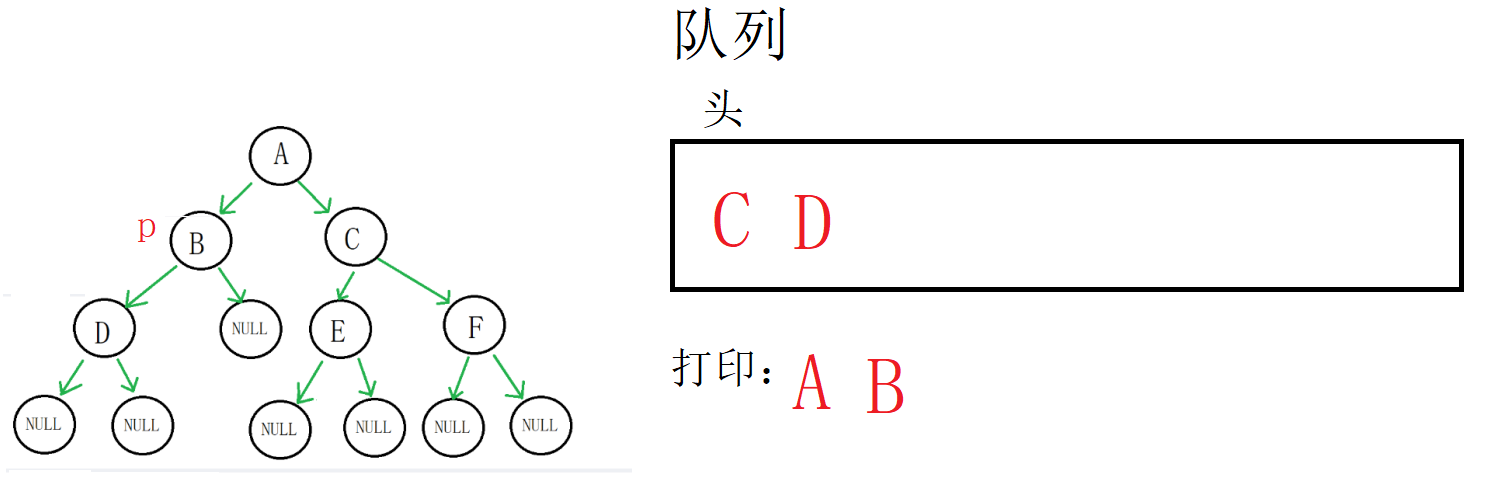
队列不为空，进入循环，取到B地址

出队列，打印数据，B的左孩子不为空，入队列

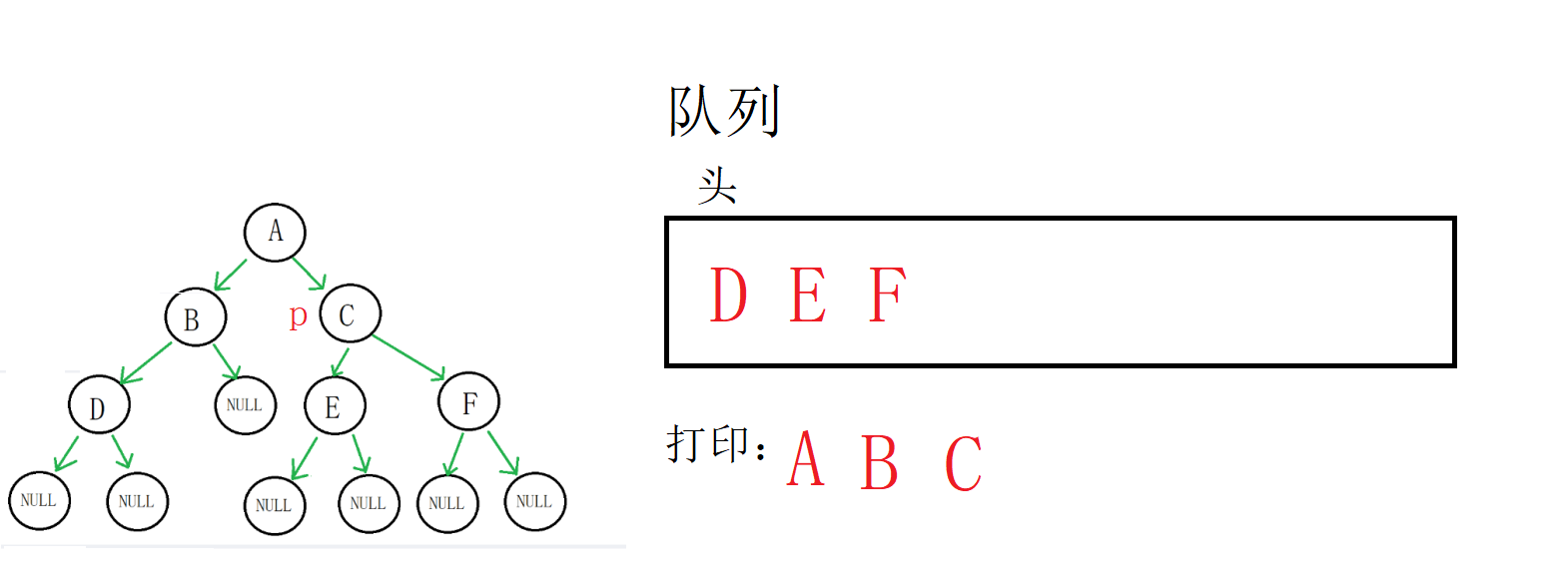
队列不为空，进入循环，取到C地址

出队列，打印数据，C的左右孩子都不为空，入队列

就这样循环一直到队列为空，层序遍历就完成了。

风语者！平时喜欢研究各种技术，目前在从事后端开发工作，热爱生活、热爱工作。

站长推荐