一. 区域和检索 - 数组不可变

• 题目链接：https://leetcode.cn/problems/range-sum-query-immutable/

1. 思路和代码

I. 博主的做法：

• 很简单，先在类里面整一个private数组，然后初始化它，只有就是简单的遍历求和。

class NumArray {
    private int[] nummber;
    public NumArray(int[] nums) {
        this.nummber = nums;
    }
    
    public int sumRange(int left, int right) {
        int sum = 0;

        for(int i = left; i <= right; i++)
            sum += nummber[i];

        return sum;
    }
}

II. 东哥的做法：

• 博主这样写，可以达到效果，但是效率很差，因为 sumRange 方法会被频繁调用，而它的时间复杂度是 O(N)，其中 N 代表 nums 数组的长度。
  
• 构建前缀和数组preSum，这样，sumRange 函数仅仅需要做一次减法运算，避免了每次进行 for 循环调用，最坏时间复杂度为常数 O(1)。

class NumArray {
    private int[] preSum;
    public NumArray(int[] nums) {
        preSum = new int[nums.length + 1];

        for(int i = 1; i < preSum.length; i++)
            preSum[i] = preSum[i-1] + nums[i-1];
    }
    
    public int sumRange(int left, int right) {

        return preSum[right + 1] - preSum[left];

        // return preSum[0];
    }
}

• • 这个技巧在生活中运用也挺广泛的，比方说，你们班上有若干同学，每个同学有一个期末考试的成绩（满分 100 分），那么请你实现一个 API，输入任意一个分数段，返回有多少同学的成绩在这个分数段内。那么，你可以先通过计数排序的方式计算每个分数具体有多少个同学，然后利用前缀和技巧来实现分数段查询的 API：

package LeetCode;

import java.util.*;

/**
 * @Author wangyichao
 * @date 2022/3/22 12:59
 * @Version 1.0
 * @Description
 */
public class Test {
	//前缀和数组	
    private  int[] preCount;
	
    public Test(int[] score){

        preCount = new int[score.length + 1];
		//初始化前缀和数组
        for(int i = 1; i < preCount.length; i++)
            preCount[i] = preCount[i-1] + score[i-1];
    }
    
	//统计分数段[left_core , right_core]中学生的个数
    public int sum(int left_core, int right_core){
        return preCount[right_core + 1] - preCount[left_core];
    }
    
	//使用计数排序(桶排序)，统计每一个分数的学生个数
    public static int[] add(int[] score){
        int[] num = new int[100 + 1];

        for(int score1 : score)
            num[score1]++;

        return num;
    }
    
    public static void main(String[] args) {

        Scanner sc = new Scanner(System.in);
        int left = sc.nextInt();
        int right = sc.nextInt();

        int[] score = add(new int[]{0,1,1,2,3,3,3,4,5});
        Test test = new Test(score);
        
        System.out.println(test.sum(left,right));
    }
}

2. 总结

• 博主本来想让 preSum[0] 来存储 sum 的值，最后发现结果不对，因为 preSum[0] 这个值也要参与到求和的运算当中。eg：求下标 0 ~ 下标 5 之间元素的和，那么就是 preSum[5 + 1] - preSum[0]。

二. 二维区域和检索 - 矩阵不可变

• 题目链接：https://leetcode.cn/problems/range-sum-query-2d-immutable/

1. 思路和代码

I. 博主的做法：

• 博主就是将二维数组的变成很多个一维数组，用多个一维数组构建前缀和数组。

class NumMatrix {
    private int[][] preMatrix;

    public NumMatrix(int[][] matrix) {
    	if(matrix.length == 0 || matrix[0].length == 0)
    		return;
        preMatrix = new int[matrix.length][matrix[0].length + 1];

        for(int i = 0; i < matrix.length; i++){
            for(int j = 1; j < preMatrix[0].length; j++){
                preMatrix[i][j] = preMatrix[i][j-1] + matrix[i][j-1];
            }
        }
    }
    
    public int sumRegion(int row1, int col1, int row2, int col2) {
        int sum = 0;

        for(int i = row1; i <= row2; i++)
            sum += preMatrix[i][col2 + 1] - preMatrix[i][col1];

        return sum;
    }
}

II. 东哥的做法：

• 类似于前缀和的做法， 先算出（0，0，row + 1，col + 1）这个大矩阵的和，也就是下图中绿色方框中的和，然后再减去剩下两个矩形的和，中间有一部分是多减的，现在把它加回来，最后得到了红色矩形的和，也就是我们想得到的结果。
  
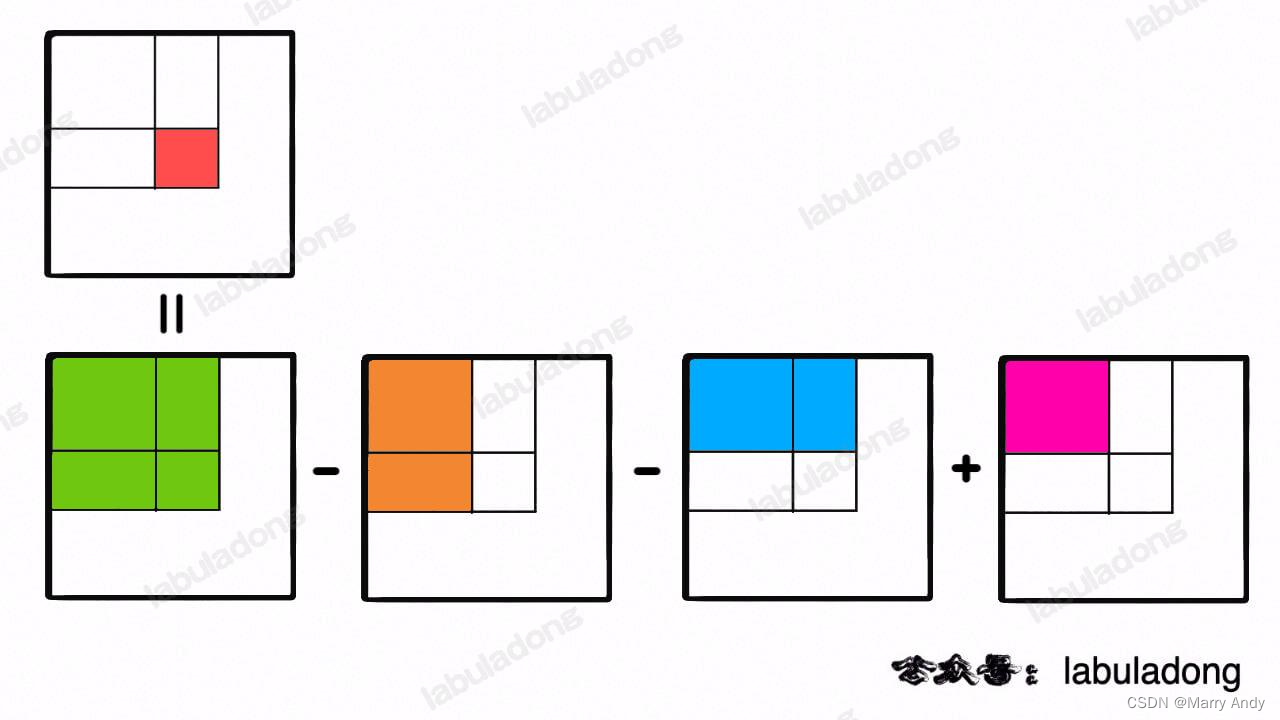
• 我们可以维护一个二维 preMatrix 数组，专门记录以原点为顶点的矩阵的元素之和，就可以用几次加减运算算出任何一个子矩阵的元素和。
• 这样，sumRegion 函数的时间复杂度也用前缀和技巧优化到了 O(1)，这是典型的「空间换时间」思路。

class NumMatrix {
    private int[][] preMatrix;

    public NumMatrix(int[][] matrix) {
        if(matrix.length == 0 || matrix[0].length == 0)
    		return;
        preMatrix = new int[matrix.length + 1][matrix[0].length + 1];

        for(int i = 1; i < preMatrix.length; i++){
            for(int j = 1; j < preMatrix[0].length; j++){
                preMatrix[i][j] = preMatrix[i-1][j] + preMatrix[i][j-1] + matrix[i-1][j-1] - preMatrix[i-1][j-1];
            }
        }
    }
    
    public int sumRegion(int row1, int col1, int row2, int col2) {


        return preMatrix[row2+1][col2+1] - preMatrix[row1][col2+1] - preMatrix[row2+1][col1] + preMatrix[row1][col1];
    }
}

这里preMatrix的构成还有最后的sumRegion都很迷，博主举个例子帮助大家理解：

score为输入的数组，preMatrix为前缀和数组。

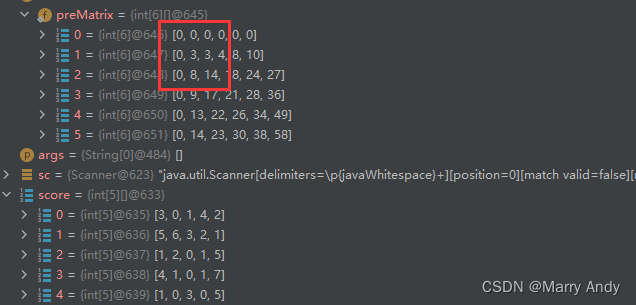
• 以preMatrix当中的14为例：

preMatrix[2][2] = preMatrix[1][2] + preMatrix[2][1] + matrix[1][1] - preMatrix[1][1]
14 (3 + 5 + 6) = 3 (0 + 3) + 8 (3 + 5) + 6 - 3
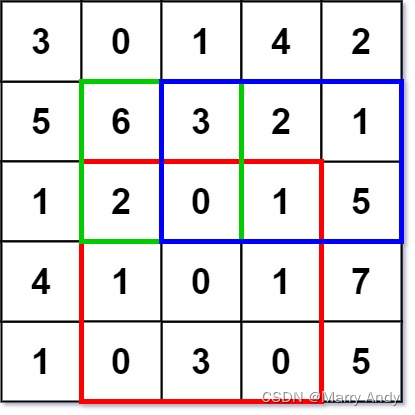
对应的Matrix如下图：

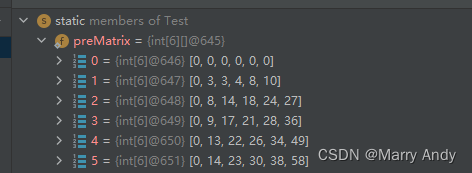
• 假设要算(1, 1, 2, 2)这个矩阵（黑色方框中矩形）的和：
  

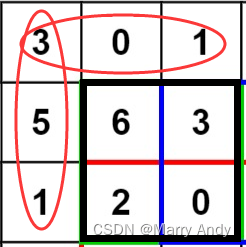
sum = preMatrix[3][3] - preMatrix[1][3] - preMatrix[3][1] + preMatrix[1][1]
11 = 21 (3 + 0 + 1 + 5 + 6 + 3 + 1 + 2 + 0) - 4 (3 + 0 + 1)- 9（3 + 5 + 1） + 3

• 本质上还是矩阵的相互加减

2. 总结

• 博主的那个方法，虽然是前缀数组的衍生，但sumRegion时间复杂度为O(n)，而东哥的这个时间复杂度为O(1)。
• 很巧妙，运用迭代的思想构建preMartix数组，又运送矩阵相减的方法，算出sum，东哥牛逼！！！！
  -二维数组.length 返回的是二维数组行的个数，而列的个数要用二维数组[0].length来表示。
• 一维数组中，只有第一个元素是空的；二维数组中，第一行第一列都是空的。发现一个规律：preMatrix的行数列数都减一就是matrix中对应的矩阵(0, 0, row, col)右下角点的坐标
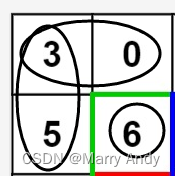
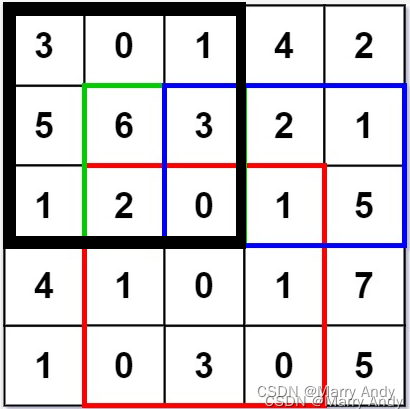
  • eg：以上面那个例子接着来说，preMatrix[3][3]： (2 ,2)即是大矩阵右下角的坐标，那么整个大矩阵就是（0, 0, 2, 2）,也就是下面这个图
    

参考：https://labuladong.github.io/algo/di-yi-zhan-da78c/shou-ba-sh-48c1d/xiao-er-me-03265/