ps. 本章只介绍有向图和无向图。

目录

图的定义

有向图和无向图

图的概念

图的存储

图的基本操作

图的定义

图（Graph）是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G(V,E)

- G 表示一个图，

- V（Vertex）表示顶点的有穷非空集合，

- E 表示图中边（Edge）的集合。

有向图和无向图

如果一个图是由单向链表所连接，即它的边是有顺序的配对，那么该图是一个有向图(directed graph)。反之，则称为无向图(undirected graph)。

下图中（a）为无向图，（b）为有向图。（可以简单的理解为，有箭头指向方向的就是有向图，反之是无向图）

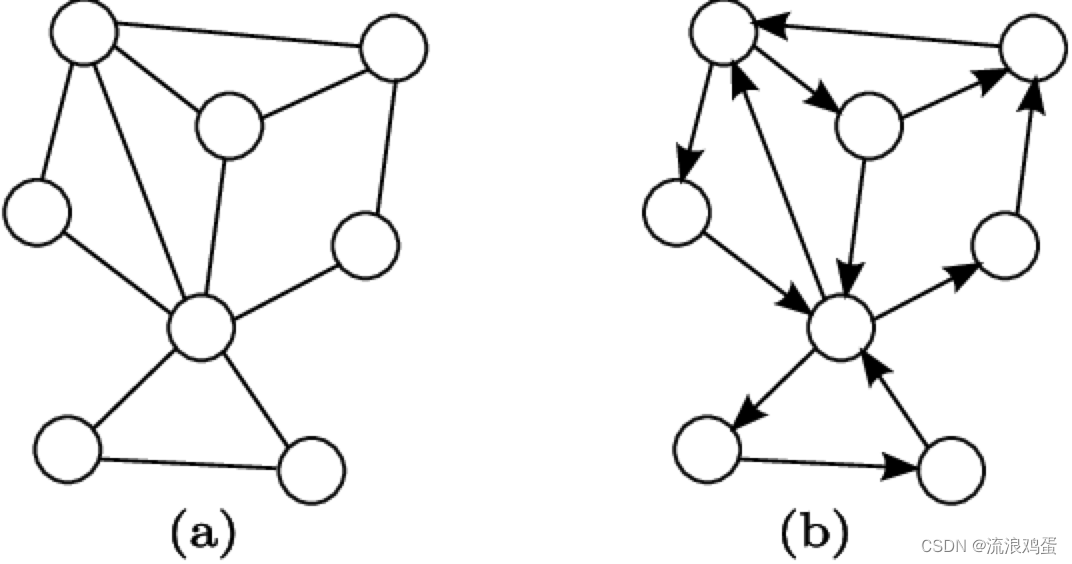
图的概念

1. 路径（Path）：从一个顶点Vi到另外一个顶点Vj的边的序列被称为一个路径。

2. 环（Cycles）： 一条路径的起始顶点和结束顶点是同一个且通过不重复的路径的组合的话，称为一个环。如果一个图中有环的结构，它就被称为一个有环图(cyclic graph)，反之则是无环图(acyclic graph)。

3. 连通（Connected）：如果从Vi到Vj有路径可通，则称顶点Vi和顶点Vj是连通的。

4. 子图 （Subgraphs）： 有一个图 G =（V，E）， 另外一个 S =（U，F），若 U ∈ V ∧ F ∈ E 且 S ≤ G，S就是G的子图（当S是G的一部分时，S就是G的子图）

5. 顶点的度 （Degree）：在有向图中，对于一个顶点v，指向v的边的数量就是这个顶点的入度(in-degree)，从v指向其它顶点的边的数量，就是这个顶点的出度(out-degree)。 在无向图中，由于边不存在方向，所以不谈入度和出度，只谈度(degree),也就是包含这个顶点的边的总数量。

6. 权（Weight）：有些图的边或弧具有与它相关的数字，这种与图的边或弧相关的数叫做权。

图的存储

图结构除了要存储本身的顶点数据以外，还得存储不同顶点之间的关系，因此图的存储相对复杂，常用的图的存储结构有邻接矩阵和邻接表等。

1. 邻接矩阵：

图的邻接矩阵（Adjacency Matrix）存储方式是用两个数组来表示图。一个一位数组存储图中顶点信息，一个二维数组（称为领接矩阵）存储图中的边或弧的信息。

对于无向图：

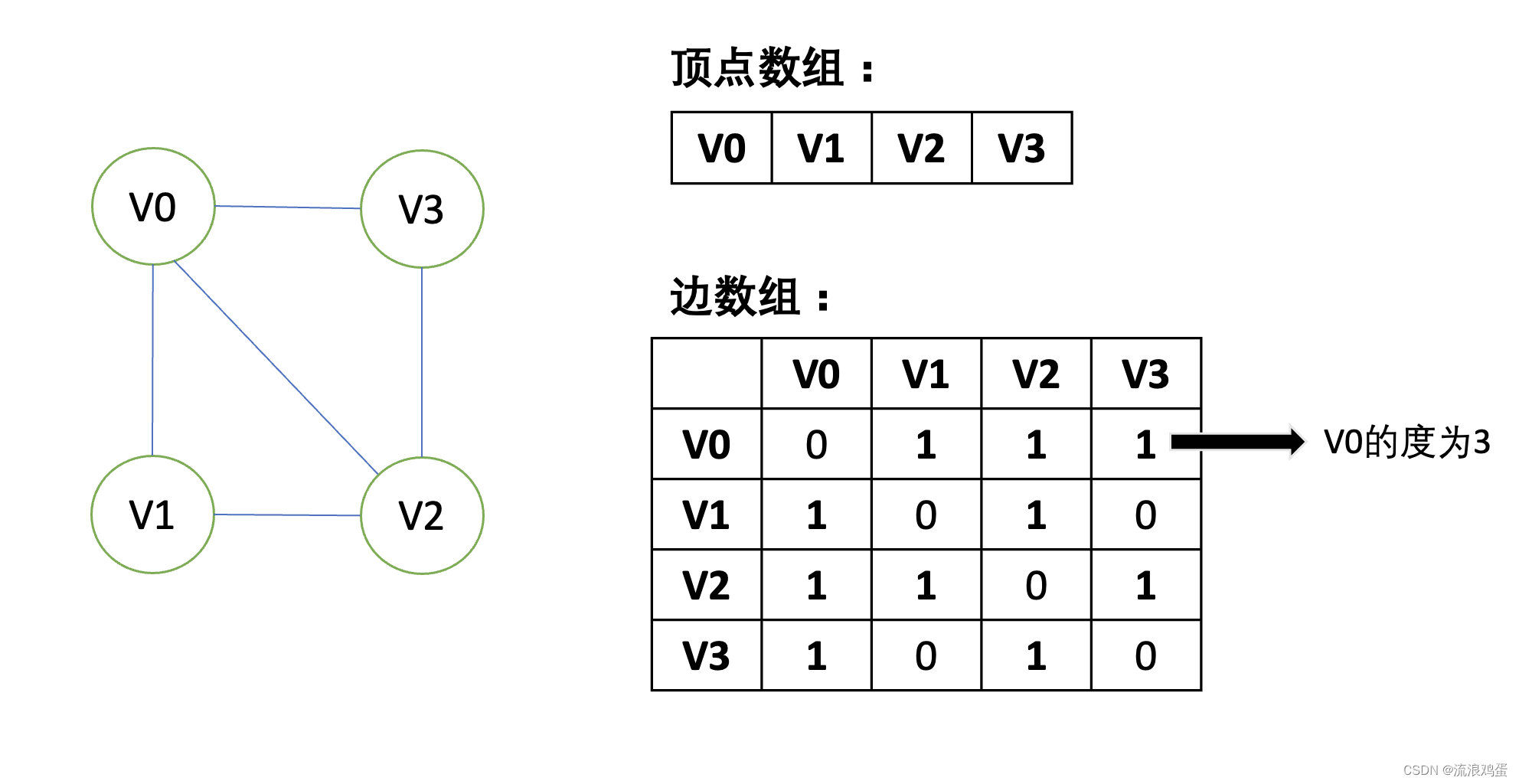
可以看出来V1到V3是不连通的，左边的边数组表示了顶点与顶点之间的关系（1代表两个顶点之间连通，0代表不连通），且不论行的和或者列的和都可以反映出来顶点的度数。（前面提到了无向图不分出入度）

对于有向图：

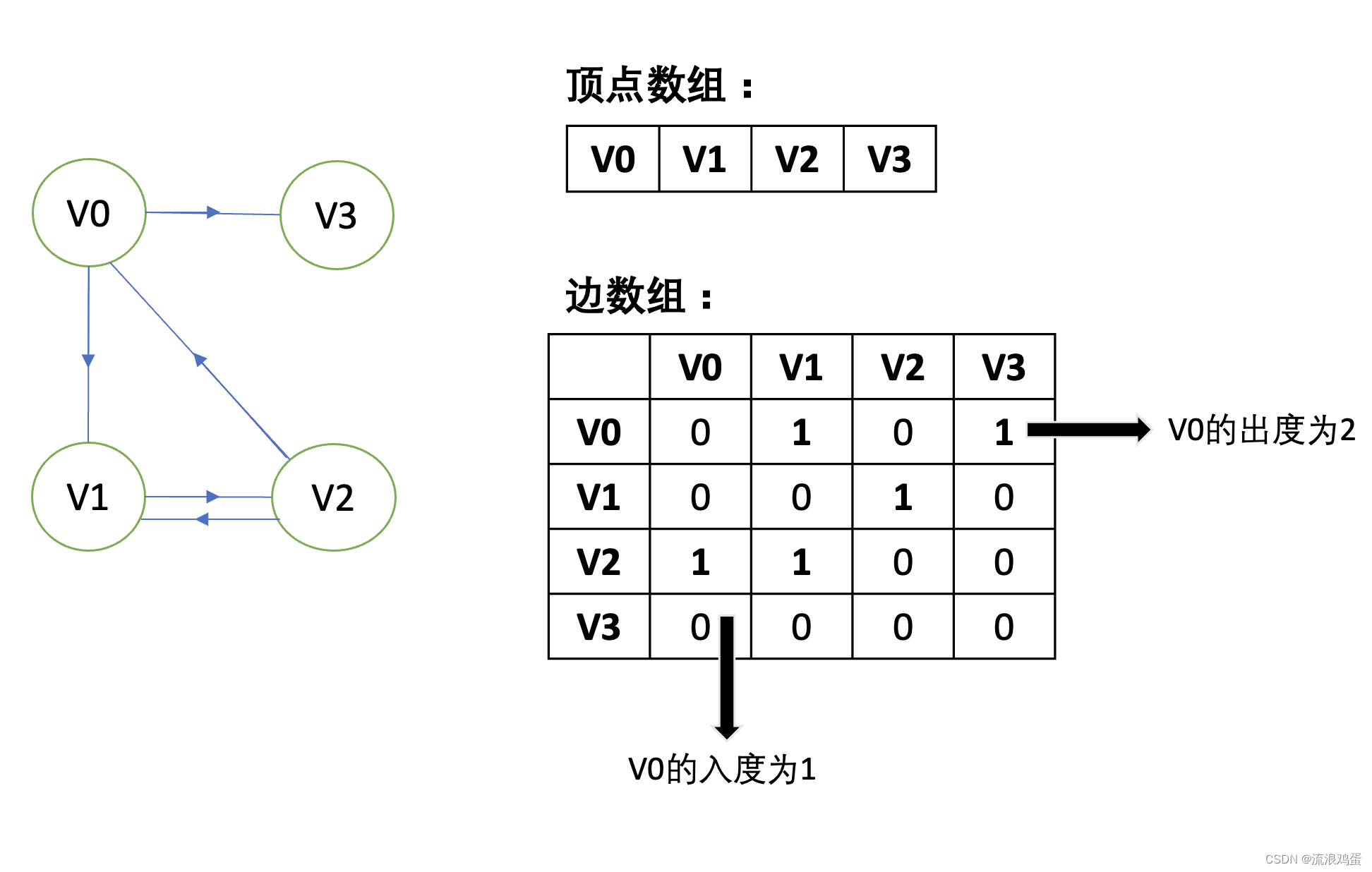
可以看出来V1和V3也是不连通，且V2和V3也不连通，左边的边数组也反应出来了，但与无向图不同的是，它的列的和代表入度，行的和代表出度。

邻接矩阵的优点：

1. 查询边的存在和权重高效：可以直接通过查找矩阵中对应的元素来判断两个顶点之间是否存在边，以及获取边的权重，时间复杂度为O(1)。
2. 结构简单：邻接矩阵易于实现，可以使用二维数组来表示。

邻接矩阵的缺点：

1. 空间效率较低：邻接矩阵需要为图中每对顶点分配空间，因此在稀疏图（边数相对较少的图）中，邻接矩阵可能会浪费大量空间。对于具有n个顶点的图，邻接矩阵的空间复杂度为O(n^2)。
2. 查询相邻顶点效率较低：查找与某个顶点直接相邻的所有顶点需要遍历该顶点所在行或列的所有元素，时间复杂度为O(n)。

2. 邻接表：

邻接表（Adjacency list）由表头节点和表节点两部分组成，图中每个顶点均对应一个存储在数组中的表头节点。如果这个表头节点所对应的顶点存在邻接节点，则把邻接节点依次存放于表头节点所指向的单向链表中。

对于无向图：

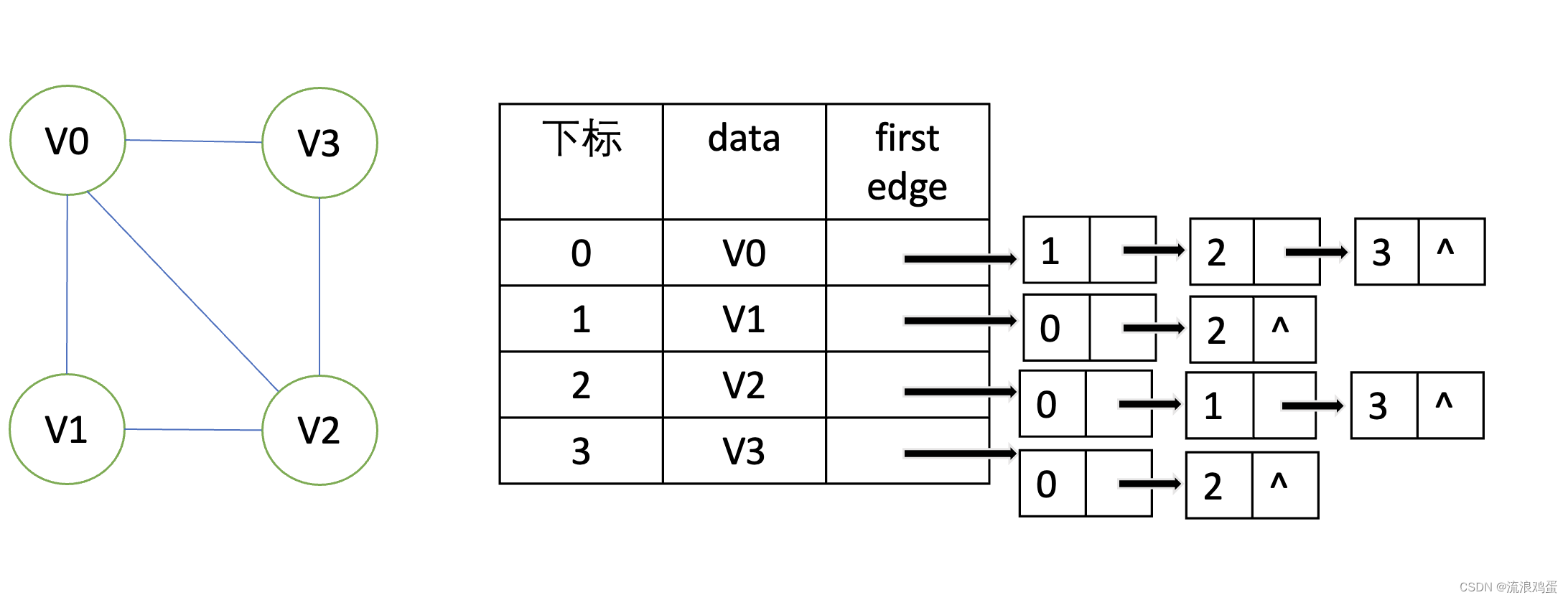
对于有向图：

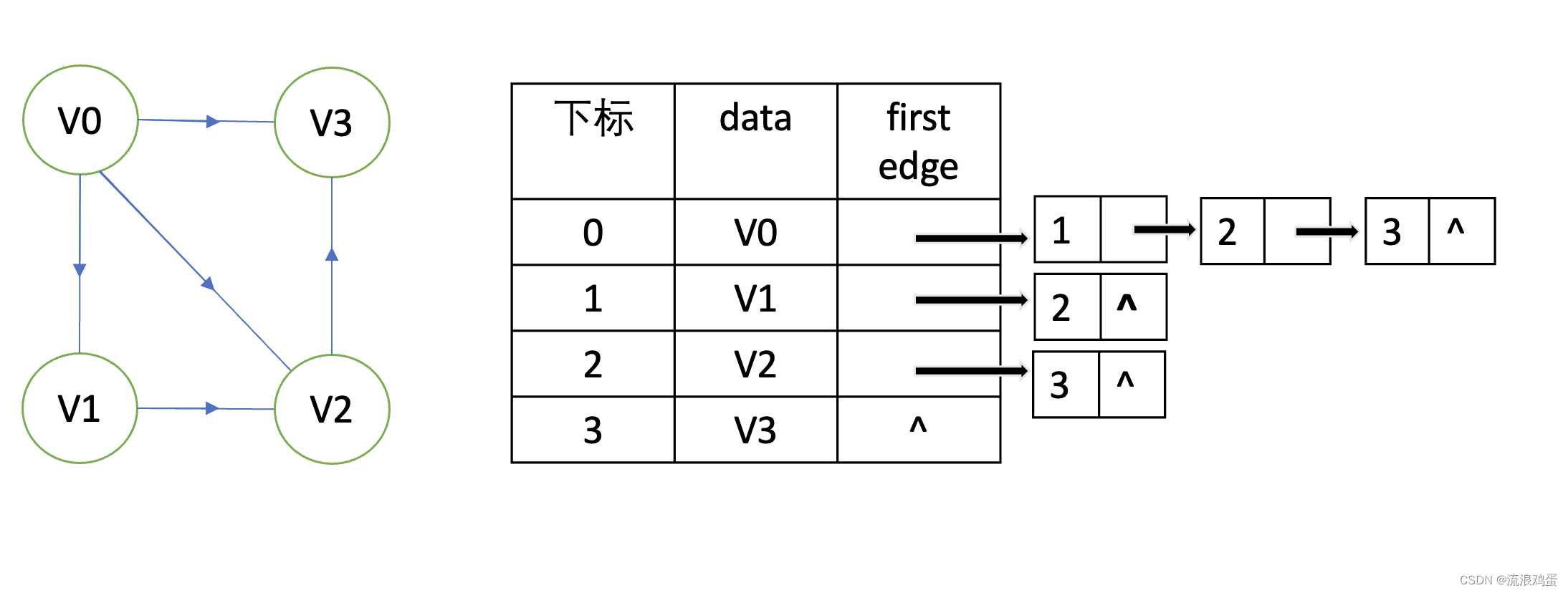
邻接表的优点：

1. 空间效率：邻接表只存储图中实际存在的边，因此在稀疏图（边数相对较少的图）中，邻接表比其他表示方法（如邻接矩阵）更节省空间。
2. 查询相邻顶点高效：查找与某个顶点直接相邻的所有顶点只需访问该顶点对应的列表，时间复杂度与相邻顶点数成正比。

邻接表的缺点：

1. 查询两个顶点之间是否存在边的效率较低，因为需要遍历其中一个顶点的邻接表来查找另一个顶点。

图的基本操作

numVertices()：返回图的顶点总数。

numEdges()：返回图的边的总数。

getVertex(u)：如果存在一个顶点u，则返回这个顶点，否则返回null。

getEdge(u, v)：如果存在一条从顶点u到顶点v的边，则返回这条边，否则返回null。

insertVertex(x)：创建并返回一个新的顶点且存储在x节点中。

insertEdge(u, v, x)：创建并返回一个新的从顶点u到顶点v的边，且存储在x节点中。

removeVertex(v)：从图中移除掉顶点v和与其相关的边。

removeEdge(e)：从图中移除掉边e。

这篇文章就到这结束了，当然还有许多知识点没有涉及到（等之后慢慢补上），但图的定义，概念，存储方式和基本操作都有讲到，要是有什么错误欢迎各位大佬指出。

下篇文章会讲深度/广度优先搜索。