您现在的位置是：首页 >技术教程 >数据结构各结构特点（数组、链表、栈、队列、树）网站首页技术教程

目录

 一、数组

二、链表

三、栈

四、队列

五、树

1.二叉树

2.二叉查找树

3.平衡二叉树（AVL树）

4.红黑树

 六、总结：

1.红黑树和平衡二叉树的区别：

2.为什么有了数组和链表还要引入二叉树？

3.为什么有了二叉树还要引入平衡二叉树？

4.为什么有了平衡二叉树还要引入红黑树？

---

 一、数组

简介：

数组是一种线性表结构，元素序列有序，在内存中开辟一段连续的内存空间。数组具有随机访问的优势，可以通过下标访问元素，时间复杂度为O(1)，但插入删除操作比较复杂，需要移动其他元素，所以时间复杂度为O(n)。

特点：

1.数组在逻辑上、内存中都是连续的，数组需要开辟一段连续的内存空间

2.查找元素快：通过索引，可以快速访问指定位置的元素

3.增删元素慢：因为数组长度是固定的，如果插入删除元素的话，就要涉及到元素的移动。

缺点：

1.插入删除操作所需要移动的元素很多，效率低下。

2.数组在内存中是一段连续的内存空间，所以必须为数组开辟足够的空间，否则有溢出的风险。

二、链表

简介：

链表也是一种线性表结构，但它在内存中不一定是连续的。即逻辑上连续，物理存储结构上不连续，大小不固定。

链表基于指针实现，它的存储单元以结点为单位，每一个结点由数据域和指针域组成。

数据域：存储数据元素信息的域

指针域：存储直接后继位置的域。

遍历链表需要从头结点开始依次往后遍历，每个节点只有一个前驱结点，每个节点只有一个后继结点，首结点没有前驱结点，尾结点没有后续结点。

特点：

1.通过指针的形式将一组存储单元联系在一起的数据结构

2.逻辑上连续，物理存储结构上不连续，大小不固定

3.单链表维护一个单向的指针，通过指针寻找下一存储单元；双链表维护一个双向的指针，通过指针可以寻找上一存储单元和下一存储单元。

4.查找元素慢：链表没有索引，所以查找元素需要从头结点开始依次遍历链表

5.增删元素快：链表通过指针相连接，增删元素只需要修改指针指向即可，不需要涉及元素的移动。

单链表、双链表概念及基本功能的代码实现：

单链表的基本操作

双链表的基本操作

三、栈

概念：

栈（stack）是一个后进先出（FILO-First In Last Out）的有序列表，允许插入和删除的一端为变化的一端，称为栈顶（Top），另一端为固定的一端，称为栈底（Bottom）。

先放入到栈的元素在栈底，后放入栈的元素为栈顶。栈顶的元素先出，栈底的元素后出。

 可以使用单链表和数组的方式实现栈。

单链表：每次插入都将元素插入到第一个位置，每次获取结点都从链表头部获取。

数组：每次插入元素都放在数组的尾部，每次获取元素也从数组尾部获取即可。

栈的概念及基本功能的代码实现：

栈的基本操作

四、队列

概念：

队列（Queue）是一个先进先出（FIFO-First In First Out）的有序列表，主要方法有入队（enqueue / offer）和出队（dequeue / poll）

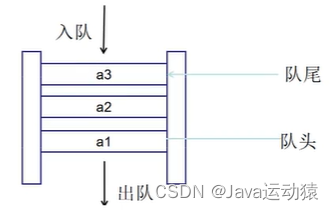
可以使用单链表和数组的方式实现队列。

单链表：每次入队都将元素插入到链表尾部，每次获取结点都从链表头部获取。

数组：每次入队都将元素按顺序依次添加，每次出队都从数组前面依次出去。

队列的概念及基本功能的代码实现：

队列的基本操作

五、树

树的概念及基本功能的代码实现：

树的基本概念

1.二叉树

概念：

二叉树是每个节点最多有两个子树的树结构，也就是说树的度为2。正常情况下，左子树的结点值比父节点小，右子树的结点值比父节点大。二叉树具有很好的搜索性能，可以实现二分查找。

为什么会出现二叉树：因为二叉树，可以使用二叉法，当数据量较大的时候，比链表查询和插入效率更高，因为相同的数据量的情况下，二叉树深度一定比链表的深度小。所以查询的深度就小，所以比较节省时间

二叉树的缺点：二叉树可能会有极端的情况，就是某个节点的深度无限大，这样的二叉树和链表没啥区别，于是为了限制二叉树极端的情况，满足二叉树深度较小的情况，介继而推出了平衡二叉树。

二叉树遍历的方式：

前序遍历：根节点 -> 左节点 ->右节点

中序遍历：左节点 -> 根节点 -> 右节点

后续遍历：左节点 -> 右节点 -> 根节点

层次遍历：从根节点开始，一层一层往下遍历（采用队列来实现，将根节点放入队列中，然后出列，响应地将其左右子节点放入队列中，以此类推。）

满二叉树和完全二叉树：

满二叉树：每一层的结点数都达到最大值。

完全二叉树：若设二叉树的深度为k，除第k层外，其他各层（1~k-1）的结点数都达到最大个数，第k层所有的结点都连续集中在最左边，这就是完全二叉树。

 注：完全二叉树的话，所有的结点都连续集中在最左边，也就是如下图所示，右子节点可以没有，但如果右子节点有的话，则左子节点必须存在。下图中如果叶子结点只有4结点，5、6、7结点没有的话，也是完全二叉树。

二叉树的概念及基本功能的代码实现：

二叉树概念及基本功能实现

2.二叉查找树

概念：

二叉查找树，即左子树结点值都小于根节点，右子树结点值都大于根节点。同时具有数组的查询效率，链表的增删改效率。

通过中序遍历方式可以将二叉查找树按从小到大的方式将树各节点的值打印出来。

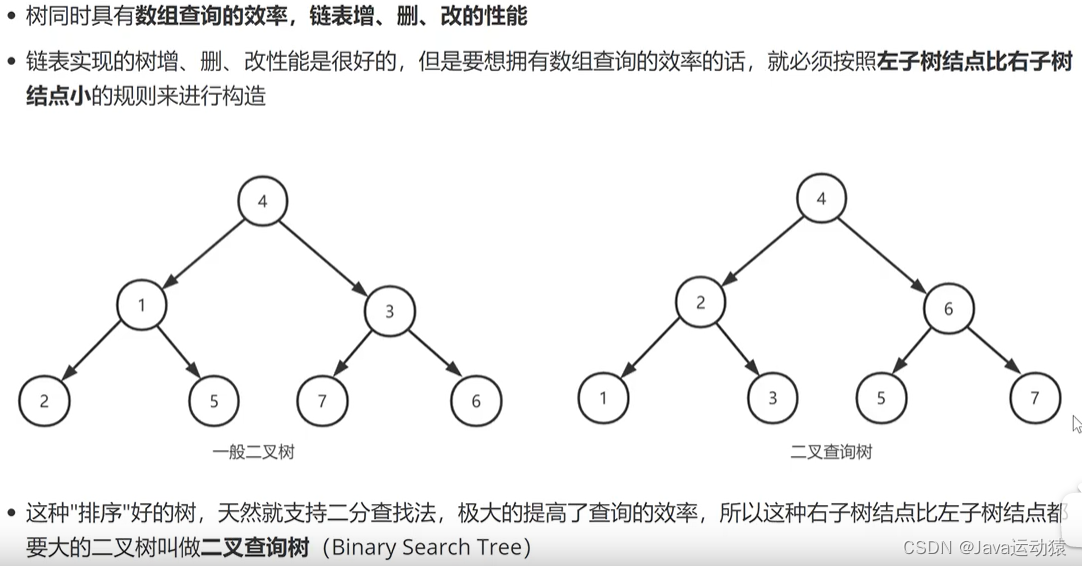
特点：

1.二叉查找树左子树的所有节点的值都小于父节点的值， 右子树的所有节点的值都大于父节点的值。

2.具有数组的查询效率，也具有链表的增删改性能。

 缺点：

二叉查找树的规则只要是左子树小于右子树即可，但可能会出现“一边倒”的情况，那么二叉查找树就退化成链表了，二叉查找树的查询优势也无法体现出来了。

二叉查找树的概念及基本功能的代码实现：

 二叉查找树

3.平衡二叉树（AVL树）

概念：

平衡二叉树也称AVL树，主要是为了解决二叉查询树不平衡的情况下，导致查询效率低下的解决方案。二叉查找树极端情况下会出现一边倒的情况，平衡二叉树就是为了解决这一问题，通过左旋、右旋的方式，保证树的平衡。

特点：

1.拥有二叉查找树的全部特性

2.左子树和右子树的高度差绝对值不超过1

3.插入和删除数据时需要进行平衡操作，即左旋、右旋的方式，来保证树的平衡

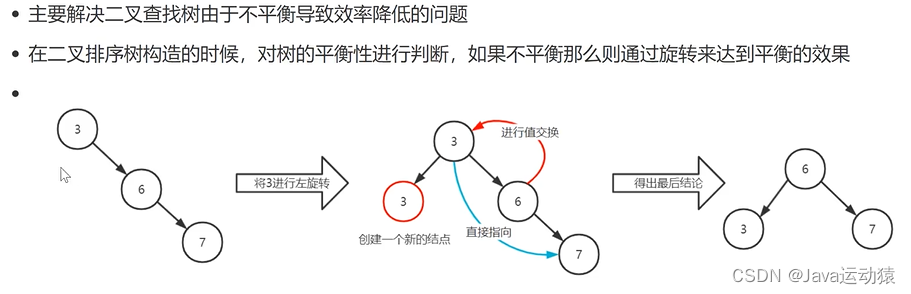
优缺点:

平衡二叉树保证了不会出现一边倒的情况， 通过左旋、右旋来保证了二叉树的平衡，把插入、删除、查找的时间复杂度最好和最坏情况都维持在O（logN）。但平衡二叉树这种高度差为1的要求太严格了，尤其是对于频繁删除、插入的场景非常浪费时间。

 平衡二叉树的概念及基本功能的代码实现：

平衡二叉树（AVL树）

4.红黑树

概念：

红黑树也是一种对查询效率进行优化的二叉查找树，它要求从根节点到叶子结点的最长可能路径不多于最短的可能路径的两倍长。

红黑树的特点：

• 具有二叉树所有特点。
• 每个节点只能是红色或者是黑色。
• 根节点只能是黑色，且黑色根节点不存储数据。
• 任何相邻的节点都不能同时为红色。
• 红色的节点，它的子节点只能是黑色。
• 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

 六、总结：

1.红黑树和平衡二叉树的区别：

（1）红黑树放弃了追求完全平衡，而是追求大致平衡，在与平衡二叉树的时间复杂度相差不大的情况下，保证每次插入最多两次旋转，删除最多三次旋转就能达到平衡，实现起来也更为简单。

（2）平衡二叉树追求绝对平衡，条件比较苛刻，实现起来比较麻烦，每次插入新节点之后需要旋转的次数不能预知。

所以，对于插入、删除操作较多的情况下，红黑树的效率是优于平衡二叉树的；而对于插入、删除不频繁，只是对查找要求较高，那么平衡二叉树还是较优于红黑树。

2.为什么有了数组和链表还要引入二叉树？

针对数组和链表的优缺点，无法说链表一定优于数组，或者是数组一定优于链表，因为某些长期的需要，数组在查询方面效率高，链表在插入、删除方面效率高，所以就推出一个相对折中的二叉树。二叉树在插入、删除、查询方面效率都较好。

3.为什么有了二叉树还要引入平衡二叉树？

有了二叉树还不算完，二叉树有一种极端的情况，就是所有的子结点偏向一端，二叉树退化成链表，这就相当于我选择了这种的二叉树，你现在罢工不干了，找了个链表来糊弄我...

所以为了解决二叉查找树退化为链表的情况，引入了平衡二叉树，即：

平衡二叉树是为了解决二叉树退化成一棵链表而诞生的。

4.为什么有了平衡二叉树还要引入红黑树？

实际使用过程中，因为平衡二叉树追求绝对严格的平衡关系，显然这个规则在于频繁的插入、删除等操作的情景性能肯定会出现问题...

所以为了解决这个问题，进而又引入了红黑树。

平衡二叉树追求绝对严格的平衡，平衡条件必须满足左右子树高度差不超过1，红黑树是放弃追求完全平衡，它的旋转次数少，插入最多两次旋转，删除最多三次旋转，所以对于搜索、插入、删除操作较多的情况下，红黑树的效率是优于平衡二叉树的。