您现在的位置是:首页 >技术杂谈 >深度学习架构-Tensorflow网站首页技术杂谈
深度学习架构-Tensorflow
深度学习基本概念
- 人工智能是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。人工智能的目的 就是让计算机能够像人一样思考。
强人工智能:就是要使机器学习人的理解、学习和执行任务的能力。
弱人工智能:指用于自动化特定任务的软件。 - 机器学习的广义概念:是指从已知数据中获得规律,并利用规律对未知数据进行预测的方法。机器学习是一种统计学习方法,机器人和计算机等机器需要使用大量数据进行学习,从而提取出所需的信息。
- 深度学习 就是一种利用深度人工神经网络来进行自动分类、预测和学习的技术。
- 人工智能>机器学习>深度学习
TensorFlow
TensorFlow 是一款用于数值计算的强大的开源软件库,特别适用于大规模机器学习的微调。
- MNIST数据读取、建模、编译、训练、测试
import tensorflow as tf
# 载入数据
mnist = tf.keras.datasets.mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
# 建模
model = tf.keras.models.Sequential([
tf.keras.layers.Flatten(input_shape=(28, 28)), # 将输入“压平”,即把多维的输入一维化,只有第一层有输入数据的形状
tf.keras.layers.Dense(128, activation='relu'), # 该层的输出维度或神经元个数和激活函数
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Dense(10, activation='softmax')
])
# 编译(优化器、损失和评价)
model.compile(optimizer='adam',loss='sparse_categorical_crossentropy',metrics=['accuracy'])
# 训练(训练和验证数据不一样)
model.fit(x_train, y_train, epochs=5)
# 验证
model.evaluate(x_test, y_test, verbose=2)
- 优化器 tf.optimizers;
SGD 随机梯度下降优化器
tf.keras.optimizers.SGD( learning_rate=0.01, momentum=0.0,nesterov=False, name='SGD', **kwargs)
学习率、动量、是否使用nesterov震荡
Adam优化器
tf.keras.optimizers.Adam(learning_rate=0.001)
- 损失函数:均方根误差MSE(MeanSquaredError)、二值交叉熵(BinaryCrossentropy);
metrics sparse_categorical_crossentropy(多分类损失函数) - metrics评价函数
“accuracy” :真实值(y_)和预测值(y) 都是数值;
“sparse_accuracy”:y_和y都是以独热码和概率分布表示;
“sparse_categorical_accuracy”:y_是以数值形式给出,y是以独热码给出 - 数据结构
1)Rank:维度
2)Shape:每个维度数据的个数
3)Data type:bool、int、float、string、complex、Truncated float、Quantized int
4)Variables与Constant : 变量和常数
常用函数
- 数据类型转换
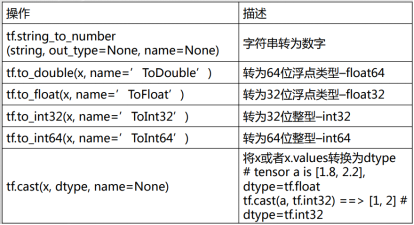
import tensorflow as tf
import tensorflow.compat.v1 as tf1
string = '12.3'
n1 = tf1.string_to_number(string, out_type=None, name=None) #字符串转为数字
x = 12.3
d1 = tf1.to_double(x, name='ToDouble')#转为64位浮点类型float64
f1 = tf1.to_float(x, name='ToFloat') #转为32位浮点类型float32
i1 = tf1.to_int32(x, name='ToInt32') #转为32位整型int32
i2 = tf1.to_int64(x, name='ToInt64') #转为64位整型–int64
a = [1.8, 2.2]
i3 = tf.cast(a, tf.int32) # 将a或者a.values转换为dtype
- 形状操作
t = [ [[1, 1, 1], [2, 2, 2]] , [[3, 3, 3], [4, 4, 4]] ]
tf.shape(t) #返回维度中数据的个数
tf.size(t) #返回数据的元素数量
tf.rank(t) #返回数据维度
t = [1, 2, 3, 4, 5, 6, 7, 8, 9]
print(tf.shape(t))
t2 = tf.reshape(t, [3, 3]) #改变tensor的形状
print(tf.shape(t2))
t3 = tf.reshape(t, [3, -1])
print(t3)

- 其它操作函数
t = [2,3] #插⼊维度1进⼊⼀个tensor中
t1 = tf.shape(tf.expand_dims(t, 0)) [1,2]
t2 = tf.shape(tf.expand_dims(t, 1)) [2,1]
t3 = tf.shape(tf.expand_dims(t, -1)) [2,1]
t4 = tf.ones([2,3,5]) #用数字1填充所有维度
t6 = tf.shape(tf.expand_dims(t4, 2)) shape=【2,3,1,5】
t= [[[1, 1, 1], [2, 2, 2]],[[3, 3, 3], [4, 4, 4]],[[5, 5, 5], [6, 6, 6]]]
#对tensor进⾏切⽚操作
t1 = tf.slice(t, [1, 0, 0], [1, 1, 3])
t2 = tf.slice(t, [1, 0, 0], [1, 2, 3])
t3 = tf.slice(t, [1, 0, 0], [2, 1, 3])
t = tf.ones([5,30])
t1, t2, t3 = tf.split(t,3,1) #沿着某⼀维度将tensor分离
print(tf.shape(t1))
print(tf.shape(t2))
print(tf.shape(t3))
t1 = [[1, 2, 3], [4, 5, 6]]
t2 = [[7, 8, 9], [10, 11, 12]]
t3 = tf.concat([t1, t2], 0) #沿着某⼀维度连结tensor
t4 = tf.concat([t1, t2], 1)
x = [1, 4] y = [2, 5] z = [3, 6]
t1 =tf.stack([x, y, z]) #沿着第⼀维stack [[1 4] [2 5] [3 6]]
t2 = tf.stack([x, y, z], axis=1) #axis取0时表示按x轴叠加,取1时表示按y轴叠加#[[1 2 3] [4 5 6]]
t = [[ [[ 0, 1, 2, 3],[ 4, 5, 6, 7],[ 8, 9, 10, 11]],
[[12, 13, 14, 15],[16, 17, 18, 19],[20, 21, 22, 23]] ]] # shape=(1,2,3,4),dims = [3]
t1 = tf.reverse(t, dims) #沿着某维度进⾏序列反转dims = [1]
t2 = tf.reverse(t, dims) #dims = [2]
t3 = tf.reverse(t, dims) [[ [[ 8 9 10 11] [ 4 5 6 7] [ 0 1 2 3]] [[20 21 22 23] [16 17 18 19] [12 13 14 15]] ]]
t = [[1, 2, 3],[4, 5, 6]]
t1 = tf.transpose(t) #调换tensor的维度顺序
t2 = tf.transpose(t, perm=[1, 0]) # [[1 4] [2 5] [3 6]]
indices = [0, 1, 2] depth = 3
t1 = tf.one_hot(indices, depth) #
indices = [0, 2, -1, 1] depth = 3
t2 = tf.one_hot(indices, depth,on_value=5.0, off_value=0.0,axis=-1)
indices = [[0, 2], [1, -1]] depth = 3
t3 = tf.one_hot(indices, depth,on_value=1.0, off_value=0.0,axis=-1) # [ [[1. 0. 0.][0. 0. 1.]]
[[0. 1. 0.][0. 0. 0.]] ]
t = [1, 1, 2, 4, 4, 4, 7, 8, 8]
y, idx = tf.unique(t)
print(y) #t的所有唯一元素
print(idx) #y中每个值的索引
tf.math.ceil([-1.7,-1.5,-0.2,0.2,1.5,1.7,2.0]) #向上取整函数
tf.gather(params,indices,axis=0 ) 从params的axis维根据indices的参数值获取切片
- 运算
tf.diag(diagonal) 根据主对角线元素生成矩阵
tf.trace(x, name=None)求二维tensor对角值之和
tf.matrix_determinant(input, name=None)求方阵行列式
tf.matrix_inverse(input, adjoint=None,name=None)求逆矩阵
tf.matmul(a,b,transpose_a=False,transpose_b=False,a_is_sparse=False,b_is_sparse=False,name=None)矩阵相乘
tf.complex(real, imag, name=None) 将两实数转换为复数形式
tf.complex_abs(x, name=None) 计算复数的绝对值,即⻓度。
tf.conj(input, name=None) 计算共轭复数
tf.imag(input, name=None)
tf.real(input, name=None)
tf.eye(num_rows,num_columns=None)生成单位阵
tf.fill(dims,value,name=None) fill([2, 3], 9) ==> [[9, 9, 9][9, 9, 9]]
tf.ones(shape,dtype=tf.dtypes.float32,name=None)
- 数据生成
⽣成随机张量
tf.random_normal(shape, mean=0.0, stddev=1.0, dtype=tf.float32, seed=None)
从“服从指定正态分布的序列”中随机取出指定个数的值,shape: 输出张量的形状,mean: 正态分布的均值,stddev: 正态分布的标准差,dtype: 输出的类型,seed: 随机数种子,是一个整数,当设置之后,每次生成的随机数都一样
tf.truncated_normal(shape, mean, stddev)
产生截断正态分布随机数,取值范围为 [ mean - 2 * stddev, mean + 2 * stddev ]
tf.random_uniform(shape,minval=0, maxval=None, dtype=tf.float32, seed=None)
生成的值在 [minval, maxval) 范围内遵循均匀分布.
tf.random_shuffle() 随机地将张量沿其第一维度打乱
变量:
biases = tf.Variable(tf.zeros([200]),name=“var") 生成一组变量(没有初始化)
const = tf.constant(1.0,name="constant") 创建常量
名称作用域
在TensorFlow 应用程序中,可能会有数以千计的计算节点。如此多节点汇集在一起,难以分析,甚至无法用标准的图表工具来展示。为解决这个问题,一个有效方法就是,为Op/Tensor 划定名称范围。在TensorFlow 中,这个机制叫名称作用域(name scope)
tf.variable_scope() 管理变量命名空间,可以创建同名变量。在tf.variable_scope 中创建的变量,名称. name 中名称前面会加入命名空间的名称,并通过“/” 来分隔命名空间名和变量名。
tf.get_variable(name="foo/bar", shape=[1]) ,可以通过带命名空间名称的变量名来获取其命名空间下的变量。如果变量存在,则使用以前创建的变量,如果不存在,则新创建一个变量。不能创建同名变量。
Pytorch
概念:Pytorch是一个基于python的科学计算包,主要用途为,
- 作为Numpy的替代品,可以利用GPU的性能进行高效计算
- 作为高灵活性,速度快的深度学习平台
测试:
torch.cuda.is_available()
x = torch.rand(5,3) print(x)
print(x)
基本元素: 张量(Tensor)、变量(Variable)、神经网络模块(nn.Module)
- 张量(Tensor):张量是PyTorch中最基本的元素,相当于numpy.ndarray。Tensor是PyTorch中numpy.ndarray的替代品。
- 变量(Variable):搭建神经⽹络时,需要variable来构建计算图。
- Variable是对tensor的封装,是⼀个存放会变化的值(tensor)的物理位置。
- variable有3个属性:
- variable.data: variable中tensor的值
- variable.grad: variable中tensor的梯度;
- variable.gradfn: 指向Function对象,⽤于反向传播的梯度计算之⽤
nn.Module
神经⽹络模块nn.Module:神经⽹络的接⼝。定义⾃⼰的神经⽹络时,需继承 nn.Module类
- (1) Liner模块
torch.nn.Linear(in_features, out_features, bias=True)
⽹络中的全连接层,全连接层输⼊与输出都是⼆维张量,输⼊形状为[batch_size, size]。
in_features:指的是输入的二维张量的大小。
out_features:指的是输出的二维张量的大小,即输出的二维张量的形状为[batch_size,output_size],也代表该全连接层的神经元个数。
- (2) Conv2d模块
torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)
kernel_size:卷积核的⼤⼩,⽤(H,W)表示HxW的输出,H表示H*H⼤⼩的输出。
stride:卷积步幅,卷积核每次挪动间距
padding:填充操作,控制padding_mode的数⽬。默认为Zero-padding。
dilation:扩张操作,控制kernel点(卷积核点)的间距,默认为1。
group:控制分组卷积,默认不分组。 (对输入feature map进行分组,然后每组分别卷积。)
bias:是否添加偏置,如为真,则在输出中添加⼀个可学习的偏差,默认为True。
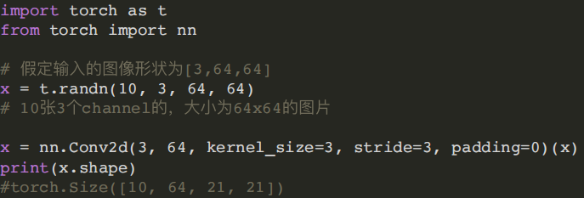
- Linear和Conv2d连接,Conv2d的输出为四维张量,转换为⼆维张量之后,才能作为全连接层的输⼊。
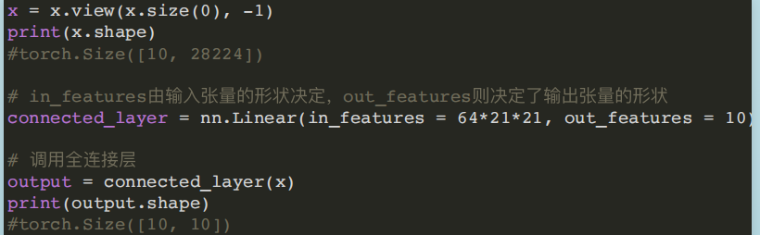
- (3)⼆维批量归⼀化模块
torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True)
num_features:特征数C
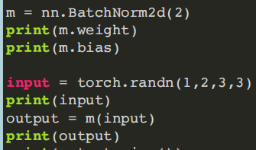
- (4)最⼤池化模块
torch.nn.MaxPool2d(kernel_size, stride=None, padding=0, dilation=1)
输⼊: (N,C,H_in,W_in)
输出: (N,C,H_out,W_out)
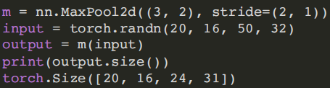
- (5)平均池化模块:
torch.nn.AvgPool2d(kernel_size, stride=None, padding=0, ceil_mode=False)
ceil_mode:如果为True,则在计算输出形状时使⽤ceil函数替代floor
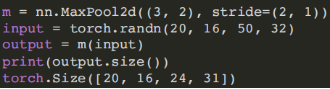
- (6)⾃适应平均池化模块:
torch.nn.AdaptiveAvgPool2d(output_size) output_size: 输出信号的尺⼨
Adaptive Pooling特殊性在于输出张量的⼤⼩是给定的output_size。对于任何输⼊⼤⼩的输⼊,可以将输出尺⼨指定为H*W,但是输⼊和输出特征的数⽬不会变化。
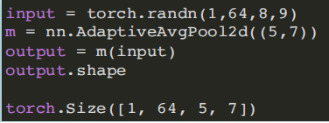
nn.function
- 位置:torch.nn.functional
例:torch.nn.functional.adaptive_avg_pool2d(input, output_size) torch.nn.ReLU(inplace=False)inplace:选择是否进⾏原位运算,即x = x+1- Sigmoid:
m = nn.Sigmoid()
input = torch.randn(2)
output = m(input)
input, output
(tensor([-0.8425, 0.7383]), tensor([0.3010, 0.6766]))
4.Tanh:
m = nn.Tanh()
input = torch.randn(2)
output = m(input)
input, output
(tensor([1.3372, 0.6170]), tensor([0.8710, 0.5490]))
RNN
函数:torch.nn.RNN(input_size, hidden_size, num_layers)
- hidden_size:隐含层神经元个数,也是输出的维度,因为rnn输出为各时间步上的隐藏状态;
- num_layers:隐含层的层数;
RNN的输出包含两部分:输出值Y(即output)和 最后⼀个时刻隐含层的输出 h n h_n hn
前向预测:
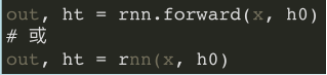
- x:[seq_len, batch, feature_len],是⼀次性将所有时刻特征输⼊的,不需要每次输⼊当前时刻的xt;
- h0是第⼀个初始时刻所有层的记忆单元的Tensor(理解成每⼀层中每个句⼦的隐藏输出);
例:输⼊⼀段中⽂,输出⼀段英⽂。每个中⽂字符⽤100维数据进⾏编码,每个隐含层的维度是20,有4个隐含层。所以input_size = 100,hidden_size = 20,num_layers = 4。设模型已经训练好了,现在有个1个⻓度为10的句⼦做输⼊,那seq_len = 10, batch_size = 1。
import torch
import torch.nn as nn
input_size = 100 # 输⼊数据编码的维度
hidden_size = 20 # 隐含层维度
num_layers = 4 # 隐含层层数
rnn = nn.RNN(input_size=input_size,hidden_size=hidden_size,num_layers=num_layers)
print("rnn:",rnn)
seq_len = 10 # 句⼦⻓度
batch_size = 1
x = torch.randn(seq_len,batch_size,input_size) # 输⼊数据x
h0 = torch.zeros(num_layers,batch_size,hidden_size) # 输⼊数据h0
out, h = rnn(x, h0) # 输出数据
print("out.shape:",out.shape)
print("h.shape:",h.shape)
- RNNCell模块:
(1)区别:nn.RNN是⼀次性将所有时刻特征输⼊⽹络的。nn.RNNCell将序列上的‘每个时刻的数据’分开来处理
(2)前向预测: h t = f o r w a r d ( x t , h t − 1 ) h_t = forward(x_t, h_{t-1}) ht=forward(xt,ht−1)
例如:如果要处理3个句⼦,每个句⼦10个单词,每个单词⽤100维的嵌⼊向量表示
nn.RNN传⼊的Tensor的shape是[10,3,100]
nn.RNNCell传⼊的Tensor的shape是[3,100],将此计算单元运⾏10次
- LSTM模块
- 函数:
torch.nn.LSTM(input_size, hidden_size, num_layers) - 输⼊及输出格式:
out, (h_t, c_t) = lstm(x, [h_t0, c_t0]) - LSTMCell模块:
h_t, c_t = lstmcell(x_t, [h_t-1, c_t-1])- xt:[batch, feature_len]表示t时刻的输⼊
- ht−1,ct−1:[batch, hidden_len],t−1时刻本层的隐藏单元和记忆单元)
- 函数:
nn.LSTM是⼀次性将所有时刻特征输⼊⽹络的。
nn.LSTMCell将序列上的‘每个时刻的数据’分开来处理
CNN
- 前馈型神经网络的学习主要采用误差修正法(如BP算法),计算过程比较慢,收敛速度也较慢;
- 而反馈型神经网络主要采用Hebb学习规则,计算收敛速度很快。
CNN使用部分连接层,三个思想为局部性、相同性、不变性
卷积层
- 第一层神经元只连接输入图像中位于他感知区域中的像素 专注图像的低级特征
- 第二层神经元仅连接到位于第一层中感知区域内的神经元 高级特征
过滤器(Filters、卷积核) 卷积操作 设定参数
1)滤波器的长宽高 HWC
2)步长(Stride)
3)边界填充

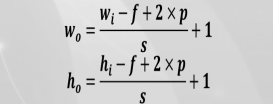
注:经过滤器处理后的图像称为特征图,特征图中所有神经元共享相同参数(权重、偏差顷)
基本结构(输入层+卷积层(提取特征)+池化层(压缩特征)+ 全连接层(非线性输出))
- 输⼊图像的表示:3D张量 [⾼度,宽度,通道];
- ⼩批量表示:4D张量 [⼩批量,⾼度,宽度,通道];
卷积层的权重表示:4D张量 [ fh,fw,fn,fn′]
- fh为当前层过滤器高度 ;fw为当前层过滤器宽度;fn为当前层过滤器数量 ;fn’为上一层特征图数量
卷积层的偏置项表示:1D张量 [fn]
计算:一个具有5×5过滤器的卷积层,输出尺寸为150×100的200个特征图,带有步幅1和SAME填充。
参数数量:若输入是150×100 RGB图像(三通道),则参数的数量:(5×5×3+1)*200=15,200
200个特征图每一个都包含150×100个神经元,每个都需要计算其5×5×3=75个输入的加权和,总共有75*150*100*200=2.25亿次浮点乘法。
若用32位浮点数表示特征图,卷积层输出将占200×150×100×32=96百万位(约11.4 MB)内存
关于padding
写代码时,要注意,padding有两个模式,分别是 ‘same’ 和 ‘valid’ ,
padding='same'表示进行填充,填充的值由算法内部根据卷积核大小计算,目的是让输出尺寸和输入相等;
padding='valid'表示不进行填充,即是 padding=0,只使用有效的窗口位置,这是默认的选项。
- 填充的值= (b - 1) / 2
填充的值,b的值就是卷积核的尺寸,这里就是为什么卷积核尺寸通常选择奇数的原因
举例子:
问题1. 一个尺寸 55 的特征图,经过 33 的卷积层,步幅(stride)=1,想要输出尺寸和输入尺寸相等,填充(padding)的值应该等于多少?
答:填充的值=(3 - 1)/2 = 1,即每一边填充1层
问题2. 一个尺寸 224224 的特征图,经过 77 的卷积层,步幅(stride)=2,想要输出尺寸和输入尺寸相等,填充(padding)的值应该等于多少?
答:填充的值=(7 - 1)/2 = 3,即每一边填充3层
- padding='same’目的是让输出尺寸和输入尺寸相等,但前提是步幅=1,步幅若不是1,那么输出尺寸跟输入尺寸肯定是不一样。
对于 padding 的 same 和 valid 模式两种直白的理解就是要么不填充,要么填充就让输出尺寸和输入尺寸相等
padding 的值不会乱取,就两种情况,要么padding=0 要么padding=(b - 1)/2。
池化层:
1)⽬标:对输⼊图像进⾏⼆次采样(即缩⼩),以减少计算量、内存占⽤和参数数量(减少过拟合⻛险)
2)特点:池化层中的每个神经元都和前⼀层神经元的输出相连,位于⼀个⼩的矩形感受区内。但池化神经元没有权重,它⽤聚合函数(如max_pool()或avg_pool())聚合输⼊。
3)作用:特征降维,避免过拟合;空间不变性;减少参数,降低训练难度
4)代码实现⼀个2x2内核的池化层(keras实现)
keras.layers.MaxPool2D( pool_size=(2,2), strides=None, #默认值和pool_size相等
padding='valid', data_format=None)
keras.layers.AvgPool2D(pool_size=(2,2),strides= None, # 默认值和pool_size相等
padding='valid', data_format=None)
keras.layers.GlobalAveragePooling2D(data_format=None)
- 设计一个对MNIST处理的CNN网络,结构和参数如下,每次MaxPooling后添加系数为0.25的Dropout.
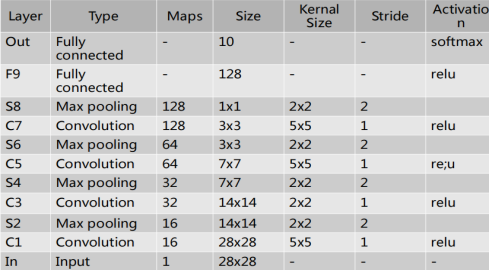
import os
import tensorflow as tf
from tensorflow.keras.datasets import mnist
from tensorflow.keras.utils import to_categorical
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Dropout, Flatten, Conv2D,
import numpy as np
(X_tarin, y_train), (X_test, y_test) = mnist.load_data()
X_train4D = X_tarin.reshape(X_tarin.shape[0], 28, 28, 1).astype('float32')
X_test4D = X_test.reshape(X_test.shape[0], 28, 28, 1).astype('float32')
# 归⼀化
X_train4D_Normalize = X_train4D / 255
X_test4D_Normalize = X_test4D / 255
# 标签onehot编码
y_trainOnehot = to_categorical(y_train)
y_testOnehot = to_categorical(y_test)
# 建⽴模型
model = Sequential()
model.add(Conv2D(filters=16,kernel_size=(5, 5),padding='SAME', input_shape=(28, 28, 1),activation='relu'))
model.add(MaxPool2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
# ⼆层卷积
model.add(Conv2D(filters=32,kernel_size=(5, 5), padding='SAME', activation='relu'))
model.add(MaxPool2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
#三、四层卷积
model.add(Conv2D(filters=64, kernel_size=(5, 5), padding='same', activation='relu'))
model.add(MaxPool2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Conv2D(filters=128, kernel_size=(5, 5), padding='same', activation='relu'))
model.add(MaxPool2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
# 全连接层
model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.25))
model.add(Dense(10, activation='softmax'))
model.summary()
# 编译模型
model.compile(loss='categorical_crossentropy',optimizer='adam',metrics=['accuracy'])
#训练模型
train_history = model.fit(x=X_train4D_Normalize,y=y_trainOnehot,validation_split=0.2,batch_size=300,
epochs=10,verbose=2)
#评估模型
model.evaluate(X_test4D_Normalize, y_testOnehot)[1]
#预测
prediction = model.predict_classes(X_test4D_Normalize)
RNN
概念:⼀类⽤于处理序列数据的神经⽹络,⼀个序列当前的输出与前⾯的输出有关。具体的表现形式为:⽹络会对前⾯的信息进⾏记忆并应⽤于当前输出的计算中,即隐藏层之间的节点是有连接的,并且隐藏层的输⼊不仅包括输⼊层的输出还包括上⼀时刻隐藏层的输出。
结构:
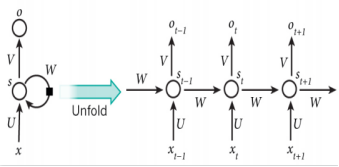
参数3组权重:
- U(输⼊x和节点间的计算)
- W(节点随时间转换计算)
- V:(节点x和输出节点间计算)
- St为时刻t隐层的状态 s t = f ( U x t + W s t − 1 ) s_t = f(U_{x_t} + W_{s_t−1}) st=f(Uxt+Wst−1)
激励函数 :⼀般为tanh或ReLU
o
t
o_t
ot为时刻t的输出。
o
t
=
s
o
f
t
m
a
x
(
V
s
t
)
o_t = softmax(V_{s_t})
ot=softmax(Vst)
分类:
- 按输⼊和输出序列的结构:One to One、One to Many(向量到序列)、Many to One(序列到向量)、Many to Many 、Encoder-Decoder模型(Seq2Seq模型)
- 按内部结构:传统RNN、LSTM、Bi-LSTM、GRU、Bi-GRU
简单RNN缺点:在预测⻓序列上表现不佳,⾯临不稳定梯度问题,易发生梯度消失或爆炸;且当 RNN 处理⻓序列时,会逐渐忘掉序列的第⼀个输⼊
- 简易RNN
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.SimpleRNN(1, input_shape=[None, 1]) ])
optimizer = keras.optimizers.Adam(learning_rate=0.005)
model.compile(loss="mse", optimizer=optimizer)
history = model.fit(X_train, y_train, epochs=20,validation_data=(X_valid, y_valid))
model.evaluate(X_valid, y_valid)
y_pred = model.predict(X_valid)
- 深度RNN
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.SimpleRNN(20, return_sequences=True,input_shape=[None, 1]),
keras.layers.SimpleRNN(20, return_sequences=True),
keras.layers.SimpleRNN(1)
])
model.compile(loss="mse", optimizer="adam")
history = model.fit(X_train, y_train, epochs=20,validation_data=(X_valid, y_valid))
model.evaluate(X_valid, y_valid)
y_pred = model.predict(X_valid)
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None, 1])
keras.layers.BatchNormalization(),
keras.layers.SimpleRNN(20, return_sequences=True),
keras.layers.BatchNormalization(), 批量归一化
keras.layers.TimeDistributed(keras.layers.Dense(10)) 时间步
每⼀步都预测10个值,即在时刻0会预测1到10,时刻1预测2到11.
])
model.summary()
model.compile(loss="mse", optimizer="adam", metrics=[last_time_step_mse])
history = model.fit(X_train, Y_train, epochs=20, validation_data=(X_valid, Y_valid))
model.evaluate(X_valid, Y_valid)
LSTM
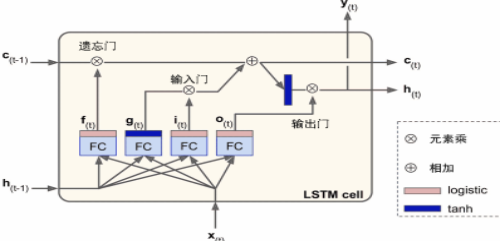
- LSTM 单元的状态:h[t](短期记忆状态),c[t](⻓期记忆状态)
c[t−1]先经遗忘⻔丢弃⼀些记忆;后经添加操作增加⼀些记忆(从输⼊⻔中选
择⼀些),最后不经转换直接输出。添加操作之后,⻓时状态复制后经tanh 激活函数,后结果被输出⻔过滤,得到短时状态h[t]。h[t]即为这⼀时间步的单元输出y[t]。
短期记忆状态
h
[
t
−
1
]
h[t−1]
h[t−1]和输⼊向量
x
[
t
]
x[t]
x[t]经4个不同的全连接层:
g
[
t
]
g[t]
g[t]层为主要层(将最重要的部分保存在⻓期状态中,tanh为激活函数),其它三个全连接层(FC)是⻔控制器(Logistic作为激活函数)
权重计算
W
x
i
,
W
x
f
,
W
x
o
,
W
x
g
W_{xi},W_{xf} ,W_{xo},W_{xg}
Wxi,Wxf,Wxo,Wxg是四个全连接层连接输⼊向量x(t)的权重;
W
h
i
,
W
h
f
,
W
h
o
,
W
h
g
W_{hi},W_{hf} ,W_{ho},W_{hg}
Whi,Whf,Who,Whg是四个全连接层连接h(t−1)的权重;
b
i
,
b
f
,
b
o
,
b
g
b_i,b_f ,b_o,b_g
bi,bf,bo,bg是全连接层的四个偏置项。
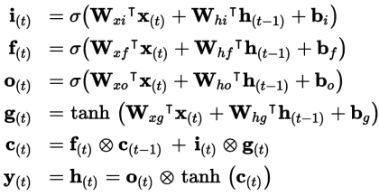
W
x
i
,
W
x
f
,
W
x
o
,
W
x
g
W_{xi},W_{xf} ,W_{xo},W_{xg}
Wxi,Wxf,Wxo,Wxg 权重数量:
输入参数数量×隐层参数数量+隐层参数数量 ×隐层参数数量
偏置数量:隐层参数数量
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.LSTM(20, return_sequences=True, input_shape=[None, 1]),
keras.layers.LSTM(20, return_sequences=True),
keras.layers.TimeDistributed(keras.layers.Dense(10))
])
model.summary()
model.compile(loss="mse", optimizer="adam", metrics=[last_time_step_mse])
history = model.fit(X_train, Y_train, epochs=20, validation_data=(X_valid, Y_valid))
model.evaluate(X_valid, Y_valid)
GRU
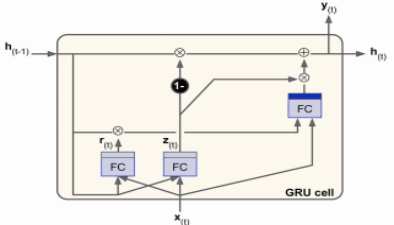
⻓时状态和短时状态合并为⼀个向量h(t)。⽤⼀个⻔控制器z(t)(重置门)控制遗忘⻔和输⼊⻔
- (若⻔控制器输出1,则遗忘⻔打开(= 1),输⼊⻔关闭(1 - 1 = 0)。
- 若输出0,则做相反操作)取消输出⻔,每个时间步输出全态向量。
增加⼀个控制门r(t)(更新门)来控制前⼀状态的哪些部分呈现给主层g(t)
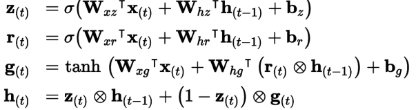
- 注:尽管它们相⽐于简单RNN可处理更⻓的序列了,还是有⼀定程度的短时记忆。
应对⽅法之⼀是将输⼊序列缩短,例如使⽤ 1D 卷积层。1D 卷积层在序列上滑动⼏个核,每个核可以产⽣⼀个 1D 特征映射。 每个核能学到⼀个⾮常短序列模式(不会超过核的⼤⼩)
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.GRU(20, return_sequences=True, input_shape=[None, 1]),
keras.layers.GRU(20, return_sequences=True),
keras.layers.TimeDistributed(keras.layers.Dense(10))
])
model.summary()
model.compile(loss="mse", optimizer="adam", metrics=[last_time_step_mse])
history = model.fit(X_train, Y_train, epochs=20, validation_data=(X_valid, Y_valid))
- 实现RNN对数据集MNIST的分类任务
import torch
import torch.nn as nn
import torchvision.datasets as ds
import torchvision.transforms as transforms
from torch.autograd import Variable
sequence_length = 28 , input_size = 28 , hidden_size = 128
num_layers = 2, num_classes = 10 , batch_size = 100 , num_epochs = 2
learning_rate = 0.003
#加载MNIST数据集
train_dataset = ds.MNIST(root='.data',train=True,transform=transforms.ToTensor(),download=True)
test_dataset = ds.MNIST(root='.data',train=False,transform=transforms.ToTensor())
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,batch_size=batch_size,shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset,batch_size=batch_size,shuffle=False)
#定义多对⼀双向RNN模型
class BiRNN(nn.Module):
def __init__(self, input_size, hidden_size, num_layers, num_classes):
super(BiRNN, self).__init__()
self.hidden_size = hidden_size
self.num_layers = num_layers
self.lstm = nn.LSTM(input_size, hidden_size, num_layers,
batch_first=True, bidirectional=True)
self.fc = nn.Linear(hidden_size * 2, num_classes)
def forward(self, x):
h0 = Variable(torch.zeros(self.num_layers * 2, x.size(0),self.hidden_size)) # 设置初始状态
c0 = Variable(torch.zeros(self.num_layers * 2, x.size(0),self.hidden_size))
out, _ = self.lstm(x, (h0, c0)) #前向传播
out = self.fc(out[:, -1, :]) # 上一时间步隐藏状态输出
return out
#定义模型
rnn = BiRNN(input_size, hidden_size, num_layers, num_classes)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(rnn.parameters(), lr=learning_rate)
#训练模型
for epoch in range(num_epochs):
for i, (images, labels) in enumerate(train_loader):
images = Variable(images.view(-1, sequence_length, input_size))
labels = Variable(labels)
optimizer.zero_grad()#前向+后向+优化器
outputs = rnn(images)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
if (i + 1) % 100 == 0:
print('Epoch [%d/%d], Step [%d/%d], Loss: %.4f'% (epoch+1,num_epochs,i + 1, len(train_dataset)
// batch_size, loss.item()))
# 测试模型
correct = 0
total = 0
for images, labels in test_loader:
images = Variable(images.view(-1, sequence_length, input_size))
outputs = rnn(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted.cpu() == labels).sum()
print('Test Accuracy of the model on test images: %d %%' % (100 * correct / total))
AE
- 特征
自动编码器通常具有比输入数据低得多的维度,使其可以实现降维目的。
自动编码器还可以应⽤于降噪场合。
自动编码器还可以作为强⼤的特征检测器,它们可以⽤于⽆监督的深度神经⽹络预训练。
⼀些自动编码器是生成式模型,能够随机生成与训练数据⾮常相似的新数据。 - 自动编码器由两部分组成:
识别⽹络: 将输⼊转换为潜在表征的编码器
⽣成⽹络: 将潜在表征转换为输出的解码器 - 数据的潜在空间表示包含表示原始数据点所需的所有重要信息。该表示必须表示原始数据的特征。换句话说,该模型学习数据特征并简化其表示,从⽽使其更易于分析。
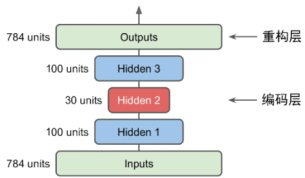
- 输出层中的神经元数量必须等于输⼊数量。⾃动编码器试图重构输⼊,所以输出通常被称为重建,并且损失函数包含重建损失,当重建与输⼊不同时,重建损失会对模型进⾏惩罚。
X_train = np.random.rand(100,3)
encoder = Sequential([Dense(2, input_shape=[3])])
decoder = Sequential([Dense(3)])
autoencoder = Sequential([encoder, decoder])
autoencoder.compile(loss="mse", optimizer=SGD(lr=0.1))
history = autoencoder.fit(X_train, X_train, epochs=20)
codings = encoder.predict(X_train)
自动编码器被迫学习输⼊数据中最重要的特征,并且要删除不重要的特征。(借助PCA)如果⾃动编码器仅使⽤线性激活并且损失函数是均⽅误差(MSE),最终其实是做了主成分分析(PCA)

深度自动编码器
⾃动编码器可以有多个隐藏层,称为深度⾃动编码器。
添加更多层有助于⾃动编码器学习更复杂的编码。 但不要让⾃动编码器功能太强⼤。
如果⼀个编码器太强⼤,就会导致过拟合问题, 这样的⾃动编码器将完美地重构训练数据,但它不会在过程中学习到任何有⽤的数据表征,并且它不可能很好地泛化到新的实例。
import utils.mnist_reader
X_train, y_train = utils.mnist_reader.load_mnist('./data/', kind='train')
X_valid, y_valid = utils.mnist_reader.load_mnist('./data/', kind='t10k')
X_train = X_train.reshape(X_train.shape[0],28,28).astype('float32')
X_valid = X_valid.reshape(X_valid.shape[0],28,28).astype('float32')
stacked_encoder = Sequential([
Flatten(input_shape=[28, 28]),
Dense(100, activation="selu"),
Dense(30, activation="selu"),
])
stacked_decoder = Sequential([
Dense(100, activation="selu", input_shape=[30]),
Dense(28 * 28, activation="sigmoid"),
Reshape([28, 28])
])
stacked_ae = Sequential([stacked_encoder, stacked_decoder])
stacked_ae.compile( loss="binary_crossentropy", optimizer=SGD(lr=1.5))
history = stacked_ae.fit(X_train,X_train,epochs=10,validation_data=[X_valid])
卷积自动编码
卷积⾃动编码器通常会降低输⼊的空间维度(即,⾼和宽),同时增加深度(即,特征映射的数量)。⽽解码器的⼯作相反,即放⼤图⽚,压缩深度。可以通过转置卷积层实现。也可以将上采样层和卷积层合并。
conv_encoder = Sequential([
Reshape([28, 28, 1], input_shape=[28, 28]),
Conv2D(16, kernel_size=3, padding="same", activation="selu"),
MaxPool2D(pool_size=2),
Conv2D(32, kernel_size=3, padding="same", activation="selu"),
MaxPool2D(pool_size=2),
Conv2D(64, kernel_size=3, padding="same", activation="selu"),
MaxPool2D(pool_size=2)
])
conv_decoder = Sequential([
Conv2DTranspose(32, kernel_size=3, strides=2, padding="valid",
activation="selu", input_shape=[3, 3, 64]),
Conv2DTranspose(16, kernel_size=3, strides=2, padding="same",
activation="selu"),
Conv2DTranspose(1, kernel_size=3, strides=2, padding="same",
activation="sigmoid"),
Reshape([28, 28])
])
conv_ae = Sequential([conv_encoder, conv_decoder])
-
反卷积:
⼀种⽤于扩⼤图像的尺⼨的⽅法,称为逆卷积或反卷积。
例如:输⼊特征图:3 ∗ 3 输⼊卷积核:kernel=3 ∗ 3, stride=2,padding=1
输出特征图:3 * 3 - 3 + 2 * 1 +1 = 5 -
循环自动编码器
循环⾃动编码器中的编码器是⼀个序列到向量的 RNN,⽽解码器是向量到序列的 RNN。
recurrent_encoder = Sequential([
LSTM(100, return_sequences=True, input_shape=[None, 28]),
LSTM(30)
])
recurrent_decoder = Sequential([
RepeatVector(28, input_shape=[30]), 将输⼊重复28次
LSTM(100, return_sequences=True),
TimeDistributed(Dense(28, activation="sigmoid"))将Dense层应⽤于输⼊的每个时间⽚(对输入的每个向量进行一次Dense操作)。
])
recurrent_ae = Sequential([recurrent_encoder, recurrent_decoder])
- VAE(变分自编码)
损失函数:
- 重建损失:推动⾃动编码器重现其输⼊。
- 潜在损失:推动⾃动编码器使编码看起来像是从简单的⾼斯分布中采样;
使⽤⽬标分布(⾼斯分布)与编码实际分布之间的 KL散度
变分⾃动编码器不是直接为给定的输⼊⽣成编码;编码器产⽣平均编码μ和标准差σ, 然后从平均值μ和标准差σ的⾼斯分布随机采样实现编码。之后,解码器正常解码采样的编码。
- 通过随机采样,可以将之前离散的潜在属性空间变为连续、平滑的潜在空间。
RL
Agent:智能体,也就是机器人,你的代码。
Environment:环境,也就是游戏本身,openai gym提供了多款游戏,也就是提供了多个游戏环境。
Action:行动,比如玩超级玛丽,向上向下等动作。
State:状态,每次智能体做出行动,环境会相应地做出反应,返回一个状态和奖励。
Reward:奖励:根据游戏规则的得分。智能体不知道怎么才能得分,它通过不断地尝试来理解游戏规则,比如它在这个状态做出向上的动作,得分,那么下一次它处于这个环境状态,就倾向于做出向上的动作。
在强化学习中,智能体(Agent)在环境(Environment)中观察(Observation)状态(State)并且做出决策(Action),随后它会得到奖励(Reward)。
- 智能体的目标是去学习如何行动能最大化期望奖励。
gym的核心接口是统一的环境Env,Env包含下面几个核心方法:
1、reset(self):重置环境的状态,返回观察值 observation 。
2、step(self,action):推进一个时间步长,返回[observation,reward,done,info]
3、render(self,mode='human', close=False): 重绘环境的一帧。默认模式一般比较友好,如弹出一个窗口。
4、info(dict):用于调试的诊断信息。
5、observation(object):返回一个特定环境的对象,描述对环境的观察。比如,来自相机的像素数 据,机器人的关节角度和关节速度,或棋盘游戏中 的棋盘状态。
6、reward(float):返回之前动作收获的总的奖 励值。
7、done(boolean):返回是否应该重新设置 (reset)环境。大多数游戏任务分为多个环节 (episode),当done=true的时候,表示这个环节结束了。
对于 CartPole 环境,每个观测是包含四个浮点的 1D Numpy 向量:
1.小车的水平位置(0 为中心)
2.小车的速度
3.杆的角度(垂直)
4.杆的角速度
CartPole-v0示例
env = gym.make('CartPole-v0') # 初始化环境
for i_episode in range(20): # 外层循环
obs = env.reset() 返回观察值
for t in range(100): # 内层循环
env.render() 重绘环境的一帧。
action = env.action_space.sample() 随机选取动作
obs, re, done, info = env.step(action)
print(obs)
if done:
print("done == True : %d" % (t+1))
break
env.close()
深度强化学习
策略搜索
在强化学习中,被智能体(Agent)使用去改变它行为的算法叫做策略(Policy)。例如,策略可以是一个把观测(Observations)当输入,行为(Actions)当做输出的神经网络。
搜寻策略方法:
1)随机策略:这个策略可以是你能想到的任何算法;
2)尝试策略:可以通过尝试来搜索,即通过大量实验来选择参数的最佳组合;
3)遗传算法:通过遗传算法来搜索最佳参数
4)策略梯度(PG):使用优化技术,通过评估奖励关于策略参数的梯度,然后通过跟随梯度向更高的奖励(梯度上升)调整这些参数;
5)神经网络策略:神经网络将把观察作为输入,输出要执行的动作。它将估计每个动作的概率,然后我们将根据估计的概率随机地选择一个动作。
Q:为什么根据神经网络给出的概率来选择随机的动作,而不是选择最高分数的动作?
A:这种方法使智能体在探索新的行为和选择可行的行动之间找到平衡。
评价行为:信用分配问题
在强化学习中,智能体获得的指导的唯一途径是通过奖励,奖励通常是稀疏的和有延迟的。
信用分配问题:当智能体得到奖励时,如何知道哪些行为应该被信任(或责备)。
解决策略:是基于这个动作后得分的总和来评估这个动作,通常在每个步骤中应用衰减率r。如果衰减率接近0,那么与即时奖励相比,未来的奖励不会有多大意义。相反,如果衰减率接近1,那么对未来的奖励几乎等于即时回报。
如果一个智能体决定连续三次向右,在第一步之后得到 +10 奖励,第二步后得到 0,第三步之后得到 -50,衰减率r=0.8,那么第一个动作将得到 10 + r × 0 + r 2 × ( − 50 ) = 10 + 0.8 × 0 + 0. 8 2 × ( − 50 ) = − 22 10+ r ×0+ r^2 ×(−50) = 10+0.8×0+0.8^2 ×(−50)=−22 10+r×0+r2×(−50)=10+0.8×0+0.82×(−50)=−22的分数。
Q-Learning
- 马尔科夫链
包含N个状态,从某个状态到其它状态的转移概率(Transition Probability)是确定的,且不取决于过去的状态(系统没有记忆)。将来的状态分布只取决于现在,跟过去无关。所有状态之间的转移概率关系可以用一个矩阵表示,称为转移矩阵(Transition Matrix)。 - 马尔可夫决策过程(MDP):
1)在每个步骤中,agent 可以选择几种可能的动作中的一个,并且转移概率取决于所选择的动作。一些状态转换会返回一些奖励(正面或负面),而agent的目标是找到一种能够随着时间的推移最大化回报的策略。
2)一种估算任何状态s的最佳状态值的方法,记为V*(s):
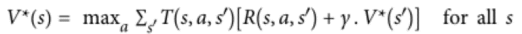
- T(s,a,s’)是agent 选择了动作a时,从状态s到状态s’的转换概率。
- R(s,a,s’)是agent选择了动作a时,从状态s到状态s’时获得的奖励。γ是折扣率。
Q值迭代算法:
动态规划的一个例子,它将一个复杂的问题分解为易处理的子问题,并且可以通过迭代解决。
原理:将状态-动作值 (s,a) 称为Q值,记为Q(s,a),它将返回在该状态下执行该动作的未来奖励期望。状态-动作(s,a)的最佳Q值,记为Q*(s,a)。
- 工作原理:首先将所有Q值估算值初始化为零,然后使用Q值迭代算法更新它们。
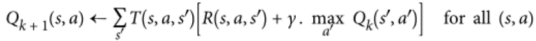
Q-Learning算法是Q值迭代算法适应转移概率和奖励未知的情况。
对于每个状态 - 动作对(s,a),算法跟踪agent 在离开状态s时采取动作a的奖励的运行平均值,以及预期稍后获得的奖励。由于目标策略将采取最优行动,因此我们对下一个状态采取最大Q值估计。
估值Q-Learning
Q-Learning的主要问题是它不能很好地扩展到具有许多状态和动作的大型、中型MDP问题。找到一个使用参数数量可管理的函数来近似Q值,称为估值Q-Learning
- 用于估计Q值的DNN称为深度Q网络(DQN)。使用DQN进行近似Q学习称为深度Q学习(DQL)。
Q-learning 示例
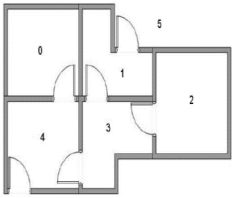
用一个简单的例子介绍Q-Learning算法的执行过程。在一幢建筑里有6个房间,房间用编号0-5表示,房间之间通过门相连。房间5是建筑外围空间,可以看作是一个大的房间。首先将Agent置于建筑中任意一个房间,其1目标是从那个房间开始走到房间5。
-
初始化:初始化Q,R,γ
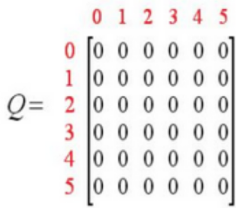
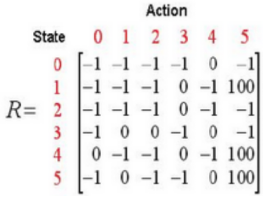
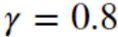
-
Q-Learning算法
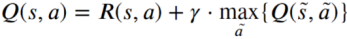
Step 1 给定参数 和R矩阵,Q=0.
Step 2 循环执行Step3,4
Step 3 随机选择一个初始状态s
Step 4 循环执行:
1.判断s是否是目标状态,如否则执行下列步骤,如是则结束Step 4.
2.在当前状态s的所有可能行动中选取一个动作a
3.利用选定的动作a,得到下一个状态s~
4.利用公式计算Q(s,a)
5.令s=s~
-
执行过程
循环1 令初始状态为1。 状态不为5,则在R矩阵中选择状态1的可能动作:3或5。 选择状态5,得到下一个状态为5。 利用公式计算Q(1,5) Q矩阵更新为: 当前状态为5,所以下次循环判断后即可结束
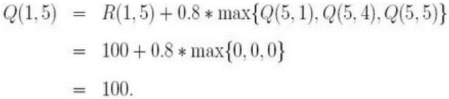

循环2
回到Step 3, 重新选择一个初始状态。
选择初始状态为3.
找出状态3的可能动作:1,2,4
选择状态1,对应2个可能的动作:3或5
利用公式计算Q(3,1)
Q矩阵更新为:
现在的当前状态变成了状态1,因为状态1不是目标状态,因此从状态1 的可能动作选择一个:3或5。
选择状态5,其动作有3个可能:1,4或5;
利用公式计算Q(1,5)
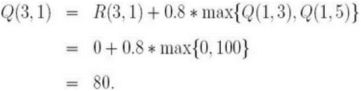
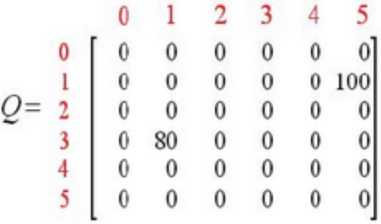


继续循环,继续执行多次后,将得到矩阵Q:
一旦Q接近收敛状态,就可以指导Agent进行最佳路径选择。
如,假定Agent从状态2出发,可到到下列路径:
1. Q矩阵中,状态2的最大元素值为320,选择状态3;
2. 状态3的最大元素值为400, 状态为1或4,选择状态4;
3. 状态4的最大元素值为500,即状态5,到达目标。
因此最佳路径为:2-3-4-5






 QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) Allegro16.6差分等长设置及走线总结
Allegro16.6差分等长设置及走线总结