您现在的位置是:首页 >技术教程 >【八大排序(一)】排序还只会用冒泡?进来给我学!网站首页技术教程
【八大排序(一)】排序还只会用冒泡?进来给我学!
?博主CSDN主页:杭电码农-NEO?
⏩专栏分类:八大排序专栏⏪
?代码仓库:NEO的学习日记?
?关注我?带你学习排序知识
??

插入,希尔排序
1. 前言?
博主前段时间接到了专业课老师的任务:
让我设计个排序算法用来给学生成绩排名.
我心里一惊!
这不是为难我这个只会冒泡的大学生嘛

于是我删掉了王者荣耀,删掉了吃鸡
我奋不顾身,我披星戴月的肝八大排序
终于!我现在学成归来
下面就给大家分享八大排序中的前两个:
- 插入排序
- 选择排序
2. 插入排序?
2.1 基本思路?
基本思想:
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
玩斗地主抓牌实际上就是一种插入排序:

2.2 画图理解?
单趟插入:
比如我们先定义一个有序数组:
int a[100]={2,4,5,10};
我们再把数据3插入到这个数组中:
插入排序
2.3 代码实现?
在我们实际生活中
最常见的就是把一个无序数组变成有序
所以还不能是单纯的插入到有序数组中
这里我们将一个无序数组变为有序
直接在原数组中操作
这里我们定义一个无序数组:
int a[9]={2,9,5,7,4,1,3,8,6}
要想直接在原数组中操作,相当于要进行元素个数这么多次单趟插入,我们定义两个变量,end和x,一个指向第一个元素,一个指向第二个元素,end<x就不移动,end>x就开始往后走
画图:
原数组插入
// 插入排序
void InsertSort(int* a, int n)
{
assert(a);
for (int i = 0; i < n - 1; i++)//将一个数组中所有元素升序
{ //,这里必须是n-1,不然后面数组会越界
int end=i;
int x=a[end+1];//x始终指向end下一个位置的值
while (end >= 0)//每趟插入最多挪动end-1个数据
{
if (a[end] > x)//x前一个数大于x,就将数据往后移一格
{
a[end + 1] = a[end];//这里数组的值会往后覆盖
//但是没关系,我们已经将a[end+1]的值保存在x当中了
end--;
}
else
{
break;//跳出里面的while循环
}
}
a[end + 1] = x;
}
}
3. 选择排序?
3.1 基本思想?
基本思想:
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完
不知道你们有没有经历过这种痛:
小学排队的时候老师对我说:
你,最矮!到最前面来排着.
当然大家可能之前接触过选择排序
但是我分享的选择排序是做了优化的
以前我们是每一趟选一个最大或最小
优化后:一趟选两个,最大的和最小的
分别放在数组的左右端
3.2 画图理解?
我们先定义一个1~9的无序数组:
int a[9]={6,2,5,3,9,4,8,5,1,7}
这里的视频理解中,一趟只选出了一个
我们只要理解这个优化的思路就好了
选择排序
3.3 代码实现?
因为选择排序会用到交换
所以我们直接写一个交换函数
//交换函数
void swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
然后下面是我们的代码版本一:
void SelectSort(int* a, int n)
{
int begain = 0;
int end = n - 1;
while (begain < end)
{
int maxi = begain;//初始化最值
int mini = begain;
for (int i = begain; i <= end; i++)
{
if (a[i] < a[mini])
{
mini = i;//记录下标,否则会有数据被覆盖的问题
}
if (a[i] > a[maxi])
{
maxi = i;
}
}
swap(&a[begain], &a[mini]);//将最大最小值交换
swap(&a[end], &a[maxi]);
begain++;//数组范围往中间缩小
end--;
}
}
3.4 代码优化?
但是这个代码会出现一个问题:当数组中的最大值位于数组的第一个位置时,我们把begin和mini交换后,maxi指向的位置还是第一个元素,也就是最小值mini.再将maxi与end交换,就把最小值换到最后了!我们画图理解一下:

修改后的版本二
// 选择排序
void SelectSort(int* a, int n)
{
int begain = 0;
int end = n - 1;
while (begain < end)
{
int maxi = begain;
int mini = begain;
for (int i = begain; i <=end; i++)
{
if (a[i] < a[mini])
{
mini = i;//记录下标,否则会有数据被覆盖的问题
}
if (a[i] > a[maxi])
{
maxi = i;
}
}
swap(&a[begain], &a[mini]);
if (maxi == begain)//当最大值为begain时,交换最小值和开头元素后,maxi指向的值不再是最大值了.
{
maxi = mini;
}
swap(&a[end], &a[maxi]);
begain++;
end--;
}
}
4. 算法效率分析?
- 插入排序时间复杂度分析
- 最优情况:待排序的数组是有序的.
只需当前数跟后一个数比较一下
一共需要比较N- 1次
时间复杂度为 : O ( N )
- 最坏情况:待排序数组是逆序的
总次数记为:1+2+3+…+N-1
1代表第二个元素要移动一次.
2代表第三个元素要移动两次…
总共要挪动:(1+N-1)*(N-1)/2次
时间复杂度为:O ( N )
- 选择排序时间复杂度分析
选择排序不管数组有序还是无序
它都需要一遍一遍的遍历数组
即使我们这里做了一些优化
它还是要走2/N次,再乘以次数N
时间复杂度都是: O(N^2^)
5. 总结与网站分享?
我们的八大排序中,插入排序选择和冒泡
可以分为一类,可以横向对比
经过我们刚才的分析可以得出一个结论:
插入排序 > 冒泡排序 > 选择排序
好家伙
合着冒泡还不是最菜的是吧(狗头保命)

这里给大家分享两个动图网站
里面的动图可以帮助我们理解
算法和数据结构的问题.
分别是:
- https://visualgo.net/en 点击即可访问
包括各大排序,链表,二叉树,哈希表等等
我们可以在左上角将英文转换成中文
- https://www.cs.usfca.edu/~galles/visualization/about.html
点击即可访问
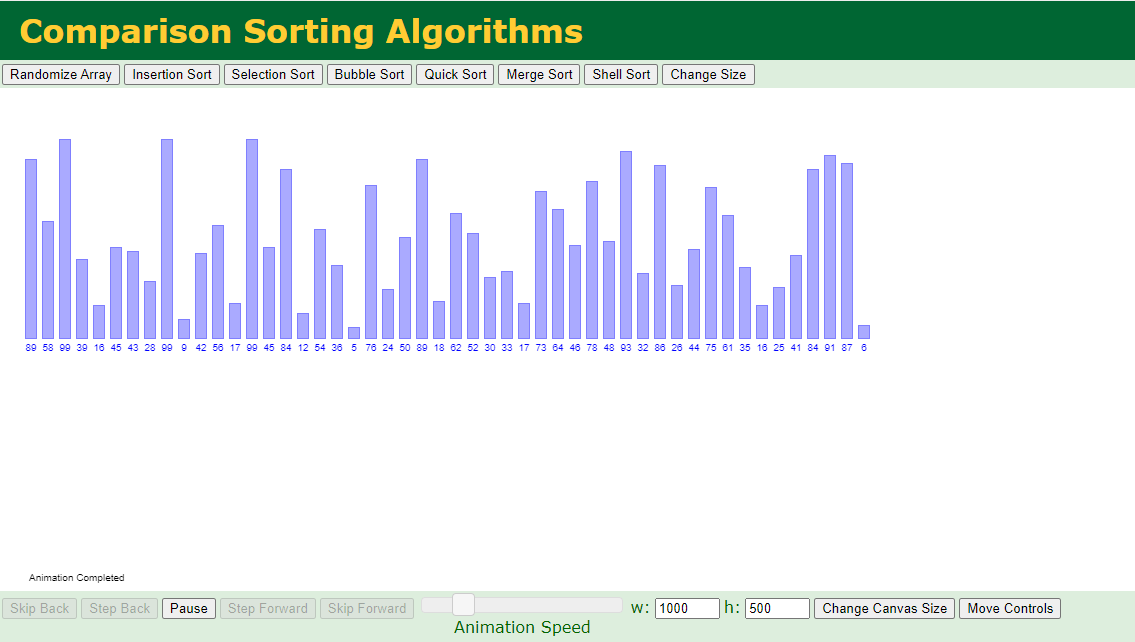
这个网站大家可以自己探索一下
小编也是最近才发现这个网站的






 QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) Allegro16.6差分等长设置及走线总结
Allegro16.6差分等长设置及走线总结