? ? 博客:小怡同学
? ? 个人简介:编程小萌新
? ? 如果博客对大家有用的话，请点赞关注再收藏 ?

堆的概念和结构

如果有一个关键码的集合K = { ， ， ，…， }，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足： <= 且 <= ( >= 且 >= ) i = 0，1，2…，则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。
//堆中某个节点的值总是不大于或不小于其父节点的值；
//堆总是一棵完全二叉树

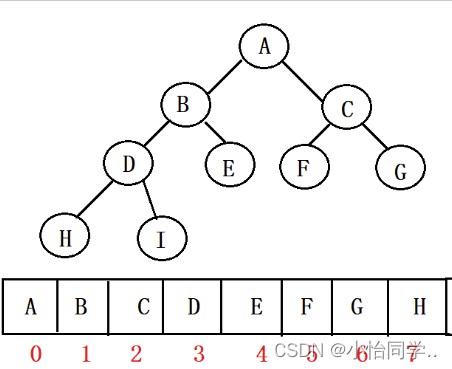
堆的实现

建堆的时间复杂度及堆排序的稳定性

向上调整建堆时间复杂度O( N*logN)
向下调整建堆时间复杂度O(N)
稳定性：不稳定

堆的向上调整

使用场景：建堆，堆的插入

void AdjustUp(int* a, int child)
{
	int parent = (child - 1) / 2;
	while ( child > 0 )
	{
		if (a[parent] < a[child])
		{
			swap(&a[parent], &a[child]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

堆的向下调整

使用场景：建堆，堆的删除，堆的排序

void AdjustDown(int* a,int parent,int n)
{
	for(int child = parent * 2 + 1; child <n; child=child*2+1)
	
	{
		if (child + 1 < n && a[child] <  a[child + 1])
		{
			child++;
		}
		if (a[child] > a[parent])
		{
			swap(&a[child], &a[parent]);
			parent = child;
		}
		else
		{
			break;
		}
	}
}

堆的创建和堆的排序

`void HeapSort(int* a, int n)
{
	int end = n - 1;
	//向上建堆
	for (int i =0 ; i < n; i++)
	{
		AdjustUp(a, i);
	}
	//向下建堆
	/*for (int i = (end - 1) / 2; i >= 0 ;i--)
	{
		AdjustDown(a, i, n);
	}*

while (end>=1)
	{
		swap(&a[0], &a[end]);
		AdjustDown(a, 0,end);
		end--;
	}
}

习题：求前K个最大或最小的元素（数量多的情况下）

void AdjustUp(int* a, int child)
{
	int parent = (child - 1) / 2;
	while ( child > 0 )
	{
		if (a[parent] > a[child])
		{
			swap(&a[parent], &a[child]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

void AdjustDown(int* a,int parent,int n)
{
	int child = parent * 2 + 1;
	for(int child = parent * 2 + 1; child <n; child=child*2+1)
	
	{
		if (child + 1 < n && a[child]  > a[child + 1])//这里注意大小堆的区别 小堆选小 大堆选大
		{
			child++;
		}
		if (a[child] < a[parent])
		{
			swap(&a[child], &a[parent]);
			parent = child;
		}
		else
		{
			break;
		}
	}
}

void HeapSort(int* a, int n,int k)
{
	int end = n - 1;
	//向上建堆
	int i = 0;
	for (i =0 ; i < k; i++)
	{
		AdjustUp(a, i);
	}
	//向下建堆
	/*for (int i = (end - 1) / 2; i >= 0 ;i--)
	{
		AdjustDown(a, i, n);
	}*/

	//求前k个最大数建k次小堆，与小堆堆顶相比，
	//比堆顶大就向下调整
	while (i < n)
	{
		if (a[0] < a[i])
		{
			swap(&a[0], &a[i]);
			AdjustDown(a, 0, k);
		}
		i++;
	}
}