LeetCode 热题 HOT 100

105. 从前序与中序遍历序列构造二叉树

题目： 给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，
请构造二叉树并返回其根节点。
示例 1：
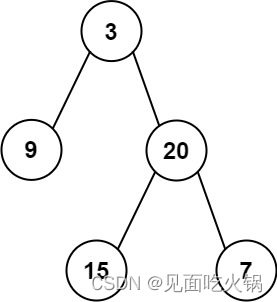
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

package ricky.com.Hot100;

import java.util.HashMap; 

/**
 * @Author xdg
 */
public class buildTree {
    /*105. 从前序与中序遍历序列构造二叉树
    给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，
    请构造二叉树并返回其根节点。*/

    // 定义二叉树节点的结构
    public class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;

        TreeNode() {
        }

        TreeNode(int val) {
            this.val = val;
        }

        TreeNode(int val, TreeNode left, TreeNode right) {
            this.val = val;
            this.left = left;
            this.right = right;
        }
    }

    class Solution {
        // 声明一个 HashMap，用于存储中序遍历数组中每个元素的索引
        HashMap<Integer, Integer> map = new HashMap<>();

        // 构建二叉树的函数，参数为先序遍历数组和中序遍历数组
        public TreeNode buildTree(int[] preorder, int[] inorder) {
            // 将中序遍历数组中每个元素的值和索引存储到 HashMap 中
            for (int i = 0; i < inorder.length; i++) {
                map.put(inorder[i], i);
            }

            // 调用递归函数构建二叉树，返回根节点
            return f(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);
        }

        // 递归函数，参数为先序遍历数组、中序遍历数组、以及它们在当前递归层次下的边界
        private TreeNode f(int[] preorder, int l1, int r1, int[] inorder, int l2, int r2) {
            // 如果左边界大于右边界，说明当前子树为空，返回 null
            if (l1 > r1) {
                return null;
            }

            // 构建当前子树的根节点
            TreeNode root = new TreeNode(preorder[l1]);
            // 在中序遍历数组中找到根节点的位置
            int i = map.get(preorder[l1]);
            // 递归构建左子树，左子树的元素范围为 preorder[l1+1, l1+i-l2] 和 inorder[l2, i-1]
            root.left = f(preorder, l1 + 1, l1 + i - l2, inorder, l2, i - 1);
            // 递归构建右子树，右子树的元素范围为 preorder[l1+i-l2+1, r1] 和 inorder[i+1, r2]
            root.right = f(preorder, l1 + i - l2 + 1, r1, inorder, i + 1, r2);
            // 返回当前子树的根节点
            return root;
        }
    }
}

114. 二叉树展开为链表

题目：给你二叉树的根结点 root ，请你将它展开为一个单链表：
展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。
**示例 1：

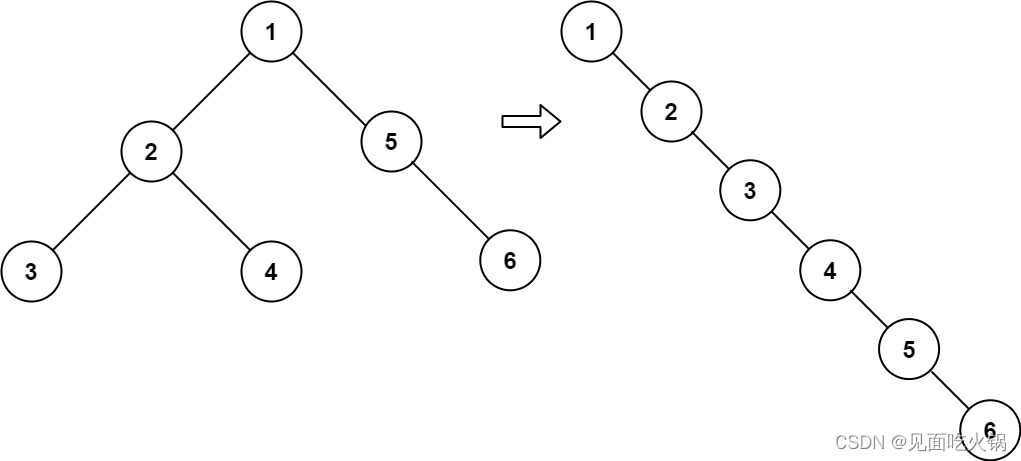
输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

思路分析： 首先对二叉树进行先序遍历，将遍历结果存储到 List 中。然后遍历 List 中的节点，构建链表。具体来说，将 List 的第一个节点作为新的根节点，并将其左指针置为 null。然后定义一个指针 cur，初始时指向新的根节点，遍历 List 中的剩余节点，将当前节点的右指针指向下一个节点，将左指针置为 null，然后将指针 cur 指向当前节点，重复上述过程，直到遍历完所有节点为止。最后返回即可。

class Solution {
    List<TreeNode> list = new ArrayList<>(); // 声明一个 List，用于存储先序遍历的结果

    // 将二叉树拉平为链表的函数，参数为二叉树的根节点
    public void flatten(TreeNode root) {
        if (root == null) { // 如果根节点为空，直接返回
            return;
        }

        preOrder(root); // 对二叉树进行先序遍历，将结果存储到 List 中
        TreeNode newRoot = list.get(0); // 获取二叉树拉平后的新根节点
        newRoot.left = null; // 将新根节点的左指针置为 null
        TreeNode cur = newRoot; // 定义一个指针，指向当前处理的节点
        for (int i = 1; i < list.size(); i++) { // 遍历 List 中的节点，构建链表
            cur.right = list.get(i); // 当前节点的右指针指向下一个节点
            cur.left = null; // 当前节点的左指针置为 null
            cur = cur.right; // 将指针指向下一个节点
        }

        return;

    }

    // 递归函数，对二叉树进行先序遍历，并将结果存储到 List 中
    private void preOrder(TreeNode root) {
        if (root == null) { // 如果当前节点为空，直接返回
            return;
        }

        list.add(root); // 将当前节点加入到 List 中
        preOrder(root.left); // 递归遍历左子树
        preOrder(root.right); // 递归遍历右子树
    }
}

124. 二叉树中的最大路径和

题目：路径 被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径
序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ，返回其 最大路径和 。。
**示例 1：

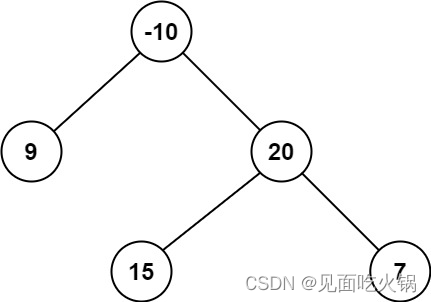
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

思路分析： 使用后序遍历的方式遍历二叉树，并计算以每个节点为路径起点的最大路径和。对于每个节点，先递归遍历其左右子树，并计算出左右子树的最大路径和。然后，以当前节点为路径起点，计算当前节点的最大路径和，即计算当前节点的值加上左子树的最大路径和和右子树的最大路径和的和，以及当前节点的值与左右子树的最大路径和相加的和中的最大值。最后，更新全局最大路径和为当前路径的最大值，即 Math.max(res, Math.max(temp, root.val + left + right))。最终，返回全局最大路径和 res。

class Solution {
    int res = Integer.MIN_VALUE; // 定义全局变量，用于保存最大路径和

    public int maxPathSum(TreeNode root) {
        if (root == null) { // 如果根节点为空，返回0
            return 0;
        }

        postOrder(root); // 对树进行后序遍历，计算最大路径和
        return res; // 返回最大路径和
    }

    // 后序遍历二叉树，并计算以当前节点为起点的最大路径和
    private int postOrder(TreeNode root) {
        if (root == null) { // 如果当前节点为空，返回0
            return 0;
        }

        // 分别对左子树和右子树进行后序遍历，并计算左子树和右子树的最大路径和
        int left = postOrder(root.left);
        int right = postOrder(root.right);

        // 计算以当前节点为起点的最大路径和，并更新全局最大路径和
        int temp = Math.max(root.val, root.val + Math.max(left, right)); // 计算以当前节点为起点的路径
        res = Math.max(res, Math.max(temp, root.val + left + right)); // 更新全局最大路径和

        // 返回以当前节点为起点的最大路径和
        return temp;
    }
}