您现在的位置是:首页 >学无止境 >C语言——数据在内存中的存储(未完待续)网站首页学无止境
C语言——数据在内存中的存储(未完待续)
文章目录
一、数据类型的介绍
无符号整形就是把有符号的取值范围合并,就是无符号整形的取值范围
| 数据类型 | 字节数 | 取值范围 |
|---|---|---|
| int | 4 | -2147483648~2147483647 |
| short | 2 | -32768~32768 |
| lomg | 8 | -2147483648~2147483647 |
| long long | 8 | -9223372036854775808~9223372036854775807 |
| char | 1 | -128~127 |
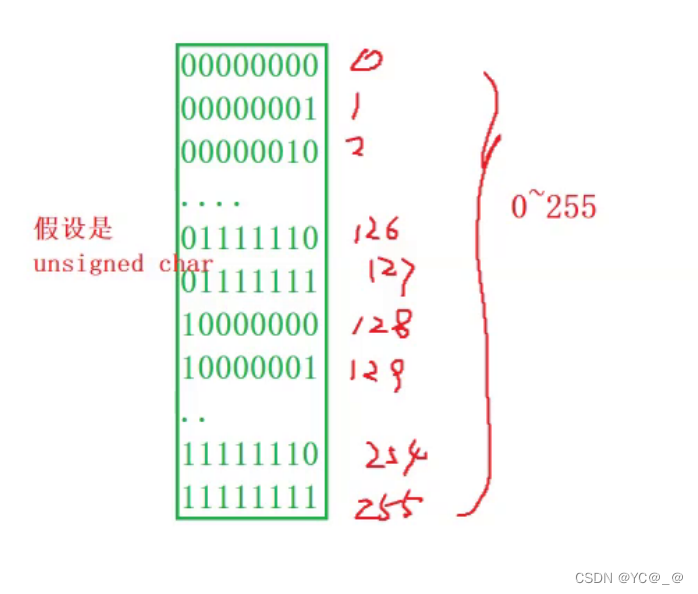
| unsigned char | 1 | 0~255 |
| unsigned int | 4 | 0~4294967295 |
| unsigned shor | 2 | 0~65535 |
| unsigned long | 8 | 0~4294967295 |
| unsigned long long | 8 | 0~1844674407309551615 |
| float | 4 | 1.1754910-38~3.402821038 |
| double | 8 | 2.2250710-308~1.7976910308 |
| long double | 12 | 2.2250710-308~1.7976910308 |
类型的意义:使用这个类型开辟内存空间的大小(大小决定了使用范围)
浮点型没有有符号跟无符号区别
在无符号类型中,假如原码是0001是无符号数,这四个都是没有符合位,假如转反码都可以取反1110。
1.0、有符号跟无符号计算原理
有符号的取值范围计算
正数原码就是补码,负数补码转反码然后原码
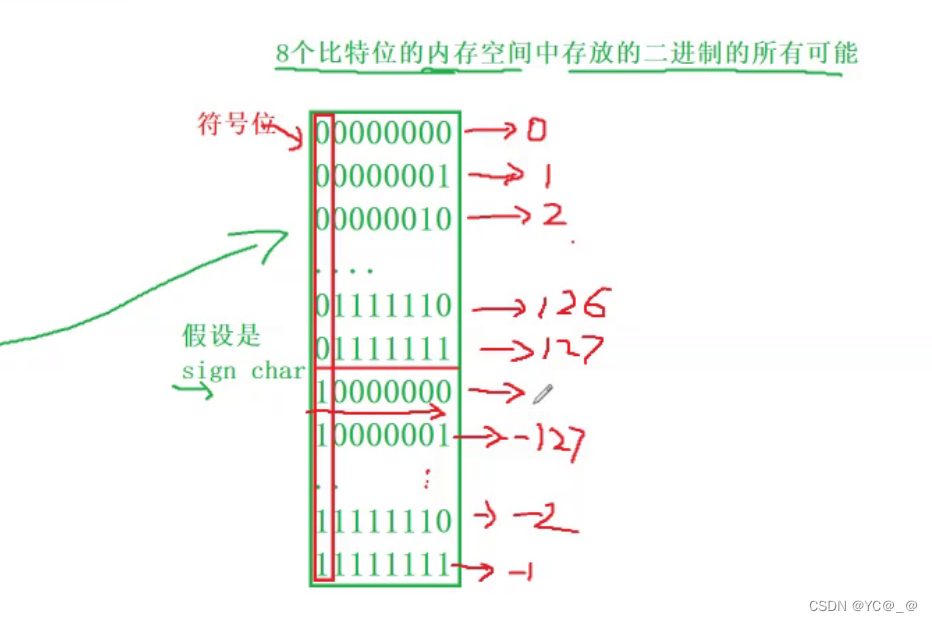
无符号的取值范围计算
无符号正数补码就是原码
假如是char类型,在不断+1过程中可以发现规律,到了-128时+1最高位会因为只能放8个字节而丢失最高位,会原回到原来的0,所以会不断的循环

1.1、数据类型的基本分类
数据类型也分为整形家族与浮点型家族
整形家族:
char
unsigned char
signed char
short
unsigned short [int]
signed short [int]
int
unsigned int
signed int
long
unsigned long [int]
signed long [int]
浮点型家族:
float
double
构造类型:
数组类型
结构体类型 struct
枚举类型 enum
联合类型 union
指针类型:
int * pi;
char * pc;
float * pf;
void * pv;
空类型
void 表示空类型(无类型)
通常应用于函数的返回类型、函数的参数、指针类型
二、整形与浮点型在内存中的存储
1.整型
数据类型决定了所开辟空间的大小,知道了数据决定空间的大小,接下来就来了解,数据在内存中是怎么存储,来继续往下看。
数据内存是用补码进行存储
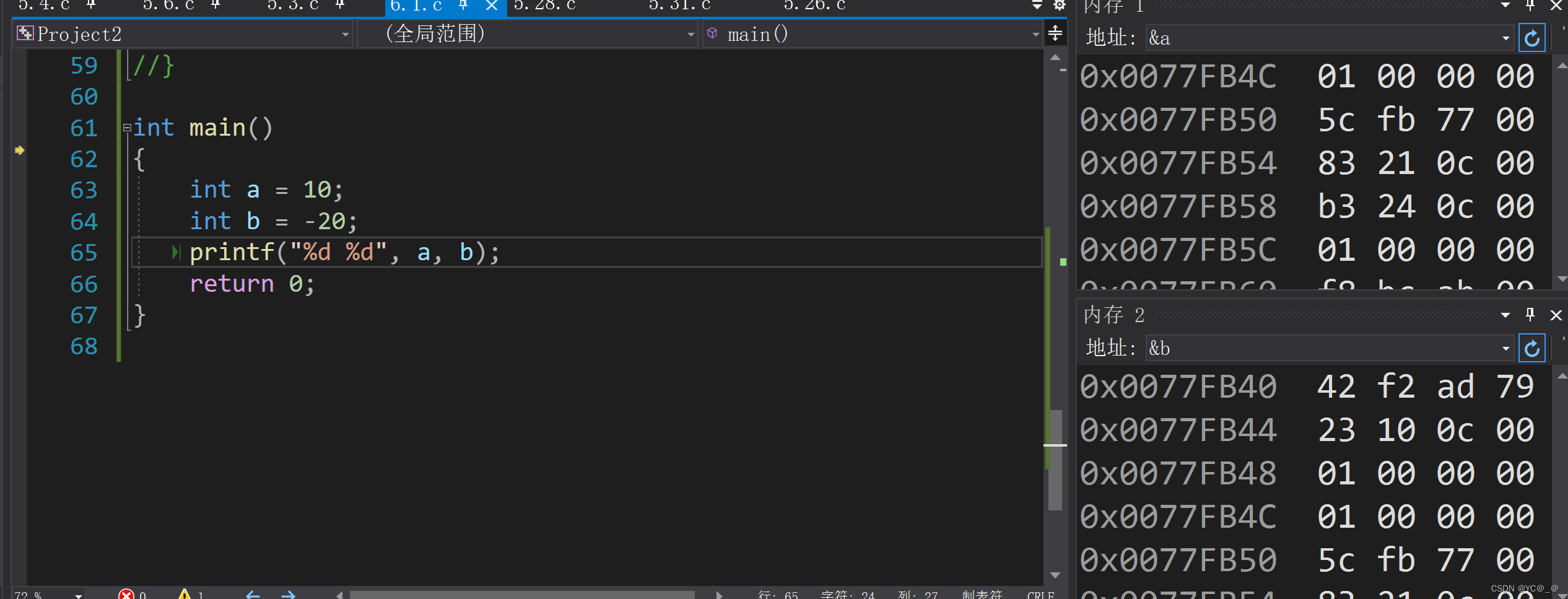
内存的显示为十六进制
可以看出补码的存储顺序相反,接下来又引申出了大端跟小端。
练习
整形提升练习一:
整型提升根据数据类型的符号位提升
int main()
{
char a = -1;
//10000000000000000000000000000001
//11111111111111111111111111111110
//11111111111111111111111111111111-截断 //a存储的-1是整型,而a类型却是char,整型占四个字节,char却是一个字节,整型存放进char就需要截断。
//11111111 -a
//11111111111111111111111111111111
//11111111111111111111111111111110
//10000000000000000000000000000001--> -1
signed char b = -1; //11111111111111111111111111111111
//11111111 -b
unsigned char c = -1;
//11111111 -c
//00000000000000000000000011111111
printf("a=%d,b=%d,c=%d", a, b, c);
//%d - 十进制的形式打印有符号整型整数
//整型提升
return 0;
}
练习二:
int main()
{
char a = -128;
//-128
//10000000000000000000000010000000
//11111111111111111111111101111111
//11111111111111111111111110000000
//-128的补码
//10000000
//11111111111111111111111110000000
printf("%u
", a);
return 0;
}
练习三:
int main()
{
//无符号整型恒大于等于0
//在无符号数迭代成-1时,将会是一个非常大的正数
unsigned int i;
for(i = 9; i >= 0; i--)
{
printf("%u
", i);
Sleep(1000);//单位是毫秒
}
return 0;
}
练习四:
a[i]里面的值会不断-1-i,直到-128为止,又因为char取值范围,前面有图char到了-128时在-1会去掉最高位会回到0,之后会不断在**-1 —— -128 —— 0 —— 127**,总共长度为256,直接不断重复循环
int main()
{
//char取值范围-128~127
//a[i]里面的值会不断-1-i,直到-128为止,又因为char取值范围,前面有图char到了-128时在-1会去掉最高位
char a[1000];
int i;
for (i = 0; i < 1000; i++)
{
a[i] = -1 - i;
}
//strlen取�之前的长度为255
printf("%d", strlen(a));
return 0;
}
1.0、大小端的介绍
什么大端小端:
大端字节序存储,把一个低位的数据内容,存放在低地址处,把一个高位的数据内容,存放在高地址处
小端字节序存储,把一个低位的数据内容,存放在高地址处,把一个高位的数据内容,存放在低地址处
字节序:是以字节为单位,讨论存储顺序
int main()
{
int a = 0x11223344;
return 0;
}
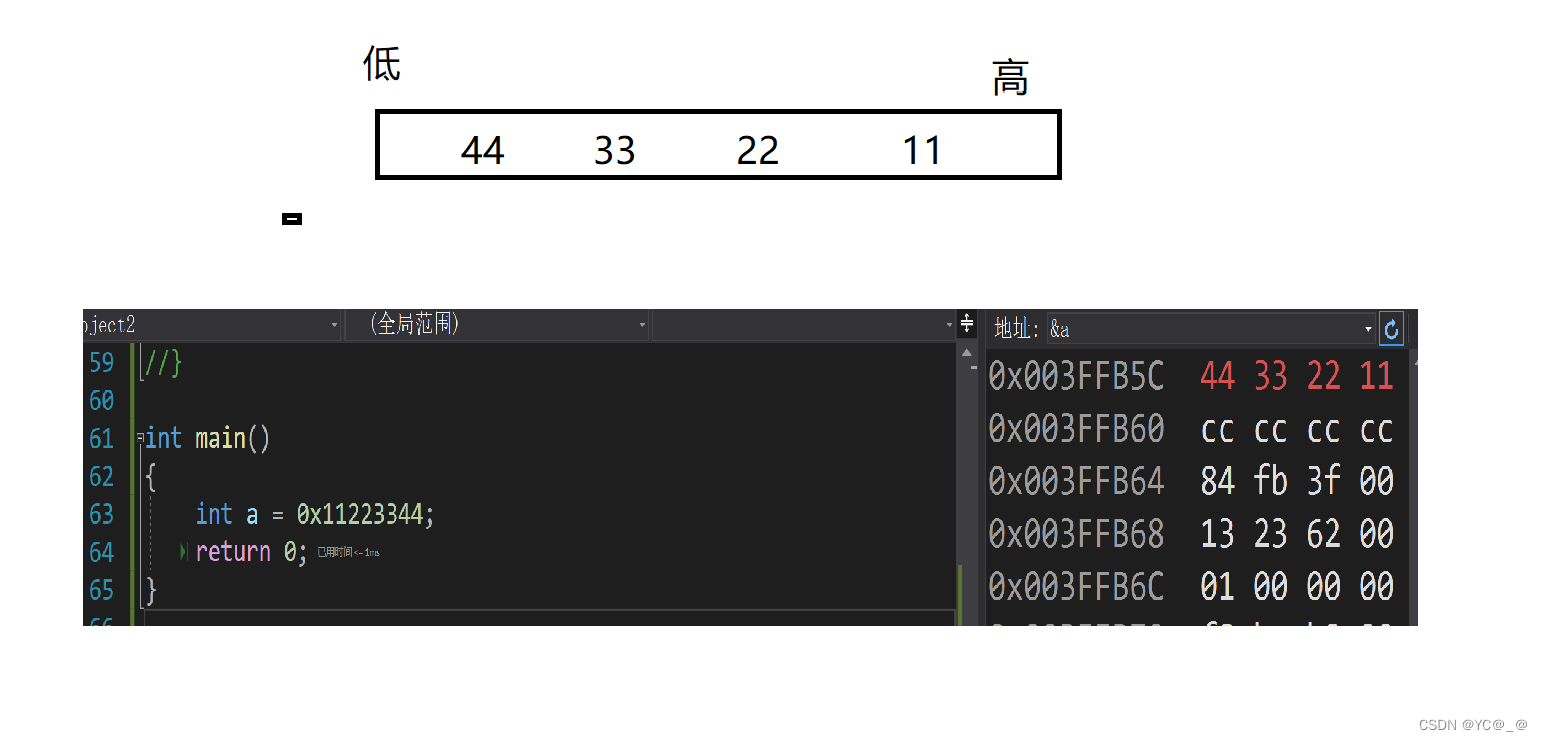
练习:
判断当前机器的字节序
#include <stdio.h>
int check_sys()
{
int i = 1;
//原类型可以访问4个字节,而程序只需要访问一个字节,所以先&a在转换成*char,又因为*成可以解引用内存
//考虑优先级
return (*(char *)&i);
}
int main()
{
int ret = check_sys();
if(ret == 1)
{
printf("小端
");
}
else
{
printf("大端
");
}
return 0;
}
2.原码、反码、补码
接下来补充一下原码、反码、补码的知识,在计算机中的整数有三种表示方法,原码、反码、补码。
三种表示方法均有符号位和数值位两部分,符号位都是用0表示“正”,用1表示“负”。
正数原、反、补相同,负数需要把原码转为反跟补码
int main()
{
//正数
int num = 10;//创建一个整型变量,叫num,这时num向内存申请4个字节来存放数据
//4个字节-32比特位
//00000000000000000000000000001010-原码
//00000000000000000000000000001010-反码
//00000000000000000000000000001010-补码
//二进制先换成十进制然后在换成十六进制,因为为了调试时内存的显示的是十六进制
//4个二进制位等于1个bit位,8个比特位等于一个字节
//负数
int num2 = -10;
//10000000000000000000000000001010 - 原码
//11111111111111111111111111110101 - 反码
//11111111111111111111111111110110 - 补码
return 0;
}
计算时补码的原理
在计算机系统中,数值一律用补码来表示和存储。原因在于,使用补码,可以将符号位和数值域统
一处理;
同时,加法和减法也可以统一处理(CPU只有加法器)此外,补码与原码相互转换,其运算过程是相同的,不需要额外的硬件电路。
//计算1-1
//1+(-1)
// 00000000000000000000000000000001 --> 1的补码
// 11111111111111111111111111111111 --> -1的补码
// 00000000000000000000000000000000
//
// 原码计算是错误的
//00000000000000000000000000000001
//10000000000000000000000000000001
//10000000000000000000000000000010---> -2
2.0、原码
原码就是二进制
2.1、反码
原码按位取反得到反码,符号位不变
2.2、补码
在反码右边第一位+1满2为0进1位,符号位不变
2.3、补码转原码第二种方法
补码、取反、+1得到补码
有符号
补码:111111111111111111111111111111110110
取反:10000000000000000000000000001001
+1 : 10000000000000000000000000001010






 U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) Allegro16.6差分等长设置及走线总结
Allegro16.6差分等长设置及走线总结