LC-1377. T 秒后青蛙的位置（DFS、BFS）网站首页 技术杂谈

LC-1377. T 秒后青蛙的位置（DFS、BFS）

Miraclo_acc 2024-06-23 18:01:02

简介LC-1377. T 秒后青蛙的位置（DFS、BFS）

1377. T 秒后青蛙的位置

难度困难57

给你一棵由 n 个顶点组成的无向树，顶点编号从 1 到 n。青蛙从 顶点 1 开始起跳。规则如下：

在一秒内，青蛙从它所在的当前顶点跳到另一个 未访问 过的顶点（如果它们直接相连）。
青蛙无法跳回已经访问过的顶点。
如果青蛙可以跳到多个不同顶点，那么它跳到其中任意一个顶点上的机率都相同。
如果青蛙不能跳到任何未访问过的顶点上，那么它每次跳跃都会停留在原地。

无向树的边用数组 edges 描述，其中 edges[i] = [ai, bi] 意味着存在一条直接连通 ai 和 bi 两个顶点的边。

返回青蛙在 t 秒后位于目标顶点 target 上的概率。与实际答案相差不超过 10-5 的结果将被视为正确答案。

示例 1：

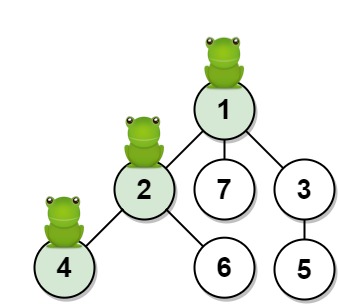
输入：n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4
输出：0.16666666666666666 
解释：上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳，第 1 秒 有 1/3 的概率跳到顶点 2 ，然后第 2 秒 有 1/2 的概率跳到顶点 4，因此青蛙在 2 秒后位于顶点 4 的概率是 1/3 * 1/2 = 1/6 = 0.16666666666666666 。

示例 2：

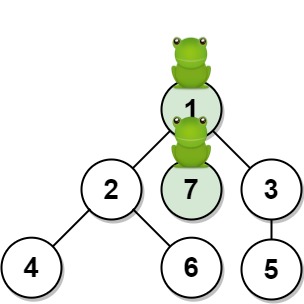
输入：n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 1, target = 7
输出：0.3333333333333333
解释：上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳，有 1/3 = 0.3333333333333333 的概率能够 1 秒 后跳到顶点 7 。

提示：

1 <= n <= 100
edges.length == n - 1
edges[i].length == 2
1 <= ai, bi <= n
1 <= t <= 50
1 <= target <= n

BFS模拟

BFS模拟，在遍历每个节点时，先查看当前节点的邻接节点是不是都访问过了，如果都访问过了，说明走不动了，原地踏步，将该节点加入到队列中，不然就将没访问过的节点加入到队列中。一共循环t次，最后找队列中值 = target的元素

class Solution {
    public double frogPosition(int n, int[][] edges, int t, int target) {
        if(n == 1 && t == target) return 1.0;
        if(n == 1 && t != target) return 0.0;
        List<Integer>[] g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList<>());
        for(int[] e : edges){
            int x = e[0]-1, y = e[1]-1;
            g[x].add(y);
            g[y].add(x);
        }
        target--;
        Deque<Pair<Integer, Double>> dq = new ArrayDeque<>();
        boolean[] vis = new boolean[n];
        dq.addLast(new Pair<>(0, 1.0));
        vis[0] = true;
        int step = 0;
        while(!dq.isEmpty()){
            int size = dq.size();
            while(size-- > 0){
                Pair<Integer, Double> p = dq.pollFirst();
                int s = g[p.getKey()].size();
                for(int y : g[p.getKey()]){
                    if(vis[y])
                        s -= 1;
                }
                if(s == 0) dq.addLast(p);
                else{
                    for(int y : g[p.getKey()]){
                        if(!vis[y]){
                            vis[y] = true;
                            dq.addLast(new Pair<>(y, p.getValue() * (1.0 / s)));
                        }
                    }
                }
            }
            step += 1;
            if(step == t) break;
        }
        while(!dq.isEmpty()){
            Pair<Integer, Double> p = dq.pollFirst();
            if(p.getKey() == target){
                return p.getValue();
            }
        }
        return 0.0;
    }
}

DFS递归（自顶向下 + 自底向上）

https://leetcode.cn/problems/frog-position-after-t-seconds/solution/dfs-ji-yi-ci-you-qu-de-hack-by-endlessch-jtsr/

既然答案是由若干分子为 1 的分数相乘得到，那么干脆只把分母相乘，最后再计算一下倒数，就可以避免因浮点乘法导致的精度丢失了。另外，整数的计算效率通常比浮点数的高。

自顶向下是一边[递]，一边把儿子个数 c 乘起来，如果能在第 t 秒到达 target，或者小于t 秒到达 target 且 target 是叶子节点(此时每次跳跃都会停留在原地) ，那么就记录答案为乘积的倒数，同时返回一个布尔值表示递归结束
**自底向上的思路是类似的，找到 target 后，在[归]的过程中做乘法。**个人更喜欢这种写法，因为只在找到 target 之后才做乘法，而自顶向下即使在不含 target 的子树中搜索，也会盲目地做乘法

技巧：
可以把节点 1 添加一个 0 号邻居，从而避免判断当前节点为根节点1，也避免了特判 n = 1的情况

此外，DFS 中的时间不是从 0 开始增加到 t，而是从 leftT = t 开始减小到 0，这样代码中只需和 0 比较，无需和 t 比较，从而减少一个DFS 之外变量的引入。

自顶向下：（递）

class Solution:
    def frogPosition(self, n: int, edges: List[List[int]], t: int, target: int) -> float:
        g = [[] for _ in range(n + 1)]
        g[1] = [0]  # 减少额外判断的小技巧
        for x, y in edges:
            g[x].append(y)
            g[y].append(x)  # 建树
        ans = 0

        def dfs(x: int, fa: int, left_t: int, prod: int) -> True:
            # t 秒后必须在 target（恰好到达，或者 target 是叶子停在原地）
            if x == target and (left_t == 0 or len(g[x]) == 1):
                nonlocal ans 
                ans = 1 / prod
                return True
            if x == target or left_t == 0: return False
            for y in g[x]: # 遍历 x 的儿子 y
                if y != fa and dfs(y, x, left_t-1, prod * (len(g[x]) - 1)):
                    return True # 找到 target 就不再递归了
            return False # 未找到target

        dfs(1, 0, t, 1)
        return ans

自底向上：（归）

class Solution:
    def frogPosition(self, n: int, edges: List[List[int]], t: int, target: int) -> float:
        g = [[] for _ in range(n + 1)]
        g[1] = [0]  # 减少额外判断的小技巧
        for x, y in edges:
            g[x].append(y)
            g[y].append(x)  # 建树
        ans = 0

        def dfs(x: int, fa: int, left_t: int) -> True:
            # t 秒后必须在 target（恰好到达，或者 target 是叶子停在原地）
            if left_t == 0:
                return x == target
            if x == target:
                return len(g[x]) == 1
            for y in g[x]: # 遍历 x 的儿子 y
                if y != fa: 
                    prod = dfs(y, x, left_t-1) # 寻找 target
                    if prod:
                        return prod * (len(g[x]) - 1)  # 乘上儿子个数，并直接返回
            return 0 # 未找到target

        prod = dfs(1, 0, t)
        return 1 / prod if prod else 0