您现在的位置是：首页 >技术教程 >LeetCode高频算法刷题记录8网站首页技术教程

LeetCode高频算法刷题记录8

Frankenstein@ 2024-06-18 08:04:32
简介LeetCode高频算法刷题记录8

文章目录

1. 零钱兑换【中等】

题目链接：https://leetcode.cn/problems/coin-change/
参考题解：https://leetcode.cn/problems/coin-change/solution/322-ling-qian-dui-huan-by-leetcode-solution/

1.1 题目描述

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

你可以认为每种硬币的数量是无限的。

示例1：

输入：coins = [1, 2, 5], amount = 11
输出：3
解释：11 = 5 + 5 + 1

示例2：

输入：coins = [2], amount = 3
输出：-1

示例3：

输入：coins = [1], amount = 0
输出：0

提示：

  • 1 <= coins.length <= 12
  • 1 <= coins[i] <= 2^31 - 1
  • 0 <= amount <= 10^4

1.2 解题思路

1.3 代码实现

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        vector<int> ans(amount + 1, amount + 1);
        int len = coins.size();
        ans[0] = 0;
        for(int i = 1; i <= amount; i++) {
            for(int j = 0; j < len; j++) {
                if(coins[j] <= i)
                    ans[i] = min(ans[i], ans[i - coins[j]] + 1);
            }
        }
        return ans[amount] > amount ? -1 : ans[amount];
    }
};

2. 最小栈【最小栈】

题目链接：https://leetcode.cn/problems/min-stack/
参考题解：https://leetcode.cn/problems/min-stack/solution/zui-xiao-zhan-by-leetcode-solution/

2.1 题目描述

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

实现 MinStack 类:

  • MinStack() 初始化堆栈对象。
  • void push(int val) 将元素val推入堆栈。
  • void pop() 删除堆栈顶部的元素。
  • int top() 获取堆栈顶部的元素。
  • int getMin() 获取堆栈中的最小元素。

示例1：

输入：
[“MinStack”,“push”,“push”,“push”,“getMin”,“pop”,“top”,“getMin”]
[[],[-2],[0],[-3],[],[],[],[]]
输出：
[null,null,null,null,-3,null,0,-2]
解释：
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.getMin(); --> 返回 -2.

提示：

  • -2^31 <= val <= 2^31 - 1
  • pop、top 和 getMin 操作总是在 非空栈 上调用
  • push, pop, top, and getMin最多被调用 3 * 10^4 次

2.2 解题思路

2.3 代码实现

class MinStack {
public:
    stack<int> stk;
    stack<int> auxStk;
    MinStack() {
        auxStk.push(INT_MAX);
    }
    
    void push(int val) {
        stk.push(val);
        auxStk.push(min(auxStk.top(), val));
    }
    
    void pop() {
        stk.pop();
        auxStk.pop();
    }
    
    int top() {
        return stk.top();
    }
    
    int getMin() {
        return auxStk.top();
    }
};

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack* obj = new MinStack();
 * obj->push(val);
 * obj->pop();
 * int param_3 = obj->top();
 * int param_4 = obj->getMin();
 */

3. 最长有效括号【困难】

题目链接：https://leetcode.cn/problems/longest-valid-parentheses/
参考题解：https://leetcode.cn/problems/longest-valid-parentheses/solution/zui-chang-you-xiao-gua-hao-by-leetcode-solution/

3.1 题目描述

给你一个只包含 ‘(’ 和 ‘)’ 的字符串，找出最长有效（格式正确且连续）括号子串的长度。

示例1：

输入：s = “(()”
输出：2
解释：最长有效括号子串是 “()”

示例2：

输入：s = “)()())”
输出：4
解释：最长有效括号子串是 “()()”

示例3：

输入：s = “”
输出：0

提示：

  • 0 <= s.length <= 3 * 10^4
  • s[i] 为 ‘(’ 或 ‘)’

3.2 解题思路

3.3 代码实现

class Solution {
public:
    int longestValidParentheses(string s) {
        stack<int> stk;
        stk.push(-1);
        int ans = 0;
        int len = s.length();
        for(int i = 0; i < len; i++) {
            if(s[i] == '(') {
                stk.push(i);
            }
            else {
                stk.pop();
                if(!stk.empty()) {
                    ans = max(ans, i - stk.top());
                }
                else
                    stk.push(i);
            }
        }
        return ans;
    }
};

4. 从前序与中序遍历序列构造二叉树【中等】

题目链接：https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/
参考题解：https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/solution/cong-qian-xu-yu-zhong-xu-bian-li-xu-lie-gou-zao-9/

4.1 题目描述

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例1：
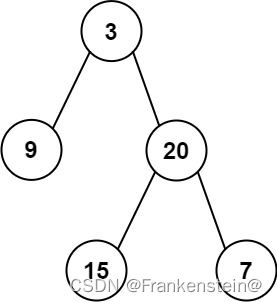
在这里插入图片描述

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例2：

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示：

  • 1 <= preorder.length <= 3000
  • inorder.length == preorder.length
  • -3000 <= preorder[i], inorder[i] <= 3000
  • preorder 和 inorder 均 无重复 元素
  • inorder 均出现在 preorder
  • preorder 保证 为二叉树的前序遍历序列
  • inorder 保证 为二叉树的中序遍历序列

4.2 解题思路

4.3 代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    unordered_map<int, int> find_root;
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder, int pre_start, int pre_end, int in_start, int in_end) {
        if(pre_start > pre_end)
            return nullptr;
        int pre_root = pre_start;
        int in_root = find_root[preorder[pre_root]];
        int left_tree_len = in_root - in_start;
        TreeNode* root = new TreeNode(inorder[in_root]);
        root->left = buildTree(preorder, inorder, pre_root + 1, pre_root + left_tree_len, in_start, in_root - 1);
        root->right = buildTree(preorder, inorder, pre_root + left_tree_len + 1, pre_end, in_root + 1, in_end);
        return root;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        for(int i = 0; i < inorder.size(); i++)
            find_root[inorder[i]] = i;
        return buildTree(preorder, inorder, 0, preorder.size() - 1, 0, inorder.size() - 1);
    }
};

5. 子集【中等】

题目链接：https://leetcode.cn/problems/subsets/
参考题解：https://leetcode.cn/problems/subsets/solution/zi-ji-by-leetcode-solution/

5.1 题目描述

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

示例1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例2：

输入：nums = [0]
输出：[[],[0]]

提示：

  • 1 <= nums.length <= 10
  • -10 <= nums[i] <= 10
  • nums 中的所有元素 互不相同

5.2 解题思路

5.3 代码实现

class Solution {
public:
    vector<int> sub;
    vector<vector<int>> ans;
    void chooseNum(vector<int>& nums, int current) {
        if(current == nums.size()) {
            ans.push_back(sub);
            return;
        }
        chooseNum(nums, current + 1);
        sub.push_back(nums[current]);
        chooseNum(nums, current + 1);
        sub.pop_back();
    }
    vector<vector<int>> subsets(vector<int>& nums) {
        chooseNum(nums, 0);
        return ans;
    }
};
风语者！平时喜欢研究各种技术，目前在从事后端开发工作，热爱生活、热爱工作。

站长推荐