矩阵乘法的例子1

以下例来说明backward中参数gradient的作用

注意在本文中@表示矩阵乘法，*表示对应元素相乘

求A求偏导

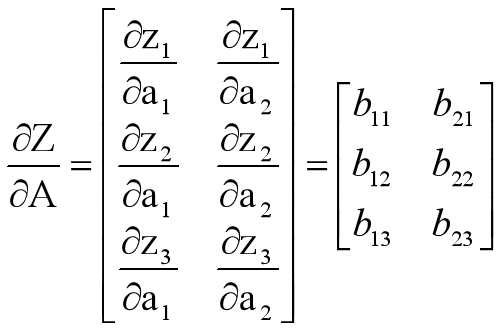
试运行代码1

import torch

# [1,2]@[2*3]=[1,3]
A = torch.tensor([[1., 2.]], requires_grad=True)
B = torch.tensor([[10., 20., 30.], [100., 200., 300.]], requires_grad=True)
Z = A @ B

Z.backward()  # dz1/dx1, dz2/dx1

运行结果1

Traceback (most recent call last):
  File "D:SoftProgramJetBrainsPyCharm Community Edition 2023.1pluginspython-cehelperspydevpydevd.py", line 1496, in _exec
    pydev_imports.execfile(file, globals, locals)  # execute the script
  File "D:SoftProgramJetBrainsPyCharm Community Edition 2023.1pluginspython-cehelperspydev\_pydev_imps\_pydev_execfile.py", line 18, in execfile
    exec(compile(contents+" ", file, 'exec'), glob, loc)
  File "E:programpythonBili_deep_thoughtsRNNhelph_backward_5.py", line 12, in <module>
    Z.backward()  # dz1/dx1, dz2/dx1
  File "D:SoftProgramJetBrainsanaconda3_202303libsite-packages orch\_tensor.py", line 396, in backward
    torch.autograd.backward(self, gradient, retain_graph, create_graph, inputs=inputs)
  File "D:SoftProgramJetBrainsanaconda3_202303libsite-packages orchautograd\__init__.py", line 166, in backward
    grad_tensors_ = _make_grads(tensors, grad_tensors_, is_grads_batched=False)
  File "D:SoftProgramJetBrainsanaconda3_202303libsite-packages orchautograd\__init__.py", line 67, in _make_grads
    raise RuntimeError("grad can be implicitly created only for scalar outputs")
RuntimeError: grad can be implicitly created only for scalar outputs

查到错误原因

如果 Tensor 是一个标量(即它包含一个元素的数据），则不需要为 backward() 指定任何参数，但是如果它有更多的元素，则需要指定一个 gradient 参数，该参数是形状匹配的张量。

看完有一点了解，但是不太明白“该参数是形状匹配的张量”。

尝试修改代码2

import torch

# [1,2]@[2*3]=[1,3]
A = torch.tensor([[1., 2.]], requires_grad=True)
B = torch.tensor([[10., 20., 30.], [100., 200., 300.]], requires_grad=True)
Z = A @ B

Z.backward(torch.ones_like(A))  # dz1/dx1, dz2/dx1

运行结果2

Traceback (most recent call last):
  File "D:SoftProgramJetBrainsPyCharm Community Edition 2023.1pluginspython-cehelperspydevpydevd.py", line 1496, in _exec
    pydev_imports.execfile(file, globals, locals)  # execute the script
  File "D:SoftProgramJetBrainsPyCharm Community Edition 2023.1pluginspython-cehelperspydev\_pydev_imps\_pydev_execfile.py", line 18, in execfile
    exec(compile(contents+" ", file, 'exec'), glob, loc)
  File "E:programpythonBili_deep_thoughtsRNNhelph_backward_5.py", line 12, in <module>
    Z.backward(torch.ones_like(A))  # dz1/dx1, dz2/dx1
  File "D:SoftProgramJetBrainsanaconda3_202303libsite-packages orch\_tensor.py", line 396, in backward
    torch.autograd.backward(self, gradient, retain_graph, create_graph, inputs=inputs)
  File "D:SoftProgramJetBrainsanaconda3_202303libsite-packages orchautograd\__init__.py", line 166, in backward
    grad_tensors_ = _make_grads(tensors, grad_tensors_, is_grads_batched=False)
  File "D:SoftProgramJetBrainsanaconda3_202303libsite-packages orchautograd\__init__.py", line 50, in _make_grads
    raise RuntimeError("Mismatch in shape: grad_output["
RuntimeError: Mismatch in shape: grad_output[0] has a shape of torch.Size([1, 2]) and output[0] has a shape of torch.Size([1, 3])

看到这里明白了点，“该参数是形状匹配的张量”更具体的应该是“该参数是和输出Z形状匹配的张量”。

解释

由于pytorch只能对标量进行求导，对于非标量的求导，其思想是将其转换成标量，即将其各个元素相加，然后求导。
但是如果只是简单的把全部元素相加，就无法知道z2对a2的导数，因此引入gradient参数，其形状和输出Z的形状一致，gradient的参数是累加时Z中对应参数的系数，以一开始的矩阵乘法的例子1为例，即

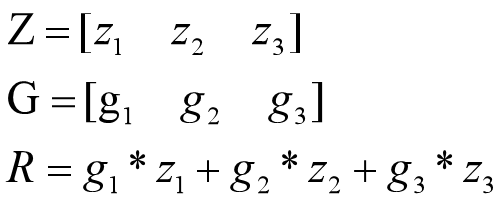
 因此矩阵Z对A的导数，就转换成了标量R对A导数，即

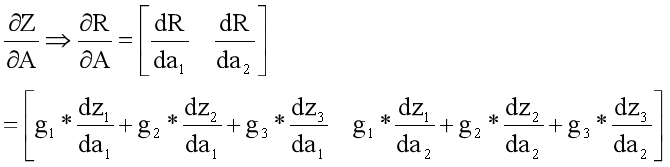
注意：对A求导的结果是A的形状

 验证

只求z1对A的导数，即G=[1,0,0]，运行代码3

import torch

# [1,2]@[2*3]=[1,3],gradient=[1,3]
A = torch.tensor([[1., 2.]], requires_grad=True)
B = torch.tensor([[10., 20., 30.], [100., 200., 300.]], requires_grad=True)
Z = A @ B

# Z.backward(torch.ones_like(A))  # dz1/dx1, dz2/dx1
Z.backward(gradient=torch.tensor([[1., 0., 0.]])) # dz1/dx1, dz2/dx1
print('Z=', Z)
print('A.grad=', A.grad)
print('B.grad=', B.grad)

运行结果3

Z= tensor([[210., 420., 630.]], grad_fn=<MmBackward0>)

A.grad= tensor([[ 10., 100.]])
B.grad= tensor([[1., 0., 0.],
        [2., 0., 0.]])

 尝试解释一下对B的导数

哈达马积的例子

代码4

import torch

# [1,3]*[2*3]=[1,3],gradient=[2,3]
A1 = torch.tensor([[1., 2., 3.]], requires_grad=True)
B1 = torch.tensor([[10., 20., 30.], [100., 200., 300.]], requires_grad=True)
Z1 = A1 * B1 
G1 = torch.zeros_like(Z1)
G1[1, 0] = 1
Z1.backward(gradient=G1)  # dz1/dx1, dz2/dx1
print('Z1=', Z1)
print('Z1.shape=', Z1.shape)
print('A1.grad=', A1.grad)
print('B1.grad=', B1.grad)
pass

运行结果4

Z1= tensor([[ 10.,  40.,  90.],
        [100., 400., 900.]], grad_fn=<MulBackward0>)
Z1.shape= torch.Size([2, 3])
A1.grad= tensor([[100.,   0.,   0.]])
B1.grad= tensor([[0., 0., 0.],
        [1., 0., 0.]])

 矩阵乘法的例子2

代码5

import torch

A11 = torch.tensor([[0.1, 0.2], [1., 2.]], requires_grad=True)
B11 = torch.tensor([[10., 20., 30.], [100., 200., 300.]], requires_grad=True)
Z11 = torch.mm(A11, B11)
J11 = torch.zeros((2, 2))
G11 = torch.zeros_like(Z11)
G11[1, 0] = 1
Z11.backward(G11, retain_graph=True)  # dz1/dx1, dz2/dx1
print('Z11=', Z11)
print('Z11.shape=', Z11.shape)
print('A11.grad=', A11.grad)
print('B11.grad=', B11.grad)
pass

运行结果5

Z11= tensor([[ 21.,  42.,  63.],
        [210., 420., 630.]], grad_fn=<MmBackward0>)
Z11.shape= torch.Size([2, 3])
A11.grad= tensor([[  0.,   0.],
        [ 10., 100.]])
B11.grad= tensor([[1., 0., 0.],
        [2., 0., 0.]])

参考

Pytorch中的.backward()方法 - 知乎

 Pytorch autograd,backward详解 - 知乎

PyTorch中的backward - 知乎

grad can be implicitly created only for scalar outputs_一只皮皮虾x的博客-CSDN博客