( 动态规划) 1035. 不相交的线 ——【Leetcode每日一题】网站首页 技术交流

( 动态规划) 1035. 不相交的线 ——【Leetcode每日一题】

酷酷的懒虫 2024-06-17 11:19:25

简介( 动态规划) 1035. 不相交的线 ——【Leetcode每日一题】

❓1035. 不相交的线

难度：中等

在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足满足：

nums1[i] == nums2[j]
且绘制的直线不与任何其他连线（非水平线）相交。

请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。

以这种方法绘制线条，并返回可以绘制的最大连线数。

示例 1：

输入：nums1 = [1,4,2], nums2 = [1,2,4]
输出：2
解释：可以画出两条不交叉的线，如上图所示。
但无法画出第三条不相交的直线，因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。

示例 2：

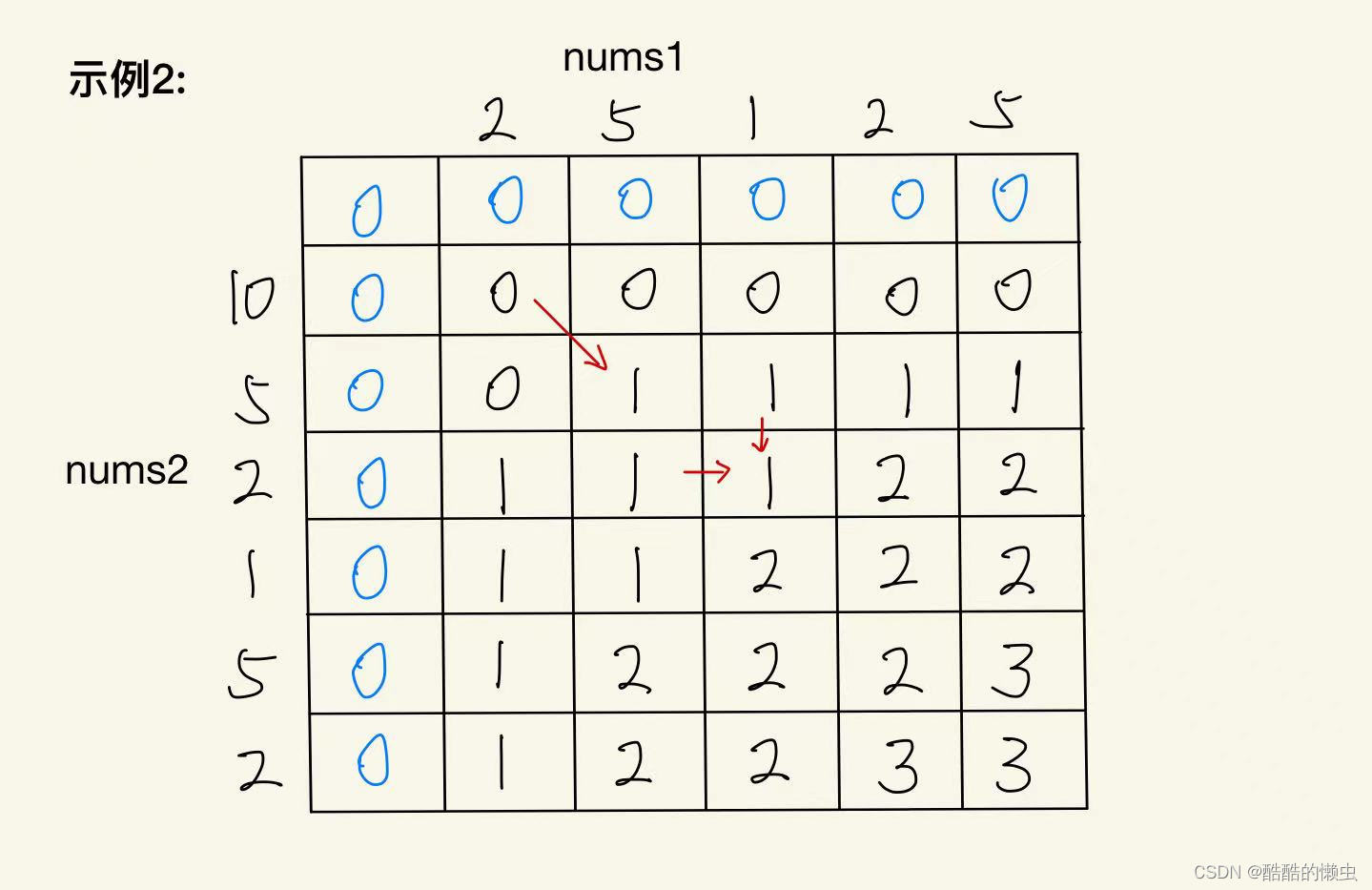
输入：nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
输出：3

示例 3：

输入：nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
输出：2

提示：

1 <= nums1.length, nums2.length <= 500
1 <= nums1[i], nums2[j] <= 2000

?思路：动态规划

由于连线不能相交，则可以只看nums2的第 i 个数字和 nums1的第 j 个数字：

如果相等，则可以直接相连：此时nums2的前 i 个数字和 nums1的前 j 个数字的连线数等于nums2的前 i - 1 个数字和 nums1的前 j - 1 个数字的连线数 + 1；
如果不相等，则不能连接：可以取nums2的前 i - 1 个数字和 nums1的前 j 个数字的连线数，或nums2的前 i 个数字和 nums1的前 j - 1 个数字的连线数 ，取两者最大值。

根据上述分析我们定义二维dp数组，dp[i][j]表示数组nums2的前 i 个数字和 nums1的前 j 个数字可以绘制的最大连线数，举例如下：

在这里插入图片描述

如果nums2[i]等于nums1[j]，nums2[i]可以与nums1[j]相连，也可以不连，则状态转移公式为：
$d p [i] [j] = d p [i - 1] [j - 1] + 1$
如果nums2[i]不等于nums1[j]，则状态转移公式为：
$d p [i] [j] = ma x (d p [i - 1] [j], d p [i] [j - 1])$

⭐️ 空间优化：

由于dp[i][j] 只与上一行和当前行有关系，所以可以进行空间优化，只需要两个一维数组 dp[2][j]即可，一个保存当前行，另一个保存当前行的上一行，状态转移公式为：

nums2[i]等于nums1[j]：
$d p [sec] [j] = d p [f i r] [j - 1] + 1$
nums2[i]不等于nums1[j]，：
$d p [sec] [j] = ma x (d p [f i r] [j], d p [sec] [j - 1])$

行号 fir和sec交替变换。

?代码：(Java、C++)

Java

class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int n = nums2.length;
        int m = nums1.length;
        int[][] dp = new int[n + 1][m + 1];
        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= m; j++){
                if(nums1[j - 1] == nums2[i - 1]){
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                else{
                    dp[i][j] = dp[i][j - 1] > dp[i - 1][j] ? dp[i][j - 1] : dp[i - 1][j];
                }
            }
        }
        return dp[n][m];
    }
}

C++

class Solution {
public:
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        int n = nums2.size();
        int m = nums1.size();
        vector<vector<int>>dp(n + 1, vector<int>(m + 1));
        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= m; j++){
                if(nums1[j - 1] == nums2[i - 1]){
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                else{
                    dp[i][j] = dp[i][j - 1] > dp[i - 1][j] ? dp[i][j - 1] : dp[i - 1][j];
                }
            }
        }
        return dp[n][m];
    }
};

⭐️空间优化

Java

class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int n = nums2.length;
        int m = nums1.length;
        int[][] dp = new int[2][m + 1];
        int fir = 0, sec = 1;
        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= m; j++){
                if(nums1[j - 1] == nums2[i - 1]){
                    dp[sec][j] = dp[fir][j - 1] + 1;
                }
                else{
                    dp[sec][j] = dp[sec][j - 1] > dp[fir][j] ? dp[sec][j - 1] : dp[fir][j];
                }
            }
            int tmp = fir;
            fir = sec;
            sec = tmp;
        }
        return Math.max(dp[0][m], dp[1][m]);
    }
}

C++

class Solution {
public:
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        int n = nums2.size();
        int m = nums1.size();
        vector<vector<int>>dp (2, vector<int>(m + 1));
        int fir = 0, sec = 1;
        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= m; j++){
                if(nums1[j - 1] == nums2[i - 1]){
                    dp[sec][j] = dp[fir][j - 1] + 1;
                }
                else{
                    dp[sec][j] = dp[sec][j - 1] > dp[fir][j] ? dp[sec][j - 1] : dp[fir][j];
                }
            }
            int tmp = fir;
            fir = sec;
            sec = tmp;
        }
        return max(dp[0][m], dp[1][m]);
    }
};