您现在的位置是：首页 >技术交流 >LeetCode高频算法刷题记录1网站首页技术交流
LeetCode高频算法刷题记录1
文章目录
1. 无重复字符的最长子串【中等】
题目链接：https://leetcode.cn/problems/longest-substring-without-repeating-characters/
参考题解：https://leetcode.cn/problems/longest-substring-without-repeating-characters/solution/wu-zhong-fu-zi-fu-de-zui-chang-zi-chuan-by-leetc-2/
1.1 题目描述
给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。
示例1：
输入: s = “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”，所以其长度为 3。
示例2：
输入: s = “bbbbb”
输出: 1
解释: 因为无重复字符的最长子串是 “b”，所以其长度为 1。
示例3：
输入: s = “pwwkew”
输出: 3
解释: 因为无重复字符的最长子串是 “wke”，所以其长度为 3。
请注意，你的答案必须是 子串 的长度，“pwke” 是一个子序列，不是子串。
提示：
- 0 <= s.length <= 5 * 104
- s 由英文字母、数字、符号和空格组成
1.2 解题思路
依次考察以字符串中每个字符 s[i] 为起始的最长子串，一个关键的性质是，随着 i 的增加，其最长子串的结束位置也在不断增加。具体来说，使用一个哈希表 repeat 来存不重复的字符，每次往 repeat 中去掉子串最左边的字符，然后再不断试探能否往右继续把子串加长，最后比较当前子串是否是历史最长子串。
1.3 代码实现
class Solution {
public:
int lengthOfLongestSubstring(string s) {
unordered_set<char> repeat;
int r = -1;
int ans = 0;
int n = s.length();
for (int i = 0; i < n; ++i) {
if (i != 0) {
repeat.erase(s[i - 1]);
}
while (r + 1 < n && !repeat.count(s[r + 1])) {
repeat.insert(s[r + 1]);
++r;
}
ans = max(ans, r - i + 1);
}
return ans;
}
};
2. 反转链表【简单】
题目链接：https://leetcode.cn/problems/reverse-linked-list/
参考题解：https://leetcode.cn/problems/reverse-linked-list/solution/fan-zhuan-lian-biao-by-leetcode-solution-d1k2/
2.1 题目描述
给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。
示例1：
输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]
示例2：
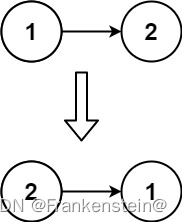
输入：head = [1,2]
输出：[2,1]
示例3：
输入：head = []
输出：[]
提示：
- 链表中节点的数目范围是 [0, 5000]
- -5000 <= Node.val <= 5000
2.2 解题思路
可以模拟一下反转的过程，捋清楚各个操作的先后顺序。为了实现某个节点 current 的反转，需要记录其前置节点，而在 current 反转后，其后继节点便丢失了，因此需要用一个临时节点 tmp 把 current 的后继节点暂时记录下来。
2.3 代码实现
/**
- Definition for singly-linked list.
- struct ListNode {
- int val;
- ListNode *next;
- ListNode() : val(0), next(nullptr) {}
- ListNode(int x) : val(x), next(nullptr) {}
- ListNode(int x, ListNode *next) : val(x), next(next) {}
- };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* pre = nullptr;
ListNode* current = head;
while (current != nullptr) {
ListNode* tmp = current -> next;
current -> next = pre;
pre = current;
current = tmp;
}
return pre;
}
};
3. LRU 缓存【中等】
题目链接：https://leetcode.cn/problems/lru-cache/
参考题解：https://leetcode.cn/problems/lru-cache/solution/lruhuan-cun-ji-zhi-by-leetcode-solution/
3.1 题目描述
请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类：
- LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
- int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
- void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该 逐出 最久未使用的关键字。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
示例：
输入
[“LRUCache”, “put”, “put”, “get”, “put”, “get”, “put”, “get”, “get”, “get”]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]
解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4
提示：
- 1 <= capacity <= 3000
- 0 <= key <= 10000
- 0 <= value <= 105
- 最多调用 2 * 105 次 get 和 put
3.2 解题思路
用双向链表模拟缓存，越靠近头部表示越近使用过，越靠近尾部表示越久未使用。为了快速找到缓存中的元素，需要用一个哈希表来存储各个节点的位置。
3.3 代码实现
官方题解代码：
// class LRUCache {
// public:
// LRUCache(int capacity) {
// }
// int get(int key) {
// }
// void put(int key, int value) {
// }
// };
/**
* Your LRUCache object will be instantiated and called as such:
* LRUCache* obj = new LRUCache(capacity);
* int param_1 = obj->get(key);
* obj->put(key,value);
*/
struct DLinkedNode {
int key, value;
DLinkedNode* prev;
DLinkedNode* next;
DLinkedNode(): key(0), value(0), prev(nullptr), next(nullptr) {}
DLinkedNode(int _key, int _value): key(_key), value(_value), prev(nullptr), next(nullptr) {}
};
class LRUCache {
private:
unordered_map<int, DLinkedNode*> cache;
DLinkedNode* head;
DLinkedNode* tail;
int size;
int capacity;
public:
LRUCache(int _capacity): capacity(_capacity), size(0) {
// 使用伪头部和伪尾部节点
head = new DLinkedNode();
tail = new DLinkedNode();
head->next = tail;
tail->prev = head;
}
int get(int key) {
if (!cache.count(key)) {
return -1;
}
// 如果 key 存在，先通过哈希表定位，再移到头部
DLinkedNode* node = cache[key];
moveToHead(node);
return node->value;
}
void put(int key, int value) {
if (!cache.count(key)) {
// 如果 key 不存在，创建一个新的节点
DLinkedNode* node = new DLinkedNode(key, value);
// 添加进哈希表
cache[key] = node;
// 添加至双向链表的头部
addToHead(node);
++size;
if (size > capacity) {
// 如果超出容量，删除双向链表的尾部节点
DLinkedNode* removed = removeTail();
// 删除哈希表中对应的项
cache.erase(removed->key);
// 防止内存泄漏
delete removed;
--size;
}
}
else {
// 如果 key 存在，先通过哈希表定位，再修改 value，并移到头部
DLinkedNode* node = cache[key];
node->value = value;
moveToHead(node);
}
}
void addToHead(DLinkedNode* node) {
node->prev = head;
node->next = head->next;
head->next->prev = node;
head->next = node;
}
void removeNode(DLinkedNode* node) {
node->prev->next = node->next;
node->next->prev = node->prev;
}
void moveToHead(DLinkedNode* node) {
removeNode(node);
addToHead(node);
}
DLinkedNode* removeTail() {
DLinkedNode* node = tail->prev;
removeNode(node);
return node;
}
};
4. 数组中的第K个最大元素【中等】
题目链接：https://leetcode.cn/problems/kth-largest-element-in-an-array/
参考题解：https://leetcode.cn/problems/kth-largest-element-in-an-array/solution/partitionfen-er-zhi-zhi-you-xian-dui-lie-java-dai-/
4.1 题目描述
给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。
请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例1：
输入: [3,2,1,5,6,4], k = 2
输出: 5
示例2：
输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4
提示：
- 1 <= k <= nums.length <= 105
- -104 <= nums[i] <= 104
4.2 解题思路
最简单的思路就是先把数组从小到大排序，返回倒数第 k 个元素即为所求。而根据快速排序每次都会确定一个元素最终位置的这一特点，可以使求解更加快速，即如果当前确定的元素位置恰好就是倒数第 k 个，那么直接返回就可以了。本题的难点是实现快速排序，处理边界情况。
4.3 代码实现
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
srand(time(0));
int n = nums.size();
int target = n - k;
int left = 0;
int right = n - 1;
while (true) {
int pivot = partition(nums, left, right);
if (pivot == target) {
return nums[pivot];
}
else if (pivot < target) {
left = pivot + 1;
}
else {
right = pivot - 1;
}
}
}
int partition(vector<int>& nums, int left, int right) {
int tmp = rand() % (right - left + 1) + left;
swap(nums[tmp], nums[left]);
int pivot = nums[left];
int j = left;
for (int i = left + 1; i <= right; ++i) {
if (nums[i] <= pivot) {
++j;
swap(nums[i], nums[j]);
}
}
swap(nums[left], nums[j]);
return j;
}
};
5. 三数之和【中等】
题目链接：https://leetcode.cn/problems/3sum/
参考题解：https://leetcode.cn/problems/3sum/solution/san-shu-zhi-he-by-leetcode-solution/
5.1 题目描述
给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意： 答案中不可以包含重复的三元组。
示例1：
输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。
示例2：
输入：nums = [0,1,1]
输出：[]
解释：唯一可能的三元组和不为 0 。
示例3：
输入：nums = [0,0,0]
输出：[[0,0,0]]
解释：唯一可能的三元组和为 0 。
提示：
- 3 <= nums.length <= 3000
- -105 <= nums[i] <= 105
5.2 解题思路
首先把数组从小到大排序，这样可以减少循环次数。要满足 a + b + c = 0，如果当前遍历的是 a ，那么只需要判断 b + c 是不是等于 -a 就行了，对于从左往右遍历的每一个 b ，从右往左遍历 c ，这样 b + c 会从大不断变小，直到小于等于 -a ，并且 b 增大的话， c 只能不断变小往左走，否则 b + c 还会变大。所以 b 和 c 可以放到同一个循环中遍历。
5.3 代码实现
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
sort(nums.begin(), nums.end());
int n = nums.size();
vector<vector<int>> ans;
for (int a = 0; a < n; ++a) {
if (a > 0 && nums[a] == nums[a - 1]) {
continue;
}
int target = -nums[a];
int c = n - 1;
for (int b = a + 1; b < n; ++b) {
if (b > a + 1 && nums[b] == nums[b - 1]) {
continue;
}
while (b < c && nums[b] + nums[c] > target) {
--c;
}
if (b == c) {
break;
}
if (nums[a] + nums[b] + nums[c] == 0) {
ans.push_back({nums[a], nums[b], nums[c]});
}
}
}
return ans;
}
};
站长推荐
- U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 - stm32使用HAL库配置串口中断收发数据（保姆级教程）
stm32使用HAL库配置串口中断收发数据（保姆级教程） - SpringSecurity实现前后端分离认证授权
SpringSecurity实现前后端分离认证授权 - 【社区图书馆】伴我前行的一本书《The C Programming Language》
【社区图书馆】伴我前行的一本书《The C Programming Language》 - 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效)