一、用数组模拟邻接表

再上一篇中我们讲了树的两种存储方式：【数据结构与算法】图——邻接表与邻接矩阵
这一篇我们可以用数组来模拟邻接表。
假设现在我们要进行n次操作，实现无向图。
首先需要一个保存是哪个节点的数组e然后就是类似指针数组的表h，每个表都会连一串单链表e,ne

int n;

const int N = 1e5 + 10, M = 2 * N;

int h[N], e[M], ne[M], idx;

void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> n;
    int a, b;
    for(int i = 0; i < n; i++)
    {
        cin >> a >> b;
        add(a, b);
        add(b, a);
    }
    return 0;
}

每次插入其实就是一次头插，这里要注意把h数组初始化成-1，以便标识每个链表的结尾。

二、图的深度优先遍历（dfs）

2.1 概念

我们之前接触过树的遍历，其实树就是一个特殊的图，遍历图的时候我们要注意的是有可能会遍历到我们之前遍历过的点，所以需要一个标志位数组记录遍历过的节点。
给定一个节点u，我们就把这个节点的所有直接相连的点（没有被遍历过的）都进行dfs搜索

void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

void dfs(int u)
{
    cnt[u] = true;
    cout << u << " ";
    for(int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if(!cnt[j])
        {
            dfs(j);
        }
    }
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> n;
    int a, b;
    for(int i = 0; i < n; i++)
    {
        cin >> a >> b;
        add(a, b);
        add(b, a);
    }
    dfs(1);
    return 0;
}

可以看到所有的点都完成了遍历。

2.2 例题：树的重心

题目描述：

给定一颗树，树中包含 n个结点（编号 1∼n）和 n−1条无向边。
请你找到树的重心，并输出将重心删除后，剩余各个连通块中点数的最大值。
重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。

输入格式

第一行包含整数 n，表示树的结点数。接下来 n−1行，每行包含两个整数 a和 b，表示点 a
和点 b之间存在一条边。

输出格式

输出一个整数 m，表示将重心删除后，剩余各个连通块中点数的最大值。

数据范围

1≤n≤105

输入样例

9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6

输出样例：

4

思路分析：
先解释一下这句话：如果将这个点删除后，剩余各个连通块中点数的最大值
举个例子：

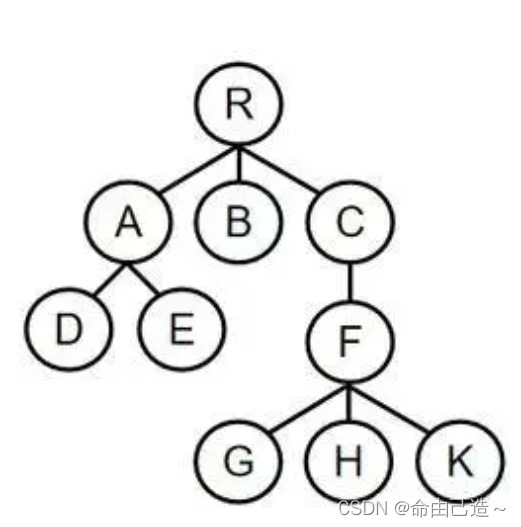
对于点F，把他删除后，会有四个连通块。

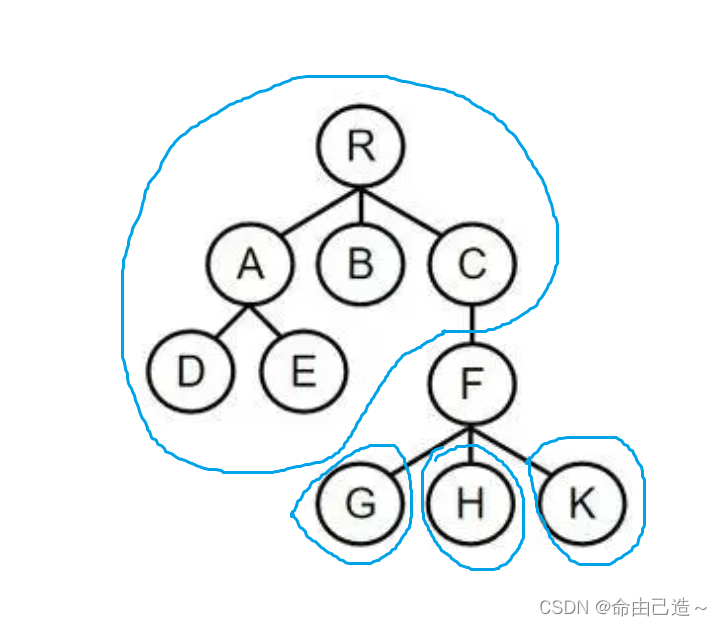
它的最大值就是6。而这个题是要把每个节点的这个最大值求出来，然后取最小值。

那么怎么求呢？

还是以F点举例子，假设现在我们从上面遍历到了F点，下面的几个点好求，但是上面的已经不能再回去了，但是我们知道了一共有多少个节点，我们只需要把下面的节点个数加起来然后再用总数减去即可得到上面有多少个节点，然后取最大值。

#include <iostream>
#include <cstring>

using namespace std;

int n;

const int N = 1e5 + 10, M = 2 * N;
int ans = N;

int h[N], e[M], ne[M], idx;
bool cnt[N];

void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

int dfs(int u)
{
    cnt[u] = true;
    int sum = 1;// 包括当前节点
    int ret = 0;// 记录最大的连通块
    for(int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if(!cnt[j])
        {
            int tmp = dfs(j);
            sum += tmp;
            ret = max(ret, tmp);
        }
    }
    ret = max(ret, n - sum);
    ans = min(ans, ret);
    return sum;
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> n;
    int a, b;
    for(int i = 0; i < n; i++)
    {
        cin >> a >> b;
        add(a, b);
        add(b, a);
    }
    dfs(1);
    cout << ans << endl;
    return 0;
}

三、图的广度优先遍历（bfs）

3.1 概念

我们知道广度优先遍历要借助队列结构，当一个节点入队列后，把所有的相连的点入队列。知道队列为空，还是跟上面一样，防止重复遍历，要加一个标志位。

int n, m;

const int N = 1e5 + 10;

int h[N], e[N], ne[N], idx;
queue<int> q;
bool cnt[N];

void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

void bfs(int u)
{
    cnt[u] = true;
    q.push(u);
    while(q.size())
    {
        int t = q.front();
        q.pop();
        cout << t << " ";
        for(int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if(!cnt[j])
            {
                q.push(j);
                cnt[j] = true;
            }
        }
    }
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> n >> m;
    int a, b;
    while(m--)
    {
        cin >> a >> b;
        add(a, b);
    }
    bfs(1);
    return 0;
}

3.2 例题：图中点的层次

题目描述：

给定一个 n个点 m条边的有向图，图中可能存在重边和自环。所有边的长度都是 1，点的编号为 1∼n。请你求出 1号点到 n号点的最短距离，如果从 1号点无法走到 n号点，输出 −1。

输入格式

第一行包含两个整数 n和 m。
接下来 m行，每行包含两个整数 a和 b，表示存在一条从 a走到 b的长度为 1的边。

输出格式

输出一个整数，表示 1号点到 n号点的最短距离。

数据范围

1≤n,m≤105

输入样例：

4 5
1 2
2 3
3 4
1 3
1 4

输出样例：

1

思路分析：

广度优先遍历的话，第一次遇到n节点的距离一定是最短距离，所以我们这里可以把cnt数组变成d数组，代表每个点离起始位置的距离，先全部初始化成-1，当节点要入队列时，如果距离是-1，说明没有遍历过，那么就入队列，然后改变当前点的距离。

#include <iostream>
#include <cstring>
#include <queue>

using namespace std;

int n, m;

const int N = 1e5 + 10;

int h[N], e[N], ne[N], idx;
queue<int> q;
int d[N];

void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

void bfs(int u)
{
    d[u] = 0;
    q.push(u);
    while(q.size())
    {
        int t = q.front();
        q.pop();
        for(int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if(d[j] == -1)
            {
                q.push(j);
                d[j] = d[t] + 1;
            }
        }
    }
}

int main()
{
    memset(h, -1, sizeof h);
    memset(d, -1, sizeof d);
    cin >> n >> m;
    int a, b;
    while(m--)
    {
        cin >> a >> b;
        add(a, b);
    }
    bfs(1);
    cout << d[n] << endl;
    return 0;
}

四、拓扑排序

4.1 概念

首先要知道什么是拓扑排序：
在一个有向图中，对所有的节点进行排序，要求没有一个节点指向它前面的节点。
先统计所有节点的入度，对于入度为0的节点就可以分离出来，然后把这个节点指向的节点的入度减一。
一直做改操作，直到所有的节点都被分离出来。
如果最后不存在入度为0的节点，那就说明有环，不存在拓扑排序，也就是很多题目的无解的情况。
这里提到了入度的概念，当前点的入度其实就是有多少个节点指向当前节点。
我们以入度为0的节点为突破口，一层一层剥开，如果没有环，则一定能够把所有点的入度减为0。

4.2 例题：有向图的拓扑序列

题目描述：

给定一个 n个点 m条边的有向图，点的编号是 1到 n，图中可能存在重边和自环。
请输出任意一个该有向图的拓扑序列，如果拓扑序列不存在，则输出 −1。
若一个由图中所有点构成的序列 A满足：对于图中的每条边 (x,y)，x在 A中都出现在 y之前，则称 A是该图的一个拓扑序列。

输入格式

第一行包含两个整数 n 和 m。
接下来 m 行，每行包含两个整数 x 和 y，表示存在一条从点 x 到点 y 的有向边 (x,y)。

输出格式

共一行，如果存在拓扑序列，则输出任意一个合法的拓扑序列即可。
否则输出 −1。

数据范围

1≤n,m≤105

输入样例：

3 3
1 2
2 3
1 3

输出样例：

1 2 3

思路分析

这道题我们也是用广度优先遍历的思想，先找到所有入度为0的点，全部入队列，然后一层层的遍历，把入度为0的点剥离，把该节点指向的节点入度减去1，只要入度为0，就入队列，如此循环即可。
然后出队列的元素顺序即为拓扑排序。我们只需要记录入队列的数据个数等不等于总节点个数就可以判断是否是拓扑序列。

#include <iostream>
#include <queue>
#include <cstring>

using namespace std;

const int N = 1e5 + 10;

int h[N], e[N], ne[N], idx;
int in[N];// 入边
queue<int> q;
int res[N];

int n, m, cnt;

void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

void topology()
{
    for(int i = 1; i <= n; i++)
    {
        if(in[i] == 0)
        {
            q.push(i);
        }
    }
    while(q.size())
    {
        int t = q.front();
        q.pop();
        res[cnt++] = t;
        for(int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            in[j]--;
            if(in[j] == 0)
            {
                q.push(j);
            }
        }
    }
}

int main()
{
    memset(h, -1, sizeof(h));
    cin >> n >> m;
    int a, b;
    while(m--)
    {
        cin >> a >> b;
        add(a, b);
        in[b]++;
    }
    
    topology();
    
    if(cnt == n)
    {
        for(int i = 0; i < n; i++)
        {
            cout << res[i] << " ";
        }
    }
    else
    {
        cout << -1;
    }
    return 0;
}