您现在的位置是：首页 >技术杂谈 >算法 DAY57 动态规划13 647. 回文子串 516.最长回文子序列网站首页技术杂谈

647. 回文子串

暴力解法：两层for循环，再加一个判断是否是回文子串，时间复杂度O(n³)
五部曲
1、
判断一个子字符串（字符串的下表范围[i,j]）是否回文，依赖于，子字符串（下表范围[i + 1, j - 1]）） 是否是回文。

所以为了明确这种递归关系，我们的dp数组是要定义成一位二维dp数组。

布尔类型的dp[i][j]：表示区间范围[i,j] （注意是左闭右闭）的子串是否是回文子串，如果是dp[i][j]为true，否则为false。
确定递推公式

2、在确定递推公式

当s[i]与s[j]不相等，，dp[i][j]一定是false。

当s[i]与s[j]相等时，这就复杂一些了，有如下三种情况

情况一：下标i 与 j相同，同一个字符例如a，当然是回文子串
情况二：下标i 与 j相差为1，例如aa，也是回文子串
情况三：下标：i 与 j相差大于1的时候，例如cabac，此时s[i]与s[j]已经相同了，我们看i到j区间是不是回文子串就看aba是不是回文就可以了，那么aba的区间就是 i+1 与 j-1区间，这个区间是不是回文就看dp[i + 1][j - 1]是否为true。

3、初始化
先全部给false

4、遍历顺序
根据dp[i][j]依赖 dp[i + 1][j - 1]
dp[i + 1][j - 1] 在 dp[i][j]的左下角

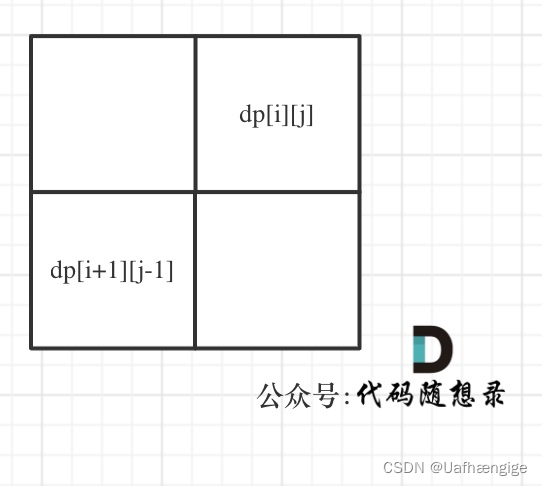
所以一定要从下到上，从左到右遍历，这样保证dp[i + 1][j - 1]都是经过计算的。同时，根据dp的定义，j>=i 是一定的。

class Solution {
public:
    int countSubstrings(string s) {
        vector<vector<bool>> dp(s.size(),vector<bool>(s.size(),false));
        int res = 0;
        for(int i = s.size()-1; i>=0;--i){
            for(int j = i; j<s.size();++j){
                if(s[i] == s[j]){
                    if(j-i<=1) {
                        res++;
                        dp[i][j] = true;
                    }
                    else if(dp[i+1][j-1]){
                        dp[i][j] = true;
                        res++;
                    }
                }
            }
        }
        return res;
    }
};

516.最长回文子序列

回文子串是要连续的，回文子序列可不是连续的！
1、dp
dp[i][j]：字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。
2、递推公式
如果s[i]与s[j]相同，那么dp[i][j] = dp[i + 1][j - 1] + 2;

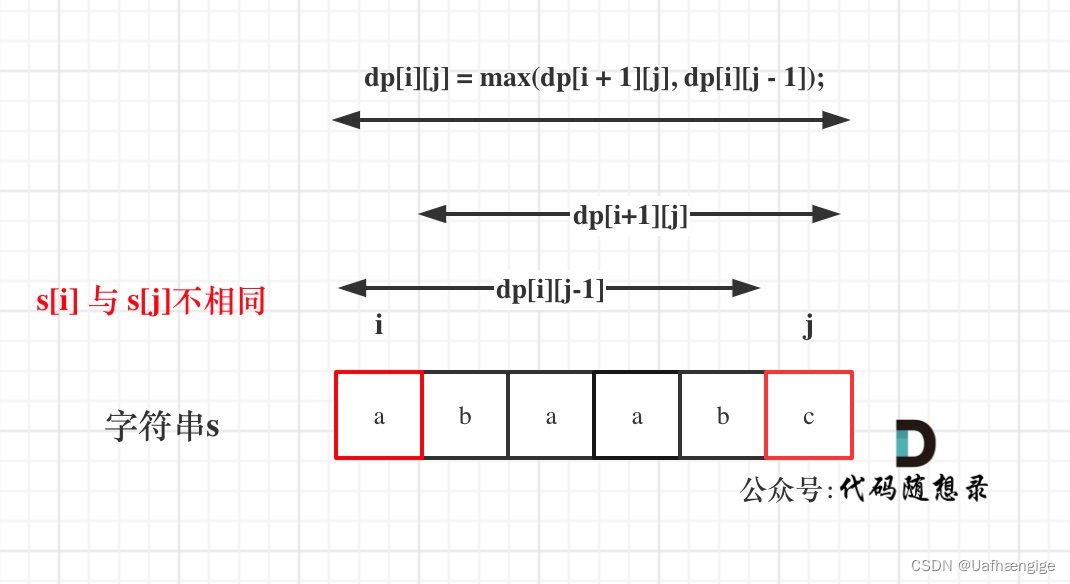
**如果s[i]与s[j]不相同，**说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子序列的长度，那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。

加入s[j]的回文子序列长度为dp[i + 1][j]。
加入s[i]的回文子序列长度为dp[i][j - 1]。

那么dp[i][j]一定是取最大的，即：dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
3、dp数组如何初始化

首先要考虑当i 和j 相同的情况，从递推公式：dp[i][j] = dp[i + 1][j - 1] + 2; 可以看出 递推公式是计算不到 i 和j相同时候的情况。

所以需要手动初始化一下，当i与j相同，那么dp[i][j]一定是等于1的，即：一个字符的回文子序列长度就是1。

放在里面，让j直接从i开始也可以（见版本2代码）

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        vector<vector<int>> dp(s.size(),vector<int>(s.size(),0));
       
       for(int i = 0; i<s.size();++i) dp[i][i] = 1;
        for(int i = s.size()-1;i>=0;--i){
            for(int j = i+1; j<s.size();++j){
                 if(s[i] == s[j]) dp[i][j] = dp[i+1][j-1]+2;
                 else dp[i][j] = max(dp[i+1][j],dp[i][j-1]);
            }
        }
        return dp[0][s.size()-1];
    }
};

版本2：

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        vector<vector<int>> dp(s.size(),vector<int>(s.size(),0));
       
       //for(int i = 0; i<s.size();++i) dp[i][i] = 1;
        for(int i = s.size()-1;i>=0;--i){
            for(int j = i; j<s.size();++j){
                 if(s[i] == s[j]) {
                     if(j-i == 0) dp[i][j] = 1;
                     else if(j-i == 1) dp[i][j] = 2;
                     else dp[i][j] = dp[i+1][j-1]+2;
                 }
                 else dp[i][j] = max(dp[i+1][j],dp[i][j-1]);
            }
        }
        return dp[0][s.size()-1];
    }
};