深入浅出堆—C语言版【数据结构】网站首页 技术杂谈

深入浅出堆—C语言版【数据结构】

小余大牛成长记 2024-06-14 17:18:18

简介深入浅出堆—C语言版【数据结构】

二叉树概念博客：http://t.csdn.cn/XIW84

1. 了解堆

1.1 堆的概念

1.2 堆的性质：

堆中某个节点的值总是不大于或不小于其父节点的值；

堆总是一棵完全二叉树。

1.3 堆的结构图片

1.3.1 小堆

满足下面条件的是小堆

1.3.2 大堆

满足下面条件的是大堆

注意不一定是从大到小、从小到大存储的！！！

堆有什么作用呢？

下面来细讲，别走开！！！

2. 堆的实现

2.1 插入数据进堆

void HeapPush(HP* php, HPDataType x)
{
	assert(php);
	if (php->size == php->capacity)
	{
		int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType)*newcapacity);
		if (tmp == NULL)
		{
			printf("realloc fail
");
			exit(-1);
		}

		php->a = tmp;
		php->capacity = newcapacity;
	}

	php->a[php->size] = x;
	php->size++;

	AdjustUp(php->a, php->size - 1);
}

注意点！！！

假如一开始我们的堆是小堆，但是在插入数据以后要保持还是小堆，要将插入的数据的大小和它的父亲进行比较，比较的两种情况：

1. 如果插入的数据比父亲还要大，那就不需要调整

2. 如果插入的数据比父亲还要小，那就需要调整

如果需要调整，我们就要使用向上调整算法，保持插入数据后的堆还是小堆

2.2 向上调整函数

void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;//求出插入数据的父亲位置下标
	
	while (child > 0)
	{
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;//将父亲的下标给孩子，向上调整
			parent = (child - 1) / 2;//再算出此时插入数据的父亲下标
		}
		else
		{
			break;
		}
	}
}

2.3 堆的删除

能不能使用覆盖删除呢—不能！！！

使用覆盖删除，会打乱父子之间的下标关系，父子关系就会全部乱掉，因此我们使用下面的方法来删除数据

1. 先将下标为0位置的数据和下标最大的数据进行交换

2. 然后直接size--

3. 然后还需要使用向下调整算法，把堆再调整为小堆

void HeapPop(HP* php)
{
	assert(php);
	assert(php->size > 0);

	Swap(&(php->a[0]), &(php->a[php->size - 1]));1.交换
	php->size--;//2. 删除堆顶元素

	AdjustDwon(php->a, php->size, 0);//向下调整，保证还是小堆
}

2.4 向下调整

void AdjustDwon(HPDataType* a, int size, int parent)
{
	int child = parent * 2 + 1;
	while (child < size)
	{
		// 选出左右孩子中小那个
        //这里的if里面的判断大小尽量写成小于是小堆，大于是大堆
		if (child+1 < size && a[child+1] < a[child])
		{
			++child;
		}

		// 孩子跟父亲比较
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}	
}

3. 堆的应用

3.1 建堆（两种方式）

3.1.1 建堆方式1

利用插入元素的方式，向上调整建堆

void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	
	while (child > 0)
	{
		//if (a[child] < a[parent])
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
/

void HeapSort(int* a, int n)//传一个数组过来，还有元素个数
{
	// 建堆方式1：O(N*logN)
	for (int i = 1; i < n; ++i)
	{
		AdjustUp(a, i);//从插入的第二个元素开始
	}
}

建堆方式1的时间复杂度 ——错位相减法

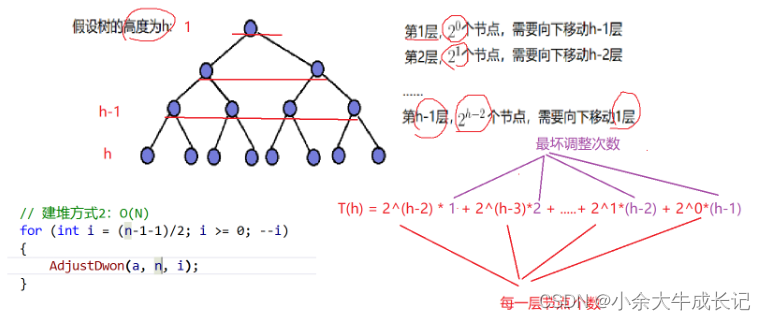
3.1.2 建堆方式2

利用向下调整建堆

方法：找到最后一个元素的父亲，并从这个位置开始向下调整

void HeapSort(int* a, int n)
{

	// 建堆方式2：O(N)
	for (int i = (n-1-1)/2; i >= 0; --i)
	{
		AdjustDwon(a, n, i);
	}

	// O(N*logN)
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDwon(a, end, 0);
		--end;
	}
}

建堆方式2的时间复杂度——错位相减法

3.2 堆排序

排升序，建大堆，再向下调整

为什么建大堆呢？

建大堆，堆顶元素是最大的数，让堆顶元素和最后一个元素交换，再向下调整，注意：这里向下调整时是调整的数组大小-1个，也就是调整刚刚交换下来前面的数据

排降序，建小堆，再向下调整

void HeapSort(int* a, int n)
{

	// 建堆方式2：O(N)
	for (int i = (n-1-1)/2; i >= 0; --i)
	{
		AdjustDwon(a, n, i);
	}

	// O(N*logN)
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);//这里的end是9，传过去向下调整的元素个数也是9，
                             //就不会调整刚刚从堆顶传下来的数据
		AdjustDwon(a, end, 0);
		--end;
	}

3.3 堆的TOP—K问题

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。

比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。

实现思路：

这样空间复杂度非常小

注意：

求前k个最大的数，是建小堆

解释：由于建立的前k个数是小堆，后面n-k个数都可能比对顶的数值大，比堆顶的元素大，就替换堆顶的元素，然后再向下调整，保持前k个数是小堆，然后再比较····

求前k个最小的数，是建大堆（同上）

代码实现：

void PrintTopK(int* a, int n, int k)
{
	// 1. 建堆--用a中前k个元素建堆
	int* kMinHeap = (int*)malloc(sizeof(int)*k);
	assert(kMinHeap);
	for (int i = 0; i < k; ++i)//将a数组里面前10个数赋值给KMinHeap
	{
		kMinHeap[i] = a[i];
	}
	for (int i = (k - 1 - 1) / 2; i >= 0; --i)//向下调整建堆，建立k个数的小堆
	{
		AdjustDwon(kMinHeap, k, i);
	}

	// 2. 将剩余n-k个元素依次与堆顶元素交换，不满则则替换
	for (int j = k; j < n; ++j)
	{
		if (a[j] > kMinHeap[0])
		{
			kMinHeap[0] = a[j];
			AdjustDwon(kMinHeap, k, 0);//再向下调整，保持前k个数是小堆
		}
	}

	for (int i = 0; i < k; ++i)
	{
		printf("%d ", kMinHeap[i]);
	}
	printf("
");
}

void TestTopk()
{    
    //随机生成一万个数字，每个数字%1百万，这一万都是比一百万小的数字，
    //我们将其中的10个数改为比一百万大的值
	int n = 10000;
	int* a = (int*)malloc(sizeof(int)*n);
	srand(time(0));
	for (int i = 0; i < n; ++i)
	{
		a[i] = rand() % 1000000;
	}
	a[5] = 1000000 + 1;
	a[1231] = 1000000 + 2;
	a[531] = 1000000 + 3;
	a[5121] = 1000000 + 4;
	a[120] = 1000000 + 5;
	a[99] = 1000000 + 6;
	a[0] = 1000000 + 7;
	a[76] = 1000000 + 8;
	a[423] = 1000000 + 9;
	a[3144] = 1000000 + 10;

	PrintTopK(a, n, 10);
}