🌻算法，不如说它是一种思考方式🍀

算法专栏： 👉🏻123

一、🌱142. 环形链表 II

• 题目描述：给定一个链表的头节点 head，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。
  如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。
  不允许修改 链表。

• 来源：力扣（LeetCode）

• 难度：中等

• 提示：
  链表中节点的数目范围在范围 [0, 10⁴] 内
  -10⁵ <= Node.val <= 10⁵
  pos 的值为 -1 或者链表中的一个有效索引

• 示例 1：
  
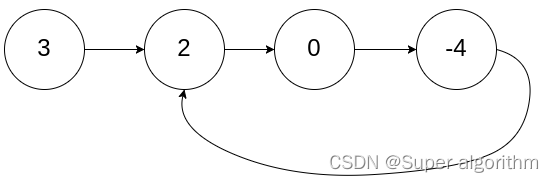
  输入：head = [3,2,0,-4], pos = 1
  输出：返回索引为 1 的链表节点
  解释：链表中有一个环，其尾部连接到第二个节点。
  示例 2：
  输入：head = [1,2], pos = 0
  输出：返回索引为 0 的链表节点
  解释：链表中有一个环，其尾部连接到第一个节点。
  示例 3：
  输入：head = [1], pos = -1
  输出：返回 null
  解释：链表中没有环。

• 进阶：你是否可以使用 O(1) 空间解决此题？

🌴解题

1.HashSet

HashSet是一种不重复的集合。
方法就是遍历链表，判断：集合是否存在这个节点 || 节点为空
 ① 否：存入集合中。
 ② 是：该节点就是所求。

• code：

public class Solution {
    public ListNode detectCycle(ListNode head) {
        Set<ListNode> NodeSet=new HashSet<>();
        ListNode p=head;
        while(!NodeSet.contains(p) && p!=null){//节点判断是否已经被存入（入环首节点），或者 no 环
            NodeSet.add(p);
            p=p.next;
        }
        return p;        
    }
}

2.双指针

定义两个指针：快指针 fast、慢指针 slow。fast 每次走 2 步，slow 每次走 1 步。

1. 相遇
   如果链表有环，那么 fast 和 slow 肯定会相遇；

• 为什么 ？

那么假设环长度是 N；
如果 fast 和slow 可以相遇则有：(a + 2 * k) = (b + k) + r * N ；
即：a + k = b + r * N ；对于这样的方程，取任意a b 可以找到多组解释，
所以 有环则必定相遇。
 

2. 找到入环节点
   对于相遇的节点 fast=slow，我们在取节点 p指向 head，让 p 和 slow 同步遍历，第一次相遇节点为所求节点。

• why ？
  

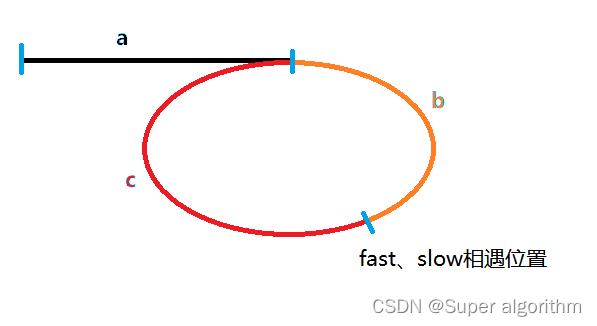
对于fast走到相遇的位置：a + b + n(b + c)；
slow走到相遇的位置：a + b + m(b + c)，其中(m < n)；

而slow每次走的是fast的一半，所以有：2 * [a + b + m(b + c)] = a + b + n(b + c)；
即 a+b = k*(b+c)，
移动变形公式：a = r * (b+c) + c ，其中(r=k-1)；
结合上图看，从 slow 和 head 同步遍历，最后在环的入口相遇。

• code：

public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode fast=head,slow=head;
        while(true){
            if(fast==null||fast.next==null){ //不存在环，fast当然率先 null               
                break;
            }

            fast=fast.next.next;// 2
            slow=slow.next;

            if(fast==slow){// fast、slow 相遇
                fast=head;
                while(fast!=slow){
                    fast=fast.next;
                    slow=slow.next;
                }
                return fast;
            }
        }
        return null;
    }
}

空间复杂度 - O(1)

返回第一页。☝

☕物有本末，事有终始，知所先后。🍭

🍎☝☝☝☝☝我的CSDN☝☝☝☝☝☝🍓