智能算法终极大比拼，以CEC2005测试函数为例，十种智能算法直接打包带走网站首页 学无止境

由于上一篇代码，很多小伙伴留言，说出现了函数安装等运行问题。因此才决定写一篇CEC2005版本的。这个版本的函数无需c++编译器即可使用。

这里说句题外话，函数安装的问题其实在matlab被禁之前，是很好解决的，直接在附加功能添加附件即可。但是被禁之后，安装mingw或者c++编译器，很多刚入门的小伙伴不太会。当然网上有很多教程可以解决，但是咱们的主题是学会智能算法的使用，这里就不再介绍编译器的安装问题啦。

回归正题！CEC2005函数在很多论文中也有提及，毕竟是最经典的国际公认函数测试范例。下面依然是继承上一篇文章的十种智能算法进行测试，没看过这篇文章的小伙伴可以看这里：智能算法终极大比拼，以CEC2017测试函数为例，十种智能算法直接打包带走，不含任何套路！_今天吃饺子的博客-CSDN博客

以CEC2005函数为例，我随意选择了几个函数，每个算法迭代了500次，先上结果图：

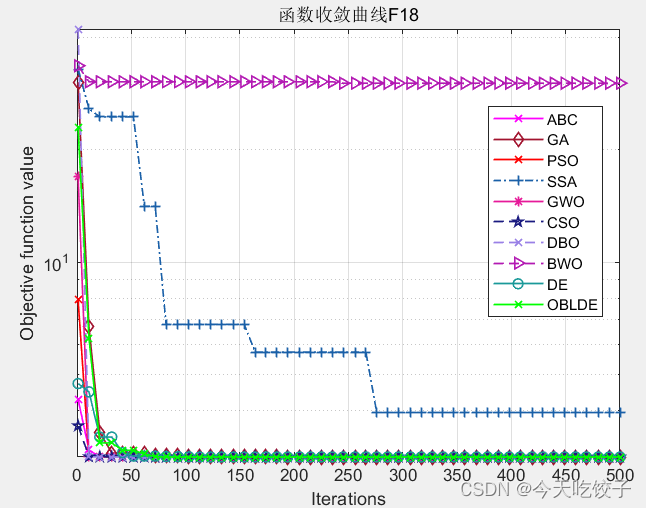
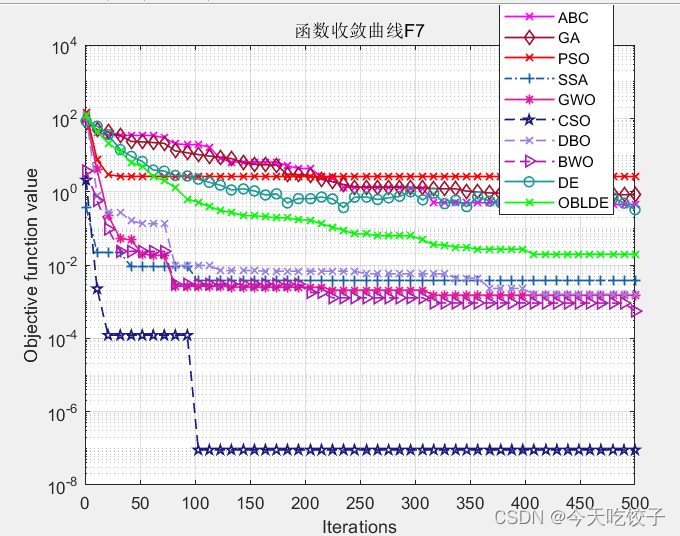
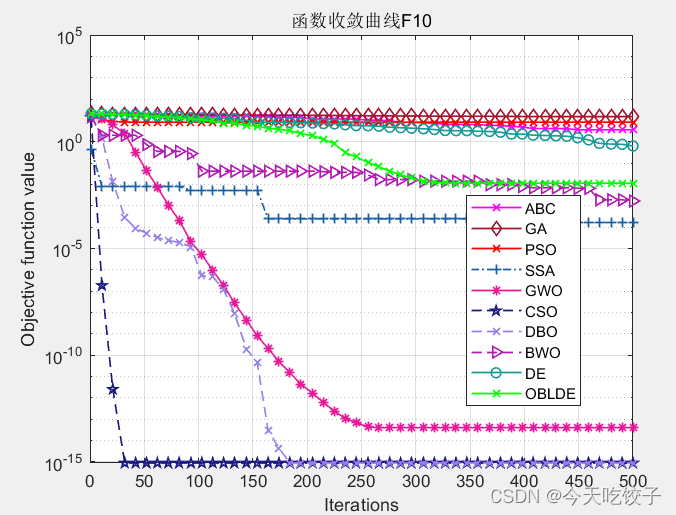
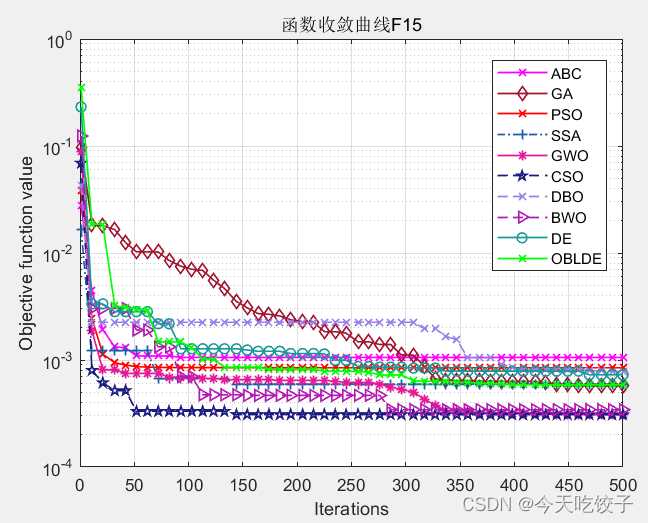
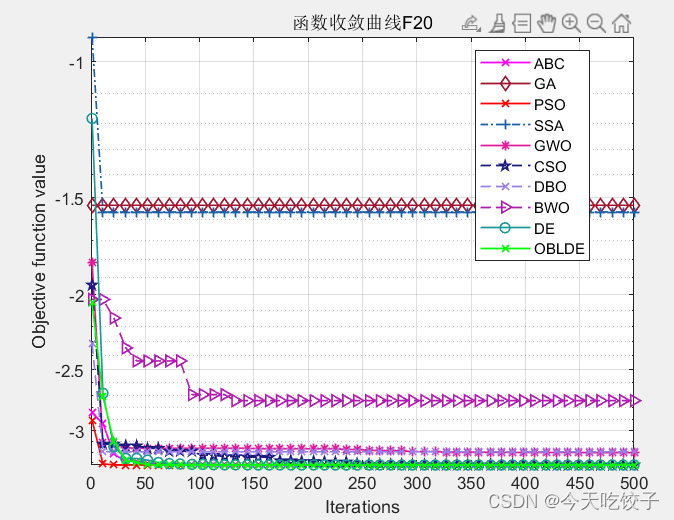
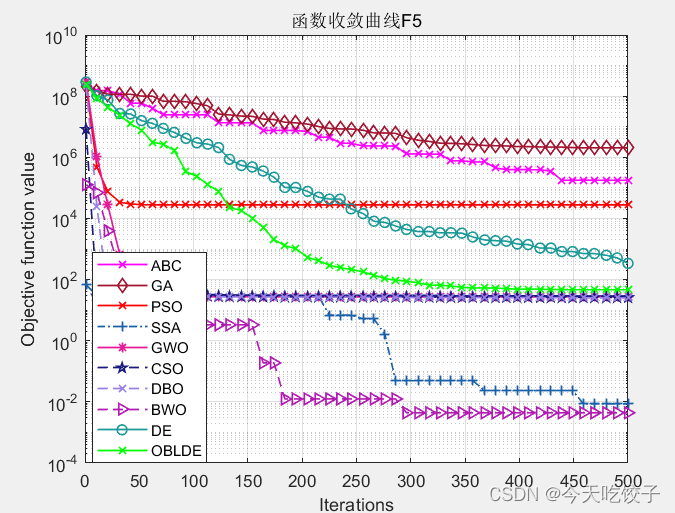
以上几个函数，都是我随机选择的，其他函数我没有一一测试。

接下来到了最关键的上代码阶段！但是，无奈10个算法代码量实在是太大了，这里就截取部分代码啦！

%%
clear
clc
close all
addpath(genpath(pwd));
number='F5'; %选定优化函数，自行替换:F1~F23
% [lb,ub,D,y]：下界、上界、维度、目标函数表达式
[lb,ub,D,y]=CEC2005(number);  

N=50; %种群规模
T=500; %最大迭代次数

%%  各类算法  (N,T,lb,ub,D,y)
[OBLDEfMin,OBLDEbestX,OBLDE_curve]=OBL_impDE(y,N,T,lb,ub,D);   %动态反向学习的DE算法
[DEfMin,DEbestX,DE_curve]=DE(y,N,T,lb,ub,D);      %DE算法
[Alpha_score,Alpha_pos,GWO_curve]=GWO(y,N,T,lb,ub,D);   %灰狼算法
pso_curve=PSO(y,N,T,lb,ub,D);  %粒子群算法
[bestchrom,GA_trace]=ga(y,N,T,lb,ub,D); %遗传算法
ABC_trace = ABC(y,N,T,lb,ub,D);      %人工蜂群
[CSO_Best_score,CSO_Best_pos,cso_trace] = CSO(y,N,T,lb,ub,D);  %鸡群算法
[fMin,bestX,DBO_curve]=DBO(y,N,T,lb,ub,D);       %蜣螂优化
[BWO_Best_pos,BWO_Best_score,BWO_curve] = BWO(y,N,T,lb,ub,D);   %白鲸优化算法
%% 麻雀
%设置SSA算法的参数
Params.nVar=D;                           % 优化变量数目
Params.VarSize=[1 Params.nVar];          % Size of Decision Variables Matrix
Params.VarMin=lb;      % 下限值，分别是a,k
Params.VarMax=ub;        % 上限值
Params.MaxIter=T;       % 最大迭代数目
Params.nPop=N;        % 种群规模
[particle3, GlobalBest3,SD,GlobalWorst3,Predator,Joiner] =  SSAInitialization(y,Params,'SSA');  %初始化SSA参数
[GlobalBest,SSA_curve] =  SSA(y,GlobalBest3,GlobalWorst3,SD,Predator,Joiner,Params);  %采用SSA参数优化VMD的两个参数
%由于麻雀算法是将各个参数放进了一个结构体，这里作者不想再去折腾改了，因此麻雀算法单独设计。

%% 画图
CNT=50;
k=round(linspace(1,T,CNT)); %随机选50个点
% 注意：如果收敛曲线画出来的点很少，随机点很稀疏，说明点取少了，这时应增加取点的数量，100、200、300等，逐渐增加
% 相反，如果收敛曲线上的随机点非常密集，说明点取多了，此时要减少取点数量
iter=1:1:T;
semilogy(iter(k),ABC_trace(k),'m-x','linewidth',1);
hold on
semilogy(iter(k),GA_trace(k),'Color',[0.6350 0.0780 0.1840],'Marker','d','LineStyle','-','linewidth',1);
hold on
semilogy(iter(k),pso_curve(k),'r-x','linewidth',1);
hold on
semilogy(iter(k),SSA_curve(k),'Color',[0.1 0.3780 0.66],'Marker','+','LineStyle','-.','linewidth',1);
hold on
semilogy(iter(k),GWO_curve(k),'Color',[0.9 0.1 0.6],'Marker','*','LineStyle','-','linewidth',1);
hold on
semilogy(iter(k),cso_trace(k),'Color',[0.1 0.1 0.5],'Marker','p','LineStyle','--','linewidth',1);
hold on
semilogy(iter(k),DBO_curve(k),'Color',[0.6 0.5 0.9],'Marker','x','LineStyle','--','linewidth',1);
hold on
semilogy(iter(k),BWO_curve(k),'Color',[0.7 0.1 0.7],'Marker','>','LineStyle','--','linewidth',1);
hold on
semilogy(iter(k),DE_curve(k),'Color',[0.1 0.6 0.6],'Marker','o','LineStyle','-','linewidth',1);
hold on
semilogy(iter(k),OBLDE_curve(k),'g-x','linewidth',1);
grid on;
title(['函数收敛曲线',number])
xlabel('Iterations');
ylabel('Objective function value');
box on
legend('ABC','GA','PSO','SSA','GWO','CSO','DBO','BWO','DE','OBLDE')

DE算法：

function [min_f,min_x,trace]=DE(y,NP,G,c,d,D)

%%%%%%%%%%%%%%%%%%%%%%%%设置参数%%%%%%%%%%%
F = 0.8;%变异算子
CR = 0.1;%交叉算子
Xx= c.*ones(1,D );    % Lower limit/bounds/     a vector
Xs= d.*ones(1,D);    % Upper limit/bounds/     a vector
% Xs = repelem(20,D);%变量取值最大
% Xx = repelem(-20,D);%变量取值最小
yz = 1e-6;%阈值

%%%%%%%%%%%%%%%%%%%%%%%%初始化种群%%%%%%%%%%%
x = zeros(NP,D);%初始种群
v = zeros(NP,D);%变异种群
u = zeros(NP,D);%选择种群
% x = Xx+rand(NP,D)*(Xs-Xx);%赋初值
x=initialization(NP,D,Xs,Xx);
%%%%%%%计算目标函数%%%%%%
Ob = zeros(NP,1);%初始化Ob用来存储种群函数值
for m=1:NP
    Ob(m) = y(x(m,:));

end
trace = zeros(G+1,1);%存储每代种群函数值最小
trace(1) = min(Ob);

%%%%%%%%%%%%%%差分进化循环%%%%%%%%%%%%%
for gen=1:G
    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%变异操作%%%%%%%%%%%%%%%%%%%%%%%%%%%
%     %%%%%%%%%自适应变异算子%%%%%%%%%%%%%%
%     lambda = exp(1-G/(G+1-gen));
%     F = F0*2^lambda;
    %%%%%%%%%r1,r2,r3和m互不相同%%%%%%%%%%%
    for m=1:NP
        r = randperm(NP,3);%在种群中随机选择三个序号作为r1，r2，r3
        r1 = r(1);
        r2 = r(2);
        r3 = r(3);
        v(m,:) = x(r1,:) + F*(x(r2,:)-x(r3,:));
    end
    
    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%交叉操作%%%%%%%%%%%%%%%%%%%%%%%%%%%
    r = randperm(D,1);%随机确定一个维度
    for n=1:D
        cr = rand(1);%产生一个随机数
        if (cr<CR) || (n==r)
            u(:,n) = v(:,n);
        else
            u(:,n) = x(:,n);
        end
    end
    
    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%边界条件的处理%%%%%%%%%%%%%%%%%%%%%%%%%%%
    for n=1:D
        for m=1:NP
            if (u(m,n)<Xx(n)) || (u(m,n)>Xs(n))
                u(m,n) = rand*(Xs(n)-Xx(n))+Xx(n);%超出边界重新赋值
            end
        end
    end
    
    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%选择操作%%%%%%%%%%%%%%%%%%%%%%%%%%%
    Ob1 = zeros(NP,1);
    for m=1:NP
        Ob1(m) = y(u(m,:));

    end
    for m=1:NP
        if Ob1(m)<Ob(m)
            x(m,:) = u(m,:);
        end
    end
    
    %求第G+1代x的值
    for m=1:NP
                Ob(m) =y(x(m,:));

    end
    trace(gen+1) = min(Ob);
%     if min(Ob)<yz
%         break;
%     end
end
[min_f,min_Index] = min(Ob);%找到Ob中最小的值和位置
min_x = x(min_Index,:);%对应最优值的解
end

麻雀优化算法：

function [ GlobalBest,BestCost] =SSA (y,GlobalBest,GlobalWorst,SD,Predator,Joiner,Params)

MaxIter = Params.MaxIter;
nPop = Params.nPop;
VarMin = Params.VarMin;
VarMax = Params.VarMax;
VarSize = Params.VarSize;
nVar=2;%size(VarSize,2);
BestCost = zeros(1,MaxIter);

%% Main loop
for i = 1:MaxIter
    for j = 1:length(Predator)
        alarm =  randn ;
        ST = randn;
        if alarm < ST
            Predator(j).Position = Predator(j).Position .* exp( -j /MaxIter);
        else
            Predator(j).Position = Predator(j).Position + randn * ones(VarSize);
        end
        Predator(j).Position = max(VarMin,Predator(j).Position);
        Predator(j).Position = min(VarMax,Predator(j).Position);

           Predator(j).Cost =y(Predator(j).Position);

      
    end
      [~,idx] = min([Predator.Cost]);
      BestPredator = Predator(idx);
    % 加入者更新
    for j = 1: nPop - length(Predator)
        if j + length(Predator)> nPop/2
            Joiner(j).Position =  randn .* exp( (GlobalWorst.Position - Joiner(j).Position) / j^2);
            
        else
            A = randi([0,1],1,nVar);
            A(~A) = -1;
            Ahat = A' / (A * A');
                Joiner(j).Position = BestPredator.Position + abs(Joiner(j).Position - BestPredator.Position) * Ahat * ones(VarSize);  
        end
        Joiner(j).Position = max(VarMin,Joiner(j).Position);
        Joiner(j).Position = min(VarMax,Joiner(j).Position);
  
        Joiner(j).Cost =y(Joiner(j).Position);

    end
    
    % 警觉者更新
    for j = 1:length(SD)
        if SD(j).Cost > GlobalBest.Cost
            SD(j).Position = GlobalBest.Position + randn * abs( SD(j).Position - GlobalBest.Position);
        
        elseif SD(j).Cost == GlobalBest.Cost
            SD(j).Position = SD(j).Position + (rand*2-1) * (abs( SD(j).Position - GlobalWorst.Position)./ ((SD(j).Cost - GlobalWorst.Cost) + 0.001));
        end
        SD(j).Position = max(VarMin,SD(j).Position);
        SD(j).Position = min(VarMax,SD(j).Position);


    end
  
    
    
% 更新
particle = [Predator;Joiner;SD];
for m = 1:length(particle)
    if GlobalBest.Cost > particle(m).Cost
        GlobalBest = particle(m);
    end
    if GlobalWorst.Cost < particle(m).Cost
        GlobalWorst = particle(m);
    end
end
 
BestCost(i) = GlobalBest.Cost;
 
% disp(['当前迭代',num2str(i), '最优值为: ', num2str(GlobalBest.Cost)])
%    disp(['第',num2str(i),'次寻优的适应度值为：',num2str(BestCost(i))])
%     disp(['第',num2str(i),'次寻优的最佳位置为：[',num2str(GlobalBest.Position),']'])

end

%% Results

% figure;
% %plot(BestCost,'LineWidth',2);
% semilogy(BestCost,'LineWidth',2);
% xlabel('Iteration');
% ylabel('Best Cost');
% grid on;
end

欢迎大家评论区留言哦！

风语者！平时喜欢研究各种技术，目前在从事后端开发工作，热爱生活、热爱工作。

上一篇
C++ Builder XE AdvStringGrid的表格画线...

下一篇
kubernetes和容器安全的7个关键特性...

站长推荐

stm32使用HAL库配置串口中断收发数据（保姆级教程）
stm32使用HAL库配置串口中断收发数据（保姆级教程）
SpringSecurity实现前后端分离认证授权
SpringSecurity实现前后端分离认证授权
U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决
【社区图书馆】伴我前行的一本书《The C Programming Language》
【社区图书馆】伴我前行的一本书《The C Programming Language》
Unity创建文本时自动修改默认字体
Unity创建文本时自动修改默认字体

您现在的位置是：首页 >学无止境 >智能算法终极大比拼，以CEC2005测试函数为例，十种智能算法直接打包带走网站首页学无止境

智能算法终极大比拼，以CEC2005测试函数为例，十种智能算法直接打包带走

上一篇 C++ Builder XE AdvStringGrid的表格画线...

下一篇 kubernetes和容器安全的7个关键特性...

站长推荐

上一篇
C++ Builder XE AdvStringGrid的表格画线...

下一篇
kubernetes和容器安全的7个关键特性...