简单多状态问题

1.按摩师

力扣链接：力扣

一个有名的按摩师会收到源源不断的预约请求，每个预约都可以选择接或不接。在每次预约服务之间要有休息时间，因此她不能接受相邻的预约。给定一个预约请求序列，替按摩师找到最优的预约集合（总预约时间最长），返回总的分钟数。

首先我们分析一下题目：1.每个预约可以选择接或者不接 2.不能接受相邻的预约。

1.状态表示

我们用dp[i]表示i位置的最长分钟数，而i位置又可以分为两种情况，一种是接，一种是不接，所以我们用两个dp表来表示状态。

f[i]表示接i位置的最长分钟数

g[i]表示不接i位置的最长分钟数 

2.状态转移方程

因为f[i]表示接i位置的预约，由于题目要求不能接受相邻的预约，所以我们一定不能接受i-1位置的预约，而g[i-1]就表示不接i-1位置的最长分钟数，又因为我们接了i位置要加上i位置的分钟数，所以

f[i] = g[i-1] + nums[i];

g[i]表示不接i位置，那么我们可以选择接受i-1位置或者不接受i-1位置，又因为我们要的是最大值，所以取这两种情况的较大值即可。

g[i] = max(f[i-1],g[i-1]）

3.初始化

从状态转移方程来看，我们造成越界的位置只有f[0]和g[0]，而f[0]表示接受0位置的最长分钟数，那么f[0] = nums[0]     g[0] = 0.

4.填表

已知f[0]和g[0]所以从左向右依次填表，两个表一起填

5.返回值

因为预约时长都是正数，所以越到后面时间越长，那么最长的只有两种情况：最后一个位置接或者最后一个位置不接，此题要求最大值，所以是这两个情况的较大值。

class Solution {
public:
    int massage(vector<int>& nums) {
       if (nums.size()==0) return 0;
       //创建dp表
       int n = nums.size();
       vector<int> f(n,0),g(n,0);
       f[0] = nums[0],g[0] = 0;
       for (int i = 1;i<n;i++)
       {
           f[i] = g[i-1] + nums[i];
           g[i] = max(f[i-1],g[i-1]);
       }
       return max(f[n-1],g[n-1]);
    }
};

 注意：此题会有nums.size()为0的情况，所以需要单独判断。

2.打家劫舍系列

1.打家劫舍I

力扣链接：力扣

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

 1.状态表示

由于每个位置存在偷与不偷两个状态，所以需要两个表来表示。

f[i]表示偷i位置的最高金额

g[i]表示不偷i位置的最高金额

2.状态转移方程

f[i] = g[i-1] + nums[i];

g[i] = max(f[i-1],g[i-1])

3.初始化，4.填表，5.返回值

与第一题同理。

对于这个题我们应该很熟悉吧，没错！和第一题按摩师简直一模一样，我们直接把按摩师的代码复制过来：

 相同的代码，立马就搞定了，我们将这道题拿出来是为了引出打家劫舍II和III，所以并不是没有用哦~

2.打家劫舍II

力扣链接：力扣

你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警 。

给定一个代表每个房屋存放金额的非负整数数组，计算你 在不触动警报装置的情况下 ，今晚能够偷窃到的最高金额。

注意：和I不同的是，这道题的前后是一个圈，也就是说这是一个环形问题，下面我们来解决这道题。

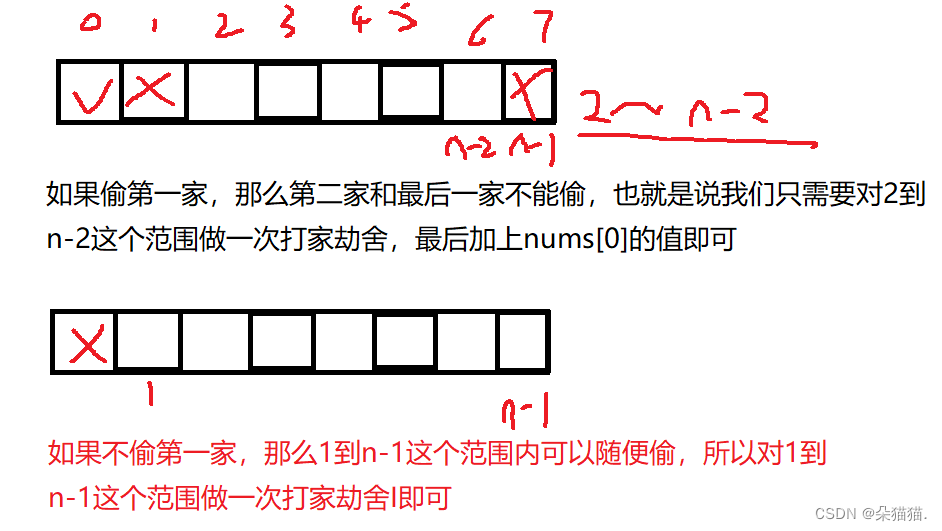
首先我们能将问题分为两种情况，第一种是偷第一家的情况，第二种是不偷第一家的情况。

如果偷第一家，那么第二家和最后一家不能偷，也就是说我们只需要对2到n-2这个范围做一次打家劫舍I，最后加上nums【0】即可。

如果不偷第一家，那么1到n-1这个范围内可以随便偷，所以对1到n-1这个范围内做一次打家劫舍I即可。

class Solution {
public:
    int rob(vector<int>& nums) {
       int n = nums.size();
       return max(nums[0]+rob1(nums,2,n-2),rob1(nums,1,n-1));
    }
    int rob1(vector<int>& nums,int left,int right)
    {
        if (left>right) return 0;
        int n = nums.size();
        vector<int> f(n, 0), g(n, 0);
        f[left] = nums[left], g[left] = 0;
        for (int i = left+1; i <= right; i++)
        {
            f[i] = g[i - 1] + nums[i];
            g[i] = max(f[i - 1], g[i - 1]);
        }
        return max(f[right], g[right]);
    }
};

 注意：当我们left大于right的时候那么一定是越界的情况，这种情况返回0即可。当我们将区间定为left到right这个闭区间，那么就从left+1开始填表，填到right，最后返回的时候也是返回dp表中right的位置，这里一定要画图映射位置关系。

3.删除并获得点数

力扣链接：力扣

给你一个整数数组 nums ，你可以对它进行一些操作。

每次操作中，选择任意一个 nums[i] ，删除它并获得 nums[i] 的点数。之后，你必须删除 所有 等于 nums[i] - 1 和 nums[i] + 1 的元素。

开始你拥有 0 个点数。返回你能通过这些操作获得的最大点数。

 首先通过题目我们可以看到当我们删除X获取X的点数后，必须删除X-1和X+1的元素，我们发现这与打家劫舍的问题非常像，都是不能获得相邻元素的值，那么我们该如何将这个问题转化为打家劫舍问题呢？其实很简单，因为X-1 和 X 和 X+1这三个数都是相邻的，我们直接将nums映射到一个与下标同值的表中，比如3就放在下标为3的位置，并且给这个位置加上3，然后我们对这个新数组做一次打家劫舍就得到了最大点数。

比如实例2，映射后变成如下图：

然后我们对这个数组做一次打家劫舍，获取的最大点数就是9.

class Solution {
public:
    int deleteAndEarn(vector<int>& nums) {
        int hash[10001] = {0};
        const int n = 10001;
        for (auto& a:nums)
        {
            hash[a]+=a;
        }
        vector<int> f(n, 0), g(n, 0);
        for (int i = 1; i < n; i++)
        {
            f[i] = g[i - 1] + hash[i];
            g[i] = max(f[i - 1], g[i - 1]);
        }
        return max(f[n-1], g[n-1]);
    }
};

 此方法就是用空间换时间。

4.粉刷房子

力扣链接：力扣

假如有一排房子，共 n 个，每个房子可以被粉刷成红色、蓝色或者绿色这三种颜色中的一种，你需要粉刷所有的房子并且使其相邻的两个房子颜色不能相同。

当然，因为市场上不同颜色油漆的价格不同，所以房子粉刷成不同颜色的花费成本也是不同的。每个房子粉刷成不同颜色的花费是以一个 n x 3 的正整数矩阵 costs 来表示的。

例如，costs[0][0] 表示第 0 号房子粉刷成红色的成本花费；costs[1][2] 表示第 1 号房子粉刷成绿色的花费，以此类推。

请计算出粉刷完所有房子最少的花费成本。

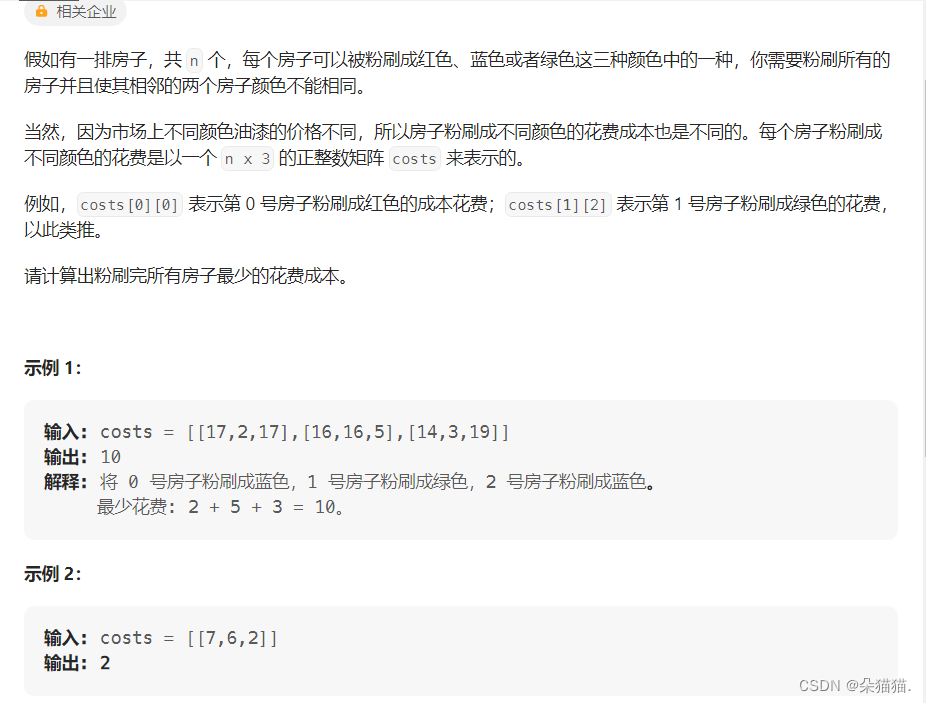
 首先我们通过题目可以知道限制条件为：相邻房屋不能涂成同一个颜色，下面我们开始解题。

1.状态表示

dp【i】表示第i个房子所花费的最低成本，由于每个房子都可以涂成三种颜色，所以dp[i]又可以划分成3个状态。

dp[i][0]表示第i个房子涂成红色的最低成本

dp[i][1]表示第i个房子涂成蓝色的最低成本

dp[i][2]表示第i个房子涂成绿色的最低成本

2.状态转移方程

dp[i][0] = min(dp[i-1][1],dp[i-1][2]) + costs[i][0];

dp[i][1] = min(dp[i-1][0],dp[i-1][2]) + costs[i][1];

dp[i][2] = min(dp[i-1][0],dp[i-1][1]) + costs[i][2];

由于每个房子不能涂成相同颜色，所以第i层的房子如果是红色，那么第i-1层就只能是蓝色和绿色。

3.初始化

由于第一个房子不受前面任何房子的影响（i-1越界），所以第一个房子的三个状态都是已知的

dp[0][0] = costs[0][0],

dp[0][1] = costs[0][1],

dp[0][2] = costs[0][2];

4.填表

从左向右依次填表，三个表一起填

5.返回值

返回最后一个房子的三种状态的最小值。

class Solution {
public:
    int minCost(vector<vector<int>>& costs) {
       int n = costs.size();
       vector<vector<int>> dp(n,vector<int>(3));
       dp[0][0] = costs[0][0],dp[0][1] = costs[0][1],dp[0][2] = costs[0][2];
       for (int i = 1;i<n;i++)
       {
           dp[i][0] = min(dp[i-1][1],dp[i-1][2]) + costs[i][0];
           dp[i][1] = min(dp[i-1][0],dp[i-1][2]) + costs[i][1];
           dp[i][2] = min(dp[i-1][0],dp[i-1][1]) + costs[i][2];
       }
       int ret = dp[n-1][0];
       for (int i =1;i<3;i++)
       {
           if (dp[n-1][i]<ret)
           {
               ret = dp[n-1][i];
           }
       }
       return ret;
    }
};

当然我们也可以将最后取最小值的代码简化一下：

class Solution {
public:
    int minCost(vector<vector<int>>& costs) {
       int n = costs.size();
       vector<vector<int>> dp(n,vector<int>(3));
       dp[0][0] = costs[0][0],dp[0][1] = costs[0][1],dp[0][2] = costs[0][2];
       for (int i = 1;i<n;i++)
       {
           dp[i][0] = min(dp[i-1][1],dp[i-1][2]) + costs[i][0];
           dp[i][1] = min(dp[i-1][0],dp[i-1][2]) + costs[i][1];
           dp[i][2] = min(dp[i-1][0],dp[i-1][1]) + costs[i][2];
       }
       int ret = min(dp[n-1][0],min(dp[n-1][1],dp[n-1][2]));
       return ret;
    }
};

以上就是本篇文章的5道动态规划习题，还是建议大家在做动态规划习题的时候要多画图。