LeetCode 2352. Equal Row and Column Pairs【模拟,哈希表,前缀树】中等网站首页 技术交流

LeetCode 2352. Equal Row and Column Pairs【模拟,哈希表,前缀树】中等

memcpy0 2024-09-14 00:01:02

简介LeetCode 2352. Equal Row and Column Pairs【模拟,哈希表,前缀树】中等

本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库：https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

给你一个下标从 0 开始、大小为 n x n 的整数矩阵 grid ，返回满足 Ri 行和 Cj 列相等的行列对 (Ri, Cj) 的数目。

如果行和列以相同的顺序包含相同的元素（即相等的数组），则认为二者是相等的。

示例 1：

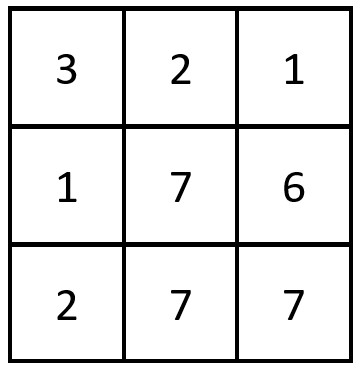
输入：grid = [[3,2,1],[1,7,6],[2,7,7]]
输出：1
解释：存在一对相等行列对：
- (第 2 行，第 1 列)：[2,7,7]

示例 2：

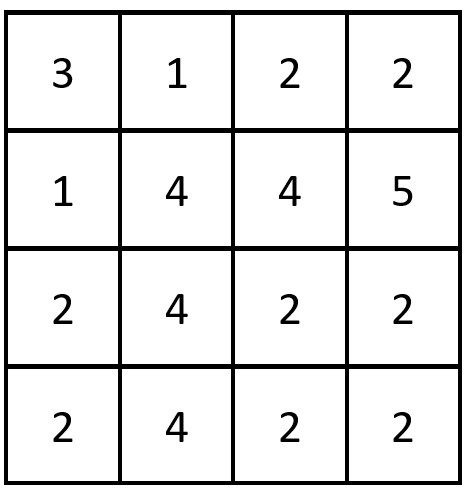
输入：grid = [[3,1,2,2],[1,4,4,5],[2,4,2,2],[2,4,2,2]]
输出：3
解释：存在三对相等行列对：
- (第 0 行，第 0 列)：[3,1,2,2]
- (第 2 行, 第 2 列)：[2,4,2,2]
- (第 3 行, 第 2 列)：[2,4,2,2]

提示：

n == grid.length == grid[i].length
1 <= n <= 200
1 <= grid[i][j] <= 10^5

解法1 模拟

按照题目要求对任意一行，将它与每一列都进行比较，如果相等则结果加一，最后返回总数。

class Solution {
public:
    int equalPairs(vector<vector<int>>& grid) {
        int n = grid.size();
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) { // 每次将第i行比较第j列
                int ok = 1;
                for (int k = 0; k < n; ++k) {
                    if (grid[i][k] != grid[k][j]) { // 第i行第k列等于第j列第k行
                        ok = 0;
                        break;
                    }
                }
                ans += ok;
            }
        }
        return ans;
    }
};

复杂度分析：

时间复杂度： $O(n^3)$
空间复杂度： $O (1)$

解法2 哈希表

首先将矩阵的行放入哈希表中统计次数，哈希表的键可以是将行（用分隔符）拼接后的字符串，也可以用各语言内置的数据结构，然后分别统计与每一列相等的行有多少，求和即可。

class Solution {
    public int equalPairs(int[][] grid) {
        int n = grid.length;
        var cnt = new HashMap<List<Integer>, Integer>();
        for (int[] row : grid) {
            List<Integer> arr = new ArrayList<Integer>();
            for (int num : row) arr.add(num);
            cnt.put(arr, cnt.getOrDefault(arr, 0) + 1);
        }
        int ans = 0;
        for (int j = 0; j < n; ++j) {
            var arr = new ArrayList<Integer>();
            for (int i = 0; i < n; ++i) arr.add(grid[i][j]);
            ans += cnt.getOrDefault(arr, 0);
        }
        return ans;
    }
}

复杂度分析：

时间复杂度： $O(n^2)$ ，将行放入哈希表中消耗 $O(n^2)$ ，读取所有列的哈希表中的次数也消耗 $O(n^2)$
空间复杂度： $O(n^2)$ ，哈希表的空间复杂度为 $O(n^2)$

解法3 前缀树

将每行当成一个数值序列，存到前缀树中；然后对每一列，分别查询其在前缀树中相同的数值序列个数。

class Solution {
private:
    class Trie {
    public: 
        int endNum; // 记录以此为终结点的数组的个数
        Trie() : endNum(0) {}
        unordered_map<int, Trie*> children;    
    };
public:
    int equalPairs(vector<vector<int>>& grid) {
        int n = grid.size();
        Trie* root = new Trie;
        Trie* cur = root;
        for (int i = 0; i < n; ++i) {
            cur = root;
            for (int j = 0; j < n; ++j) {
                if (!cur->children[grid[i][j]])
                    cur->children[grid[i][j]] = new Trie;
                cur = cur->children[grid[i][j]];
            }
            ++cur->endNum;
        }
        int ans = 0;
        for (int j = 0; j < n; ++j) {
            cur = root;
            for (int i = 0; i < n; ++i) {
                if (cur->children[grid[i][j]])
                    cur = cur->children[grid[i][j]];
                else break;
            }
            ans += cur->endNum;
        }
        return ans;
    }
};