您现在的位置是：首页 >学无止境 >PyTorch深度学习实战（2）——PyTorch张量及其操作网站首页学无止境

0. 前言

PyTorch 是广泛应用于机器学习领域中的强大开源框架，因其易用性和高效性备受青睐。在本节中，将介绍使用 PyTorch 构建神经网络的基础知识。首先了解 PyTorch 的核心数据类型——张量对象。然后，我们将深入研究用于张量对象的各种操作。PyTorch 提供了许多帮助构建神经网络的高级方法及组件，并提供了利用 GPU 更快地训练神经网络的张量对象。

1. 搭建 PyTorch 环境

关于 Python 的安装和配置，在此不再赘述。由于深度学习中模型的训练需要大量时间，因此通常使用 GPU加速计算，在安装 PyTorch 之前需要根据选用的 PyTorch 版本和显卡安装 CUDA 和 cudnn，关于 CUDA 和 cudnn 的安装和配置可以参考官方文档，建议在安装之前根据自己的操作系统认真查看官方的安装文档，可以避免踩不必要的坑。如果计算机中含有 NVIDIA 显卡作为硬件组件，建议安装 CUDA 驱动程序，该驱动程序可将深度学习训练速度提高几个数量级。
然后，在 PyTorch 官方网页，根据自己实际的环境，进行相应的选择，在 Run this Command 栏中将给出安装 PyTorch 的命令：

在此，我们以 Linux、pip、Python 和 CUDA10.2 为例，复制并在终端执行安装命令：

pip3 install torch torchvision torchaudio

为了确认 PyTorch 已正确安装，可以在 Python shell 中运行以下代码：

>>> import torch
>>> test = torch.empty(2,2)
>>> print(test)
tensor([[2.9685e-26, 4.5722e-41],
        [2.9685e-26, 4.5722e-41]])

如果能够正确调用 PyTorch 相关函数，表明 PyTorch 已正确安装。需要注意的是，以上代码中，使用 torch.emty() 中创建了一个尺寸为 2 x 2 的张量，它是一个空矩阵，这里的“空”并不意味着所有元素的值都为 Null，而是使用一些被认为是占位符的无意义浮点数，需要在之后进行赋值，这与 NumPy 中的空数组类似。

2. PyTorch 张量

张量 (Tensors) 是 PyTorch 的基本数据类型，张量是类似于 NumPy 中的多维矩阵 ndarrays：

• 标量可以表示为零维张量
• 向量可以表示为一维张量
• 二维矩阵可以表示为二维张量
• 多维矩阵可以表示为多维张量

张量表示如下图所示：

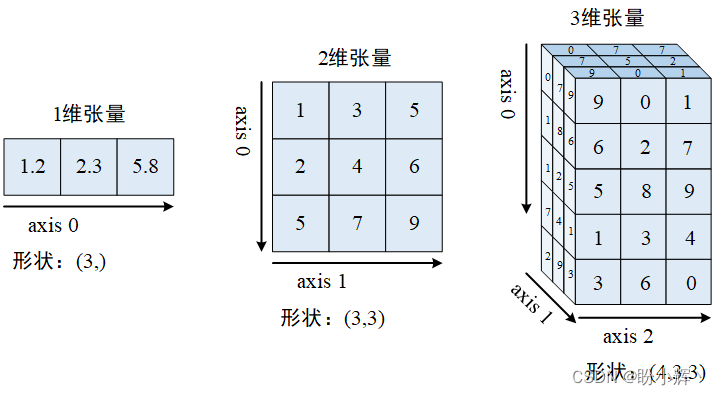
例如，我们可以将彩色图像视为像素值的三维张量，因为彩色图像由 h x w x 3 个像素组成，其中，h 和 w 分别表示图像的高和宽，三个通道对应于 RGB 通道。类似地，灰度图像可以表示为 2 维张量，因为它由 h x w 个像素组成。

2.1 张量初始化

张量除了可以用作图像的基本数据结构外，另一种常见用途是利用张量来初始化连接神经网络不同层的权重。在本节中，我们将学习初始化张量对象的不同方法。

(1) 导入 PyTorch 并通过在列表上调用 torch.tensor 来初始化张量：

import torch
x = torch.tensor([[1,2]])
y = torch.tensor([[1],[2]])

(2) 获取张量对象的形状和数据类型：

print(x.shape)
# torch.Size([1,2]) # one entity of two items
print(y.shape)
# torch.Size([2,1]) # two entities of one item each
print(x.dtype)
# torch.int64

同一张量中的所有元素的数据类型相同，这意味着如果张量包含不同数据类型的数据(例如布尔、整数和浮点数)，则整个张量将被强制转换为最通用的数据类型：

x = torch.tensor([False, 1, 2.0])
print(x)
# tensor([0., 1., 2.])

在以上输出结果中可以看到，布尔值 False 和整数 1 被转换为浮点数。
类似于 NumPy，我们也可以使用内置函数初始化张量对象，以便用于神经网络的权重初始化。

(3) 生成一个 3 行 4 列用 0 填充的张量对象：

a = torch.zeros((3, 4))
print(a)
"""
tensor([[0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.]])
"""

(4) 生成一个 3 行 4 列用 1填充的张量对象：

b = torch.ones((3, 4))
print(b)
"""
tensor([[1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.]])
"""

(5) 生成 3 行 4 列的张量对象，其中每个元素为 0 到 10 之间的随机整数值：

c = torch.randint(low=0, high=10, size=(3,4))
print(c)
"""
tensor([[8, 5, 5, 5],
        [1, 5, 4, 5],
        [6, 2, 9, 4]])
"""

(6) 生成 3 行 4 列的张量对象，其中每个元素为 0 到 1 之间的随机浮点值：

d = torch.rand(3, 4)
print(d)
"""
tensor([[0.4568, 0.8829, 0.8788, 0.2159],
        [0.8409, 0.9374, 0.6409, 0.2946],
        [0.7399, 0.4378, 0.8857, 0.2846]])
"""

(7) 生成 3 行 4 列的张量对象，其中每个元素服从正态分布：

e = torch.randn((3,4))
print(e)
"""
tensor([[ 0.3995,  1.1180, -0.0466,  0.9838],
        [-0.2359,  0.8302, -0.1792, -1.5365],
        [ 0.0842,  0.5544,  0.9606, -1.0090]])
"""

(8) 也可以使用 torch.tensor(<numpy-array>) 直接将 NumPy 数组转换为 Torch 张量：

import numpy as np
x = np.array([[10,20,30],[2,3,4]])
y = torch.tensor(x)
print(type(x), type(y))
# <class 'numpy.ndarray'> <class 'torch.Tensor'>

2.2 张量运算

与 NumPy 类似，张量对象同样可以执行各种基本运算，神经网络中的常见运算包括输入与权重的矩阵相乘、添加偏置项、以及在需要时整形 (reshape) 输入或权重值。

(1) 将 x 中所有元素乘以 10：

import torch
x = torch.tensor([[1,2,3,4], [5,6,7,8]]) 
print(x * 10)
"""
tensor([[10, 20, 30, 40],
[50, 60, 70, 80]])
"""

(2) 将 x 中所有元素增加 10，并将结果张量存储在 y 中：

x = torch.tensor([[1,2,3,4], [5,6,7,8]]) 
y = x.add(10)
print(y)
"""
tensor([[11, 12, 13, 14],
[15, 16, 17, 18]])
"""

(3) 使用 view() 方法对张量进行整形：

y = torch.tensor([2, 3, 1, 0]) # y.shape == (4)
y = y.view(4,1)                # y.shape == (4, 1)

整形张量的另一种方法是使用 squeeze 方法，需要提供要删除的轴索引，需要注意的是，这仅适用于要删除的轴在该维度中只有一项时：

x = torch.randn(10,1,10)
z1 = torch.squeeze(x, 1) 
z2 = x.squeeze(1)
assert torch.all(z1 == z2) 
print('Squeeze:
', x.shape, z1.shape)
"""
Squeeze:
torch.Size([10, 1, 10]) torch.Size([10, 10])
"""

(4) 与 squeeze 相反的操作是 unsqueeze，即向矩阵添加一个新维度：

x = torch.randn(10,10)
print(x.shape)
# torch.size(10,10)
z1 = x.unsqueeze(0)
print(z1.shape)
# torch.size(1,10,10)
x = torch.randn(10,10)
z2, z3, z4 = x[None], x[:,None], x[:,:,None]
print(z2.shape, z3.shape, z4.shape)
# torch.Size([1, 10, 10]) torch.Size([10, 1, 10]) torch.Size([10, 10, 1])

使用 None 进行索引是一种重要的解压方式，通常用于创建新通道/维度。

(5) 执行两个不同张量的矩阵乘法：

x = torch.tensor([[1,2,3,4], [5,6,7,8]])
print(torch.matmul(x, y))
'''
tensor([[11],
        [35]])
'''

矩阵乘法也可以通过使用 @ 运算符来执行：

print(x@y)
'''
tensor([[11],
        [35]])
'''

(6) 与 NumPy 中的连接操作 (concatenate) 类似，可以使用 cat 方法执行张量连接：

import torch
x = torch.randn(10,10,10)
z = torch.cat([x,x], axis=0) # np.concatenate()
print('Cat axis 0:', x.shape, z.shape)
# Cat axis 0:  torch.Size([10, 10, 10]) torch.Size([20, 10, 10])
z = torch.cat([x,x], axis=1) # np.concatenate()
print('Cat axis 1:', x.shape, z.shape)
# Cat axis 1: torch.Size([10, 10, 10]) torch.Size([10, 20, 10])

(7) 提取张量中最大值：

x = torch.arange(25).reshape(5,5)
print('Max:', x.shape, x.max()) 
# Max: torch.Size([5, 5]) tensor(24)

提取最大值以及存在最大值的行索引：

x.max(dim=0)
'''
torch.return_types.max(
values=tensor([20, 21, 22, 23, 24]),
indices=tensor([4, 4, 4, 4, 4]))
'''

需要注意的是，在以上输出中，我们获得了维度 0 上的最大值，这在此张量中表示行。因此，所有行的最大值是第 4 个索引中存在的值，因此索引输出也是 4。此外，max() 方法可以返回最大值和最大值的位置 (argmax)。

类似的，跨列取最大值时的输出如下：

m, argm = x.max(dim=1) 
print('Max in axis 1:
', m, argm) 
'''
Max in axis 1:
 tensor([ 4,  9, 14, 19, 24]) tensor([4, 4, 4, 4, 4])
'''

min 操作与 max 完全相同，其返回最小值和最小值的位置 (argmin)。

(8) 重排 (permute) 张量对象的维度，当我们在原始张量之上执行 permute 时，张量的形状会发生变化：

x = torch.randn(10,20,30)
z = x.permute(2,0,1) # np.permute()
print('Permute dimensions:', x.shape, z.shape)
# Permute dimensions: torch.Size([10, 20, 30]) torch.Size([30, 10, 20])

避免使用 tensor.view 张量交换对象维度，即使 PyTorch 不会抛出错误，但这会在训练期间产生无法预料的结果，如果需要交换维度，推荐使用 permute。

基本上，我们可以在 PyTorch 中使用与 NumPy 几乎相同的语法来执行几乎所有 NumPy 标准数学运算，例如 abs、add、argsort、ceil、floor、sin、cos、tan、cumsum、cumprod、diag、eig、exp、log、log2、log10、mean、median、mode、resize、round、sigmoid、softmax、square、sqrt、svd 和 transpose 等。可以使用 dir(torch.Tensor) 查看 PyTorch 张量的所有可用方法，使用 help(torch.Tensor.<method>) 可以查看该方法的官方帮助文档。

dir(torch.Tensor)
'''
['T',
 '__abs__',
 '__add__',
 '__and__',
 '__array__',
 '__array_priority__',
 '__array_wrap__',
 '__bool__',
 ...
]
'''

help(torch.Tensor.view)
'''
Help on method_descriptor:

view(...)
    view(*shape) -> Tensor
    
    Returns a new tensor with the same data as the :attr:`self` tensor but of a
    different :attr:`shape`.
    ...
'''

2.3 张量对象的自动梯度计算

微分和计算梯度在更新神经网络的权重中起着至关重要的作用，PyTorch 的张量对象内置梯度计算函数。在本节中，我们将了解如何使用 PyTorch 计算张量对象的梯度。

(1) 定义一个张量对象，同时指定它需要计算梯度：

import numpy as np
import torch
x = torch.tensor([[2., -1.], [1., 1.]], requires_grad=True)
print(x)
'''
tensor([[ 2., -1.],
        [ 1.,  1.]], requires_grad=True)
'''

在以上代码中， requires_grad 参数指定要为张量对象计算梯度。

(2) 定义计算输出的方法，计算所有输入的平方和：

out = x.pow(2).sum()

我们知道以上函数的梯度是 2*x，使用 PyTorch 提供的内置函数进行验证。

(3) 通过对该值调用 backward() 方法来计算该值的梯度：

out.backward()

(4) 计算得到 out 关于 x 的梯度，如下所示：

print(x.grad)

输出结果如下所示：

'''
tensor([[ 4., -2.],
        [ 2.,  2.]])
'''

获得的梯度与数学上的梯度值（2*x）相匹配。到目前为止，我们已经了解了在张量对象的初始化、基本运算和梯度计算——它们共同构成了神经网络的基本组件。

3. PyTorch 张量相对于 NumPy 数组的优势

在计算最佳权重值时，会对每个权重进行微量修改，并观察它对降低损失值的影响。需要注意的是，一个权重更新的损失计算不影响同一迭代中其他权重更新的损失计算。因此，每个权重更新可以由不同的核心并行进行，而非顺序更新权重，在这种情况下，GPU 与 CPU 相比更具优势，因为 GPU 通常包含数千个核心。
与 NumPy 相比，PyTorch 张量对象经过优化以配合 GPU 使用。接下来，我们比较使用 NumPy 数组 (ndarray) 和 Tensor 张量 (tensor) 执行矩阵乘法所花费的时间。

(1) 生成两个不同的 torch 对象：

import torch
import time
x = torch.rand(1, 6400)
y = torch.rand(6400, 5000)

(2) 定义用于存储张量对象的设备：

device = 'cuda' if torch.cuda.is_available() else 'cpu'
assert device == 'cuda', "This exercise is on a GPU machine"

(3) 将步骤 1 中创建的张量对象注册到设备中，注册张量对象意味着将信息存储在指定设备中：

x, y = x.to(device), y.to(device)

(4) 执行 Torch 对象的矩阵乘法，并对其计时，并比较在 NumPy 数组上执行矩阵乘法的速度：

start = time.time()
for i in range(100):
    z=(x@y)
end = time.time()
print('Computation with GPU: ', format((end-start)/100, '.8f'))
# Computation with GPU:  0.00001792

(5) 在 cpu 上执行相同的张量矩阵乘法：

x, y = x.cpu(), y.cpu()
start = time.time()
for i in range(100):
    z=(x@y)
end = time.time()
print('Computation with CPU: ', format((end-start)/100, '.8f'))
# Computation with CPU:  0.00665767

(6) 在 NumPy 数组上执行相同的矩阵乘法：

import numpy as np
x = np.random.random((1, 6400))
y = np.random.random((6400, 5000))
start = time.time()
for i in range(100):
    z = np.matmul(x,y)
end = time.time()
print('Computation with NumPy: ', format((end-start)/100, '.8f'))
# Computation with NumPy:  0.01121808

在 GPU 上对 Torch 对象执行的矩阵乘法比在 CPU 上的 Torch 对象快约 18 倍，比在 NumPy 数组上执行矩阵乘法快约 40 倍。一般来说，在 CPU 上使用 Torch 张量的矩阵乘法同样比 NumPy 更快。

小结

在本节中，我们学习了如何使用 PyTorch 的张量对象实现神经网络的基本组件，包括张量对象的初始化 (torch.tensor)、基本运算 (view、max、min、和 squeeze 等) 和梯度计算 (通过 requires_grad 参数指定要为张量对象计算梯度)，并且对比了 PyTorch 张量相对于 NumPy 数组的优势。

系列链接

PyTorch深度学习实战（1）——神经网络与模型训练过程详解