您现在的位置是：首页 >其他 >【数据结构】二叉搜索树网站首页其他

【数据结构】二叉搜索树

冧轩在努力 2024-06-21 18:01:02
简介【数据结构】二叉搜索树

目录

一、二叉搜索树

⭐1.1 二叉搜索树的概念

⭐1.2 二叉搜索树具有的性质：

⭐ 二、二叉搜索树的相关操作

⭐2.1二叉搜索树的节点的类型

⭐2.2二叉搜索树的查找（非递归）

⭐ 2.3二叉搜索树的查找（递归）

⭐2.4二叉搜索树的插入（非递归）

⭐2.5二叉搜索树的插入（递归）

⭐2.6二叉搜索树的删除（非递归）

⭐2.7二叉搜索树的删除（递归）

⭐2.8二叉搜索树的遍历

⭐2.9二叉树的拷贝构造及构造，赋值重载

⭐三、二叉搜索树的全部代码

一、二叉搜索树

⭐1.1 二叉搜索树的概念

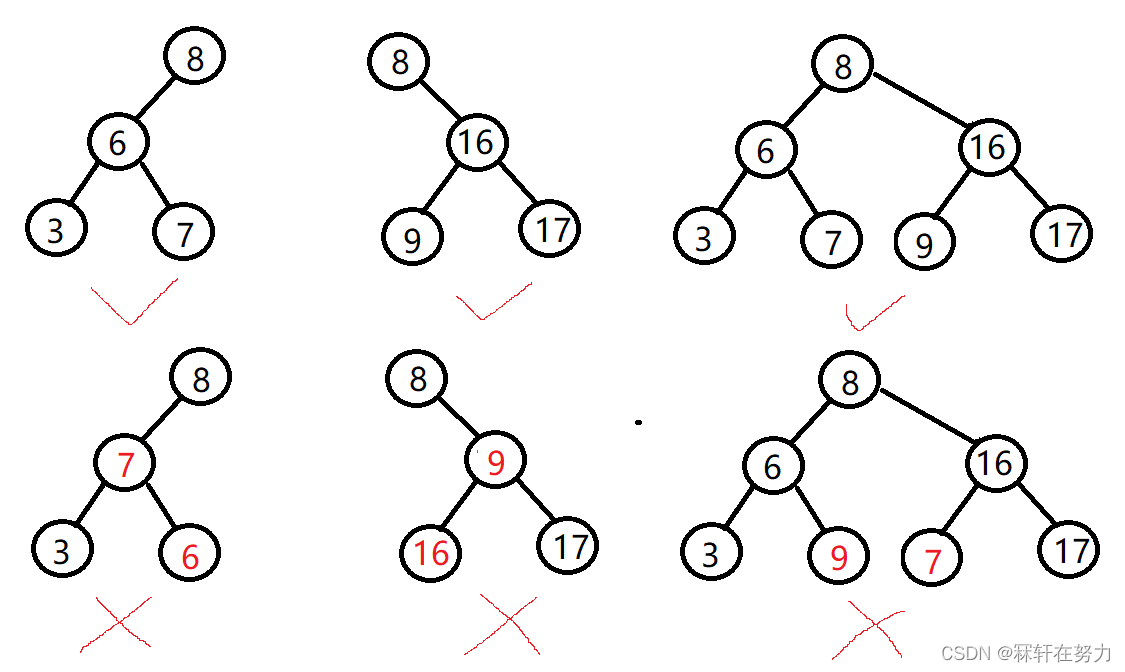
二叉搜索树又称二叉排序树，是一种特殊有序的二叉树。

⭐1.2 二叉搜索树具有的性质：

  • 左子树不为空时，左子树所有节点的值都小于根节点的值
  • 右子树不为空时，右子树所有节点的值都大于根节点的值
  • 当然它的左右子树也满足该性质

d5cc776e54e64213a80051f8edf149a1.png

⭐ 二、二叉搜索树的相关操作

①二叉搜索树的查找

②二叉搜索树的插入

③二叉搜索树的删除

⭐2.1二叉搜索树的节点的类型

template <class K>//类模板
struct BSTNode
{
	BSTNode* left;
	BSTNode* right;
	K _key;
	BSTNode(K key)
		:left(nullptr)
		, right(nullptr)
		, _key(key)
	{}
};

⭐2.2二叉搜索树的查找（非递归）

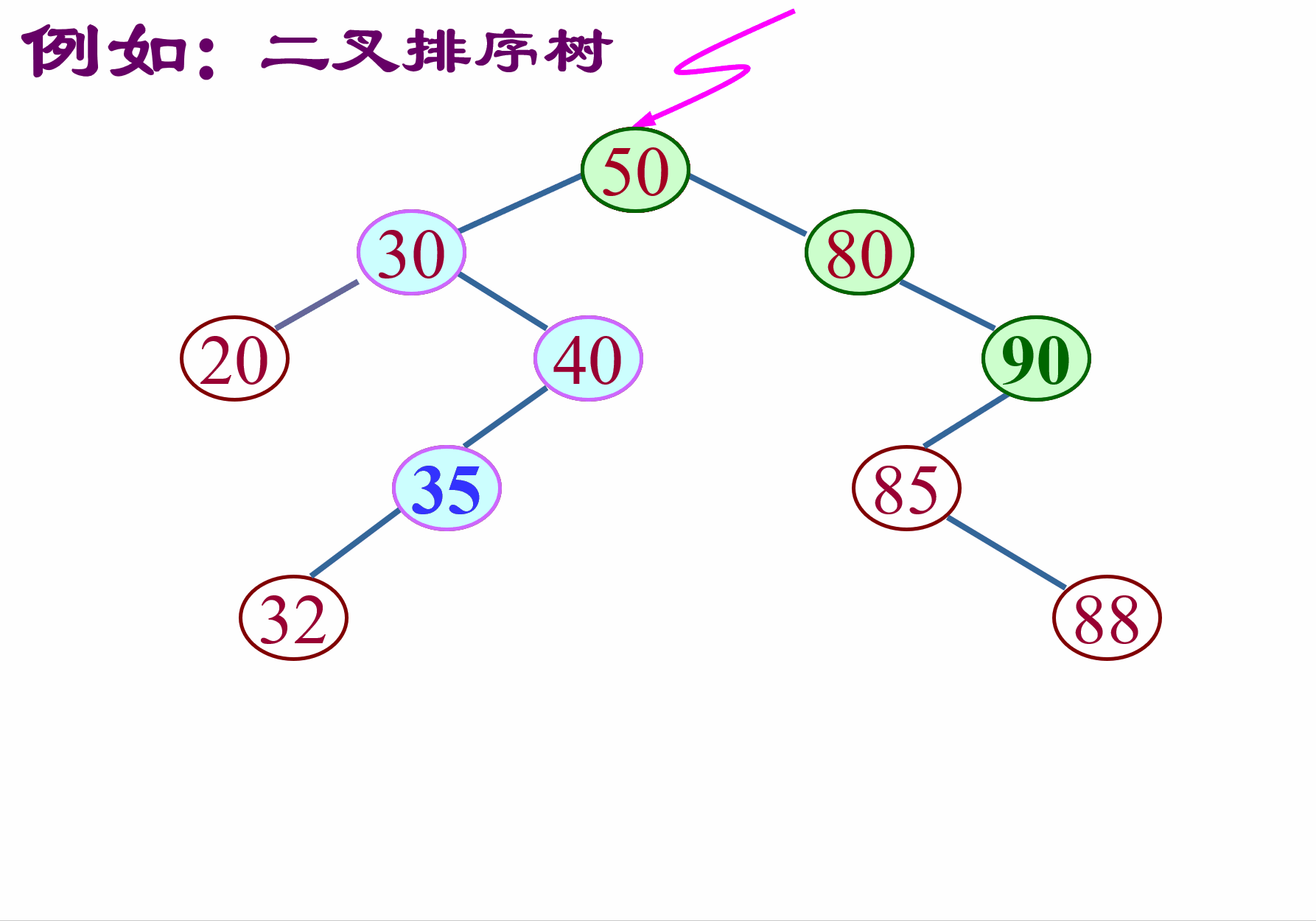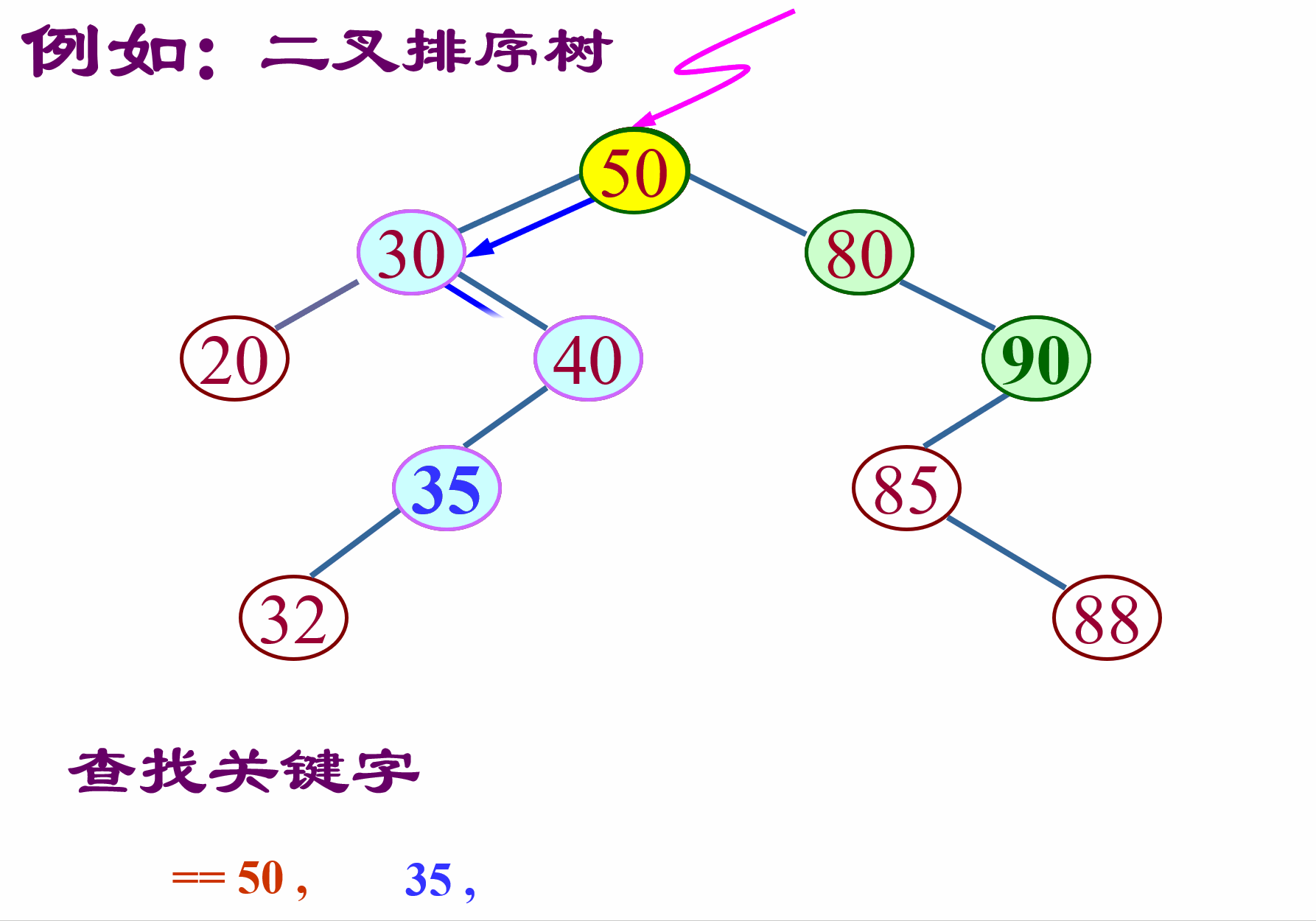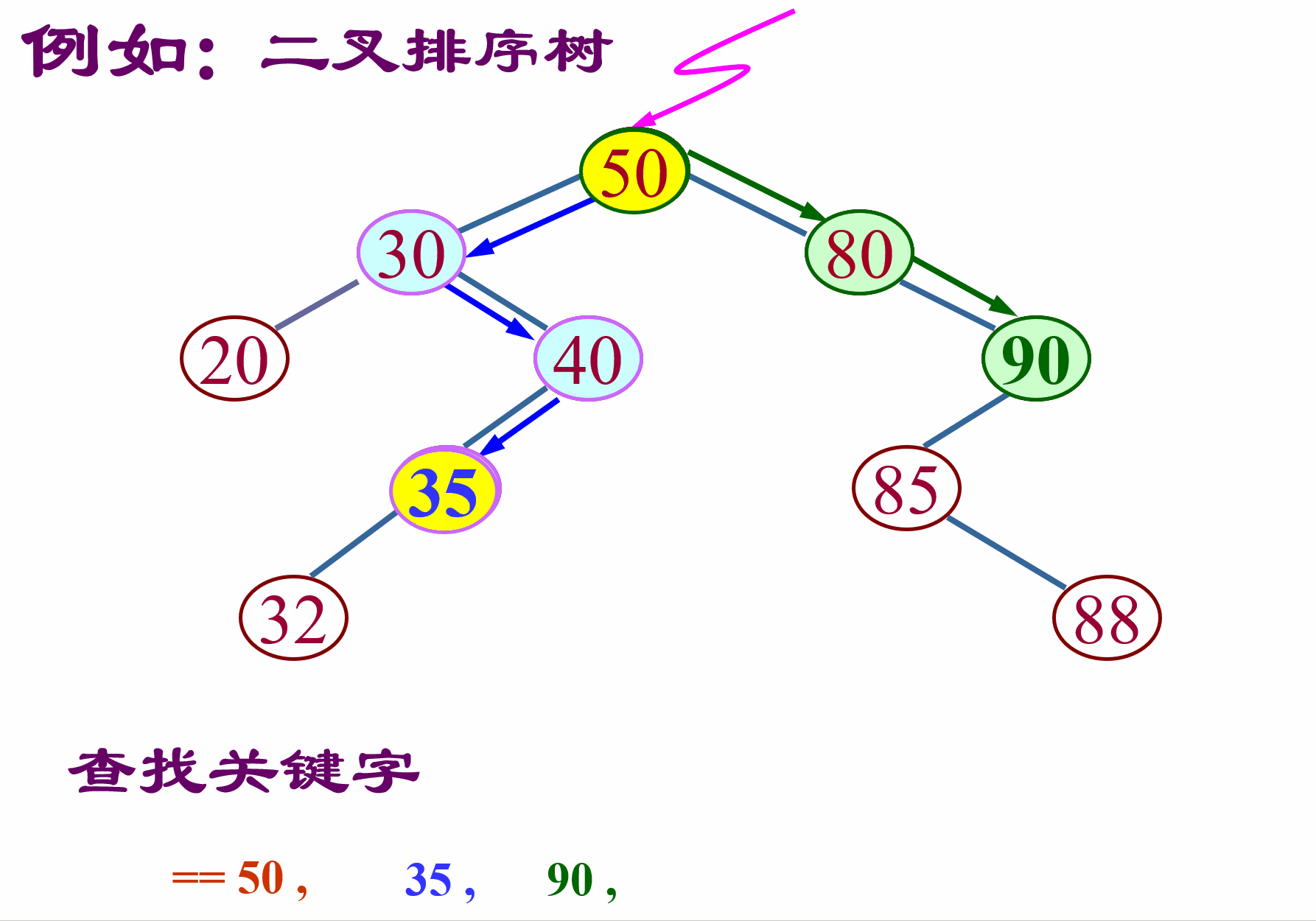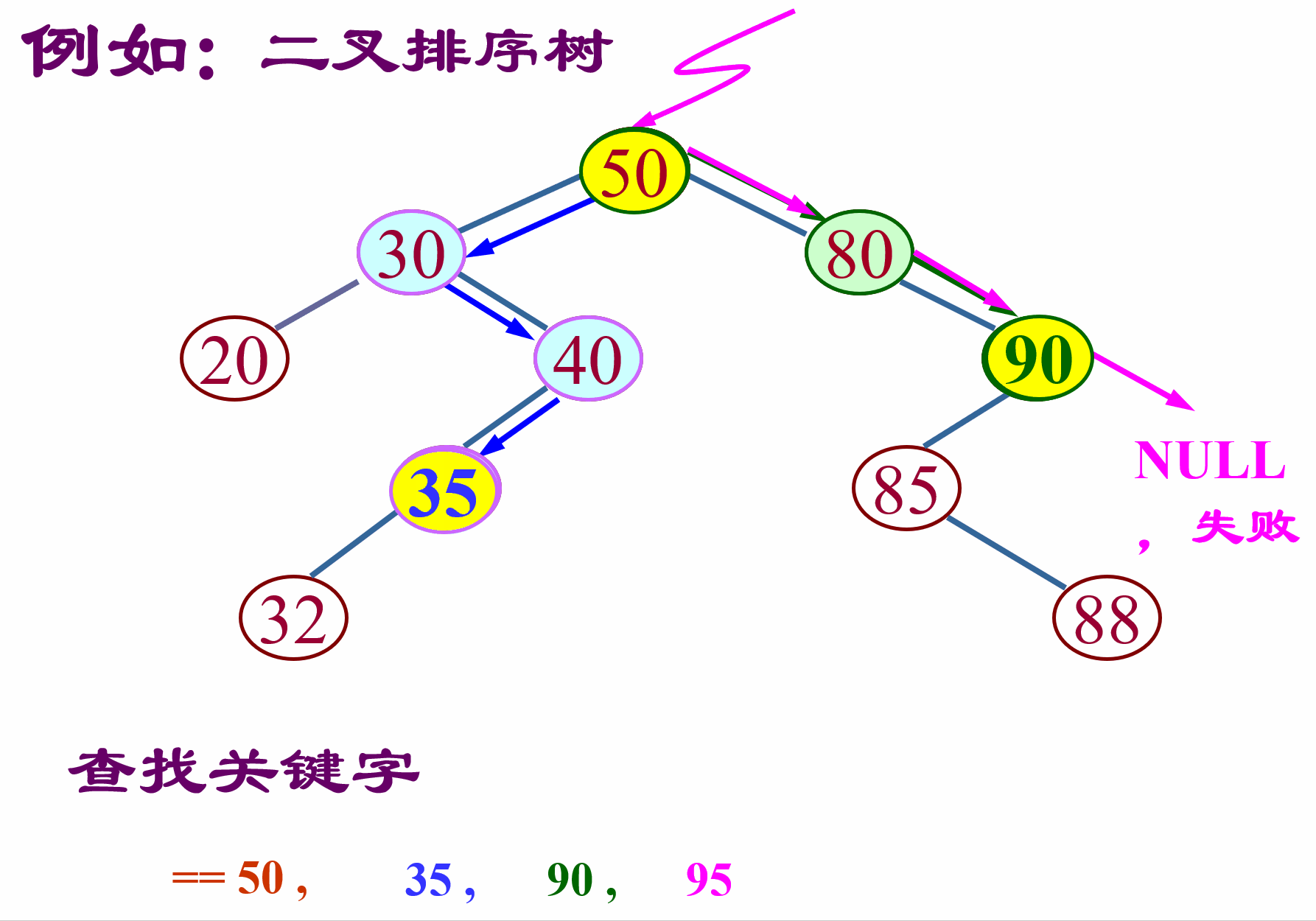
从根开始查找，如果要查找的值比根节点大就往右子树走，如果比根节点小就往左子树走，依次循环，直到找到或走到空，则结束。找到则返回true，找不到返回false。

 

bool find(const K& key)
	{
		BSTNode<K>* cur = _root;
		while (cur)
		{
			if (cur->_key == key)
				return true;
			else if (cur->_key < key)
				cur = cur->right;
			else
				cur = cur->left;
		}
		return false;
	}

⭐ 2.3二叉搜索树的查找（递归）

思路和非递归是一样的，如果查找的节点为空表示该树中没有该节点，返回false，如果找到了就返回true

bool _findR(BSTNode<K>* root, const K& key)
	{
		if (!root)return false;
		if (root->_key == key)
			return true;
		else if (root->_key > key)
			return _findR(root->left, key);//往左子树走
		else
			return _findR(root->right, key);//往右子树走
	}

⭐2.4二叉搜索树的插入（非递归）

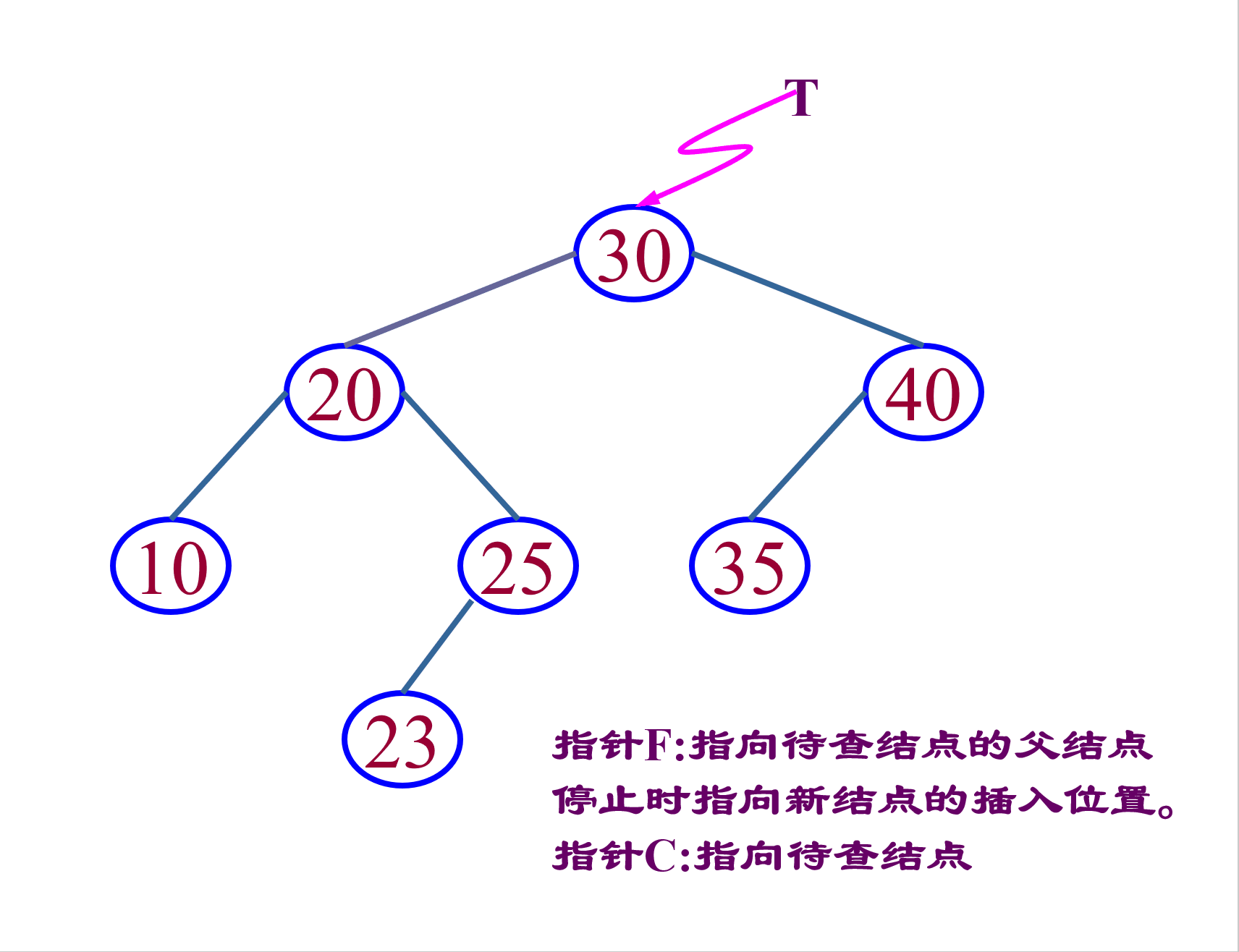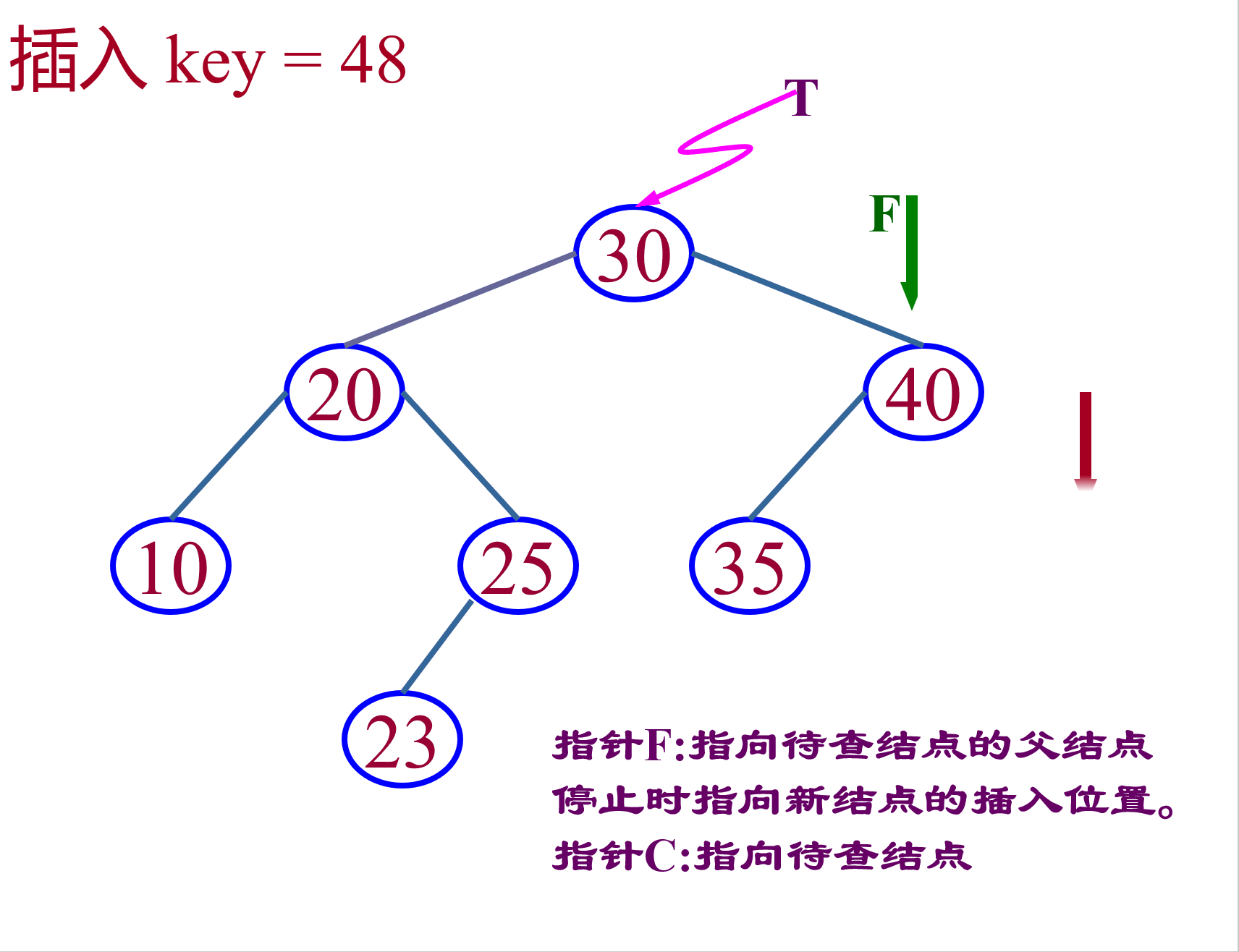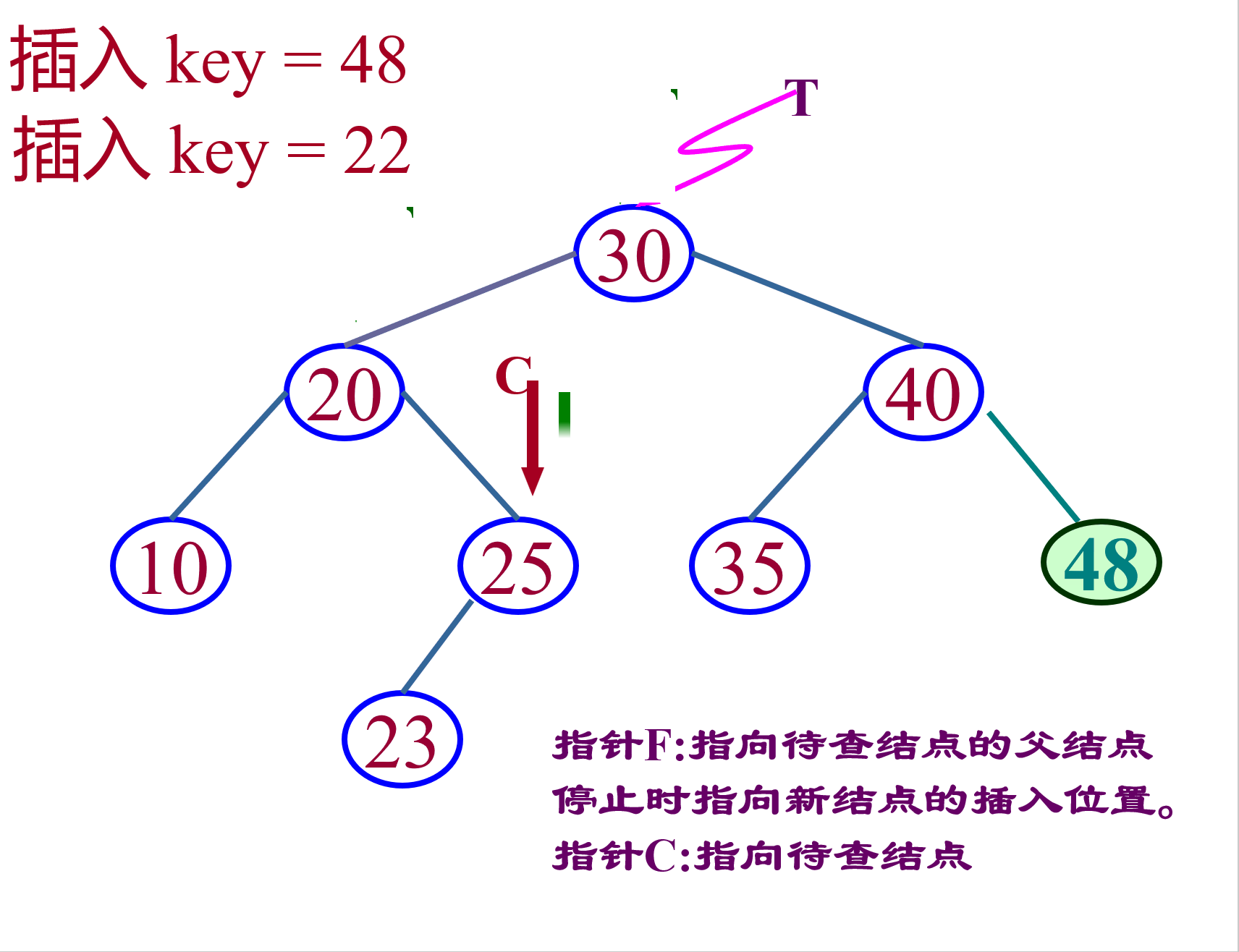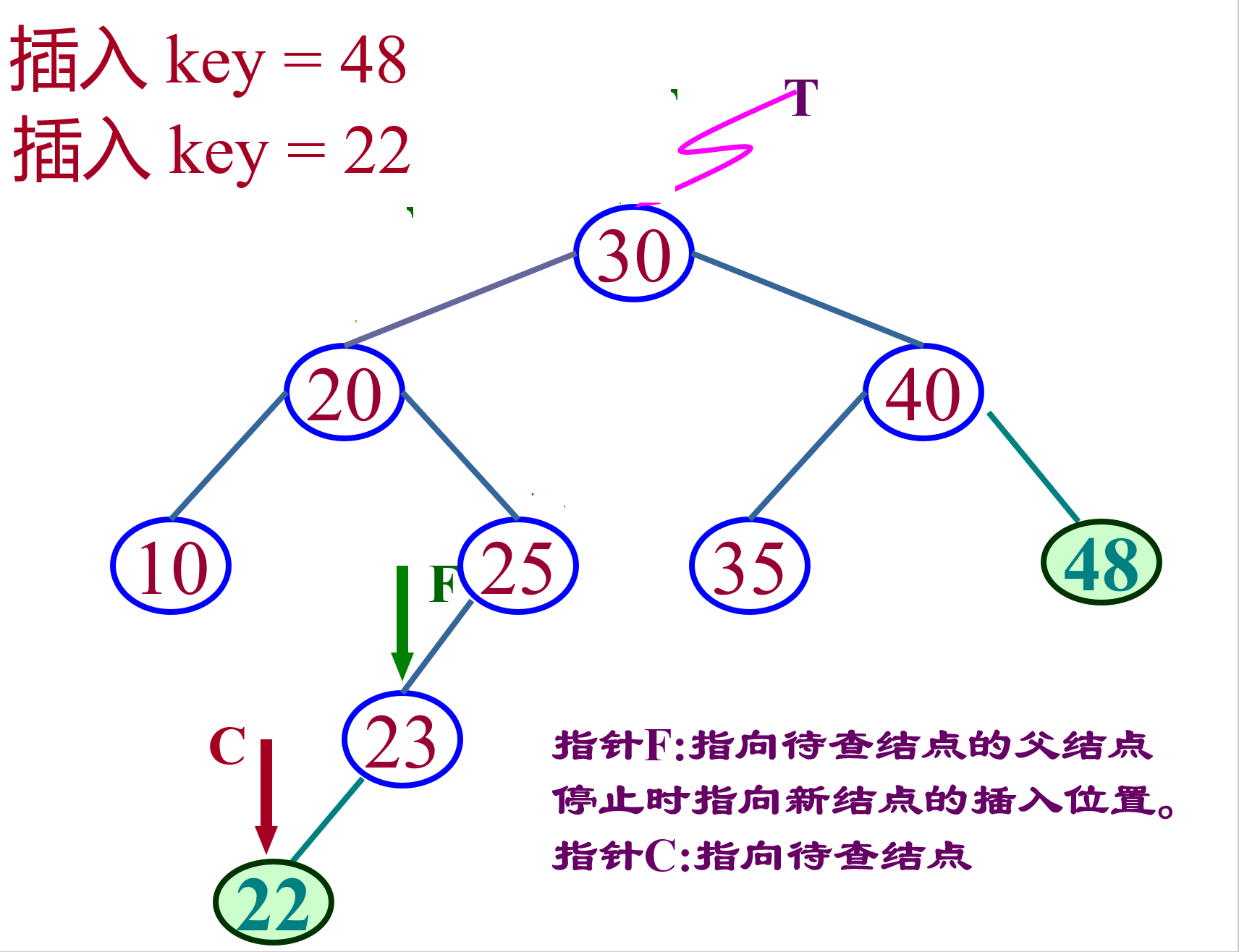
判断树是否为空，如果树为空的话，那么直接新增一个节点，并把该节点的地址赋给_root指针（指向根节点的指针）。如果树不为空，那么就按照二叉搜索树的查找方法，找到插入的位置，然后将新节点插入。注意：如果相等那么将返回false，不能插入

 

bool insert(const K& key)
	{
		if (_root == nullptr)
		{
			_root= new BSTNode<K>(key);
			return true;
		}

		BSTNode<K>* cur = _root, *parent=nullptr;
		while (cur)
		{
			if (_root->_key < key)
			{
				parent = cur;
				cur = cur->right;
			}
			else if (_root->_key > key)
			{
				parent = cur;
				cur = cur->left;
			}
			else
				return false;
		}

		BSTNode<K>* newnode = new BSTNode<K>(key);
		if (parent->_key < key)
		{  //插入的节点大于该插入位置的父节点，往右边插入
			parent->right = newnode;
		}
		else
        { //插入的节点小于该插入位置的父节点，往左边插入
			parent->left = newnode;
        } 
		return true;
	}

⭐2.5二叉搜索树的插入（递归）

这里传的是引用，形参的改变可以影响实参，所以直接给root赋值了

bool _InsertR(BSTNode<K>*& root, const K& key)
	{   //如果根节点为空，直接把值赋给root
		if (!root)
			BSTNode<K>* root = new BSTNode<K>(key);
		if (root->_key > key)
		{
			return _InsertR(root->left, key);
		}
		else if (root->_key < key)
		{
			return _InsertR(root->right, key);
		}
		else
			return false;

	}

⭐2.6二叉搜索树的删除（非递归）

首先查找元素是否在二叉搜索树中，如果不存在，则返回, 否则要删除的结点可能分下面四种情
况：

  1.  要删除的结点无孩子结点
  2.  要删除的结点只有左孩子结点
  3.  要删除的结点只有右孩子结点
  4.  要删除的结点有左、右孩子结点

看起来有待删除节点有4种情况，实际情况1可以与情况2或者3合并起来，因此真正的删除过程
如下：

  • 情况b：删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点--直接删除
  • 情况c：删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点--直接删除
  • 情况d：在它的右子树中寻找中序下的第一个结点(关键码最小)，用它的值填补到被删除节点中，再来处理该结点的删除问题--替换法删除
bool Erase(const K& key)
	{
		BSTNode<K>* cur = _root, * parent =nullptr;
		while (cur)
		{
			if (cur->_key < key)
			{
				parent = cur;
				cur = cur->right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->left;
			}
			else
			{   //没有左孩子节点
				if (cur->left == nullptr)
				{
					if (parent == nullptr)
					{
						_root = _root->right;
					}
					else if (parent->left == cur)
					{
						parent->left = cur->right;
					}
					else
					{
						parent->right = cur->right;
					}
					delete cur;
				}
                  //没有右孩子节点
				else if (cur->right == nullptr)
				{
					if (parent == nullptr)
					{
						_root = _root->right;
					}
					else if (parent->left == cur)
					{
						parent->left = cur->left;
					}
					else
					{
						parent->right = cur->left;
					}
					delete cur;
				}
                 //左右孩子都有的节点
				else
				{
					BSTNode<K>*minparent = cur;
					BSTNode<K>* minright = cur->right;
					while (minright->left)
					{
						minparent = minright;
						minright = minright->left;
					}
					swap(minright->_key, cur->_key);
					if (minparent->left = minright)
					{
						minparent->left = minright->right;
					}
					else
					{
						minparent->right = minright->right;
					}
					delete minright;
				}
			}
			return true;
		}
		return false;

	}

⭐2.7二叉搜索树的删除（递归）

bool _EraseR(BSTNode<K>*& root, const K& key)//传引用
	{
		if (!root)return false;
		if (root->_key == key)
		{
			BSTNode<K>* del = root;
			// 删除
			if (root->left == nullptr)
			{
				root = root->right;
			}
			else if (root->right == nullptr)
			{
				root = root->left;
			}
			else
			{
				BSTNode<K>* minRight = root->right;
				while (minRight->left)
				{
					minRight = minRight->left;
				}

				swap(root->_key, minRight->_key);
                //交换完以后继续递归删除
				return _EraseR(root->right, key);
			}

			delete del;
			return true;
		}
		else if (root->_key > key)
			return _EraseR(root->left, key);
		else
			return _EraseR(root->right, key);
	}

⭐2.8二叉搜索树的遍历

当创建好二叉搜索树后，我们需要知道自己的相关操作对不对，所以需要遍历二叉搜索树来验证，

那什么遍历方式好呢？这里选的是中序遍历，因为二叉搜索树左边都是小于根节点的，右边都是大于根节点的，所以使用中序遍历可以得到一个呈升序的序列

void _Inorder(BSTNode<K>* root)
	{
		if (!root)return;
		_Inorder(root->left);
		cout << root->_key << ' ';
		_Inorder(root->right);
	}

⭐2.9二叉树的拷贝构造及构造，赋值重载

//C++11支持的编译器强制生成默认构造函数
	//BST() = default;
	BST()//构造
	{}
	
	BSTNode<K>* CopyTree( BSTNode<K>* root)
	{
		if (root == nullptr)
			return nullptr;

		BSTNode<K>* copyNode = new BSTNode<K>(root->_key);
		copyNode->_left = CopyTree(root->_left);
		copyNode->_right = CopyTree(root->_right);

		return copyNode;
	}
	BST(const BST<K>& bst)//拷贝构造
	{
		_root = CopyTree(bst);
	}
	
	BST<K>& operator=(const BST<K> bst)//赋值重载
	{
		swap(_root, bst._root);
		return *this;
	}

⭐三、二叉搜索树的全部代码

#pragma once
#include<iostream>
using namespace std;

template <class K>
struct BSTNode
{
	BSTNode* left;
	BSTNode* right;
	K _key;
	BSTNode(K key)
		:left(nullptr)
		, right(nullptr)
		, _key(key)
	{}
};

template <class K>
class BST
{
public:
	//C++11支持的编译器强制生成默认构造函数
	//BST() = default;
	BST()
	{}
	
	BSTNode<K>* CopyTree( BSTNode<K>* root)
	{
		if (root == nullptr)
			return nullptr;

		BSTNode<K>* copyNode = new BSTNode<K>(root->_key);
		copyNode->_left = CopyTree(root->_left);
		copyNode->_right = CopyTree(root->_right);

		return copyNode;
	}
	BST(const BST<K>& bst)
	{
		_root = CopyTree(bst);
	}
	
	BST<K>& operator=(const BST<K> bst)
	{
		swap(_root, bst._root);
		return *this;
	}

	bool find(const K& key)
	{
		BSTNode<K>* cur = _root;
		while (cur)
		{
			if (cur->_key == key)
				return true;
			else if (cur->_key < key)
				cur = cur->right;
			else
				cur = cur->left;
		}
		return false;
	}


	bool insert(const K& key)
	{
		if (_root == nullptr)
		{
			_root= new BSTNode<K>(key);
			return true;
		}
		BSTNode<K>* cur = _root, *parent=nullptr;
		while (cur)
		{
			if (_root->_key < key)
			{
				parent = cur;
				cur = cur->right;
			}
			else if (_root->_key > key)
			{
				parent = cur;
				cur = cur->left;
			}
			else
				return false;
		}
		BSTNode<K>* newnode = new BSTNode<K>(key);
		if (parent->_key < key)
		{
			parent->right = newnode;
		}
		else
			parent->left = newnode;
		return true;
	}


	bool Erase(const K& key)
	{
		BSTNode<K>* cur = _root, * parent =nullptr;
		while (cur)
		{
			if (cur->_key < key)
			{
				parent = cur;
				cur = cur->right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->left;
			}
			else
			{
				if (cur->left == nullptr)
				{
					if (parent == nullptr)
					{
						_root = _root->right;
					}
					else if (parent->left == cur)
					{
						parent->left = cur->right;
					}
					else
					{
						parent->right = cur->right;
					}
					delete cur;
				}
				else if (cur->right == nullptr)
				{
					if (parent == nullptr)
					{
						_root = _root->right;
					}
					else if (parent->left == cur)
					{
						parent->left = cur->left;
					}
					else
					{
						parent->right = cur->left;
					}
					delete cur;
				}
				else
				{
					BSTNode<K>*minparent = cur;
					BSTNode<K>* minright = cur->right;
					while (minright->left)
					{
						minparent = minright;
						minright = minright->left;
					}
					swap(minright->_key, cur->_key);
					if (minparent->left = minright)
					{
						minparent->left = minright->right;
					}
					else
					{
						minparent->right = minright->right;
					}
					delete minright;
				}
			}
			return true;
		}
		return false;

	}

	void Inorder()
	{
		_Inorder(_root);
		cout << endl;
	}
	bool findR(const K& key)
	{
		return _findR(_root, key);
	
	}

	bool InsertR(const K& key)
	{
		return _InsertR(_root, key);	
	}
	bool EraseR(const K& key)
	{
		return _EraseR(_root, key);
	}

private:
	void _Inorder(BSTNode<K>* root)
	{
		if (!root)return;
		_Inorder(root->left);
		cout << root->_key << ' ';
		_Inorder(root->right);
	}
	bool _findR(BSTNode<K>* root, const K& key)
	{
		if (!root)return false;
		if (root->_key == key)
			return true;
		else if (root->_key > key)
			return _findR(root->left, key);
		else
			return _findR(root->right, key);
	}

	bool _InsertR(BSTNode<K>*& root, const K& key)
	{
		if (!root)
			BSTNode<K>* root = new BSTNode<K>(key);
		if (root->_key > key)
		{
			return _InsertR(root->left, key);
		}
		else if (root->_key < key)
		{
			return _InsertR(root->right, key);
		}
		else
			return false;

	}

	bool _EraseR(BSTNode<K>*& root, const K& key)
	{
		if (!root)return false;
		if (root->_key == key)
		{
			BSTNode<K>* del = root;
			// 删除
			if (root->left == nullptr)
			{
				root = root->right;
			}
			else if (root->right == nullptr)
			{
				root = root->left;
			}
			else
			{
				BSTNode<K>* minRight = root->right;
				while (minRight->left)
				{
					minRight = minRight->left;
				}

				swap(root->_key, minRight->_key);

				return _EraseR(root->right, key);
			}

			delete del;
			return true;
		}
		else if (root->_key > key)
			return _EraseR(root->left, key);
		else
			return _EraseR(root->right, key);
	}

	BSTNode<K>* _root = nullptr;
};

二叉搜索树的知识就分享到这里了，有什么错误还望指出。

风语者！平时喜欢研究各种技术，目前在从事后端开发工作，热爱生活、热爱工作。

站长推荐