您现在的位置是:首页 >其他 >Java高阶数据结构 & 图的最短路径问题网站首页其他
Java高阶数据结构 & 图的最短路径问题
图的最短路径问题!
Java高阶数据结构 & 图的最短路径问题
图的基础知识博客:传送门
最短路径问题: 从在带权图的某一顶点出发,找出一条通往另一顶点的最短路径,最短也就是沿路径各边的权值总 和达到最小。
一共会讲解三种算法
- Dijkstra算法【单源最短路径】
- Bellman-Ford算法【单源最短路径】
- 改进:SPFA算法
- Floyd-Warshall算法【多源最短路径】
单源最短路径问题: 给定一个图G = ( V , E ) G=(V,E)G=(V,E),求源结点s ∈ V s∈Vs∈V到图中每个结点v ∈ V v∈Vv∈V的最短路径。
多源最短路径问题: 就是找到每个顶点到除本身的顶点的最短路径
两顶点不连通,则不存在最短路径–>∞
在后面的讲解中,就不要联想到邻接矩阵了,这样脑子CPU都要烧烂了,代码实现需要邻接矩阵,而不是图就长成矩阵这么抽象的样子。
- 看原图去分析思考就行了,记住边的代码表达即可
- 比如说,一个顶点连出去的边,在原图中很明显,在邻接矩阵中不明显,但是后续我们要得到连出去的边,我们也有方法呀,所以在算法思考的时候,先不要在意这点!
-
- 算法思路:原图
- 代码实现:根据算法翻译即可
带负权的图,可能可以找到最短路径,也可能找不到
- 带负权回路的图,不存在最短路径
判断方法:
- 一条路径上通过两次一样的顶点,第二次反而更短了,则必然存在一个 负权回路
- 即,这个环的权值和为负数
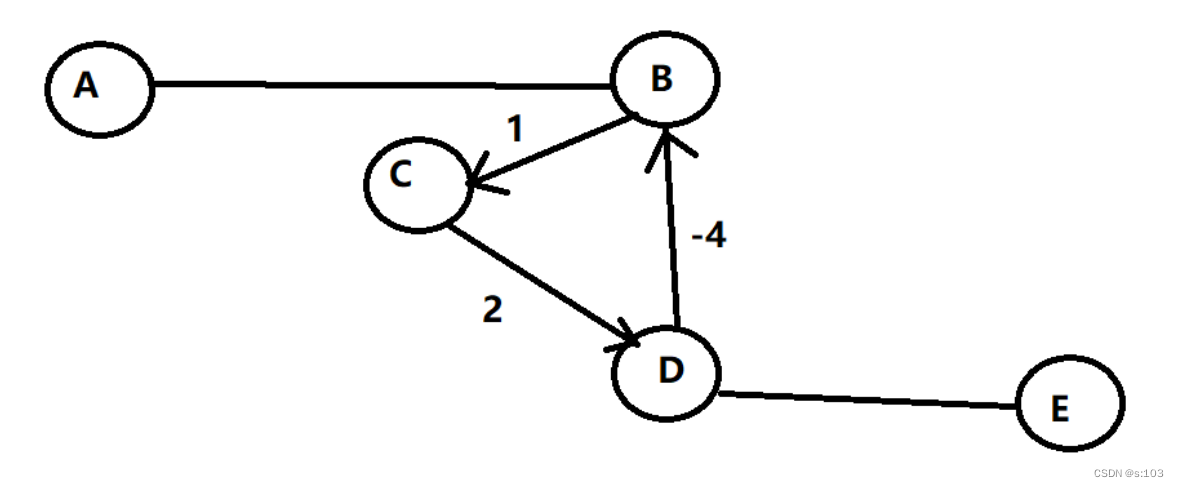
则说明:一张图的最短路径,一定满足边数<= n-1
原因:
因为可以通过这个负权回路,导致一些最短路径趋近于负无穷大
- 即,在这个环里,无限循环
(带负权一定要是有向图,无向图的话,负权边一定构成两个顶点的负权回路)
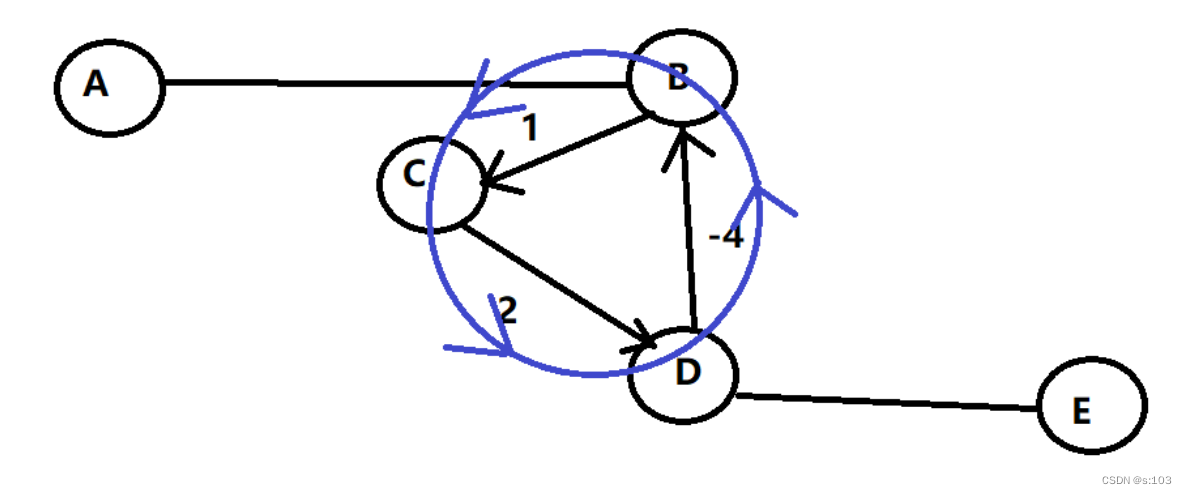
以下算法代码实现简单,重点看算法思想!
1. Dijkstra算法【单源最短路径】
- 思路适用于解决带权重的有向图上的单源最短路径问题
- 无向图当然也可以~
- 但是,算法要求图中的所有边的权重都是非负的~
- 再讲解完算法后你就知道为什么了
定义:(不懂没关系,最后我有详细的证明)
-
定义一个dist数组,这个数组记录出发点到其他点的最短路径
- 一开始没找出来的时候,默认全为无穷大,到自身距离为0
-
定义一个path数组,代表每个顶点的前一个节点
- 通过这个数组可以还原路径
-
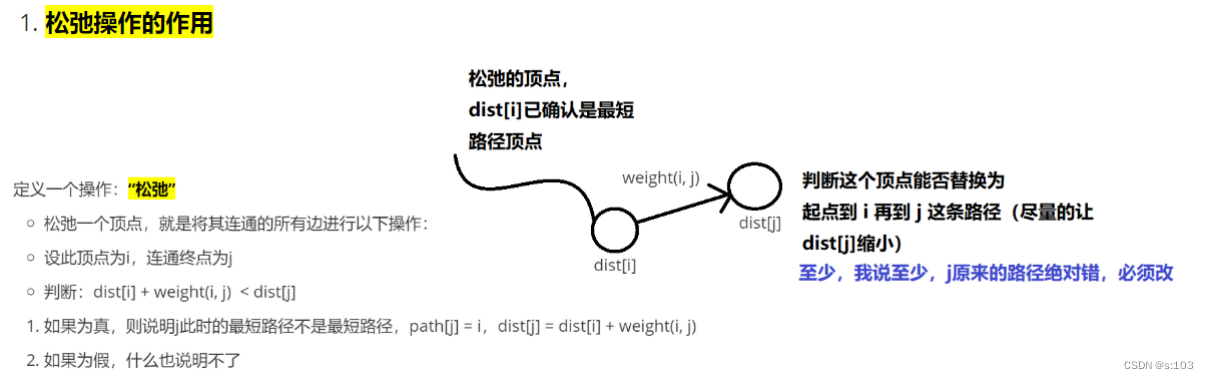
定义一个操作:“松弛”
-
松弛一个顶点,就是将其连通的所有边进行以下操作:
-
设此顶点为i,连通终点为j
-
判断:dist[i] + weight(i, j) < dist[j]
- 如果为真,则说明j此时的最短路径不是最短路径,path[j] = i,dist[j] = dist[i] + weight(i, j)
- 如果为假,什么也说明不了
-
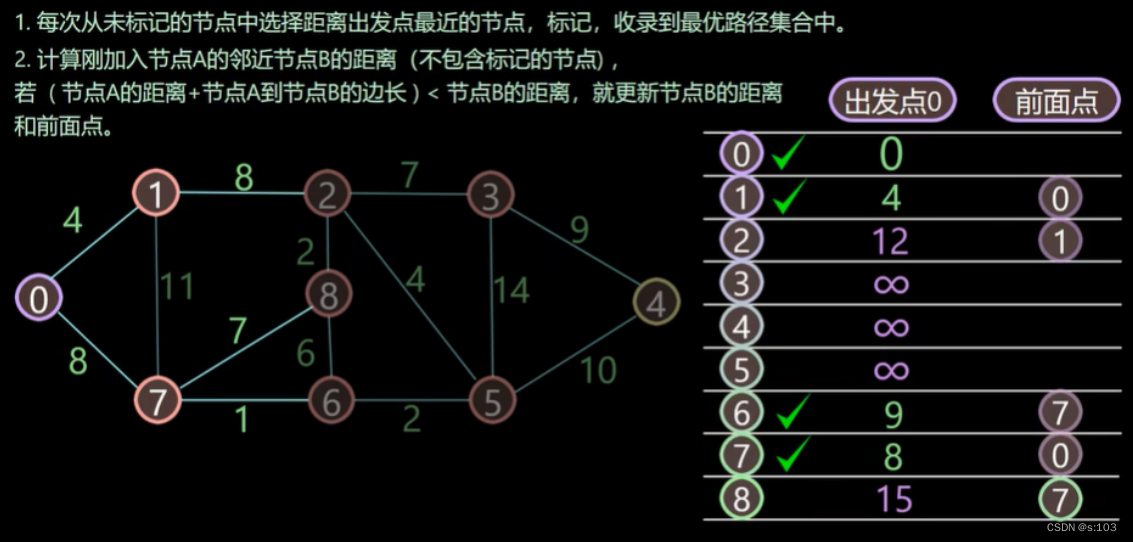
步骤:
- 选取此时dist中的最小元素下标,标记它,断言此顶点为最短路径
- (值为0的出发点此时必然第一个被标记和松弛)
- 松弛刚才被标记的顶点
- 选取松弛完dist中最小元素下标,标记它,断言此顶点为最短路径
- 松弛刚才被标记的顶点
- 选取松弛完dist中最小元素下标,标记它,断言此顶点为最短路径
- 松弛刚才被标记的顶点
- …
- 直到所有顶点都被标记

可以有两种理解方式:
- 标记 松弛 标记 松弛 标记 松弛 … 标记(最后一次没必要松弛)
- 标记最短路径顶点,松弛这个顶点
- (标记出发点后) 松弛 标记 松弛 标记 松弛 标记 … 松弛 标记
- 松弛后诞生一个最短路径,标记
获得最短路径:
- 通过path数组,不断向出发点方向“跳”,直到到达出发点
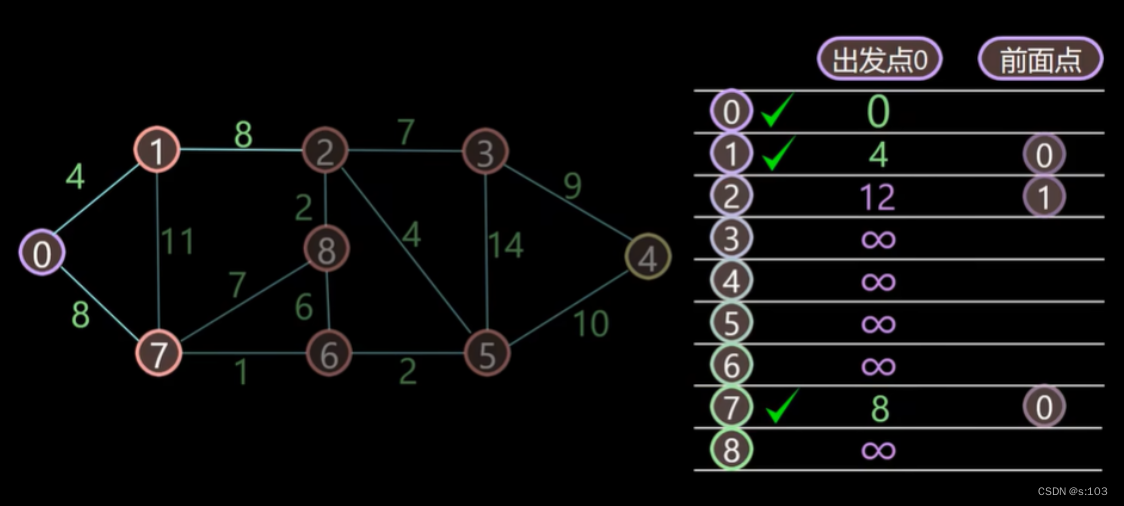
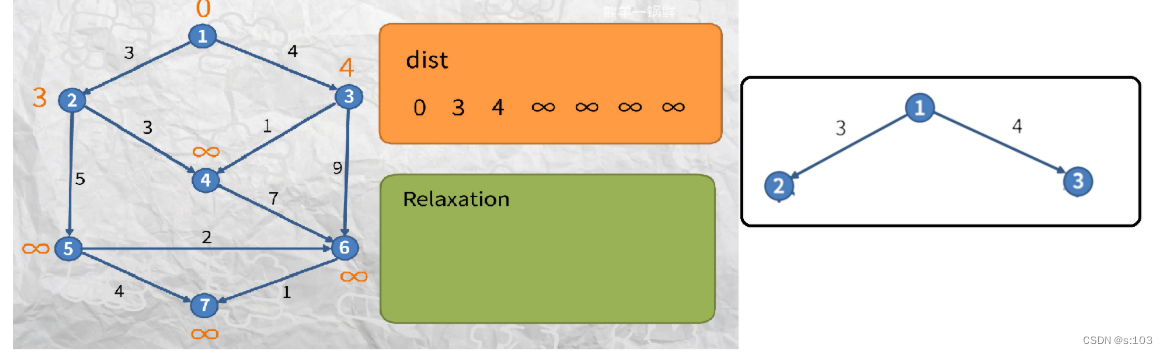
例子:
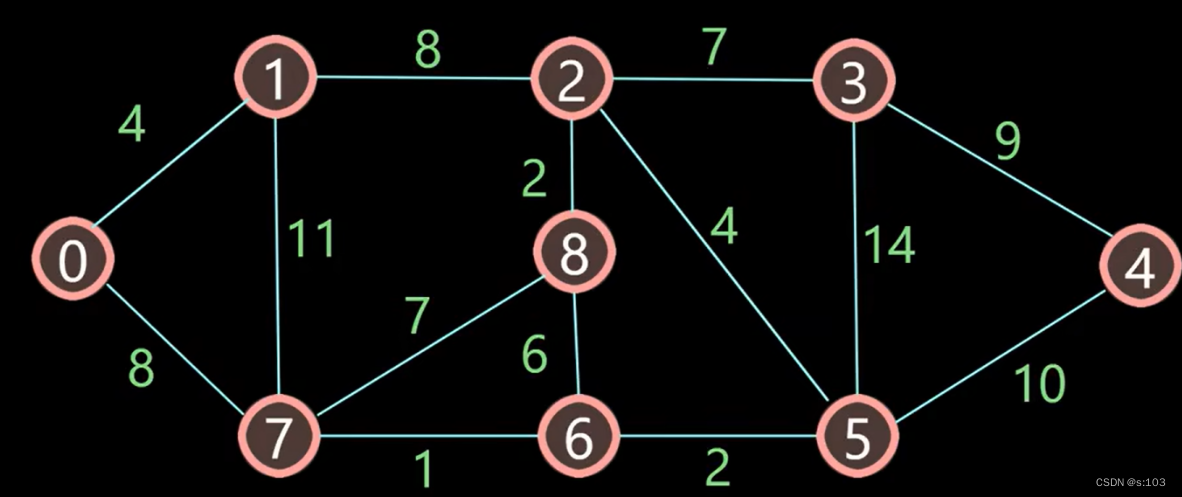
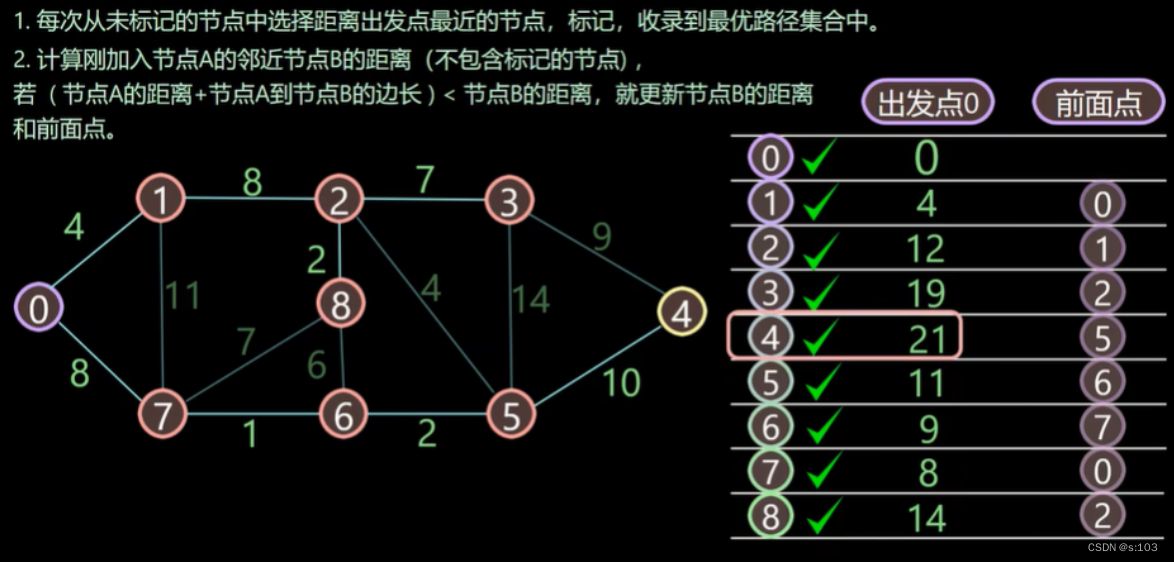
- 如以上连通无向图,求0为出发点,求0到其余点的最短路径
动图演示:
来源:【算法】最短路径查找—Dijkstra算法_哔哩哔哩_bilibili
- 讲的很好!
- 但是没有证明为什么,接下来就来看看为什么吧
1.1 Dijkstra算法证明
- 松弛操作的作用
-
所以,松弛操作,保证了目前看来(再下一次松弛之前),顶点们在dist数组内的中是当前能达到的最小值
-
并且改变j的路径为,【0 , i】延伸一条边【i , j】
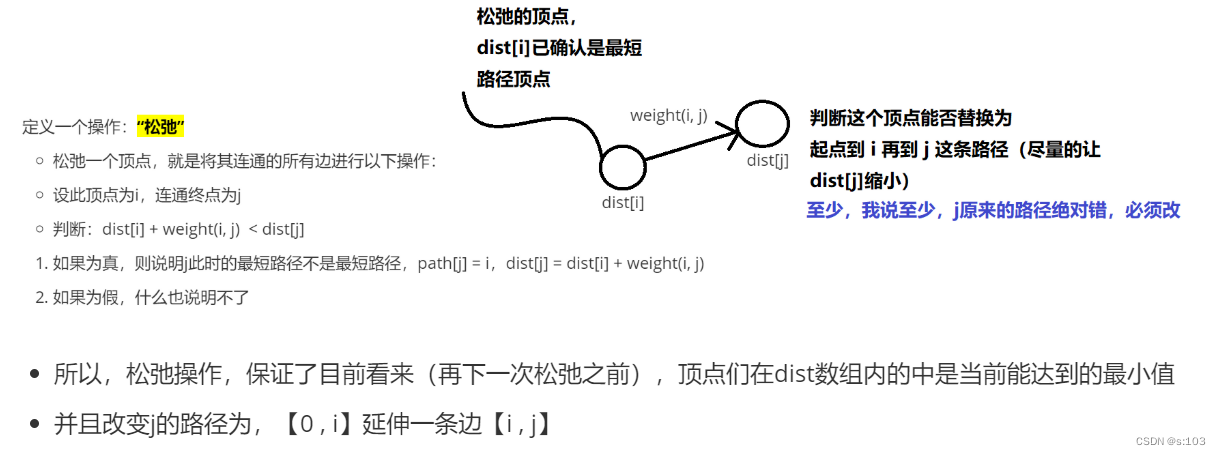
一样短会怎么样呢? -
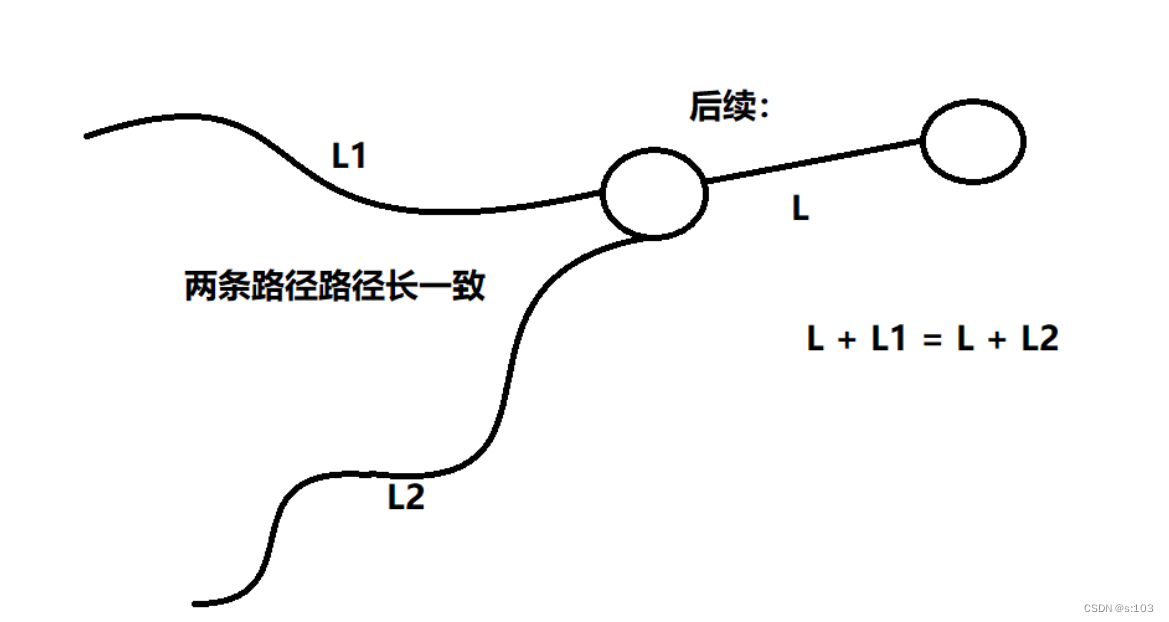
不会怎么样,只是说明最短路径不唯一
至少对这个顶点后续的延伸是没区别的,因为0到j的距离都一样,后续该怎么延伸出去还是怎么延伸出去
- 为什么可以断言这个顶点一定是最短路径?
重要原因:图没有负权
我们按照算法思路先走一走
- 选择0,这是显然的,松弛0后,诞生了“第一代最短路径”(路径上只有1条边)
- 标记松弛后的dist数组(未标记顶点)中最小的顶点
那么我们就断言第一代最短路径中最短的那条路径,就是“正确的”
- 这也是携带了为什么Dijkstra只能解决带非负权图的原因
- 就是因为,它的算法的前提,就是没有负权!
第一代最短路径最短那那条L,就不可能通过任何方式让其更短
- 因为这个点的其他路径就只能是第二代,或者更多
- 而这条路径,是通过第一代最短路径的另一些边的,而这些边本身就比L大,并且此后路径的边都是正的,必然比L大
- 松弛刚才标记的顶点1,诞生“第二代最短路径”(路径上为2条边)
- 标记松弛后的dist数组(未标记顶点)中最小的顶点
那么我们就断言第一代最短路径中最短的那条路径L2,就是“正确的”
同样的道理,这条路径要么是一条边的,要么是两条边的
刚才为什么不一起选择7这个顶点呢?
- 【0到1】 比 【0到7】 短,所以可能【0到1】在到其他顶点,再回到7这个顶点
在第二代最短路径中,松弛操作保证了路径为一条边的和路径为两条边的顶点在dist值最小
- 即,局部范围内,他们是最短路径(在现在能触及的范围内,他们的dist值是正确的)
- 即,以出发点为标准,最多延伸两条边的子图范围内,他们都是最短路径
- 这个子图不包含所有的“两条边的路径”,不包含的部分也不需要出现,因为没有负权,包含在内的“两条边的路径”,是由上一次的最短路径顶点延伸出来的,那么这个条包含在子图内的“两条边的路径”,一定是比不包含的要短~
这一次,最短的是【0到7】,同样的原因,可以断言7此时是正确的最短路径
- 刚才的证明了此时7是这个范围内的最短路径,这就够了
- 后续不会再有到7路径更短的顶点了(别的路径只能增加)
- 松弛顶点7,诞生第三代最短路径
- 标记松弛后dist值(未标记顶点中)最小的顶点
同样的,以出发点为标准,最多延伸三条边的子图(<=3,一样的,不一定包含所有的“三边路径”和“两边路径”,一定包含“更有权威的”路径)范围内,他们都是最短路径
- 选择顶点6(此时顶点6)~
- 因为后续到这顶点就只能增了~
依照这个思路下去,所有顶点被标记,结束!
- 这个例子中,边数最多的路径,为“四边路径”,【0到4】
- 为什么可以通过path确认最短路径?
以【0到4】为例子
【0到4】=【0到5】+【5到4】
- 其实一条长路径一定是由短路径拼接起来的(由刚才的算法得出结论,最短路径的更新,是在前一个顶点的最短路径基础上延伸一条边)
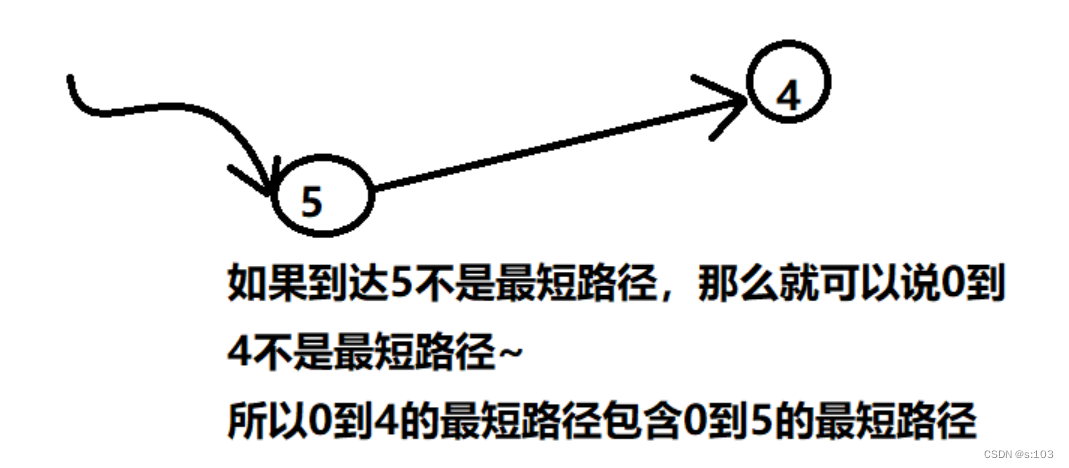
所以,一个最短路径的子路径为别的顶点的最短路径,所以可以通过下标的往回“跳”,得到真实路径
证明完毕~
1.2 Dijkstra算法代码实现
- 代码实现看起来很简单,但是原理是刚才那样的复杂
/**
*
* @param src 出发点
* @param dist 要求把最短路径长存放在这个数组里
* @param path 要求将前面点存放在这个数组里
*/
public void dijkstra(char src, int[] dist, int[] path) {
//获取顶点下标
int srcIndex = getIndexOfV(src);
//初始化dist
Arrays.fill(dist, Integer.MAX_VALUE);
dist[srcIndex] = 0;//起始点
//初始化path
Arrays.fill(path, -1);
path[srcIndex] = srcIndex;//如果是前一个顶点是本身的话,则说明到达起始点
//定义visited数组
int n = arrayV.length;
boolean[] visited = new boolean[n];
//开始标记与松弛操作了
//由于我们知道每次循环都会标记一个,那么循环次数就知道了,所以我们就用特定的for循环去写
for (int i = 0; i < n; i++) {
//找dist最小值
int index = srcIndex;//这个无所谓
int min = Integer.MAX_VALUE;
for (int j = 0; j < n; j++) {
if(!visited[j] && dist[j] < min) {
index = j;
min = dist[j];
}
}
//标记
visited[index] = true;
//松弛
for (int j = 0; j < n; j++) {
//被必要松弛到标记的顶点的,因为没用(再之前的证明中),你要也可以
if(!visited[j] && matrix[index][j] != Integer.MAX_VALUE
&& dist[index] + matrix[index][j] < dist[j]) {
//松弛导致的更新操作,更新其路径为【0,index】延伸一条边【index,j】
dist[j] = dist[index] + matrix[index][j];
path[j] = index;
}
}
}
}
测试:
打印路径和路径长的方法:
public void printShortPath(char vSrc,int[] dist,int[] pPath) {
//1. 获取顶点下标
int srcIndex = getIndexOfV(vSrc);
int n = arrayV.length;
//2、遍历pPath数组 的n个 值,
// 每个值到起点S的 路径都打印一遍
for (int i = 0; i < n; i++) {
//自己到自己的路径不打印
if(i != srcIndex) {
ArrayList<Integer> path = new ArrayList<>();
int parentI = i;
while (parentI != srcIndex) {
path.add(parentI);
parentI = pPath[parentI];
}
path.add(srcIndex);
//翻转path当中的路径
Collections.reverse(path);
for (int pos : path) {
System.out.print(arrayV[pos] +" -> ");
}
System.out.println(dist[i]);
}
}
}
测试案例:
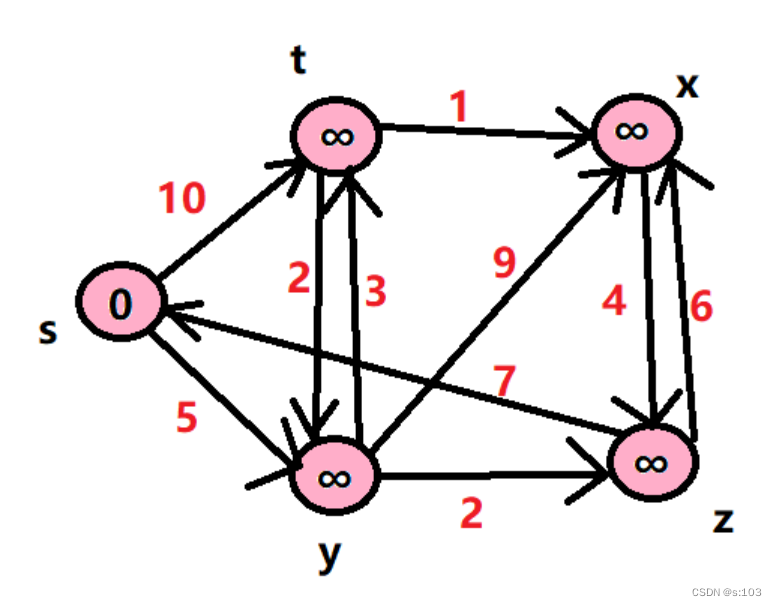
public static void testGraphDijkstra() {
String str = "syztx";
char[] array = str.toCharArray();
GraphByMatrix g = new GraphByMatrix(str.length(),true);
g.initArrayV(array);
g.addEdge('s', 't', 10);
g.addEdge('s', 'y', 5);
g.addEdge('y', 't', 3);
g.addEdge('y', 'x', 9);
g.addEdge('y', 'z', 2);
g.addEdge('z', 's', 7);
g.addEdge('z', 'x', 6);
g.addEdge('t', 'y', 2);
g.addEdge('t', 'x', 1);
g.addEdge('x', 'z', 4);
/*
搞不定负权值
String str = "sytx";
char[] array = str.toCharArray();
GraphByMatrix g = new GraphByMatrix(str.length(),true);
g.initArrayV(array);
g.addEdge('s', 't', 10);
g.addEdge('s', 'y', 5);
g.addEdge('t', 'y', -7);
g.addEdge('y', 'x', 3);
*/
int[] dist = new int[array.length];
int[] parentPath = new int[array.length];
g.dijkstra('s', dist, parentPath);
g.printShortPath('s', dist, parentPath);
}
public static void main(String[] args) {
testGraphDijkstra();
}
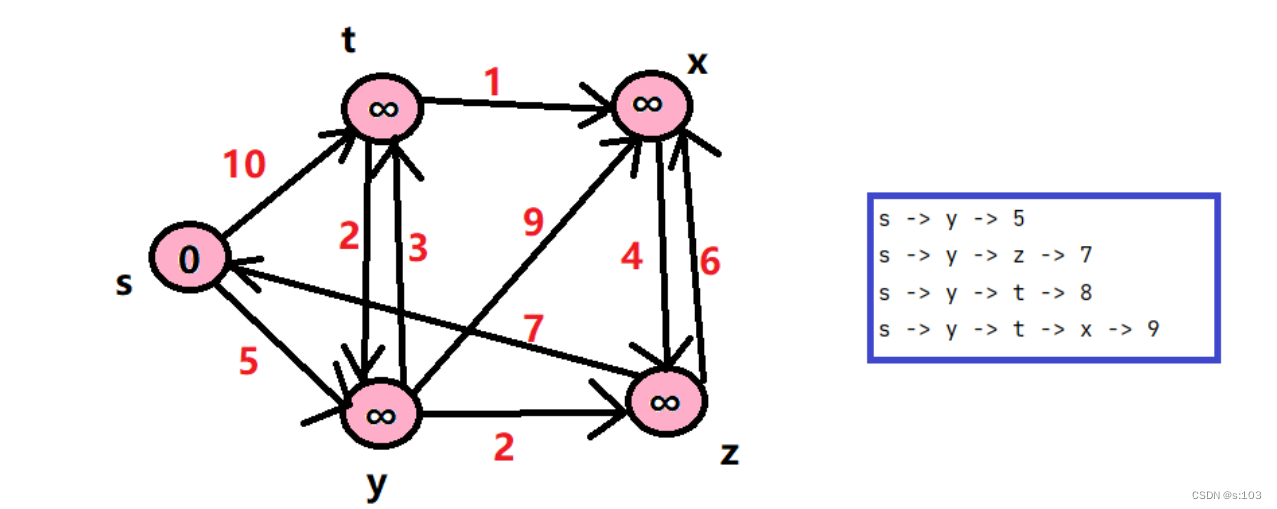
1.3 堆优化的Dijkstra算法
- 时间复杂度为O(N2)
- 标记N次,每次都要遍历数组
- 但是这个原始的算法,适合解决稠密图的最短路径~

- 但如果是稀疏图的话,每次都遍历一次数组,这个复杂度太大了
- 所以有了以下堆优化的算法
本质原理一样:
定义存放在堆里面的类:
class Point {
int index;
int minPath;
}
-
每次松弛都向堆里面放这个对象(而不是改变堆里面对应index的值)
- 堆是如何实现与dist数组一样“更新”的呢?
- 因为我新加入的这个对象,会比堆原本的那个index值的那个值要小,肯定会在其之前被取出
-
取堆顶元素
-
如果这个元素被标记过,达咩,不要(continue)
-
如果这个元素没有被标记过,哟西,标记它,并且对其进行松弛操作
- 标记后,其后面出现遗留的点也无所谓咯
-
而优化后是适合稀疏图的,因为松弛入堆操作的次数可以认为是C常数,那么复杂度为O(N*log2N)
- 但是如果是稠密图,这个松弛入堆操作的次数则会接近于N,算法复杂度到达O(N2*log2N)
- 比不优化的还差
1.4 堆优化Dijkstra算法代码实现
定义Point类:
static class Point {
int indexV;
int distValue;
public Point(int indexV, int distValue) {
this.indexV = indexV;
this.distValue = distValue;
}
}
核心方法:
- 根据的就是刚才的算法!
/**
*
* @param src 出发点
* @param dist 要求把最短路径长存放在这个数组里
* @param path 要求将前面点存放在这个数组里
*/
public void pQDijkstra(char src,int[] dist,int[] path) {
//获得顶点下标
int srcIndex = getIndexOfV(src);
//初始化dist
Arrays.fill(dist, Integer.MAX_VALUE);
dist[srcIndex] = 0;//起始点
//初始化path
Arrays.fill(path, -1);
path[srcIndex] = srcIndex;//如果是前一个顶点是本身的话,则说明到达起始点
//定义visited数组
int n = arrayV.length;
boolean[] visited = new boolean[n];
//定义小根堆
PriorityQueue<Point> queue = new PriorityQueue<Point>(
(o1, o2) -> {
return o1.distValue - o2.distValue;
}
);
queue.offer(new Point(srcIndex, 0));
while(!queue.isEmpty()) {
Point point = queue.poll();
int index = point.indexV;
//被标记过,达咩!
if(visited[index]) {
continue;
}
//标记
visited[index] = true;
//松弛
for (int j = 0; j < n; j++) {
//被必要松弛到标记的顶点的,因为没用(再之前的证明中),你要也可以
if(!visited[j] && matrix[index][j] != Integer.MAX_VALUE
&& dist[index] + matrix[index][j] < dist[j]) {
//松弛导致的更新操作,更新其路径为【0,index】延伸一条边【index,j】
dist[j] = dist[index] + matrix[index][j];
path[j] = index;
queue.offer(new Point(j, dist[j]));
}
}
}
}
测试:
g.pQDijkstra('s', dist, parentPath);
g.printShortPath('s', dist, parentPath);
public static void main(String[] args) {
testGraphDijkstra();
}
- 跟刚才一样的案例
结果一致:
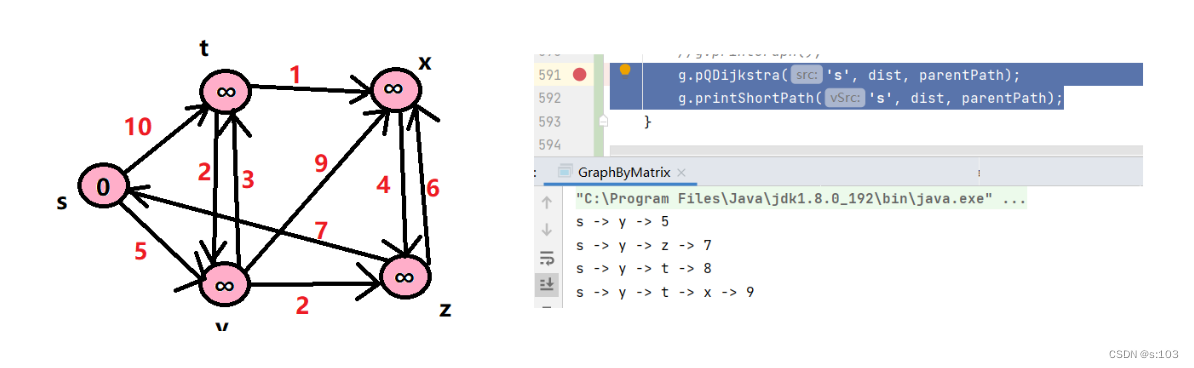
2. Bellman-Ford算法【单源最短路径】
如果把Dijkstra算法称为深度优先,那么Bellman-Ford算法就是广度优先,也更加直接与粗暴
- 简称BF(更暴力算法BF还真对上了O(∩_∩)O哈哈~)
与Dijkstra算法不同,其可以解决带负权的图的最短路径问题!
用到Dijkstra用过的操作:
不同的是它的算法步骤:
- 对全局所有的顶点,都进行一次松弛操作
- 这里不做任何标记,因为现在直接相连的点,最终如果有负权,还是有可能通过“边数更长的最短路径”到达该点
- 这样的操作进行N - 1轮,N为顶点的个数
- 如果这一次没有做任何更新,则以后的松弛也不会有任何的更新,退出循环,结束!
获得最短路径:
- 通过path数组,不断向出发点方向“跳”,直到到达出发点
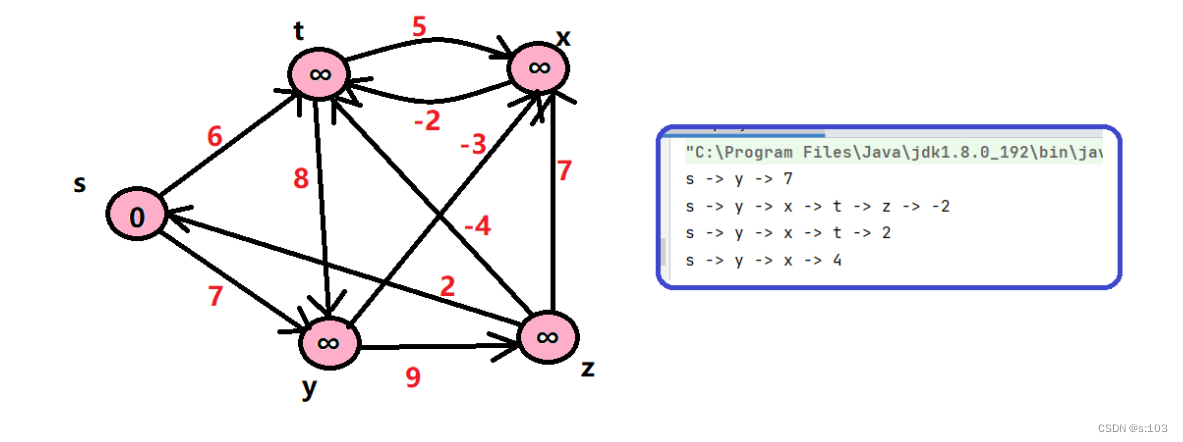
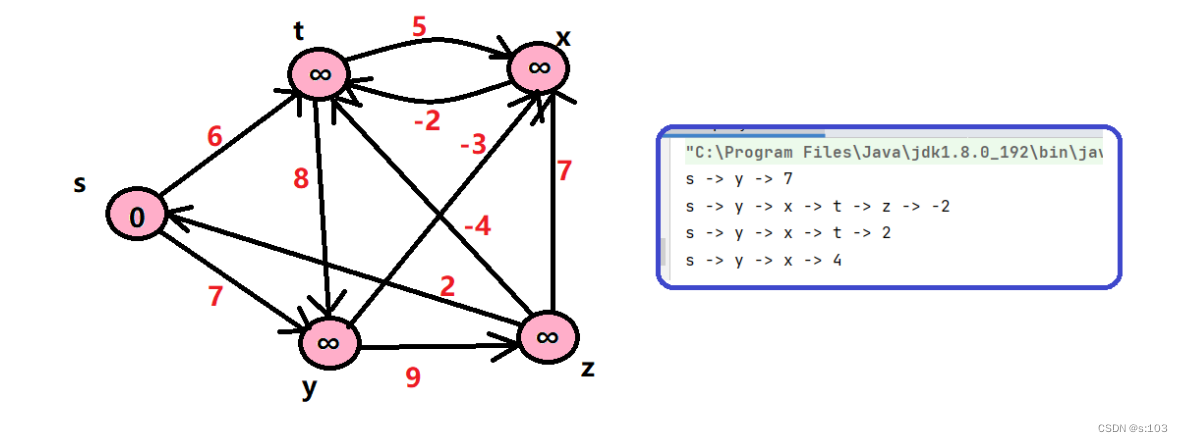
例子:
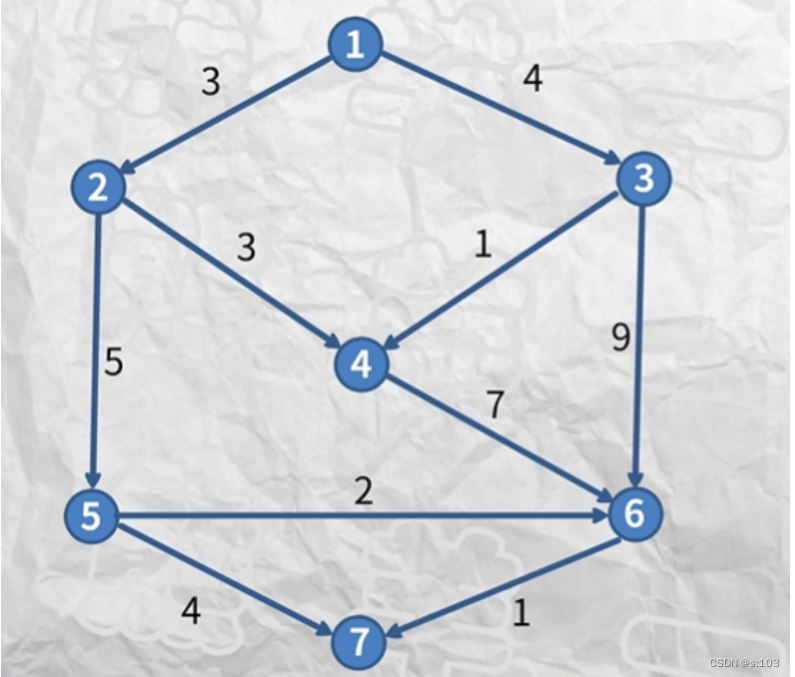
动图演示:](https://img-blog.csdnimg.cn/dfc5201554444726a2979bcafa08c4cb.gif)
来源:【熊羊一锅鲜】Ep.13 单源最短路径Bellman-Ford算法及SPFA算法_哔哩哔哩_bilibili
2.1 BF算法证明
一些点在Dijkstra的证明那已经讲过了
- 不同的一点在于,BF算法松弛操作的顶点,每一次都是所有顶点~
你也会发现,一开始如果先松弛的不是出发点,或者是“已经有路径的顶点”,这个松弛操作是没有意义的,因为这个顶点的dist值为∞
- 这也衍生出了一个问题:顶点松弛的先后会不会有影响
- 第N代最短路径中“边最长为N”的子图范围内,各个顶点的dist值在这个局部范围内【限制路径最多有N条边】是正确的,是最短的
这一点,是 通过松弛操作来保证 的,原本Dijkstra算法没有保证这个子图的完整性,而BF算法由于每次都是松弛所有顶点,所以这个子图是完整的~
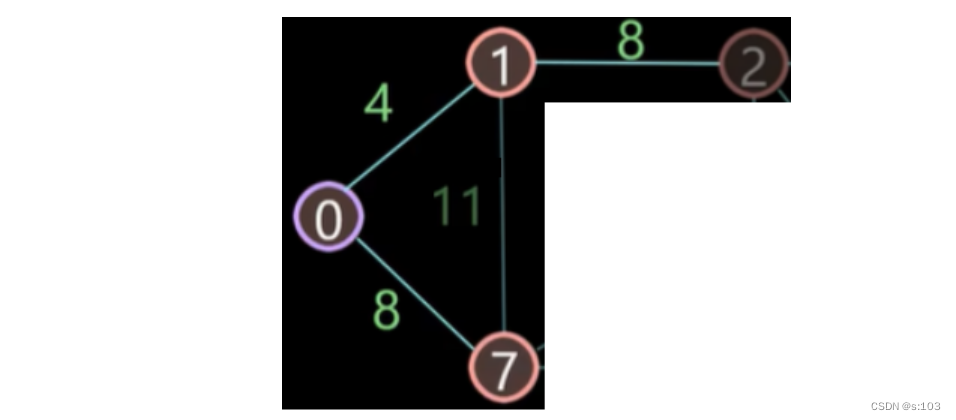
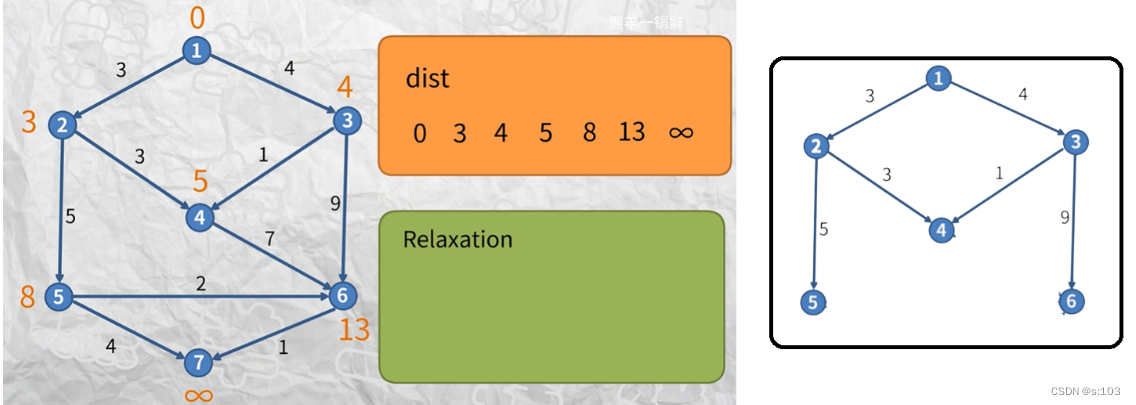
如第一代子图(第一次循环的结果):
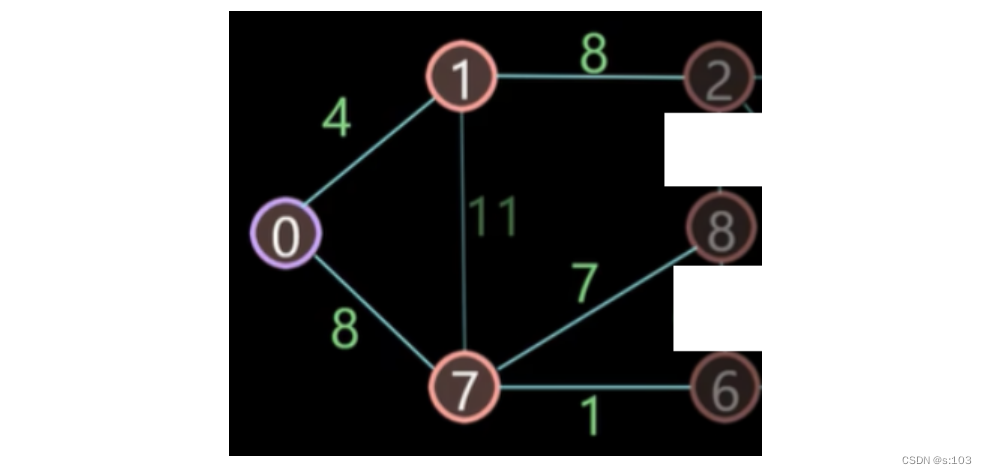
如第二代子图(第二次循环的结果):
如第三代子图(第三次循环的结果):
你可能有一个错觉:这不是已经涉及所有顶点了吗,那么这就是在全局范围内的正确?
否,因为这里限制路径长最大是“三条边”,在这个限制下是正确的
- 例如【0到6】最短为三步,再走一步到7确实是11<12但是,这就是四步了呀
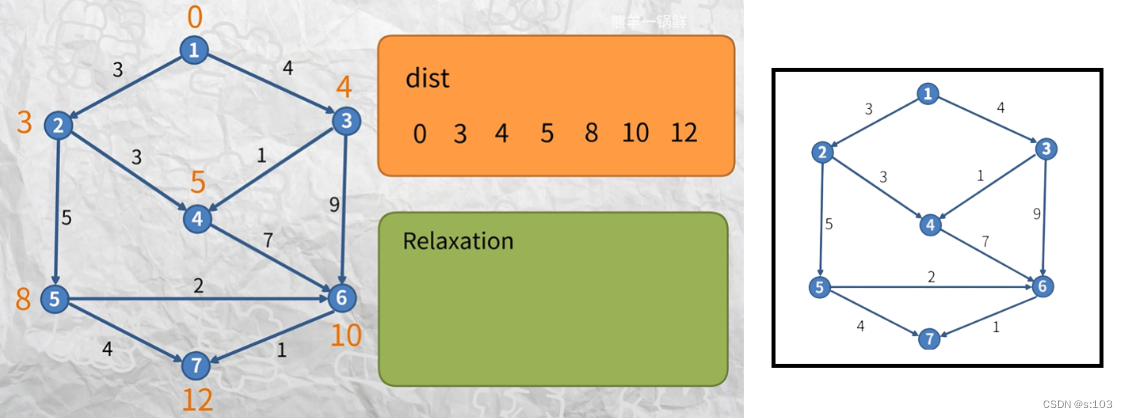
如第四代子图(第四次循环的结果):
到了第五代子图的时候(第五次循环的结果):
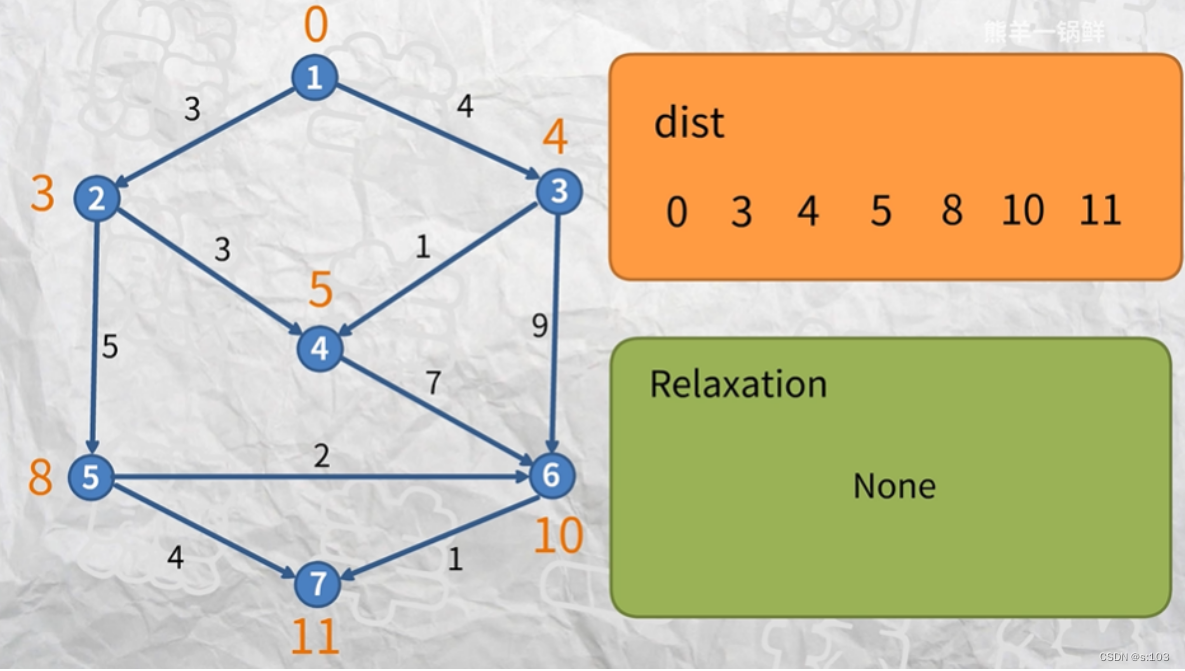
- 所有顶点都没被更新~
- 跳出循环,算法结束
- 说明了里面“最长的最短路径”是四条边的
- 顶点松弛的先后会不会有影响
其实 被松弛涉及到的顶点i有更新的条件 是:顶点j(顶点j松弛后涉及到了顶点i)更新过
而你也发现了这个算法产生了大量的没用操作
- 如果先对“后面”的顶点松弛,可能没有作用
- 假设此次是第n次循环,那么一个顶点目前最短路径边数小于等于n-2的顶点
- 例如第二次循环的时候,出发点没必要松弛
- 第三次循环的时候,最短路径边数为1的顶点没有必要松弛
- 因为松弛完后最多为两条边,而两条边的时候在第二代子图(第二次循环结果)中,已经是得到最短的了
- 所以没有必要!
你可能会觉得,先松弛出发点,那么可能“后面的顶点”也会链式的被更新到
- 但这样,“前面的路径”发生改变,这个“后面的顶点”也有改变的风险
而我们只需要保证这一个严格成立即可
第N代最短路径中“边最长为N”的子图范围内,各个顶点的dist值在这个局部范围内【限制路径最多有N条边】是正确的,是最短的
最坏的情况下,就是完全“逆行”,即使这样,每一代都能够满足这一点
- 因为每个顶点都要松弛
- 顺序不同只是改变其“连锁反应”【就是因为刚才它刚变了,导致我虽然和它都是第n此松弛,但是我却因此可以更新别的顶点】
- 而不会改变其“必然的变化”
- 这必然的变化,不是由于连锁反应产生的
动图分析:(抽象)
- 希望你能get到
- 最后一次循环的更新后,难道不应该再次松弛去更新其他顶点吗?
答:不用,理由就是到达第N - 1次循环,结果是第N-1代子图,这已经到达了“全局范围”,所有顶点的dist值最短路径都是正确的。
-
所有的路径本身就小于等于N - 1,在最后一次循环更新的顶点,则说明其路径达到最长值:n-1条边
-
松弛的作用结果是延伸刚才的路径,那么刚才的路径已经是边数最大,松弛不会成功,没有必要继续松弛了
-
如果是带负权回路的,继续松弛一直都会更新
- 会产生第∞代子图
- 需要循环后去判断~
证明完毕~
2.2 BF算法代码实现
//这也是判断是否有负权回路的算法
public boolean bellmanFord(char src,int[] dist,int[] path) {
//获得顶点下标
int srcIndex = getIndexOfV(src);
//初始化dist
Arrays.fill(dist, Integer.MAX_VALUE);
dist[srcIndex] = 0;//起始点
//初始化path
Arrays.fill(path, -1);
path[srcIndex] = srcIndex;//如果是前一个顶点是本身的话,则说明到达起始点
int n = arrayV.length;
//循环n-1次,每次松弛一个顶点
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++) {
if(matrix[j][k] != Integer.MAX_VALUE &&
matrix[j][k] + dist[j] < dist[k]) {
dist[k] = matrix[j][k] + dist[j];
path[k] = j;
}
}
}
}
//检测负权回路
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
//至于一样短的情况下,无所谓,这就是最短路径不唯一呗~
//
if (matrix[i][j] != Integer.MAX_VALUE
&& matrix[i][j] + dist[i] < dist[j]) {
return false; //false代表了有负权回路
}
}
}
return true;
}
测试案例:
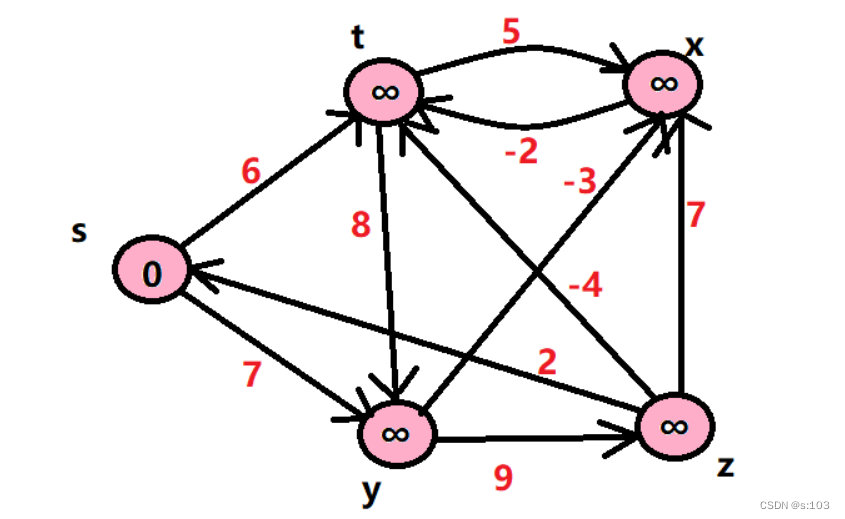
public static void testGraphBellmanFord() {
String str = "syztx";
char[] array = str.toCharArray();
GraphByMatrix g = new GraphByMatrix(str.length(),true);
g.initArrayV(array);
g.addEdge('s', 't', 6);
g.addEdge('s', 'y', 7);
g.addEdge('y', 'z', 9);
g.addEdge('y', 'x', -3);
g.addEdge('z', 's', 2);
g.addEdge('z', 'x', 7);
g.addEdge('t', 'x', 5);
g.addEdge('t', 'y', 8);
g.addEdge('t', 'z', -4);
g.addEdge('x', 't', -2);
//负权回路实例
// g.addEdge('s', 't', 6);
// g.addEdge('s', 'y', 7);
// g.addEdge('y', 'z', 9);
// g.addEdge('y', 'x', -3);
// g.addEdge('y', 's', 1);
// g.addEdge('z', 's', 2);
// g.addEdge('z', 'x', 7);
// g.addEdge('t', 'x', 5);
// g.addEdge('t', 'y', -8);
// g.addEdge('t', 'z', -4);
// g.addEdge('x', 't', -2);
int[] dist = new int[array.length];
int[] parentPath = new int[array.length];
boolean flg = g.bellmanFord('s', dist, parentPath);
if(flg) {
g.printShortPath('s', dist, parentPath);
}else {
System.out.println("存在负权回路");
}
}
public static void main(String[] args) {
testGraphDijkstra();
}
测试一个不带负权回路的案例:
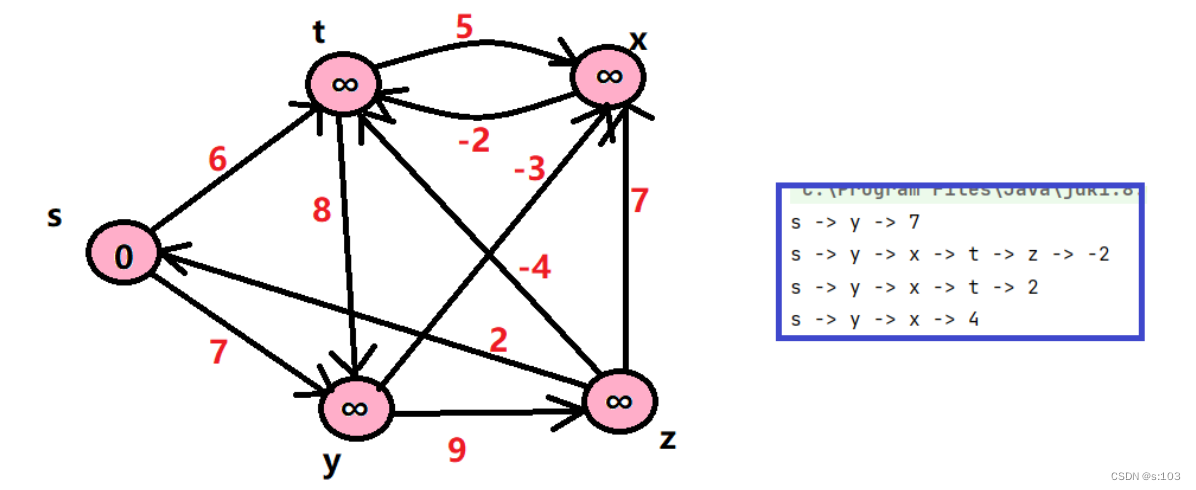
测试带负权回路的:
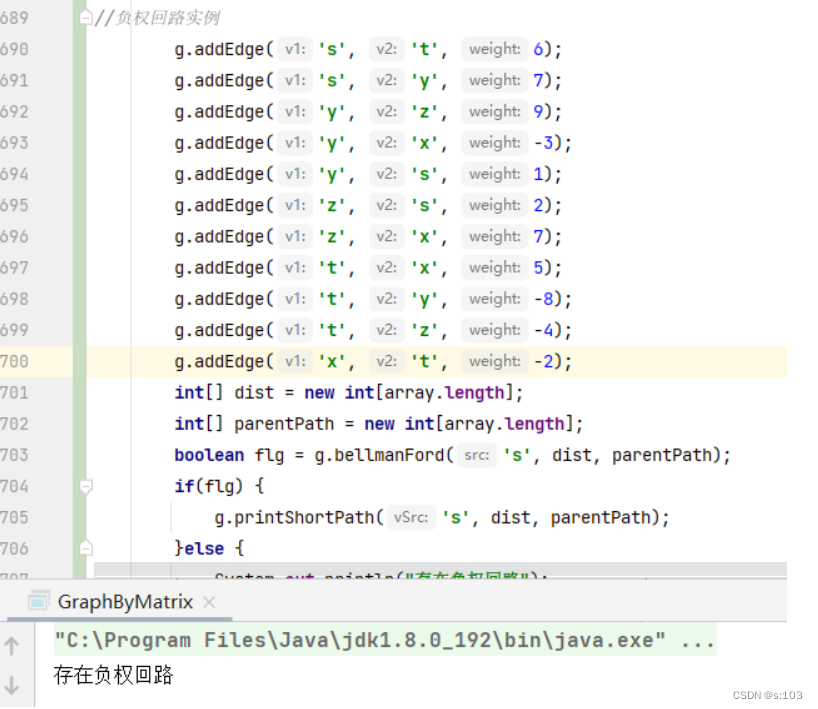
2.3 队列优化的BF算法:SPFA算法
刚才提到:
那么我们只需要松弛更新了的顶点就好了呀,
结合BF的视角:
- 每一次循环更新的顶点,设他们的集合为set1
- 下一次循环更新的顶点,设他们的集合为set2
要想满足BF算法的思想:
- set1的整体要在set2的整体前松弛完才行
- 才能有第一代子图—第二代子图—第三代子图这样的效果
所以用到数据结构:队列
步骤就是:
- 将起始点放入队列
- 循环以下操作
- 取队头得到一个顶点
- 松弛这个顶点
- 直到队列为空,即不再有元素更新,结束算法
显然,这个算法没法判断负权回路的存在,会死循环下去~
2.4 SPFA算法代码实现
public void queueBellmanFord(char src,int[] dist,int[] path) {
//获得顶点下标
int srcIndex = getIndexOfV(src);
//初始化dist
Arrays.fill(dist, Integer.MAX_VALUE);
dist[srcIndex] = 0;//起始点
//初始化path
Arrays.fill(path, -1);
path[srcIndex] = srcIndex;//如果是前一个顶点是本身的话,则说明到达起始点
int n = arrayV.length;
//定义一个队列
Queue<Integer> queue = new LinkedList<>();
queue.offer(srcIndex);
//开始循环松弛
while(!queue.isEmpty()) {
int top = queue.poll();
for (int i = 0; i < n; i++) {
if (matrix[top][i] != Integer.MAX_VALUE
&& matrix[top][i] + dist[top] < dist[i]) {
dist[i] = matrix[top][i] + dist[top];
path[i] = top;
queue.offer(i);
}
}
}
}
测试:
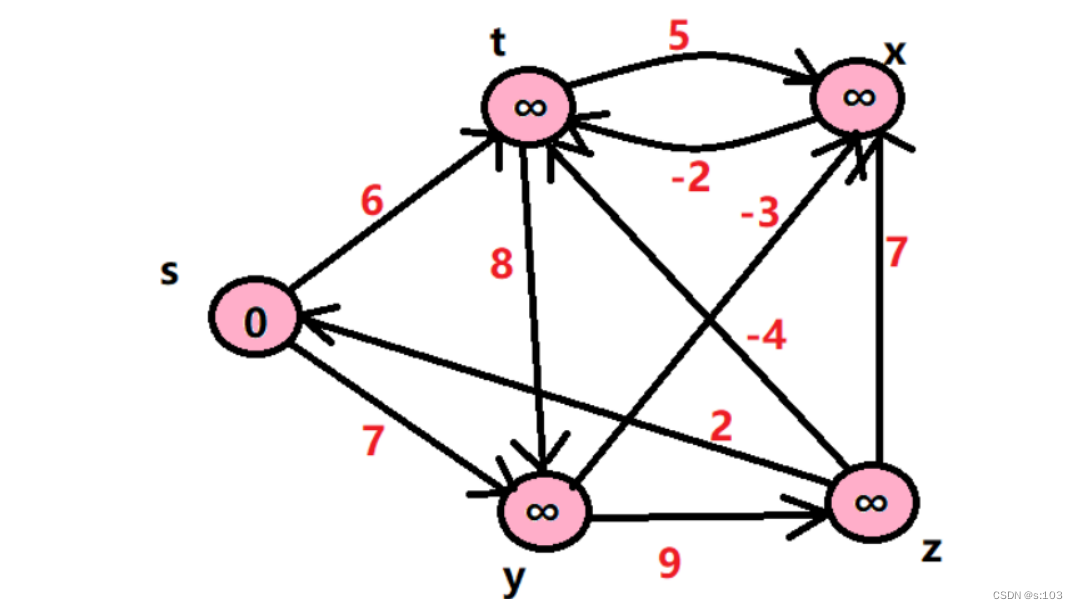
- 带负权回路的案例会死循环,这里就不展示了~
public static void testGraphBellmanFord() {
String str = "syztx";
char[] array = str.toCharArray();
GraphByMatrix g = new GraphByMatrix(str.length(),true);
g.initArrayV(array);
g.addEdge('s', 't', 6);
g.addEdge('s', 'y', 7);
g.addEdge('y', 'z', 9);
g.addEdge('y', 'x', -3);
g.addEdge('z', 's', 2);
g.addEdge('z', 'x', 7);
g.addEdge('t', 'x', 5);
g.addEdge('t', 'y', 8);
g.addEdge('t', 'z', -4);
g.addEdge('x', 't', -2);
int[] dist = new int[array.length];
int[] parentPath = new int[array.length];
g.queueBellmanFord('s', dist, parentPath);
g.printShortPath('s', dist, parentPath);
}
public static void main(String[] args) {
testGraphDijkstra();
}
2.5 复杂度分析
M是边的数量,N是顶点的个数
则BF算法的时间复杂度为O(N * M),而大部分情况下SPFA算法的时间复杂度为O(M),最坏情况是O(N * M)
如果是稠密图的话,M会变得很大很大,两个算法的时间复杂度都会变得很大!
- 所以这两种算法适合去解决带负权的稀疏图~
3. Floyd-Warshall算法【多源最短路径】
3.1 算法思想
但是,值得注意的是:根据相邻顶点之间的权值,要记录下来每个顶点“一条边的路径”!否则这个算法没有用武之地
- 因为dist初始都是无穷大,并且这个算法的步骤没有用到matrix数组,即没有用到权值
并且:最外层循环的循环遍历的应该对应的是中间节点
如果外两层是i,j循环(路线【i到j】),然后最内层循环是k循环(中间节点),这样子是很局限的,因为这i到j再k循环结束后,就被确定了唯一的最短路径,而不是在单单这一次就确定了,这是很不合理的。
- 因为在后面的变化中,i到j的路线,是很有可能被改变的,而这种写法,后续是没法改掉的!
正确的应该是最外层是k循环(中间节点),内两层是i,j循环(路线【i到j】),这样才能保证路径一定能被发现,并且后续【i到j】的路径也能会应变,直到全部循环结束而被确立下来~
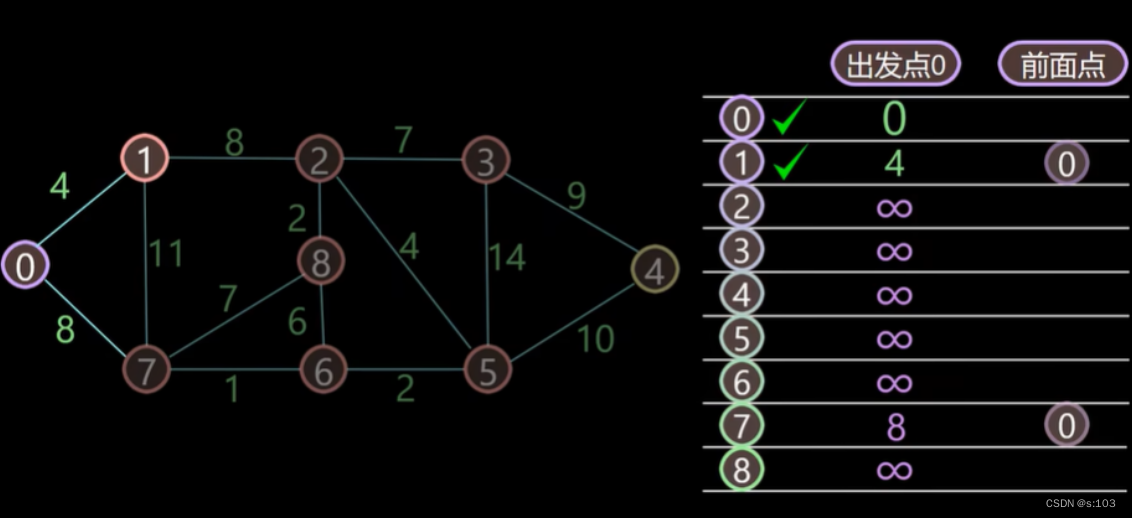
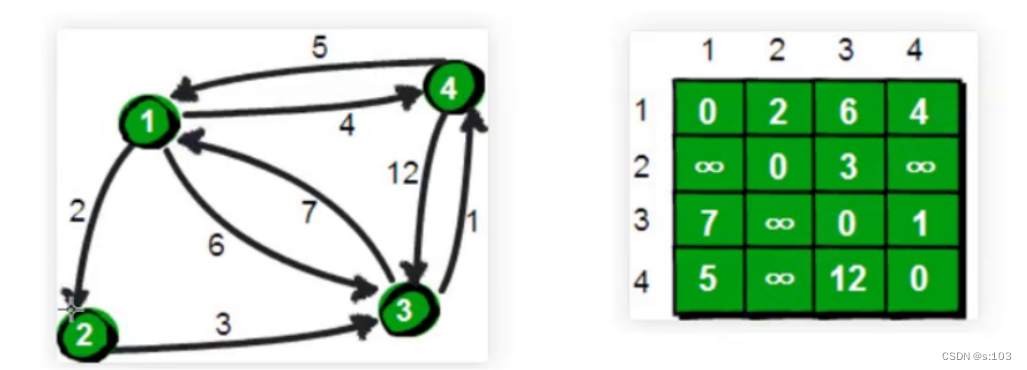
定义:
左图为:一个连通图
右图为:它的dist二维数组(初始状态,未开始算法)
- 定义一个dist二维数组,(i, j)代表这i到j的最短路径路径长
- 定义一个path二维数组,(i, j)代表这个i到j的路径的上一个顶点
- 在这一行上跳动即可
- 为什么可以跳动,原因与以上一致
可见时间复杂度为:O(N3)
推荐:Ep.23 弗洛伊德Floyd-Warshall算法_哔哩哔哩_bilibili
3.2 代码实现
public void floydWarShall(int[][] dist, int[][] path) {
//初始化dist和path
int n = arrayV.length;
for (int i = 0; i < n; i++) {
Arrays.fill(dist[i], Integer.MAX_VALUE);
Arrays.fill(path[i], -1);
}
//每一个顶点的第一代子图,记录在dist和path中,现在局部的最短路径
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if(matrix[i][j] != Integer.MAX_VALUE) {
dist[i][j] = matrix[i][j];
path[i][j] = i;//这一行的上一个就是i
}else {
path[i][j] = -1;//不存在路径
}
if(i == j) {
dist[i][j] = 0;
path[i][j] = j;//跳回本身
}
}
}
//进行算法,每个顶点都当一回中介点
//每个顶点都被当做一次起始点,终点
//一个点即使起始点有时中介点又是终点,好像也无所谓
//只要满足那个方程!
//顺序完全没关系~
for (int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
//规定k代表的是中介点,i为起始点,j为终点
boolean flag = dist[i][k] != Integer.MAX_VALUE
&& dist[k][j] != Integer.MAX_VALUE
&& dist[i][k] + dist[k][j] < dist[i][j];
//取不取等无所谓,只是不同最短路径的区别罢了
if (flag) {
dist[i][j] = dist[i][k] + dist[k][j];
path[i][j] = path[k][j];//【i,j】以【k,j】为子路径
}
}
}
}
}
- i与j与k相等没有什么大碍
测试:
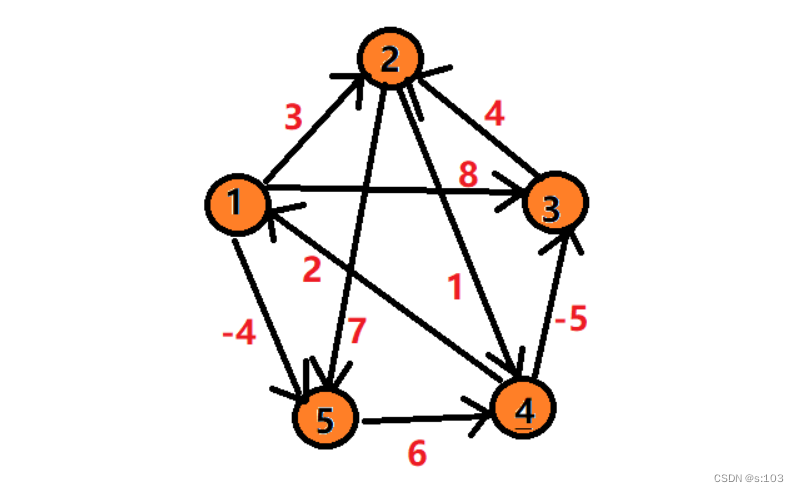
public static void testGraphFloydWarShall() {
String str = "12345";
char[] array = str.toCharArray();
GraphByMatrix g = new GraphByMatrix(str.length(),true);
g.initArrayV(array);
g.addEdge('1', '2', 3);
g.addEdge('1', '3', 8);
g.addEdge('1', '5', -4);
g.addEdge('2', '4', 1);
g.addEdge('2', '5', 7);
g.addEdge('3', '2', 4);
g.addEdge('4', '1', 2);
g.addEdge('4', '3', -5);
g.addEdge('5', '4', 6);
int[][] dist = new int[array.length][array.length];
int[][] path = new int[array.length][array.length];
g.floydWarShall(dist,path);
for (int i = 0; i < array.length; i++) {
g.printShortPath(array[i],dist[i],path[i]);
//把一行一行传过去~
//一行代表一个顶点到其他顶点的最短路径
}
}
public static void main(String[] args) {
testGraphFloydWarShall();
}

文章到此结束!谢谢观看
可以叫我 小马,我可能写的不好或者有错误,但是一起加油鸭?!这就是最短路径问题的全部内容了,如果有什么不懂可以留言/私信讨论!











 U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) Allegro16.6差分等长设置及走线总结
Allegro16.6差分等长设置及走线总结