队列 + 字典树 + 并查集 + 堆 + 哈希）网站首页 技术交流

ACM - 数据结构 - 基础（数组模拟链表 / 栈 / 队列 + 字典树 + 并查集 + 堆 + 哈希）

肆呀 2024-06-14 17:20:10

简介ACM - 数据结构 - 基础（数组模拟链表 / 栈 / 队列 + 字典树 + 并查集 + 堆 + 哈希）

数据结构

一、线性表
二、树型结构
三、集合
- 1、散列表 / 哈希表

一、线性表

1、单链表

模板题：AcWing 826. 单链表

原题链接：https://www.acwing.com/problem/content/828/

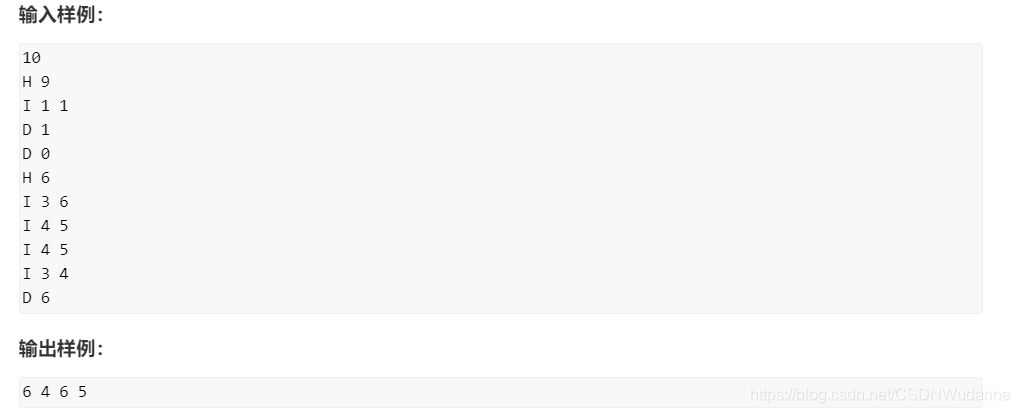
在这里插入图片描述

思路
数组模拟链表。
int e[ k ] ：第 k 个插入的结点的值
ne[ k ] ：第 k 个插入的结点的下一个结点的索引
idx ：表示目前已经插入过了多少个结点，包括remove过的结点数
head ：头指针

代码

#include <iostream>
#include <algorithm>
#include <iomanip>
#include <sstream>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <vector>
#include <map>
#include <set>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <climits>
#include <unordered_set>
#include <unordered_map>

using namespace std;

#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long 
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf

const int INF = 0x3f3f3f3f;
const int N = 100010; 

//(val & 1) == 0偶， == 1奇。
char op[5];

int e[N], ne[N], idx, head;

//初始化
void init() {
	idx = 1;
	head = 0;
	ne[head] = -1;  //用 -1 表示 null
}

//头插结点
void insert_to_head(int x) {
	e[idx] = x;
	ne[idx] = ne[head];
	ne[head] = idx ++;
} 

//移除第k个插入的数的后面的一个数
void remove(int k) {
	ne[k] = ne[ne[k]];
}

//在第 k 个插入的数后面插入 x 
void insert(int k, int x) {
	e[idx] = x;
	ne[idx] = ne[k];
	ne[k] = idx ++;
}

int main() {
	//freopen("D:\in.txt", "r", stdin); 
	//freopen("D:\out.txt", "w", stdout);
	init();
	rit;
	while (t --) {
		sc("%s", op);
		if (op[0] == 'H') {
			ria;
			insert_to_head(a);
		}
		else if (op[0] == 'D') {
			ria;
			remove(a);
		}
		else {
			rin;
			ria;
			insert(n, a);
		}
	}
	//从头到尾输出结点的值
	int k = ne[head];
	while (k != -1) {
		pr("%d ", e[k]);
		k = ne[k];
	}
	return 0;
}

2、双链表

模板题 AcWing 827. 双链表

原题链接：https://www.acwing.com/problem/content/829/
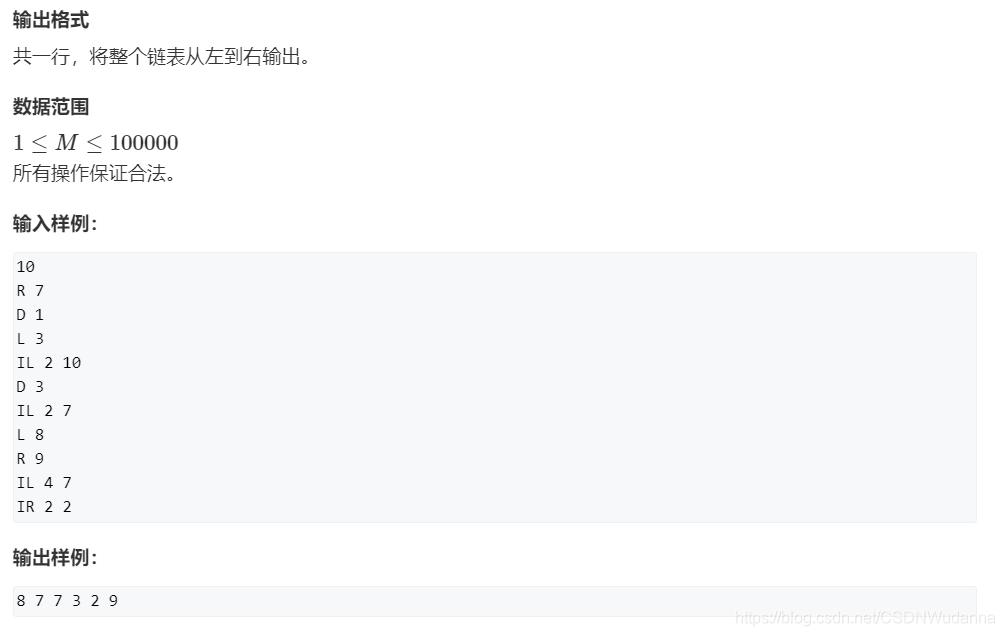
在这里插入图片描述

思路
e [ k ] ：idx = k 的值
l [ k ] ：idx = k 的左节点的索引
r [ k ] ：idx = k 的右节点的索引
idx ：idx = 0 表示左端点，idx = 1 表示右端点，idx 从 2 开始记录各个结点。

ps. 敲完一圈后会发现，每一次更改结点之间的指向时，如果要建的新节点在 k 的左边，那么新节点需要先和 k 的左节点建立联系，再去建立新节点和 k 的联系，反向也同理。

代码

#include <iostream>
#include <algorithm>
#include <iomanip>
#include <sstream>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <vector>
#include <map>
#include <set>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <climits>
#include <unordered_set>
#include <unordered_map>

using namespace std;

#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long 
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf

const int INF = 0x3f3f3f3f;
const int N = 100010; 
char op[5];
int e[N], l[N], r[N], idx;

//初始化
void init() {
	r[0] = 1;  //idx = 0 表示左端点，无值
	l[1] = 0;  //idx = 1 表示右端点，无值
	idx = 2;   //下标从2开始，所以对于输入数据的k需要自增1
}

//在双链表最左边插入值
void l_insert(int x) {
	e[idx] = x;
	r[idx] = r[0];
	l[r[0]] = idx;
	r[0] = idx;
	l[idx ++] = 0;
}

//在双链表最右边插入值
void r_insert(int x) {
	e[idx] = x;
	l[idx] = l[1];
	r[l[1]] = idx;
	r[idx] = 1;
	l[1] = idx ++;
}

//移除第 k 个加入双链表的结点
void remove(int k) {
	r[l[k]] = r[k];
	l[r[k]] = l[k];
}

//在第 k 个加入双链表的结点的左边增加结点
void l_insert_k(int k, int x) {
	e[idx] = x;
	l[idx] = l[k];
	r[l[k]] = idx;
	r[idx] = k;
	l[k] = idx ++;
}

//在第 k 个加入双链表的结点的右边增加结点
void r_insert_k(int k, int x) {
	e[idx] = x;
	r[idx] = r[k];
	l[r[k]] = idx;
	l[idx] = k;
	r[k] = idx ++;
} 


int main() {
	//freopen("D:\in.txt", "r", stdin); 
	//freopen("D:\out.txt", "w", stdout);
	init();
	rit;
	while (t --) {
		sc("%s", op);
		if (strlen(op) == 1) {
			ria;
			if (op[0] == 'L') l_insert(a);
			else if (op[0] == 'R') r_insert(a);
			else remove(a + 1);
		}
		else {
			rin;
			ria;
			if (op[1] == 'L') l_insert_k(n + 1, a);
			else r_insert_k(n + 1, a);
		}
	}
	//从头到尾输出结点的值 
	int k = r[0];
	while (k != 1) {
		pr("%d ", e[k]);
		k = r[k];
	}
	return 0;
}

3、栈

数组模拟栈模板 AcWing 828. 模拟栈

原题链接：https://www.acwing.com/problem/content/830/

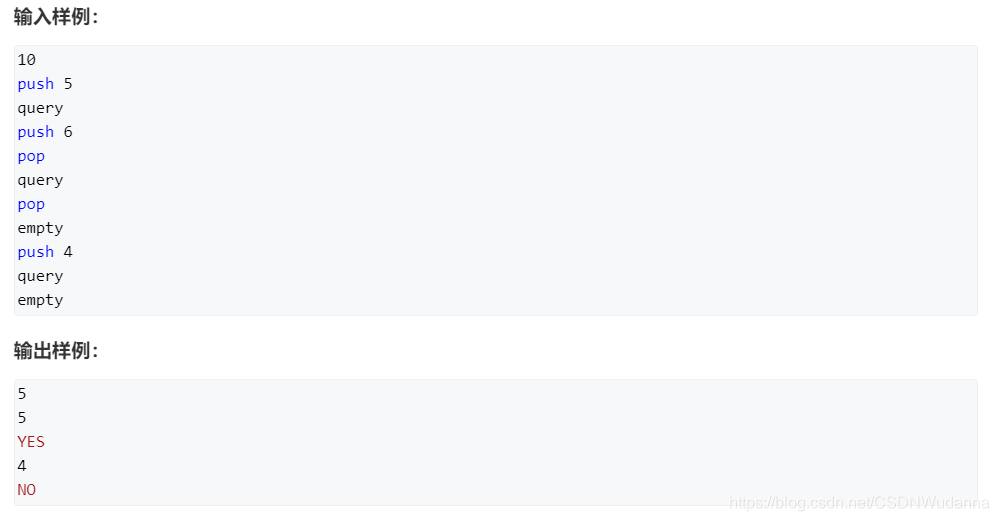
在这里插入图片描述

代码

// 也可以直接用vector直接模拟
//因为有size、pop_back、push_back这些函数。
#include <algorithm>
#include <iomanip>
#include <sstream>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <vector>
#include <map>
#include <set>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <climits>
#include <unordered_set>
#include <unordered_map>

using namespace std;

#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long 
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf

const int INF = 0x3f3f3f3f;
const int N = 100010; 

//(val & 1) == 0偶， == 1奇。
int st[N], tt;
char op[10];

void push(int x) {
	st[tt ++] = x;
}

void pop() {
	-- tt;
}

bool empty() {
	return tt == 0;
}

int query() {
	return st[tt - 1];
}

int main() {
	//freopen("D:\in.txt", "r", stdin); 
	//freopen("D:\out.txt", "w", stdout);
	rit;
	while (t --) {
		sc("%s", op);
		if (op[0] == 'e') {
			if(empty()) pr("YES
");
			else pr("NO
");
		}
		else if (op[0] == 'q') pr("%d
", query());
		else if (op[1] == 'o') pop();
		else {
			ria;
			push(a);
		}
	}
	return 0;
}

逆波兰简版模板

AcWing 3302. 表达式求值
原题链接：https://www.acwing.com/problem/content/description/3305/
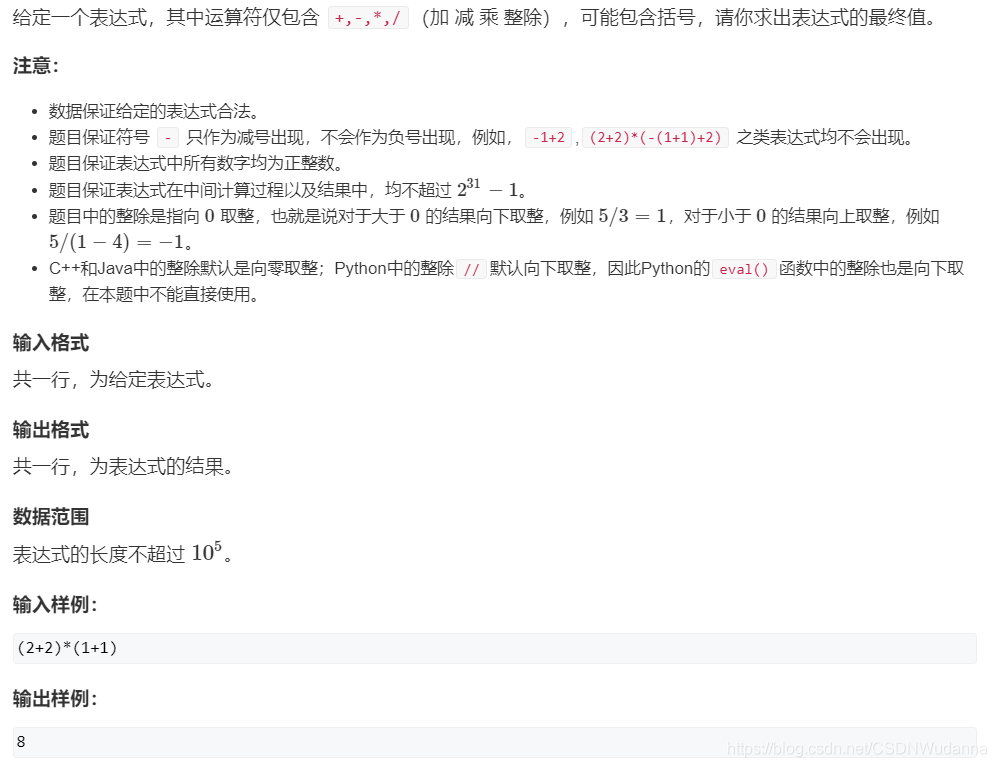
在这里插入图片描述

#include <bits/stdc++.h> 

using namespace std;

const int N = 100010; 

char str[N];
stack<int> num;
stack<char> op;  //符号栈

//判断是不是数字
bool isNum(char c) {
	return c <= '9' && c >= '0';
}

//计算当前的数
void count() {
	int b = num.top(); num.pop();
	int a = num.top(); num.pop();
	char c = op.top(); op.pop();
	if (c == '+') num.push(a + b);
	else if (c == '-') num.push(a - b);
	else if (c == '*') num.push(a * b);
	else num.push(a / b);
}

int main() {
	cin >> str;
	//设置优先级
	unordered_map<char, int> book = {{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}};
	int length = strlen(str);
	for (int i = 0; i < length; ++ i) {
		if (isNum(str[i])) {
			int a = 0, j = i;
			while (j < length && isNum(str[j])) {
				a = a * 10 + str[j] - '0';
				++ j;
			}
			num.push(a);
			i = j - 1;
		}
		else if (str[i] == '(') op.push(str[i]);
		else if (str[i] == ')') {
			while (op.top() != '(') {
				count();
			}
			op.pop();  //弹出左括号
		}
		else {
		    //优先级相等时也要从左到右算（主要是因为除法取整），所以需要包含等号
			while (!op.empty() && book[str[i]] <= book[op.top()]) {
				count();
			}
			op.push(str[i]);
		}
	} 
	while (!op.empty()) count();  //计算剩余的内容
	cout << num.top();
	return 0;
}

例题1、逆波兰表达式：HDU 1237 简单计算器（写得有点复杂）

原题链接：http://acm.hdu.edu.cn/showproblem.php?pid=1237

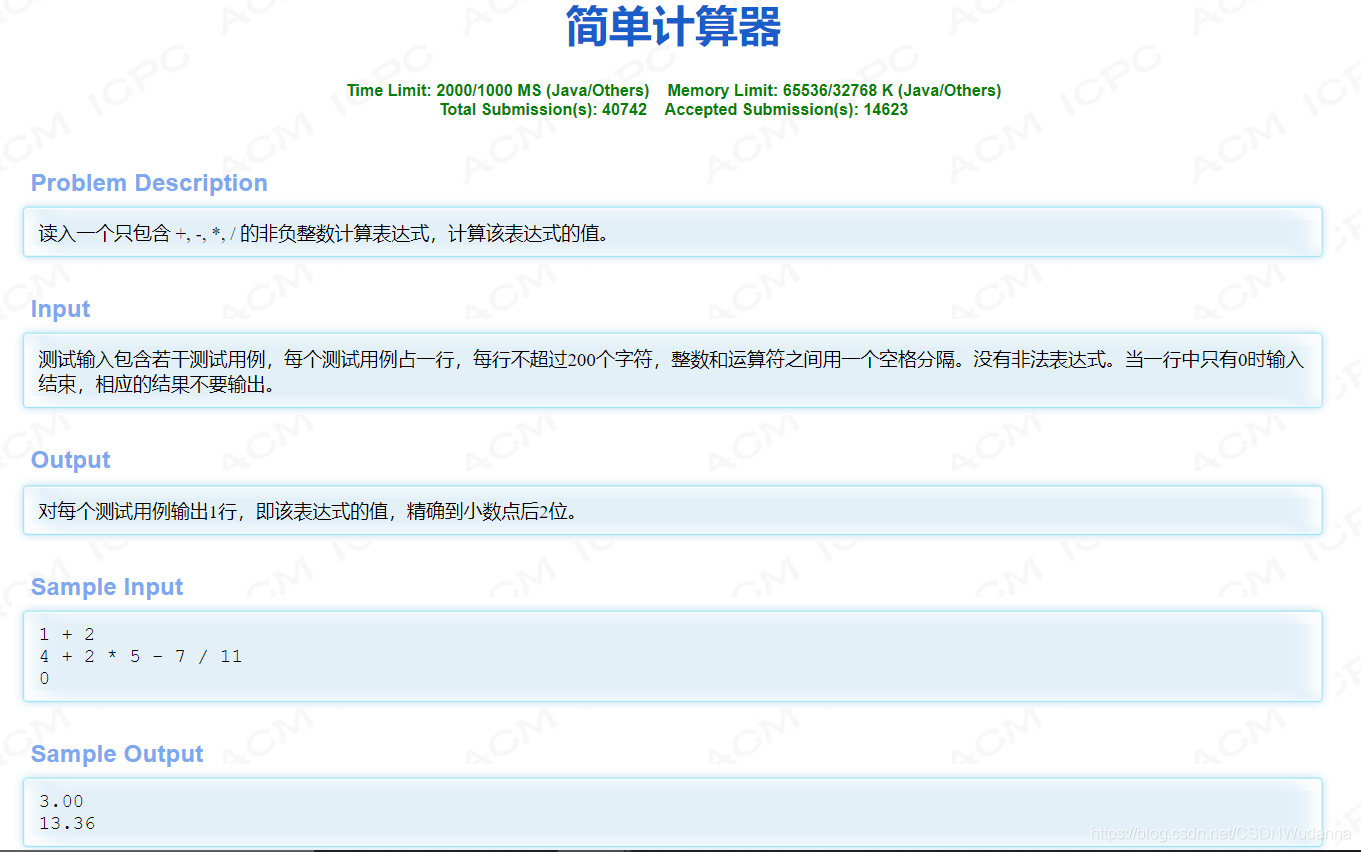
在这里插入图片描述
思路

对于表达式计算，我们可以先把中缀表达式转后缀表达式，然后直接计算。
当然这期间需要对暂时没用到的运算符压栈，轮到它了再取出来。
举个例子，对于 4 + 7 - 5 * 4 / 2 这样的表达式，不难得出其后缀表达式为：4 7 + 5 4 * 2 / -，在模拟的过程我们可以发现，对于运算符，如果栈为空或者当前的运算符优先级大于栈顶的运算符，那么直接压栈，反之一直出栈到不符合出栈规则，再把当前遇到的运算符入栈。

同时，为了方便，当一个运算符出栈时，直接对 ans 里面最后的两个元素进行计算，就不用在转后缀后还要从头走到尾。
比如说一开始 ans 里面只有 4 和 7，那么当 + 出栈的时候，直接将 4 和 7 从 ans 里面弹出，将计算出来的 11 放入 ans 里面。

ps.这里有一个很玄学的地方，就是我用下面的代码，在本地能跑出正确结果，用 G++ 交也能 AC，但是用 C++ 交就莫名其妙的 CE 了，一直想不通为什么 C++ 会报编译错，如果有了解原因的大佬，希望能不吝赐教 ~
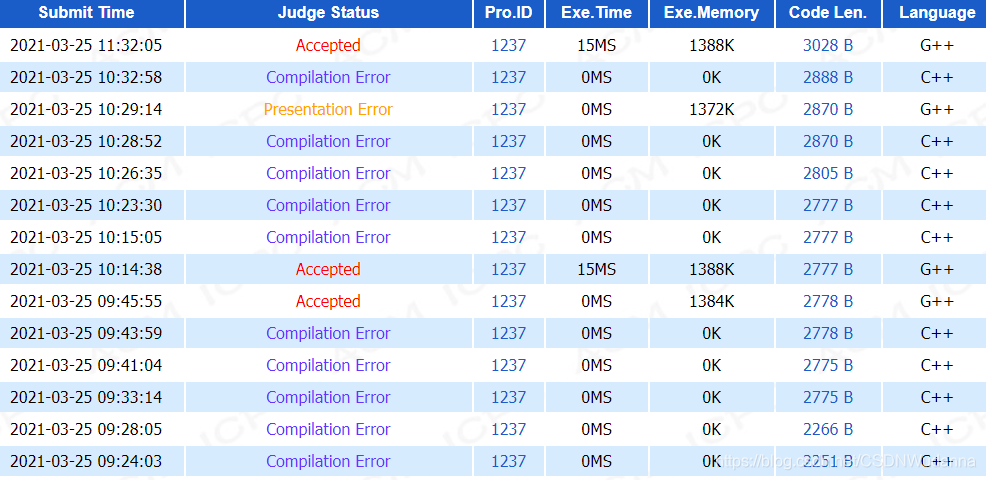
在这里插入图片描述

代码

#include <iostream>
#include <algorithm>
#include <iomanip>
#include <sstream>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <vector>
#include <map>
#include <set>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <climits>
#include <unordered_set>
#include <unordered_map>

using namespace std;

#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long 
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf

const int INF = 0x3f3f3f3f;
const int N = 300; 

char sign_stack[N];  //符号栈
int  tt, aa;  // tt - 符号栈的栈顶索引，aa -- ans数组的栈顶索引
double ans[N];  //计算的最终结果
char str[210];  //读入的表达式

//初始化
void init() {
    tt = 0;
    aa = 0;
}

//符号栈的压栈
void push(char x) {
    sign_stack[tt ++] = x;
}

//符号栈的出栈
void pop() {
    -- tt;
}

//对符号栈判空
bool empty() {
    return tt == 0;
}

//返回符号栈栈顶
char query() {
    return sign_stack[tt - 1];
}

bool isNum(char c) {
    return c >= '0' && c <= '9';
}

//判断是不是数字
int get_grade(char c) {
    if (c == '+' || c == '-') return 1;
    else return 2;
}

//计算 a 和 b的运算结果，c为运算符
double count(double a, double b, char c) {
    if (c == '+') return a + b;
    else if (c == '-') return a - b;
    else if (c == '*') return a * b;
    else return a / b;
}

int main() {
    //freopen("D:\in.txt", "r", stdin); 
    //freopen("D:\out.txt", "w", stdout);
    while (sc("%[^
]", str) != -1) {
        getchar();  //吸取回车键
        int length = strlen(str);
        if (length == 1 && str[0] == '0') break;
        init();
        for (int i = 0; i < length; ++ i) {
        	//数字
            if (isNum(str[i])) {
                double num = 0;
                while (isNum(str[i])) {
                    num = num * 10 + str[i ++] - '0';
                }
                ans[aa ++] = num;
            }
            //运算符
            else {
                int b = get_grade(str[i]);  //获得优先级
                if (empty() || get_grade(query()) < b) {
                    push(str[i]);    
                }
                else {
                    while (!empty() && (b == get_grade(query()) || b < get_grade(query()))) {
                        double a, b;
                        b = ans[aa - 1], a = ans[aa - 2];
                        aa -= 2;
                        ans[aa ++] = count(a, b, query()) ;  //计算
                        pop();    
                    }
                    push(str[i]);
                }
                ++ i;
            }
        }
        //符号栈不为空
        while (!empty()) {
            double a, b;
            b = ans[aa - 1], a = ans[aa - 2];
            aa -= 2;
            ans[aa ++] = count(a, b, query()) ;
            pop();    
        }
        pr("%.2lf
", ans[0]);
    }
    return 0;
}

4、队列

数组模拟队列模板题 AcWing 829. 模拟队列

原题链接：https://www.acwing.com/problem/content/831/
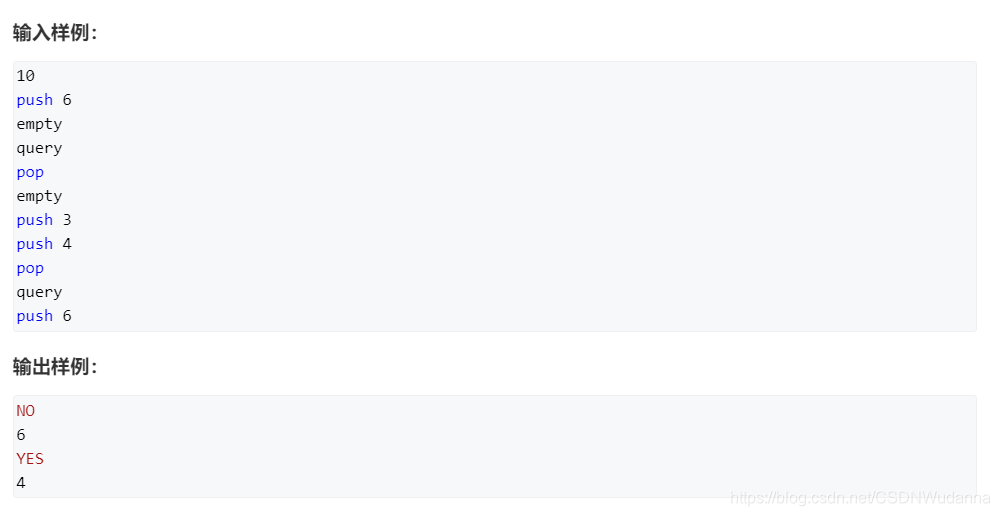
在这里插入图片描述

代码

#include <iostream>
#include <algorithm>
#include <iomanip>
#include <sstream>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <vector>
#include <map>
#include <set>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <climits>
#include <unordered_set>
#include <unordered_map>

using namespace std;

#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long 
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf

const int INF = 0x3f3f3f3f;
const int N = 100010; 

//(val & 1) == 0偶， == 1奇。

int que[N];
int hh, tt;  // hh-队头，tt-队尾
char op[10];

void init() {
	hh = 0;
	tt = 0;
}

void push(int x) {
	que[tt ++] = x;
}

void pop() {
	++ hh;
}

bool empty() {
	return hh == tt;
}

int query() {
	return que[hh];
}
 
int main() {
	//freopen("D:\in.txt", "r", stdin);
	//freopen("D:\out.txt", "w", stdout);
	rit;
	init();
	while (t --) {
		sc("%s", op);
		if (op[0] == 'q') pr("%d
", query());
		else if (op[0] == 'e')  {
			if (empty()) pr("YES
");
			else pr("NO
");
		}
		else if (op[1] == 'o') pop();
		else {
			ria;
			push(a);
		}
	}
	return 0;
}

5、单调栈 / 单调队列

传送门：单调栈 / 单调队列

一般单调栈适用于求在某一个元素最左边 / 最右边第一个比它大 / 小（或者最大 / 最小）的问题；
而单调队列一般适用于类似滑动窗口的问题。

简而言之，所谓的单调栈单调队列是为了维护某一个单调不增 / 单调递增 / 单调不减 / 单调递减区间，起辅助作用。

构造单峰数列

AcWing 3780. 构造数组

原题链接：https://www.acwing.com/problem/content/description/3783/
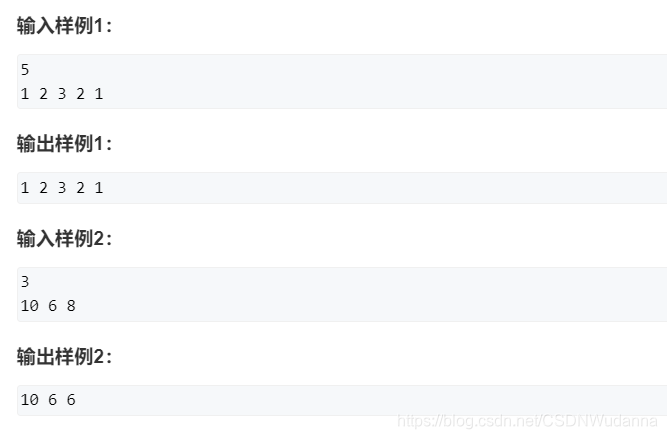
在这里插入图片描述

/*
若将数组按照大小画成曲线图，不存在 aj > ai < ak 意味着不会有凹的情况。
换而言之不会有双峰，那么就只有单峰或者单调递增/减。
设L[i]表示以 i 为峰值，i 的左边能达到的最大值。
设 v 为 i 左边第一个比 i 小的数，则可得出 L[i] = L[v] + (i - v) * nums[i]。
同理可以求得右边，那么从 1 到 n 枚举 L[i] + R[i] - nums[i] 即可在O(n)复杂度完成。

当然，本题还需要用的单调栈获得每一个数左边（右边）第一个比他小的数，综上可解。
*/

#include<bits/stdc++.h>

using namespace std;

const int N = 500010;

long long nums[N], l[N], r[N], ans[N];

struct node{
	int idx, val;
};

int main() {
	int n;
	cin >> n;
	nums[0] = 0;
	//求左边
	stack<node> s;
	s.push({0, 0});
	for (int i = 1; i <= n; ++ i) {
		cin >> nums[i];
		while (!s.empty() && s.top().val >= nums[i]) s.pop();
		int idx = s.top().idx;
		l[i] = l[idx] + (i - idx) * nums[i];
		s.push({i, nums[i]});
	}
	//求右边
	stack<node> st;
	st.push({n + 1, 0});
	for (int i = n; i >= 1; -- i) {
		while (!st.empty() && st.top().val >= nums[i]) st.pop();
		int idx = st.top().idx;
		r[i] = r[idx] + (idx - i) * nums[i];
		st.push({i, nums[i]});
	}
	//枚举峰值
	long long maxx = 0, idx = 0;
	for (int i = 1; i <= n; ++ i) {
		if (l[i] + r[i + 1] > maxx) {
			maxx = l[i] + r[i] - nums[i];
			idx = i;
		}
	}
	//输出
	ans[idx] = nums[idx];
	for (int i = idx - 1, j = idx + 1; i >= 1 || j <= n; -- i, ++ j) {
		if (i >= 1) ans[i] = min(nums[i], ans[i + 1]);
		if (j <= n) ans[j] = min(nums[j], ans[j - 1]);
	}
	for (int i = 1; i <= n; ++ i) cout << ans[i] << " ";
	return 0;
}

二、树型结构

1、字典树 Trie

模板题 AcWing 835. Trie字符串统计

原题链接：https://www.acwing.com/problem/content/submission/code_detail/4656752/

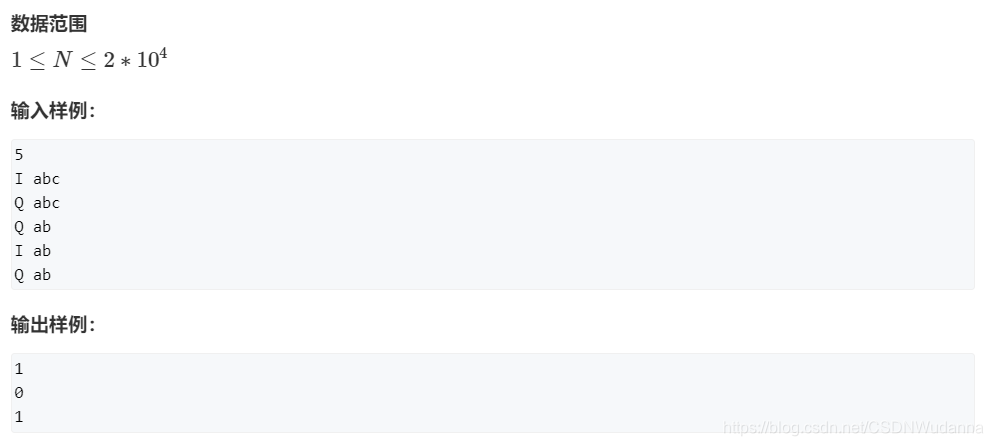
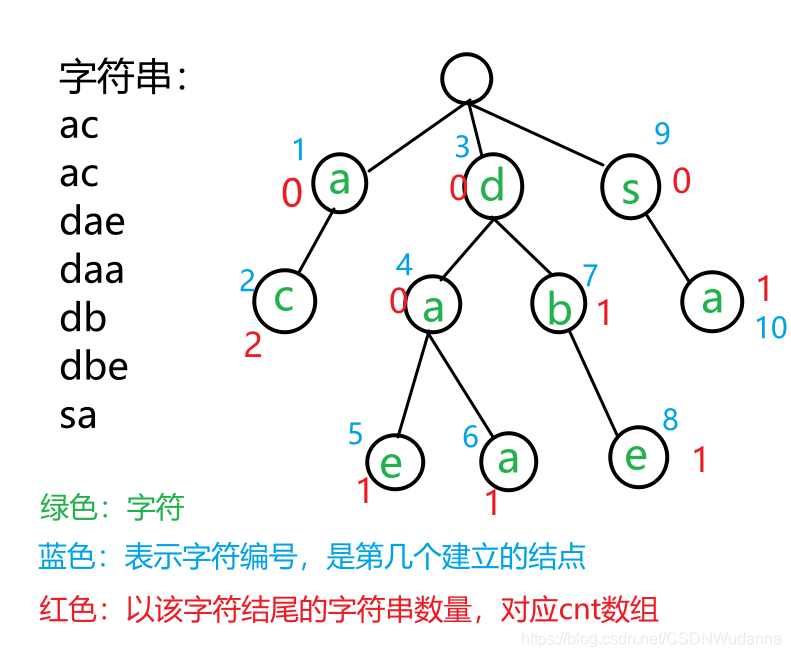
在这里插入图片描述

变量含义解释

idx 表示此时如果要增加结点，那么这个结点的编号为idx（之所以 idx 从 0 开始是因为数组初始化为 0 ，所以结点编号得从 1 开始）；
son [ i ] [ j ] 表示编号为 i 号的结点的（‘ a ’ + j ）字符的子节点的编号，如果 son [ i ] [ j ] == 0，说明该子节点不存在；
cnt [ i ] 表示以编号为 i 的结点为尾字符的字符串有多少个，或者说从树根到 i 号结点构成的字符串有多少个。
在这里插入图片描述

代码

#include<iostream>
using namespace std;

const int N = 100010;

int cnt[N], son[N][26], idx = 1;
char op[5], str[N];

void insert(char *str) {
    int p = 0;
    for (int i = 0; str[i]; ++ i) {
        int u = str[i] - 'a';
        if (son[p][u] == 0) son[p][u] = idx ++;
        p = son[p][u];
    }
    ++ cnt[p];
}

int query(char *str) {
    int p = 0;
    for (int i = 0; str[i]; ++ i) {
        int u = str[i] - 'a';
        if (son[p][u] == 0) return 0;
        p = son[p][u];
    }
    return cnt[p];
}


int main() {
    int t;
    scanf("%d", &t);
    while (t --) {
        scanf("%s%s", op, str);
        if (op[0] == 'I') insert(str);
        else printf("%d
", query(str));
    }
    return 0;
}

例题1、二进制字典树：AcWing 143. 最大异或对

原题链接：https://www.acwing.com/problem/content/description/145/
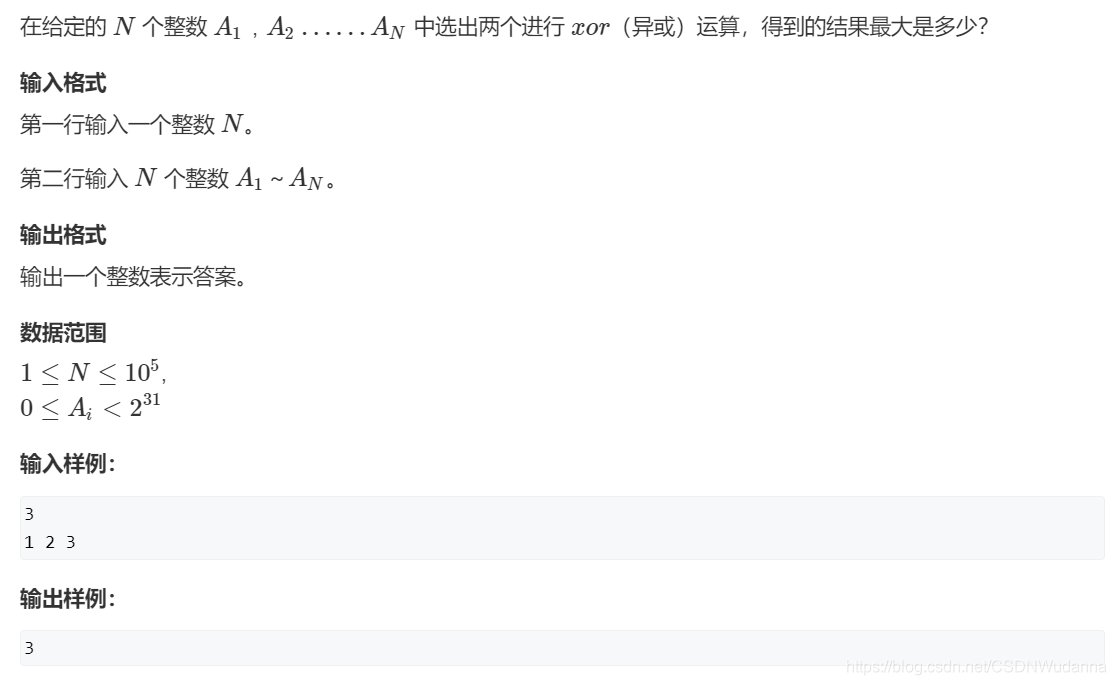
在这里插入图片描述
思路

一开始想着递归进去直接一次性找到最大异或对，如果能走01就走01，不能再退而求其次走00或者11，但是可能在回溯的时候临时数组没处理好，有一个样例一直过不去，后面就看了题解，发现其实可以直接拿每一个数去字典树找最大异或对，代码难度就小了很多，而且因为 a ^ b = b ^ a，所以并不需要整棵字典树建好再查最大异或对，每新插入一个二进制数，就查一下它和当前字典树的最大异或对，这样就能保证不重不漏。

代码

#include<iostream>
using namespace std;

const int N = 100010 * 32;  //每一个数需要存下31位二进制数

int son[N][2], idx = 1;

void insert(int a) {
    int p = 0;
    for (int i = 30; i >= 0; -- i) {
        int u = (a >> i) & 1;
        if (!son[p][u]) son[p][u] = idx ++;
        p = son[p][u];
    }
}

int query(int a) {
    int p = 0, res = 0;
    for (int i = 30; i >= 0; -- i) {
        int u = (a >> i) & 1;
        res <<= 1;
        if (son[p][!u]) { //和a的第i位不同的数
            p = son[p][!u];
            res += 1;
        } 
        else {
            p = son[p][u];
        }
    }
    return res;
}

int main() {
    int n, ans = 0;
    scanf("%d", &n);
    while (n --) {
        int a;
        scanf("%d", &a);
        insert(a);
        ans = max(ans, query(a));
    }
    printf("%d
", ans);
}

2、并查集

模板题 AcWing 836. 合并集合

原题链接：https://www.acwing.com/problem/content/description/838/

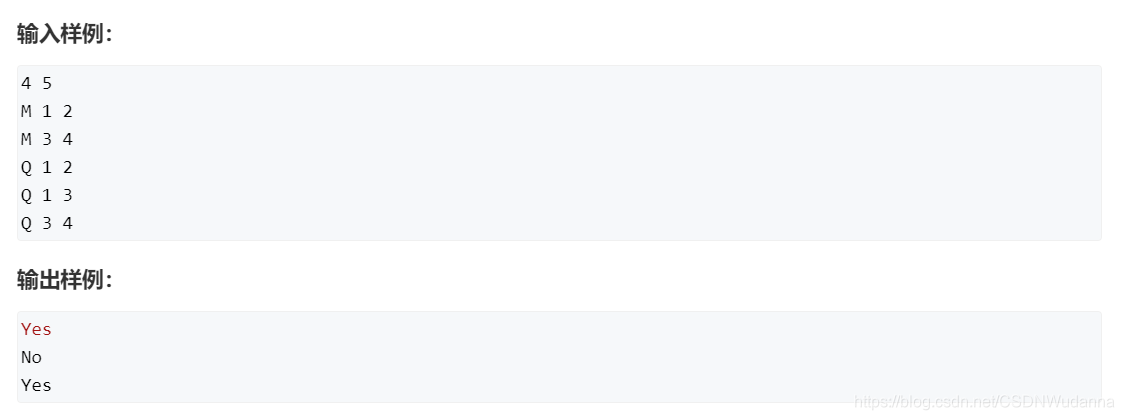
在这里插入图片描述

思路
n 个结点从 1 开始编号到 n ，一开始每一个结点的父节点是虚设的，每一个结点也相当于一个独立的集合，此时 father [ x ] = x 。当需要合并两个集合的时候，我们把其中一个集合的根节点插入到另一个集合的根节点下，这样这两个集合就有了共同的祖先。

降低数的高度：每 find 一次，就让子孙结点提升辈分到根节点的子节点。
（使得查询时时间复杂度类 O (1) ）

代码

#include<iostream>
using namespace std;

const int N = 100010;

int father[N];  // 存每个结点的父结点
char op[3];

int find (int x) {
    if (father[x] != x) 
    	return father[x] = find(father[x]); //对father[x]重新赋值，以降低树的高度
    return x;
}

int main() {
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++ i) father[i] = i;
    while (m --){
        int a, b;
        scanf("%s%d%d", op, &a, &b);
        if (op[0] == 'M') father[find(a)] = find(b); //根节点变成另一个根结点的子节点
        else {
            if (find(a) == find(b)) printf("Yes
");
            else printf("No
");
        }
    }
    return 0;
}

单链表并查集 : AcWing 1242. 修改数组

原题链接:https://www.acwing.com/problem/content/1244/

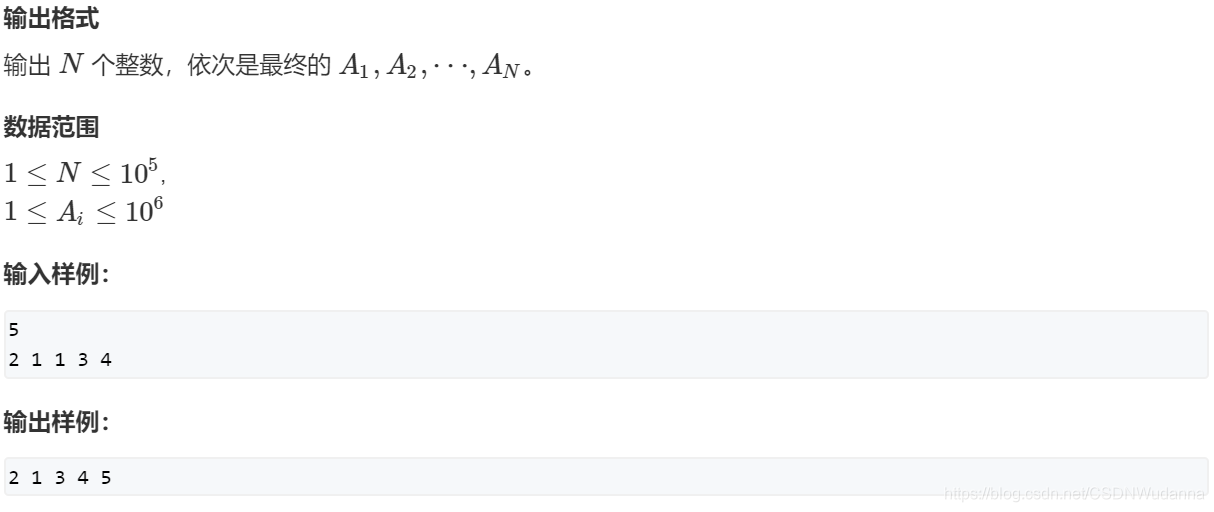
在这里插入图片描述

思路

(有生之年–单链表并查集)

ne[a]表示假如如果遇到数a,那么nums的当前位置应该是ne[a]才不会和前面的数字重复.
用并查集维护根(根 == 每一个位置应该放的不会和前面重复的数)

局限性: a 的数值不能过大

#include<iostream>
#include <algorithm>

using namespace std;

const int N = 1000010;

int nums[N], ne[N];

int find(int a) {
	if (ne[a] == a) {
		++ ne[a];
		return a;
	}
	else {
		ne[a] = find(ne[a]);
		return ne[a];
	}
} 

int main() {
	int n;
	scanf("%d", &n);
	for (int i = 1; i < N; ++ i) ne[i] = i;
	for (int i = 0; i < n; ++ i) {
		int a;
		scanf("%d", &a);
		printf("%d ", find(a));
	}
}

根节点维护连通块结点数：AcWing 837. 连通块中点的数量

原题链接：https://www.acwing.com/problem/content/839/

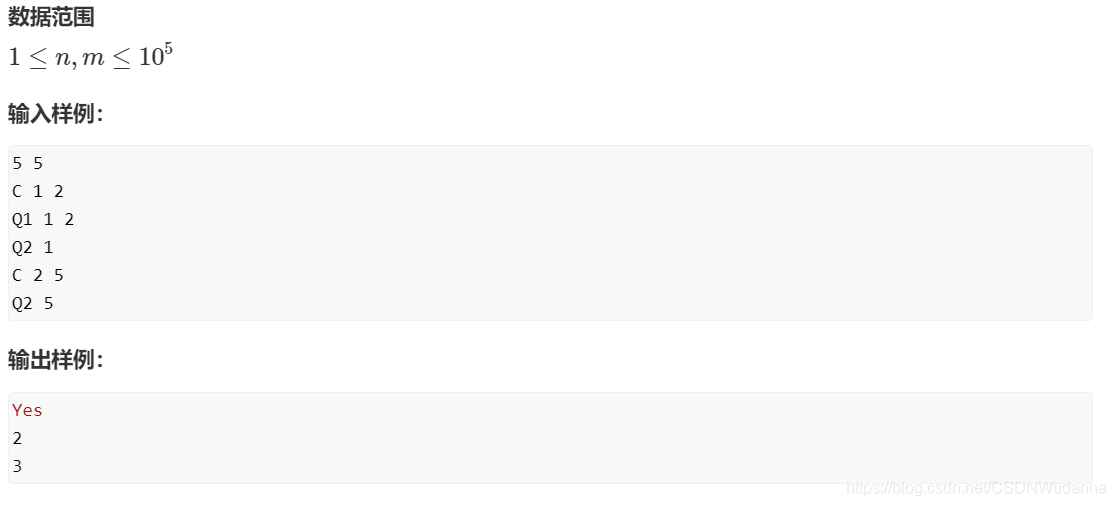
在这里插入图片描述

思路

对于每一个集合的根节点先初始化为 -1，表示此时集合有 abs（-1）个结点。
每一次合并集合时，更新 father [ 根节点 ] = - 根节点所在集合的节点数量
即：
以数组元素的正负判断是否为根节点；
以根节点的数组元素值的绝对值表示该集合的结点数量。

代码

#include<iostream>
using namespace std;

const int N = 100010;

int father[N];
char op[3];

int find (int x) {
    if (father[x] >= 0) return father[x] = find(father[x]);
    return x;
}

int main() {
    int n, m, a, b;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++ i) father[i] = -1;
    while (m --) {
        scanf("%s", op);
        //连接两个点
        if (op[0] == 'C') {
            scanf("%d%d", &a, &b);
            int x = find(a), y = find(b);
            if (x != y) {
                father[y] += father[x];  //合并时，要增加集合的结点数
                father[x] = y; // 让其中一个根节点成为另一个根节点的子节点
            }
        }
        //查询是否在同一个集合
        else if (op[1] == '1') {
            scanf("%d%d", &a, &b);
            if (find(a) == find(b)) printf("Yes
");
            else printf("No
");
        }
        //返回该点所在集合的结点数量
        else {
            scanf("%d", &a);
            printf("%d
", abs(father[find(a)]));
        }
    }
    return 0;
}

额外维护每一个结点到根节点的距离：AcWing 240. 食物链

原题链接：https://www.acwing.com/problem/content/description/242/
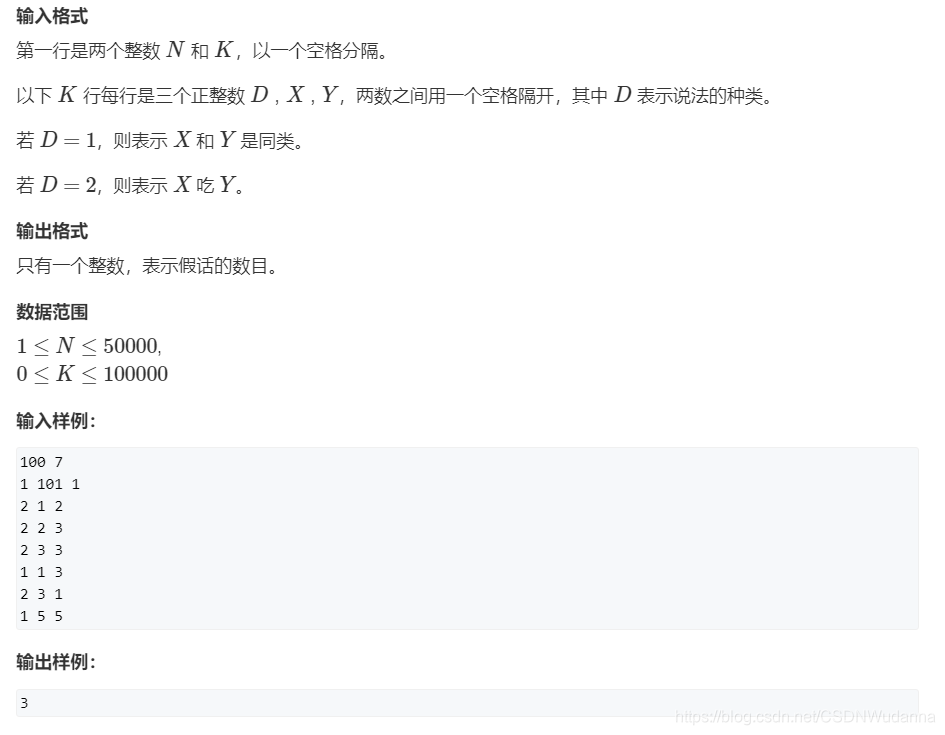
在这里插入图片描述

思路
因为题目明确表明只有三种动物，所以我们可以在 % 3 的意义下构造出这么一个并查集：

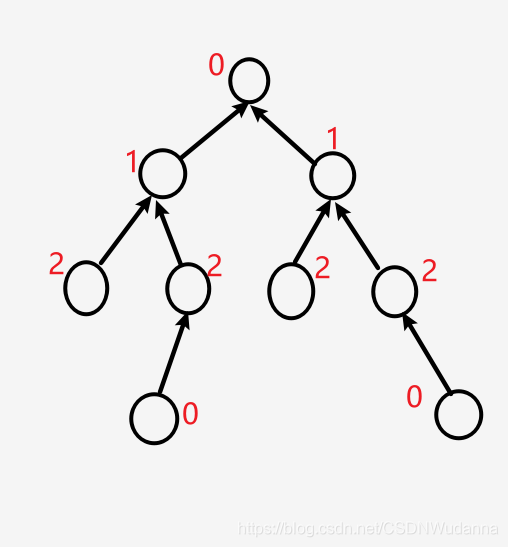
dis 数组维护的是：第一层结点到根节点的距离为0，第二层为 1 ，第三层为 2，第四层为 0（因为 3 % 3 == 0），……
在 % 3 意义下，如果 dis[ 第 x 层 ] - dis [第 y 层 ] - 1 == 0，表示 y 被 x 吃，即：上图的第二层吃第一层，第三层吃第二层，第四层吃第三层且第四层和第一层是同类。

如此，我们就可以用一个并查集记录某一批动物之间关系的连通块，以快速查找当次查询中，x 动物和 y 动物是否已经建立好彼此的关系再去判断是真话假话。

而 dis 数组则存下每一个点到根节点的距离，换而言之就是存下了每一个点和根节点是吃、被吃还是同类的关系。

当然，以上只是 father、dis 数组的意义介绍，更为抽象的是如何用代码记录和修改关系。

首先，如果在 x 和 y 动物编号合法（不会大于 n ，也不会 x == y）的前提下，
① 假如 x 和 y 的关系已经记录在同一个集合里面，那么在 % 3 意义下，假如 d == 1，则 dis [ x ] == dis [ y ] 才能说明两者是同类；如果 d == 2，那么 dis [ x ] - 1 = dis [ y ] 才能说明两者是 x 吃 y 的关系。

② 假如 x 和 y 的是记录在互相独立的集合里面，那么此时只需要更新集合的关系，不需要判断真假话（因为不会和前面的话冲突）。

首先很明显，如果一改，那么必然是要其中一个集合的 dis 整个改掉，显然有些繁琐，但是如果我们只改根节点，在每一次进行查询真假话前，都会 int fx = find(x), fy = find(y); 我们可以借助 find 函数本身的递归过程使得沿线的需要用到的结点在 find 的时候自动改掉，而不用我们额外修改。

因为如果原先 dis [ 根节点 ] = a，当其变化了 b 时，因为是 % 3 意义下的操作，所以后续的结点相当于也只需要跟着变化 b 即可。

（此外，因为每一次 find 都是直接让沿途的结点直接指向根节点，换句话说这些结点的父节点直接是根节点，那么 dis[x] += dis[father[x]]; 的时候就不会多加累加，因为每一个结点只会加上根节点的dis，由此可证这里的操作是合法的）

那么合并两个集合的核心代码如下：

int fx = find(x), fy = find(y);

if (d == 1 && fx != fy) {
	father[fx] = fy;
	dis[fx] = dis[y] - dis[x]; // 因为x和y是同类，并且要消去原先x的dis的影响
}

if (d == 2 && fx != fy) {
	father[fx] = fy; 
    dis[fx] = dis[y] + 1 - dis[x]; // 因为是x吃y，所以需要再 +1，并且要消去原先x的dis的影响
}

代码

#include<iostream>

using namespace std;

const int N = 50100;

int father[N], dis[N];

int find(int x) {
    if (father[x] != x) {
        int temp = find(father[x]);
        dis[x] += dis[father[x]];
        father[x] = temp;
    }
    return father[x];
}

int main() {
    int n, k;
    scanf("%d%d", &n, &k);
    for (int i = 1; i <= n; ++ i) father[i] = i;
    int ans = 0, d, x, y;
    while (k --) {
        scanf("%d%d%d", &d, &x, &y);
        if (x > n || y > n) ++ ans;
        else {
            int fx = find(x), fy = find(y);
            if (d == 1) {
                if (fx == fy) {
                    if ((dis[x] - dis[y]) % 3 != 0) ++ ans;
                }
                else {
                    father[fx] = fy;
                    dis[fx] = dis[y] - dis[x];
                }
            }
            else {
                if (x == y) ++ ans;
                else {
                    if (fx == fy) {
                        if ((dis[x] - dis[y] - 1) % 3 != 0) ++ ans;
                    }
                    else {
                        father[fx] = fy;
                        dis[fx] = dis[y] + 1 - dis[x];
                    }
                }
            }
        }
    }
    printf("%d
", ans);
    return 0;
}

3、堆 / 优先队列

堆排序： AcWing 838. 堆排序

原题链接：https://www.acwing.com/problem/content/description/840/

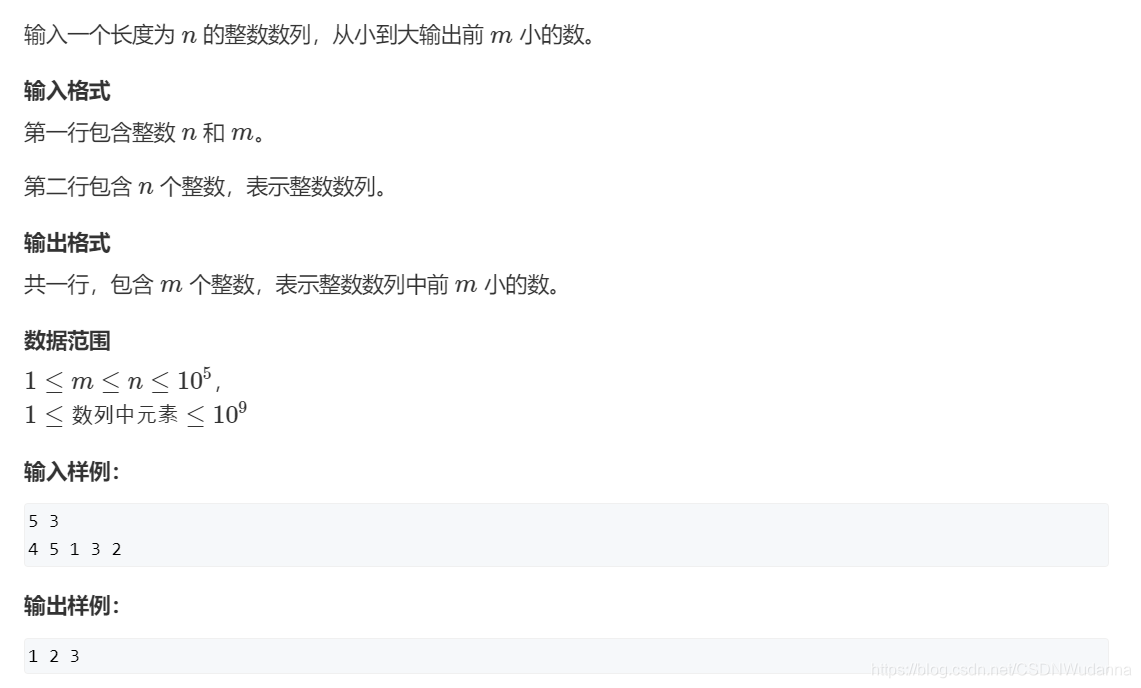
在这里插入图片描述
思路
需要注意的是，每一次取出堆顶，都要更新一下再down一下，因为堆只能保证堆顶一定是最值，至于第二层是不是都比第三层到最后一层大（或小）是不保证的。

代码

#include<iostream>

using namespace std;

const int N = 100010;

int nums[N];
int n, m;

void down(int a) {
    int b = a;
    if (a * 2 <= n && nums[a * 2] < nums[b]) b = a * 2;
    if (a * 2 + 1 <= n && nums[a * 2 + 1] < nums[b]) b = a * 2 + 1;
    if (a != b) {
        swap(nums[a], nums[b]);
        down(b);
    }
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++ i) scanf("%d", &nums[i]);
    for (int i = n / 2; i; -- i) down(i);
    while (m --) {
        printf("%d ", nums[1]);
        nums[1] = nums[n --];
        down(1);
    }
    return 0;
}

维护前 m 个数：HDU 1280 前m大的数

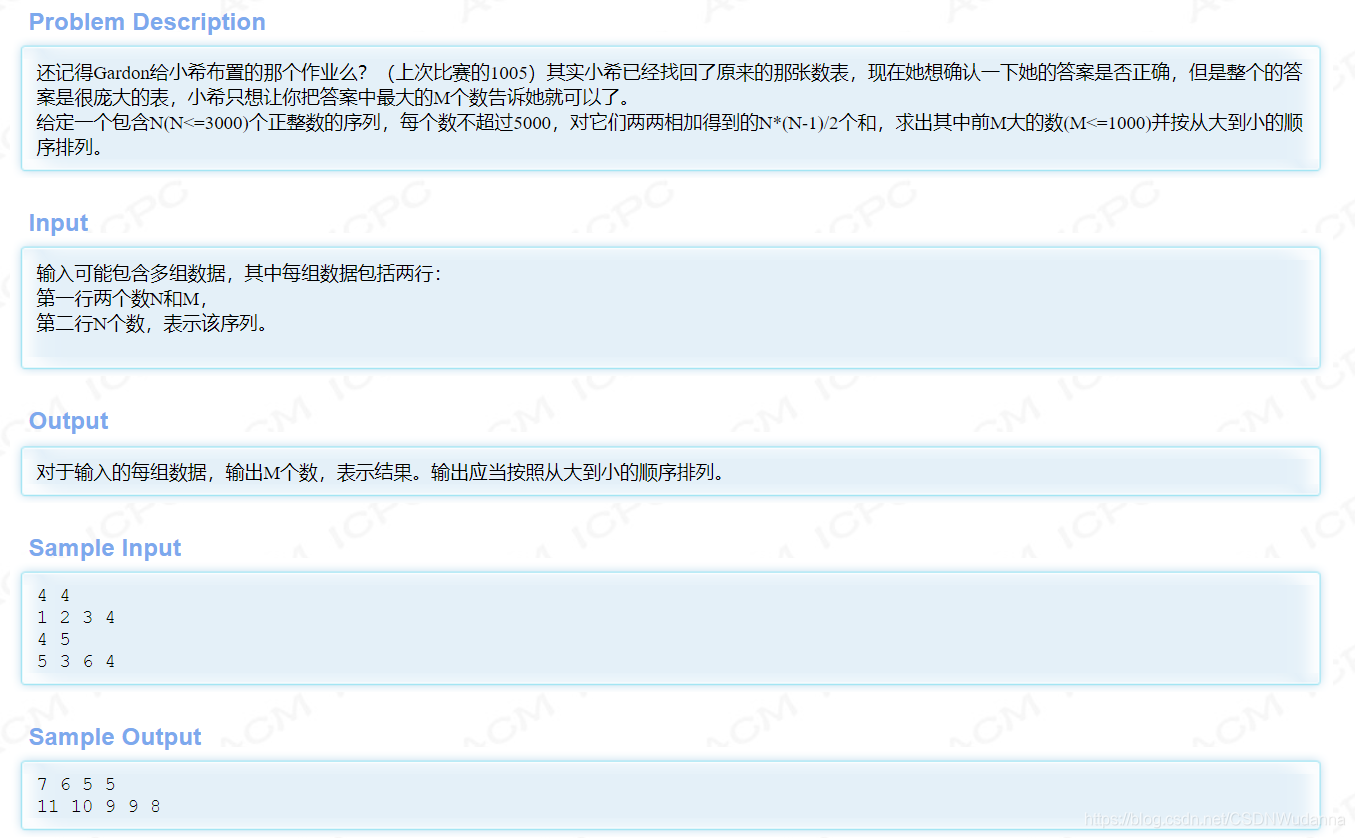
在这里插入图片描述

思路
这道题首先，不能直接把 (n - 1) * n / 2 个数全部放在堆里面，不然会超时，对于heap直接维护 m 个数就好了，等这 (n - 1) * n / 2 个数全部过一遍后，heap里面剩下的数就是满足要求的前 m 个数。

还要注意的是，输出的时候每一行末尾不能有空格，否则会PE。

代码

#include <iostream>
#include <algorithm>
#include <iomanip>
#include <sstream>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <vector>
#include <map>
#include <set>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <climits>
#include <unordered_set>
#include <unordered_map>

using namespace std;

#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long 
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf

const int INF = 0x3f3f3f3f;
const int N = 4000, M = 1010; 

int nums[N], heap[M], ans[M];  
int n, m;

void down(int a) {
	int b = a;
	if (a * 2 <= m && heap[b] > heap[a * 2]) b = a * 2;
	if (a * 2 + 1 <= m && heap[b] > heap[a * 2 + 1]) b = a * 2 + 1;
	if (a != b) {
		swap(heap[a], heap[b]);
		down(b);
	}
}

int main() {
	freopen("D:\in.txt", "r", stdin); 
	//freopen("D:\out.txt", "w", stdout);
	
	while(sc("%d%d", &n, &m) != -1 ) {
		//输入数
		for (int i = 0; i < n; ++ i) {
			sc("%d", &nums[i]);
		}
		//维护前 m 个数
		MEM(heap, 0);
		int cnt = 0, i, j;
		for (i = 0; i < n - 1; ++ i) {
			for (j = i + 1; j < n; ++ j) {
				int num = nums[i] + nums[j];
				++ cnt;
				if (cnt < m) {
					heap[cnt] = num;
				}
				else if (cnt == m) {
					heap[cnt] = num;
					for (int p = m / 2; p > 0; -- p) down(p);
				}
				else {
					if (num > heap[1]) {
						heap[1] = num;
						down(1);
					}
				}
			}
		}
		//获得ans数组
		cnt = m;
		for (int i = 1; i <= cnt; ++ i) {
			ans[i] = heap[1];
			heap[1] = heap[m --];
			down(1);
		}
		for (int i = cnt; i >= 2; -- i) pr("%d ", ans[i]);
		pr("%d", ans[1]);
		pr("
");
	}
	
	return 0;
}

堆的增删改查：AcWing 839. 模拟堆

原题链接：https://www.acwing.com/problem/content/description/841/
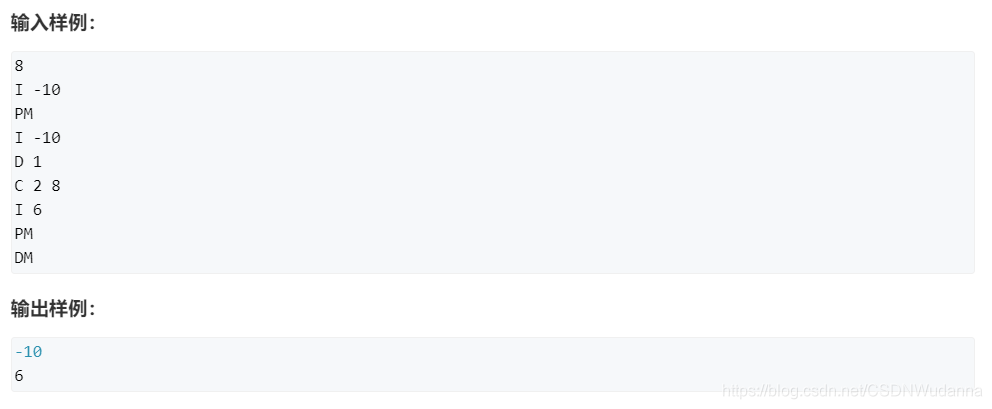
在这里插入图片描述

变量解释

int heap[N], hp[N], ph[N], idx = 1, cnt = 0;

heap : 堆
hp ：heap point to idx, hp[1] = 6 表示堆的第1个数是第6个插入的数
ph : idx point to heap, ph[1] = 6 表示第1个插入的数在堆的第6个位置
idx : 第几个插入的数
cnt : 当前堆有cnt个数

代码

#include<iostream>
#include<cstring>
#include<string>

using namespace std;

const int N = 100010;

int heap[N], hp[N], ph[N], idx = 1, cnt = 0;
char op[6];

//交换操作
void heap_swap(int a, int b) {
    swap(ph[hp[a]], ph[hp[b]]);
    swap(hp[a], hp[b]);
    swap(heap[a], heap[b]);
}

//向下走
void down(int a) {
    int b = a;
    if (a * 2 <= cnt && heap[a * 2] < heap[b]) b = a * 2;  //左儿子
    if (a * 2 + 1 <= cnt && heap[a * 2 + 1] < heap[b]) b = a * 2 + 1;  //右儿子
    if (a != b) {
        heap_swap(a, b);
        down(b);
    }
}

//向上走
void up(int a) {
    while (a / 2 && heap[a / 2] > heap[a]) {
        heap_swap(a / 2, a);
        a /= 2;
    }
}

//插入一个值为x的数
void insert(int x) {
    heap[++ cnt] = x;
    hp[cnt] = idx;
    ph[idx ++] = cnt;
    up(cnt);
}

//移除第k个插入的数
void remove(int k) {
    int temp = ph[k];
    heap_swap(temp, cnt --);
    up(temp);
    down(temp);
}

//将第k个插入的数更改为x
void change(int k, int x) {
    heap[ph[k]] = x;
    down(ph[k]);
    up(ph[k]);
}

int main() {
    int n, k, x;
    scanf("%d", &n);
    while (n --) {
        scanf("%s", op);
        if (strlen(op) == 1) {
            if(op[0] == 'I') {  //插入数x
                scanf("%d", &x);
                insert(x);
            }
            else if (op[0] == 'D') { //移除第k个插入的数
                scanf("%d", &k);
                remove(k);
            }
            else {
                scanf("%d%d", &k, &x);  //将第k个插入的数更改为x
                change(k, x);
            }
        }
        else {
            if (op[0] == 'P') printf("%d
", heap[1]);  //输出最小值
            else remove(hp[1]);  //移除当前最小值
        }
    }
    return 0;
}

三、集合

1、散列表 / 哈希表

数组模拟哈希表：AcWing 840. 模拟散列表

原题链接：https://www.acwing.com/problem/content/842/
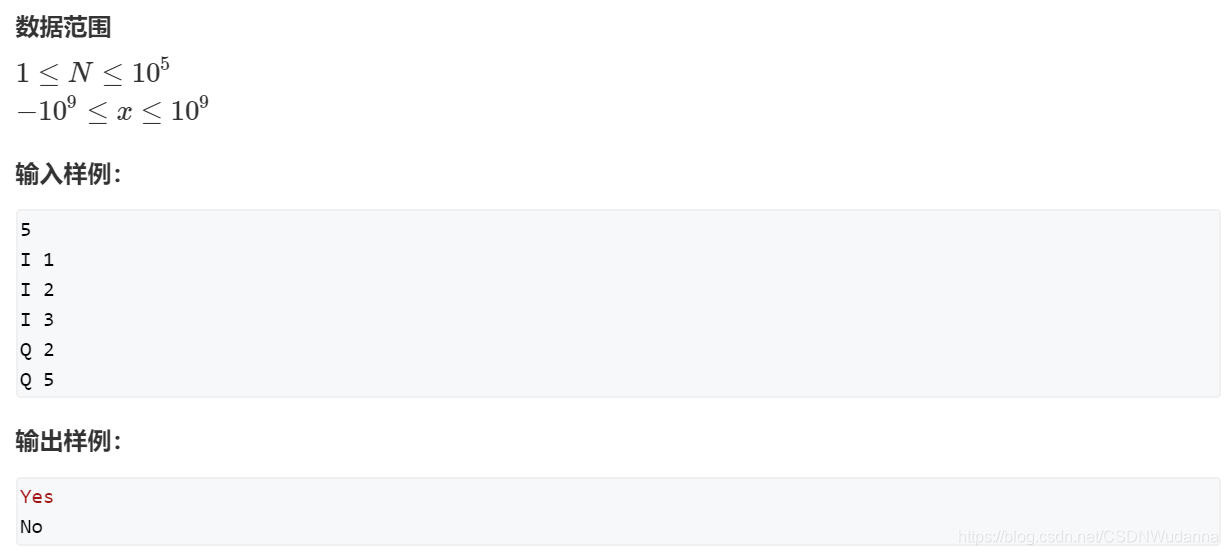
在这里插入图片描述

【注意】
一般mod是一个质数且尽可能离2的整数次幂远一点，这样能降低冲突的可能。
开放寻址法：一般要把数组开到2N~3N范围。

Ⅰ 开放寻址法

#include<iostream>
#include<cstring>

using namespace std;

const int N = 200003;  //一般哈希表要开2n到3n之间的一个质数，降低冲突的可能
const int INF = 0x3f3f3f3f;  //大于1e9

int h[N];  //哈希表
char op[9];

//如果h里面已经有x，那么返回的是x的索引
//如果h里面没有x，那么返回的是x应该插入的地方
int find(int x) {
    int a = (x % N + N) % N;  //应该先%再+，防止x很小，而N不够大去变正数
    while (h[a] != INF && h[a] != x) {
        ++ a;
        if (a == N) a = 0;  //循环
    }
    return a;
}

int main() {
    int n, x;
    scanf("%d", &n);
    memset(h, INF, sizeof(h));  //初始化
    while (n --) {
        scanf("%s%d", op, &x);
        if (op[0] == 'I') h[find(x)] = x;
        else {
            if (h[find(x)] == INF) printf("No
");
            else printf("Yes
");
        }
    }
    return 0;
}

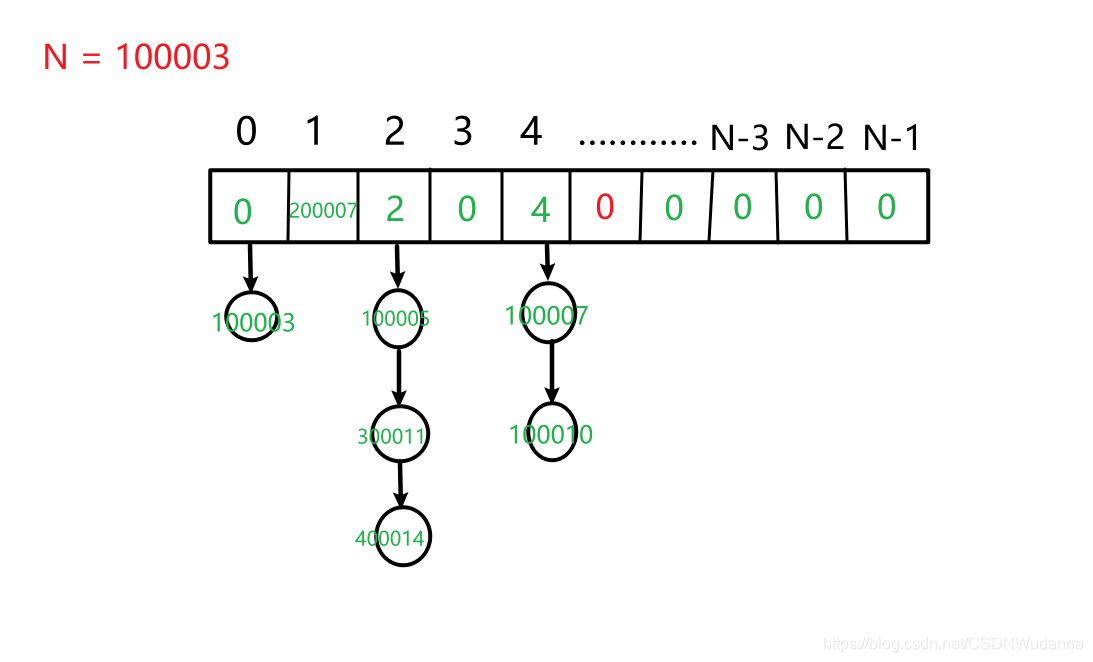
Ⅱ 拉链法

简单来说就是数组的每一个卡槽都跟一个模拟的单链表。

每一个数%N后，在数组都有对应一个位置可以放，这时候模拟单链表头插法插入元素，查询的时候就从头找起就好了。

在这里插入图片描述

#include<iostream>
#include<cstring>

using namespace std;

const int N = 100003;
const int INF = 0x3f3f3f3f;

char op[8];
// h-哈希表 e-结点 ne-next数组 idx-结点编号
int h[N], e[N], ne[N], idx = 1;

//往哈希表插入x
void insert(int x) {
	//获得x应该放在哪一个位置
    int a = (x % N + N) % N;
    //头插法
    e[idx] = x;
    ne[idx] = h[a];
    h[a] = idx ++;
}

//在哈希表查询是否存在x
bool query(int x) {
    int a = (x % N + N) % N;
    int b = h[a];
    while (e[b] != INF) {
        if (e[b] == x) return true;
        b = ne[b];
    }
    return false;
}

int main() {
    int n, x;
    scanf("%d", &n);
    memset(e, INF, sizeof e);  //初始化
    while (n --) {
        scanf("%s%d", op, &x);
        if (op[0] == 'I') insert(x);
        else {
            if (query(x)) printf("Yes
");
            else printf("No
");
        }
    }
    return 0;
}

快速判断两个字符串是否一致：AcWing 841. 字符串哈希

原题链接：https://www.acwing.com/problem/content/843/
在这里插入图片描述

思路
假如有一个字符串 str = “ABCABCDEFXYZAcWing”
那么我们现在假设有一个哈希表 h，那么：
h [ 0 ] = “” 的 hash 值
h [ 1 ] = “A” 的 hash 值
h [ 2 ] = “AB” 的 hash 值
h [ 3 ] = “ABC” 的 hash 值
h …………
在判断两个字符串是否一致时，只需要判断 h [ a ] 是否等于 h [ b ] 即可。

借一下大佬的解释：
在这里插入图片描述
注意
① 不能将 hash 值映射成0；
② 这种做法是默认了人品足够好，不存在冲突，实际上99.99%以上的概率可以保证不冲突；
③ 开 unsigned long long 不用取模，因为溢出相当于取模
④ 哈希前缀字符串除了在求字符串循环节上没有 KMP 方便，其它情况大概率上会比用 KMP 便捷很多。
⑤ P = 131 或 13331， Q = 2 ^ 64。

代码

#include<iostream>
#include<cstring>

using namespace std;

const int N = 100010;
#define ull unsigned long long

char str[N];
ull h[N], pp[N];
int p = 131;

//给h和pp数组赋值
void make_arr() {
    h[0] = 1;
    pp[0] = 1;
    int length = strlen(str);
    for (int i = 1; i <= length; ++ i) {
        h[i] = h[i - 1] * p + str[i];  //直接加
        pp[i] = pp[i - 1] * p;
    }
}

ull get(int l, int r) {
    return h[r] - h[l - 1] * pp[r - l + 1];
}

int main() {
    int n, m;
    scanf("%d%d%s", &n, &m, str + 1);
    str[0] = '1';
    int l1, r1, l2, r2;
    make_arr();
    while (m --) {
        scanf("%d%d%d%d", &l1, &r1, &l2, &r2);
        if (get(l1, r1) == get(l2, r2)) printf("Yes
");
        else printf("No
");
    }
    return 0;
}

————————————————————————
2021.03.25 整理链表 / 栈 / 队列
2021.03.28 整理字典树、并查集
2021.04.02 整理堆
2021.04.03 整理哈希表

风语者！平时喜欢研究各种技术，目前在从事后端开发工作，热爱生活、热爱工作。

上一篇
头歌计算机算法设计与分析线性规划问题和...

下一篇
【数据结构】链表OJ：力扣141.环形链表、1...

站长推荐

U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决
stm32使用HAL库配置串口中断收发数据（保姆级教程）
stm32使用HAL库配置串口中断收发数据（保姆级教程）
SpringSecurity实现前后端分离认证授权
SpringSecurity实现前后端分离认证授权
【社区图书馆】伴我前行的一本书《The C Programming Language》
【社区图书馆】伴我前行的一本书《The C Programming Language》
分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效)

您现在的位置是：首页 >技术交流 >ACM - 数据结构 - 基础（数组模拟链表 / 栈 / 队列 + 字典树 + 并查集 + 堆 + 哈希）网站首页技术交流

ACM - 数据结构 - 基础（数组模拟链表 / 栈 / 队列 + 字典树 + 并查集 + 堆 + 哈希）

数据结构

一、线性表

1、单链表

模板题：AcWing 826. 单链表

2、双链表

模板题 AcWing 827. 双链表

3、栈

数组模拟栈模板 AcWing 828. 模拟栈

逆波兰简版模板

例题1、逆波兰表达式：HDU 1237 简单计算器（写得有点复杂）

4、队列

数组模拟队列模板题 AcWing 829. 模拟队列

5、单调栈 / 单调队列

构造单峰数列

二、树型结构

1、字典树 Trie

模板题 AcWing 835. Trie字符串统计

例题1、二进制字典树：AcWing 143. 最大异或对

2、并查集

模板题 AcWing 836. 合并集合

单链表并查集 : AcWing 1242. 修改数组

根节点维护连通块结点数：AcWing 837. 连通块中点的数量

额外维护每一个结点到根节点的距离：AcWing 240. 食物链

3、堆 / 优先队列

堆排序： AcWing 838. 堆排序

维护前 m 个数：HDU 1280 前m大的数

堆的增删改查：AcWing 839. 模拟堆

三、集合

1、散列表 / 哈希表

数组模拟哈希表：AcWing 840. 模拟散列表

Ⅰ 开放寻址法

Ⅱ 拉链法

快速判断两个字符串是否一致：AcWing 841. 字符串哈希

上一篇 头歌计算机算法设计与分析线性规划问题和...

下一篇 【数据结构】链表OJ：力扣141.环形链表、1...

站长推荐

上一篇
头歌计算机算法设计与分析线性规划问题和...

下一篇
【数据结构】链表OJ：力扣141.环形链表、1...