您现在的位置是:首页 >其他 >算法记录 | Day56 动态规划网站首页其他
算法记录 | Day56 动态规划
583.两个字符串的删除操作
思路:
1.确定dp数组(dp table)以及下标的含义:dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要删除元素的最少次数
2.递推公式:
-
if (word1[i - 1]==word2[j - 1])
dp[i][j] = dp[i - 1][j - 1];
-
if (word1[i - 1]!= word2[j - 1])
- 删word1[i - 1],最少操作次数为
dp[i - 1][j] + 1 - 删word2[j - 1],最少操作次数为
dp[i][j - 1] + 1 - 同时删word1[i - 1]和word2[j - 1],操作的最少次数为
dp[i - 1][j - 1] + 2
- 删word1[i - 1],最少操作次数为
3.初始化:
从递推公式中,可以看出来,dp[i][0]和 dp[0][j]是一定要初始化的。
dp[i][0]:word2为空字符串,以i-1为结尾的字符串word1要删除多少个元素,才能和word2相同呢,很明显dp[i][0] = i。
同理:dp[0][j] = j。
4.确定遍历顺序
从递推公式dp[i][j] = dp[i - 1][j - 1] 和dp[i][j] =min(dp[i][j - 1]+1,dp[i-1][j]+1,dp[i-1][j-1]+2 中可以看出dp[i][j]都是根据左上方和正上方推出来的。从上到下,从左到右
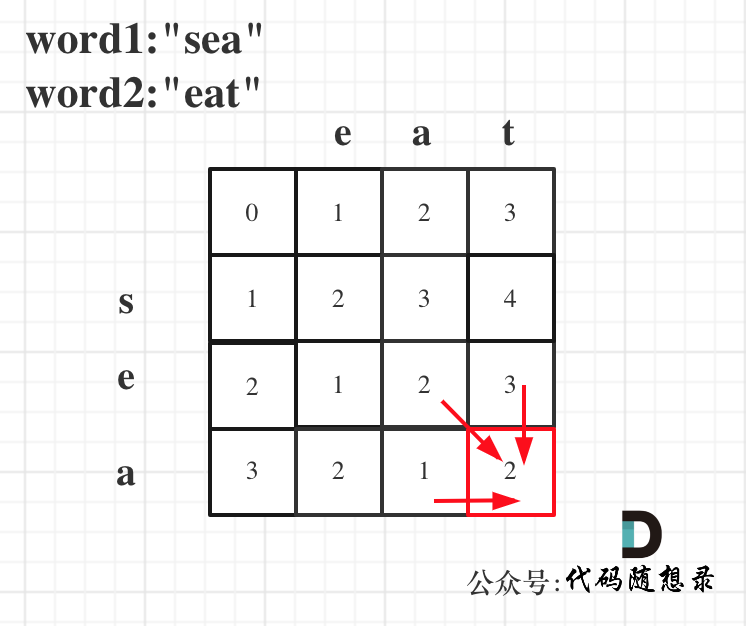
5.举例推导dp数组
以word1:“sea”,word2:"eat"为例,推导dp数组状态图如下:
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
size1 = len(word1)
size2 = len(word2)
dp = [[0] *(size2+1) for _ in range(size1+1)]
for i in range(size1+1):
dp[i][0] = i
for j in range(size2+1):
dp[0][j] = j
for i in range(1,size1+1):
for j in range(1,size2+1):
if (word1[i-1]==word2[j-1]):
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = min(dp[i-1][j]+1, dp[i][j-1]+1,dp[i-1][j-1]+2)
return dp[-1][-1]
72.编辑距离
思路:
1.确定dp数组(dp table)以及下标的含义:dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要操作的最少次数
2.递推公式:
-
if (word1[i - 1]==word2[j - 1])
dp[i][j] = dp[i - 1][j - 1];
-
if (word1[i - 1]!= word2[j - 1])
- 删word1[i - 1],最少操作次数为
dp[i - 1][j] + 1 - 删word2[j - 1],最少操作次数为
dp[i][j - 1] + 1 - 替换元素,
word1替换word1[i - 1],使其与word2[j - 1]相同,此时不用增删加元素,dp[i][j] = dp[i - 1][j - 1] + 1
word2添加一个元素,相当于word1删除一个元素,例如
word1 = "ad" ,word2 = "a",word1删除元素'd'和word2添加一个元素'd',变成word1="a", word2="ad", 最终的操作数是一样! dp数组如下图所示意的:a a d +-----+-----+ +-----+-----+-----+ | 0 | 1 | | 0 | 1 | 2 | +-----+-----+ ===> +-----+-----+-----+ a | 1 | 0 | a | 1 | 0 | 1 | +-----+-----+ +-----+-----+-----+ d | 2 | 1 | +-----+-----+ - 删word1[i - 1],最少操作次数为
3.初始化:
从递推公式中,可以看出来,dp[i][0]和 dp[0][j]是一定要初始化的。
dp[i][0]:word2为空字符串,以i-1为结尾的字符串word1要删除多少个元素,才能和word2相同呢,很明显dp[i][0] = i。
同理:dp[0][j] = j。
4.确定遍历顺序
从递推公式
dp[i][j] = dp[i - 1][j - 1]dp[i][j] = dp[i - 1][j - 1] + 1dp[i][j] = dp[i][j - 1] + 1dp[i][j] = dp[i - 1][j] + 1
从上到下,从左到右
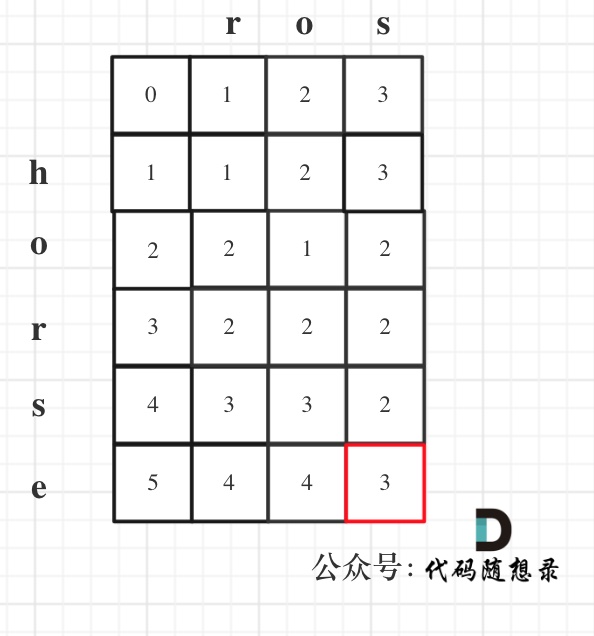
5.举例推导dp数组
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
size1 = len(word1)
size2 = len(word2)
dp=[[0]*(size2+1) for _ in range(size1+1)]
for i in range(size1+1):
dp[i][0] = i
for j in range(size2+1):
dp[0][j] = j
for i in range(1,size1+1):
for j in range(1,size2+1):
if(word1[i-1]==word2[j-1]):
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j]= min(dp[i-1][j]+1,dp[i][j-1]+1,dp[i-1][j-1]+1)
return dp[-1][-1]






 U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) Allegro16.6差分等长设置及走线总结
Allegro16.6差分等长设置及走线总结