1.问题

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2

输入：nums = [0,1,0,3,2,3]
输出：4

示例 3

输入：nums = [7,7,7,7,7,7,7]
输出：1

提示：

• 1 <= nums.length <= 2500
• -104 <= nums[i] <= 104

进阶：

你能将算法的时间复杂度降低到 O(n log(n)) 吗?

2. 解题思路

2.1 动态规划

类似674. 最长连续递增序列，我们定义：
dp_i 为以nums[i]结尾的最长递增子序列长度，则在区间[0,i)范围内，任一j，有以下判断：

• 当 nums[i]>nums[j]时，nums[i]接在nums[j]后，都能使得序列长度加1，即 dp_i= dp_j + 1;
• 否则，最长递增长度就此结束。

因此得出 状态转移方程为：

dp_i = max(dp_i , dp_j + 1), 其中 j属于区间[0, i).

由于题目已知，数组至少有一个元素，因而dp_i,j 至少为1，初始化时全都为1.

复杂度分析：

• 时间复杂度 O(N²)： 遍历计算 dp 列表需 O(N)，计算每个 dp_i 需 O(N)。
• 空间复杂度 O(N)： dp 列表占用线性大小额外空间。

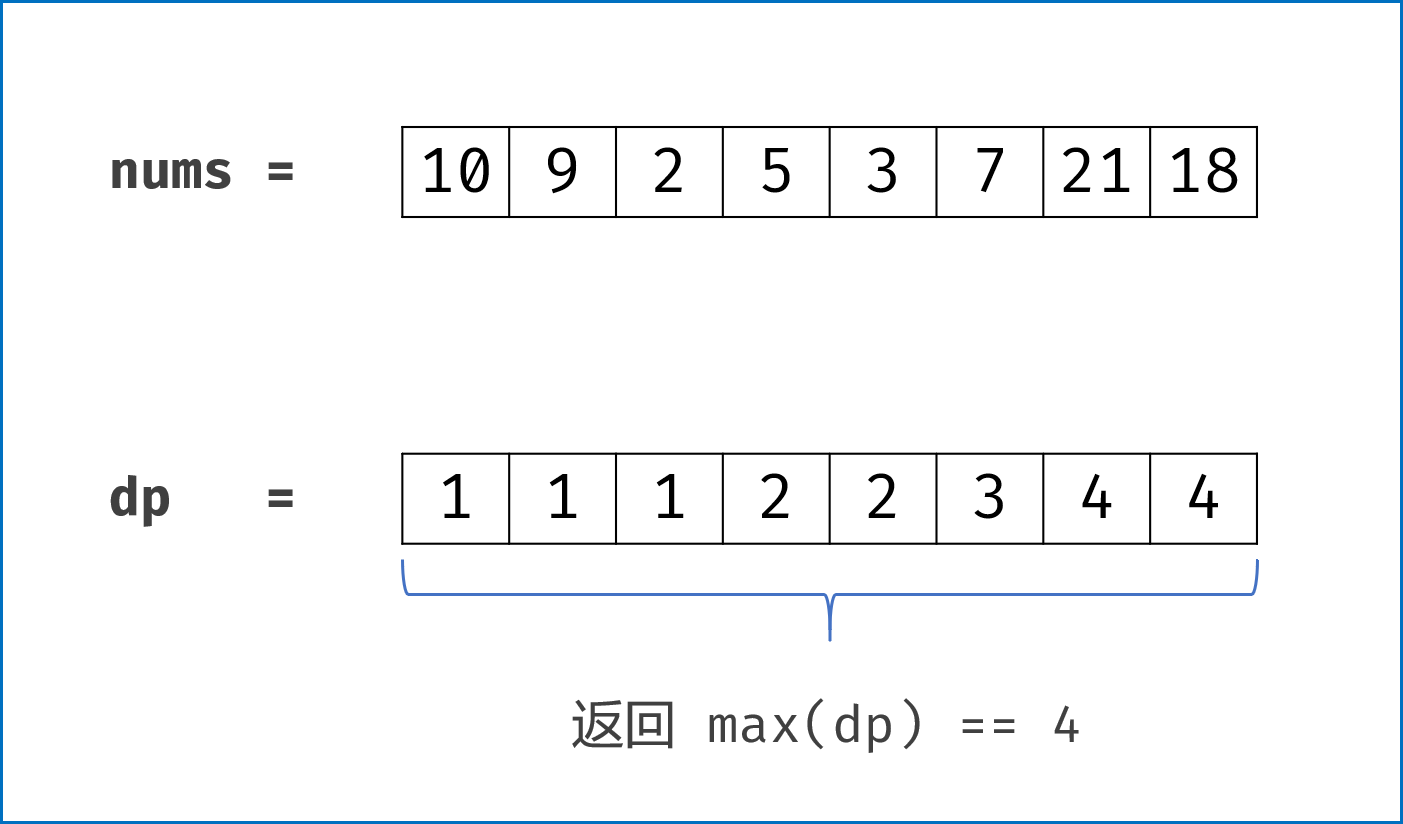
举例：nums=[10,9,2,5,3,7,21,18].

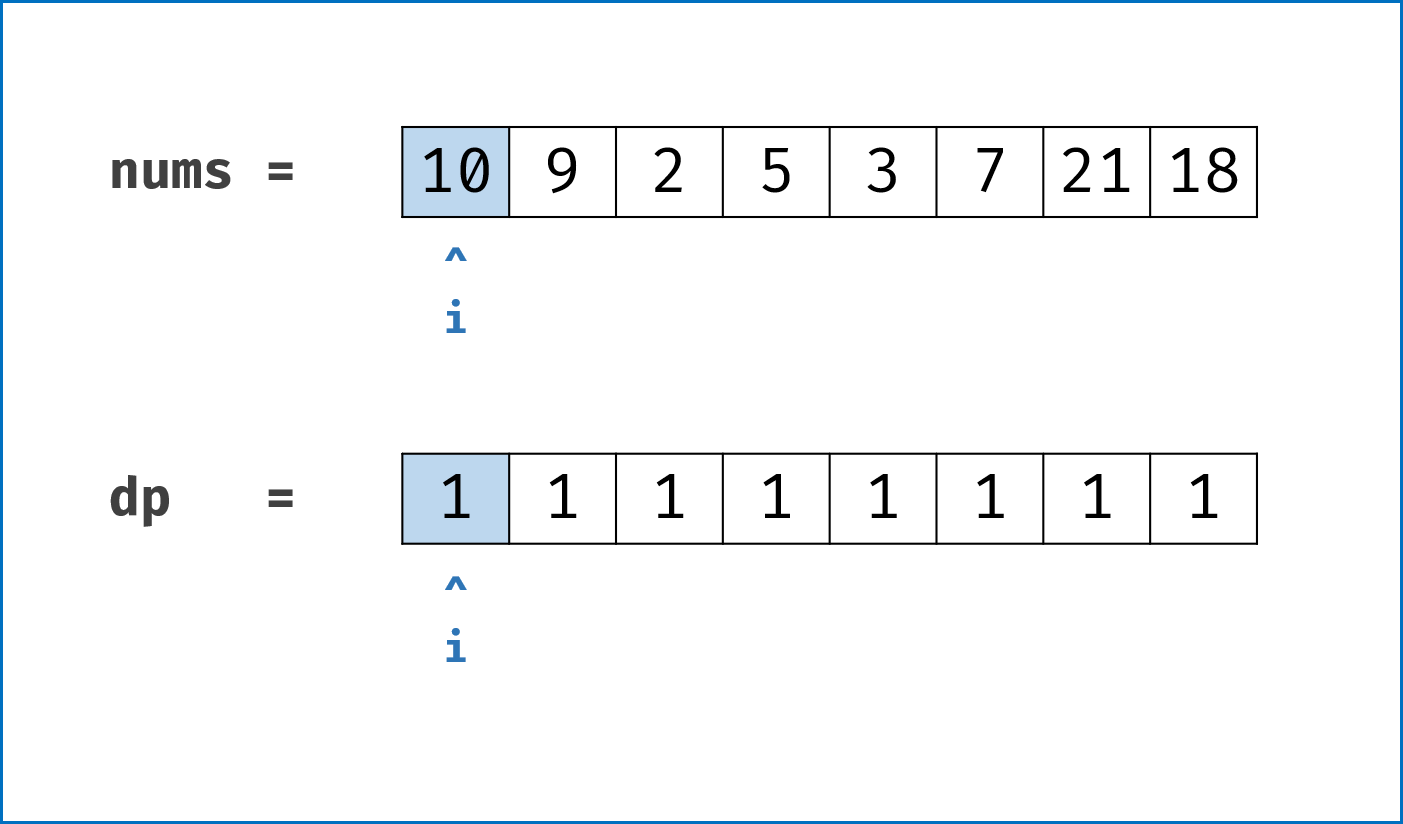
• 初始状态
  

• dp₁的值
  

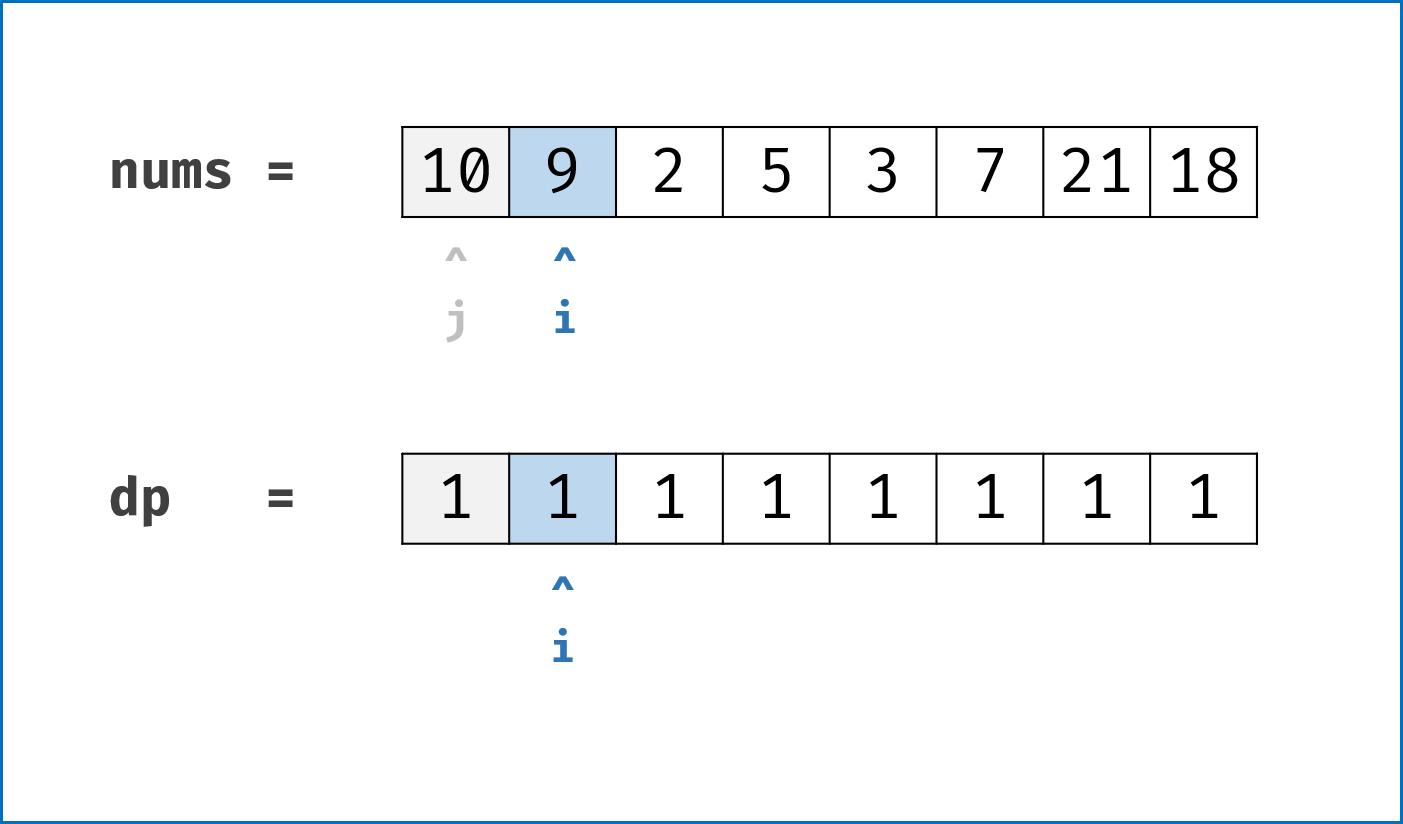
• dp₂ 的值
  

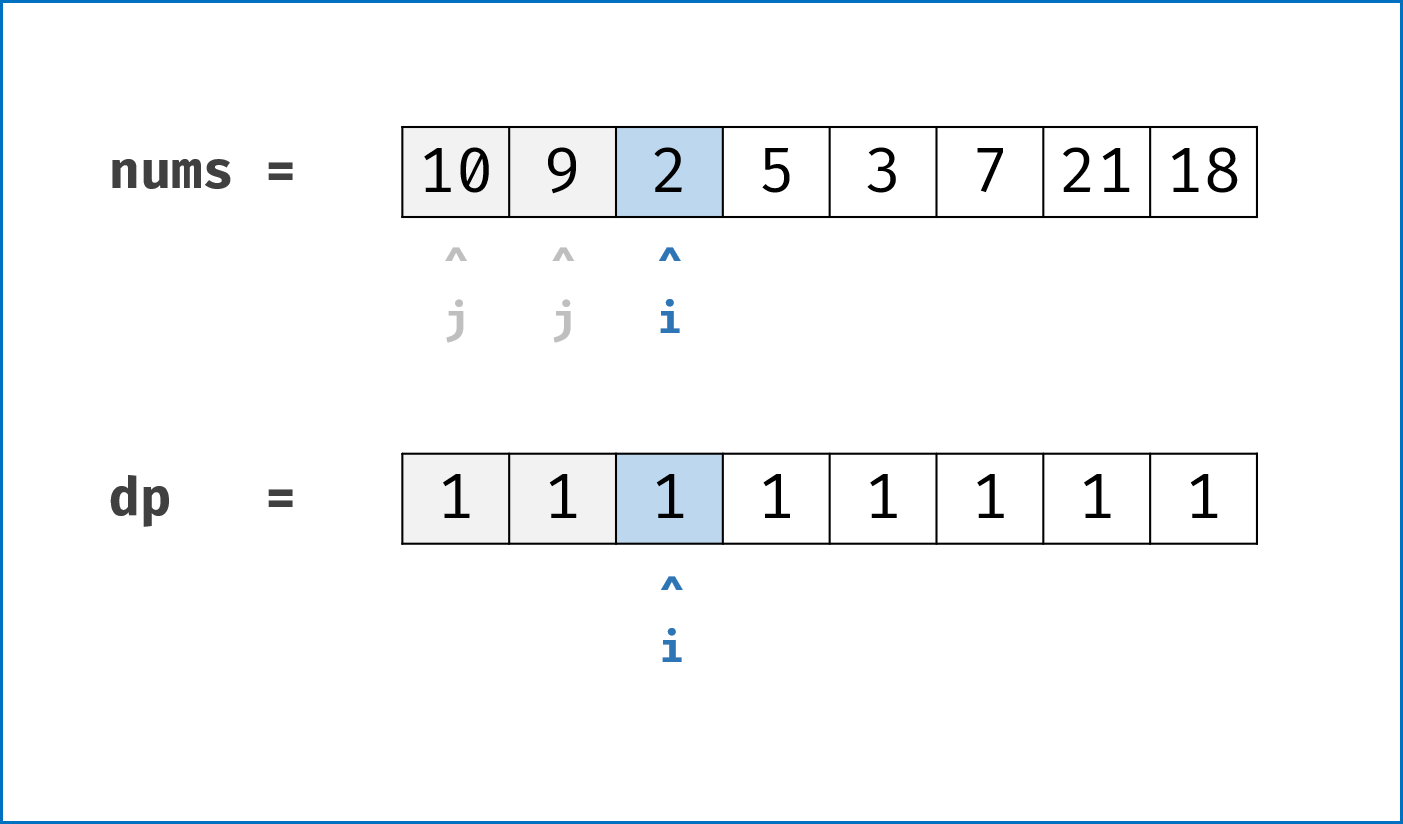
• dp₃ 的值
  

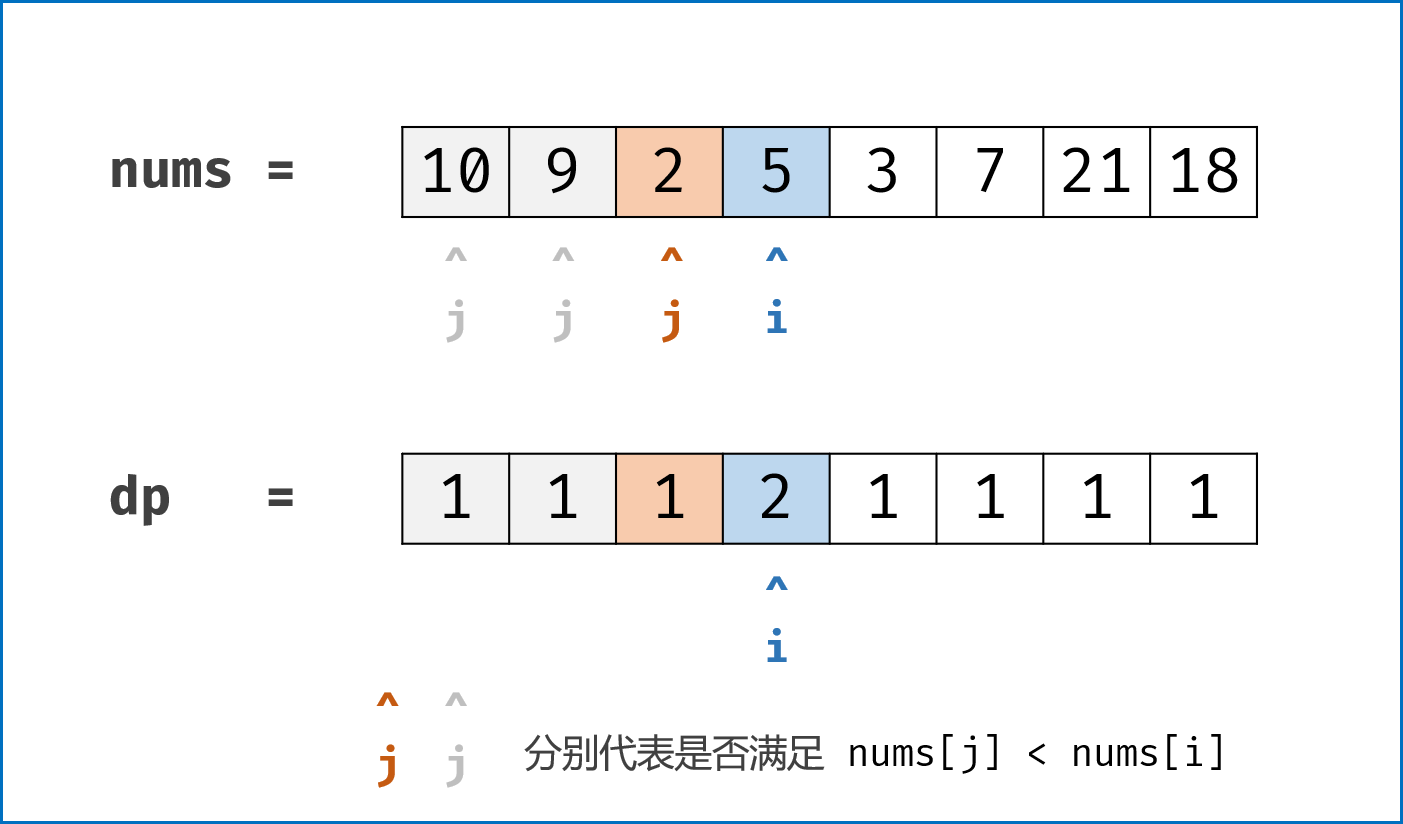
• dp₄ 的值
  

• dp₅ 的值
  

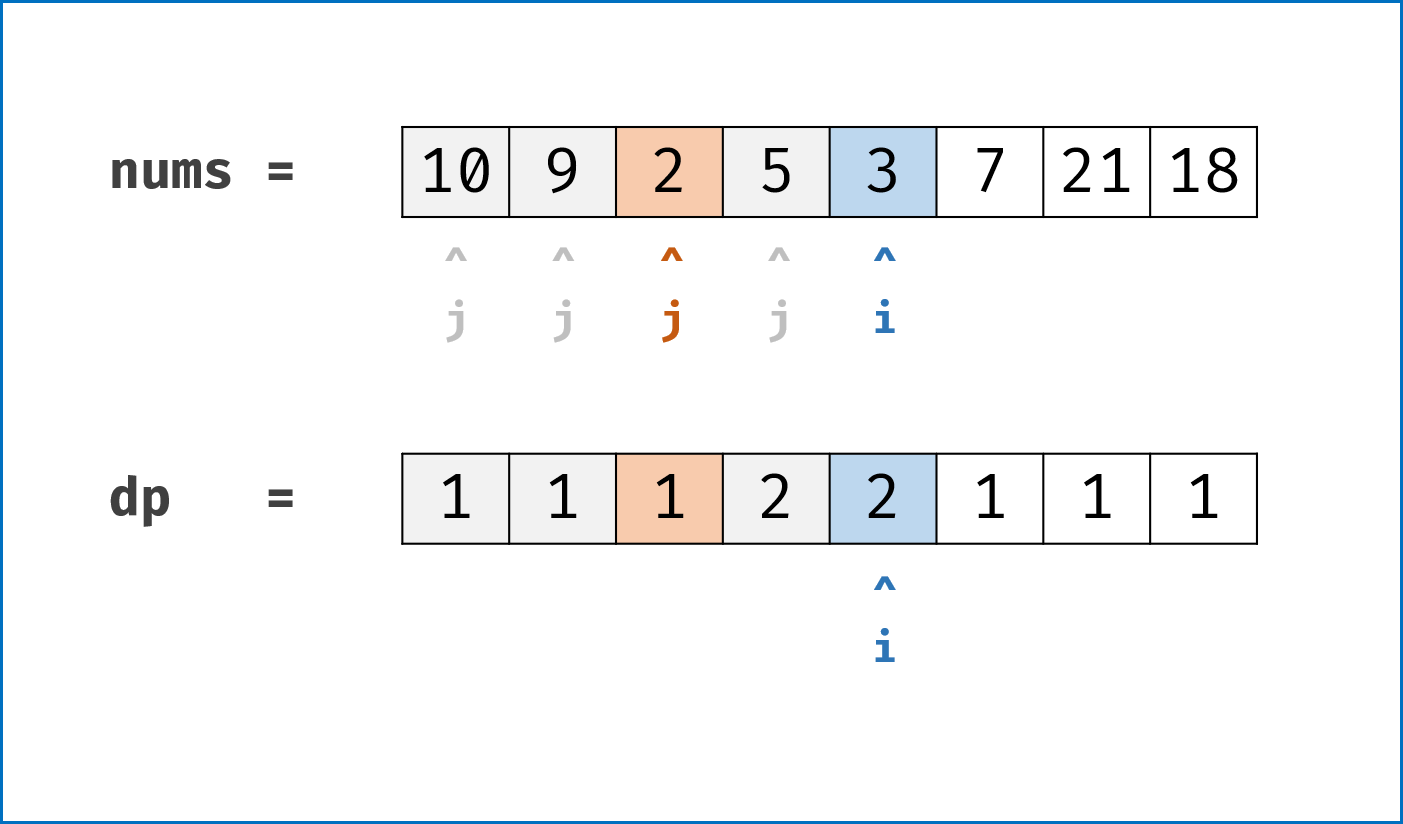
• dp₆ 的值
  

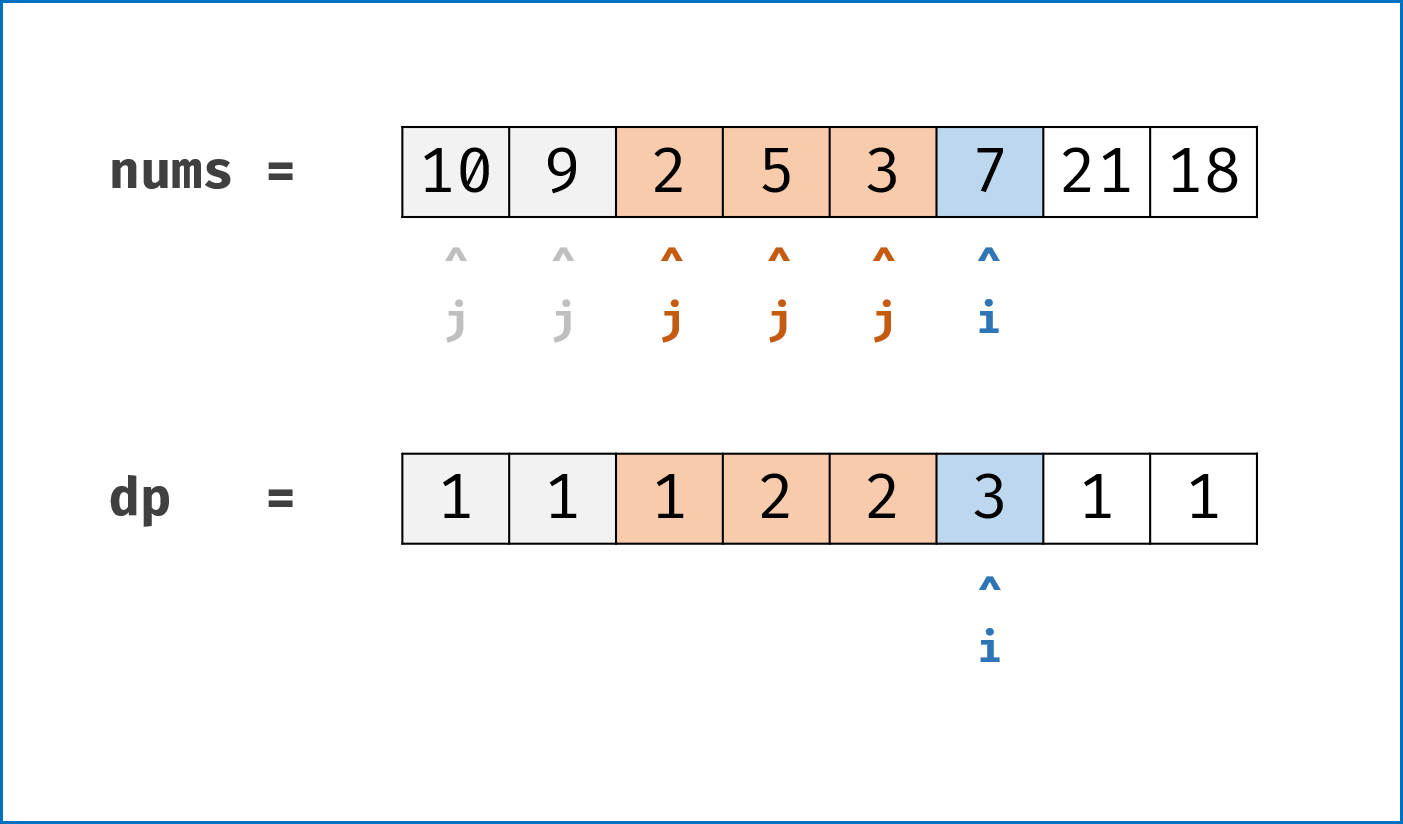
• dp₇ 的值
  

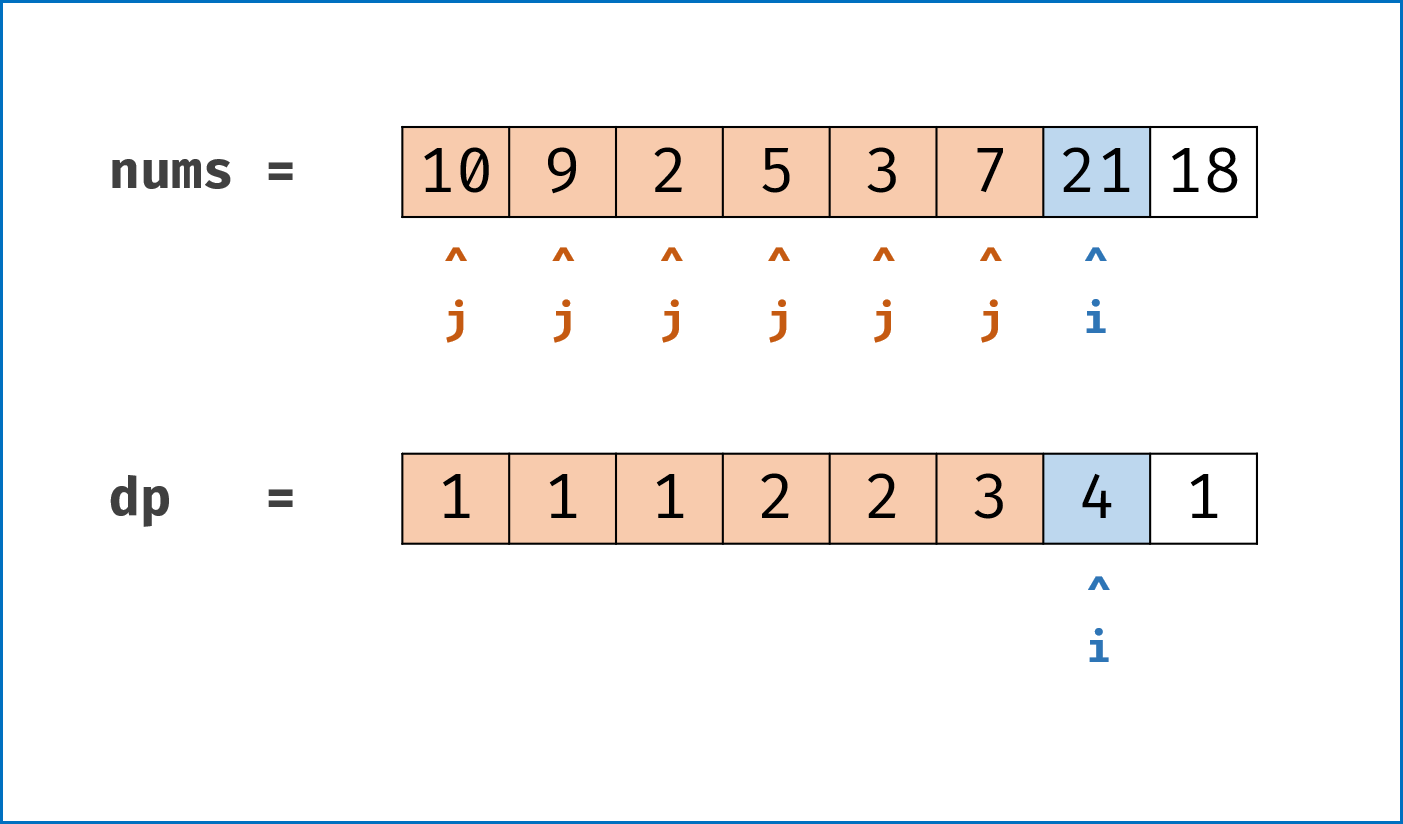
• dp₈ 的值
  

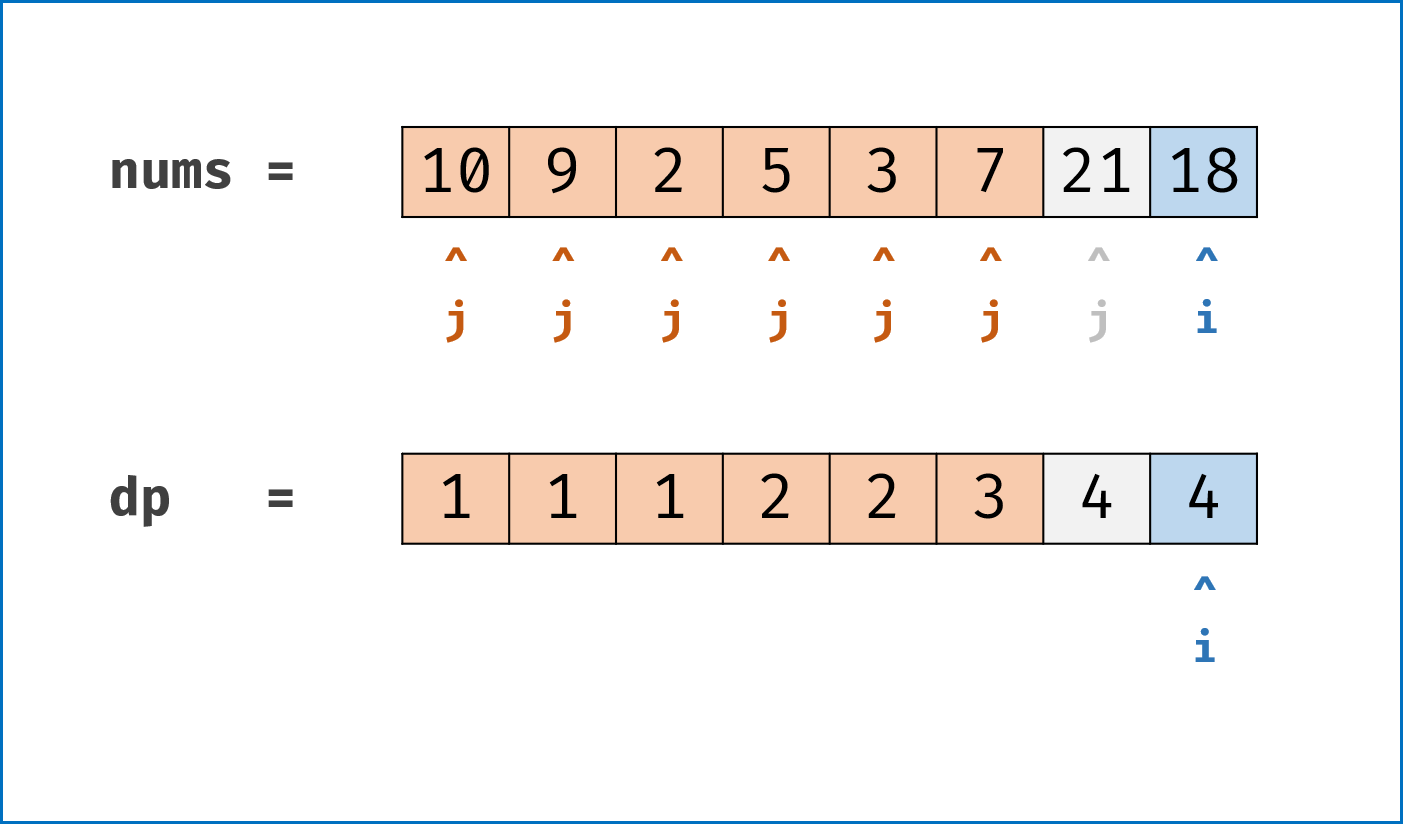
• 求max(dp)
  

2.2 动态规划+二分查找

• 状态定义：令 tails[k] 的值代表长度为 k+1 子序列的尾部元素值。

• 转移方程： 设 res 为 tails 当前长度，代表直到当前的最长上升子序列长度。设 j∈[0,res)，考虑每轮遍历 nums[k] 时，通过二分法遍历 [0,res) 列表区间，找出 nums[k] 的大小分界点，会出现两种情况：

  • 区间中存在 tails[i]>nums[k] ： 将第一个满足 tails[i]>nums[k] 执行 tails[i]=nums[k] ；因为更小的 nums[k] 后更可能接一个比它大的数字（前面分析过）。
  • 区间中不存在 tails[i]>nums[k] ： 意味着 nums[k] 可以接在前面所有长度的子序列之后，因此肯定是接到最长的后面（长度为 res ），新子序列长度为 res+1。

• 初始状态：令 tails 列表所有值为 0。

• 返回值：返回 res ，即最长上升子子序列长度。

复杂度分析：

• 时间复杂度 O(NlogN)： 遍历 nums 列表需 O(N)，在每个 nums[i] 二分法需 O(logN)。
• 空间复杂度 O(N) ： tails 列表占用线性大小额外空间。

特别注意：本方法只能用于求最长递增子序列的长度，辅助数组中的序列不是最长递增子序列：

• 例一：原序列为1，5，8，3，6，7
  辅助数组为1，5，8，此时读到3，用3替换5，得到1，3，8； 再读6，用6替换8，得到1，3，6；再读7，得到最终栈为1，3，6，7。最长递增子序列为长度4。

• 例二：原序列为1，5，8，3
  则最栈辅助数组为1，3，8。明显这不是最长递增子序列！

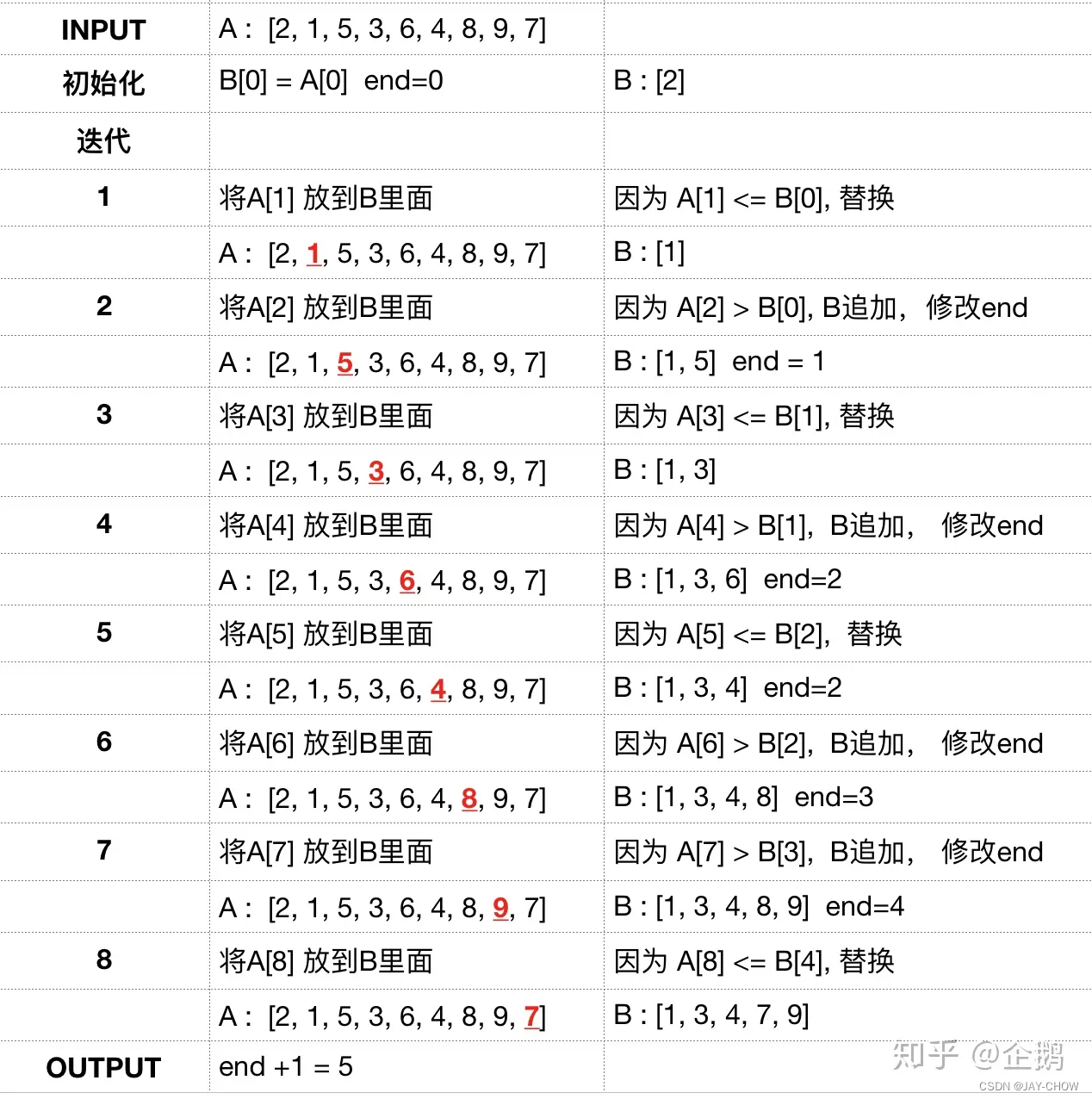
借用知乎大神 企鹅的一个例子：

3. 代码

class Solution {
    public int lengthOfLIS2(int[] nums) {
        int len=nums.length;
        int maxLen=1;
        int[] dp=new int[len+1];
        //初始化
        Arrays.fill(dp, 1);

        for(int i=1;i<len;i++){
            for(int j=0;j<i;j++){
            	//符合拼接在原有序列之后的条件，则dp[j]+1,max是为了保证dp[i]永远是最大值； 否则 置为1
                if(nums[i]>nums[j]){
                    dp[i]=Math.max(dp[j]+1,dp[i]);
                }
            }
            //计算当前范围[0,i]的最大值
            maxLen=Math.max(maxLen, dp[i]);
        }
        return maxLen;
    }

	//动态规划+二分查找
    public int lengthOfLIS(int[] nums) {
        int[] tails = new int[nums.length];
        int res = 0;
        for(int num : nums) {
            int i = 0, j = res;
            while(i < j) {
                int m = (i + j) / 2;
                if(tails[m] < num) i = m + 1;
                else j = m;
            }
            tails[i] = num;
            if(res == j) res++;
        }
        return res;
    }

// 作者：Krahets
// 链接：https://leetcode.cn/problems/longest-increasing-subsequence/solutions/24173/zui-chang-shang-sheng-zi-xu-lie-dong-tai-gui-hua-2/
// 来源：力扣（LeetCode）
// 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
}