您现在的位置是:首页 >技术杂谈 >剑指 Offer 34. 二叉树中和为某一值的路径 / LeetCode 113. 路径总和 II(深度优先搜索)网站首页技术杂谈
剑指 Offer 34. 二叉树中和为某一值的路径 / LeetCode 113. 路径总和 II(深度优先搜索)
简介剑指 Offer 34. 二叉树中和为某一值的路径 / LeetCode 113. 路径总和 II(深度优先搜索)
题目:
链接:剑指 Offer 34. 二叉树中和为某一值的路径;LeetCode 113. 路径总和 II
难度:中等
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
示例 1:
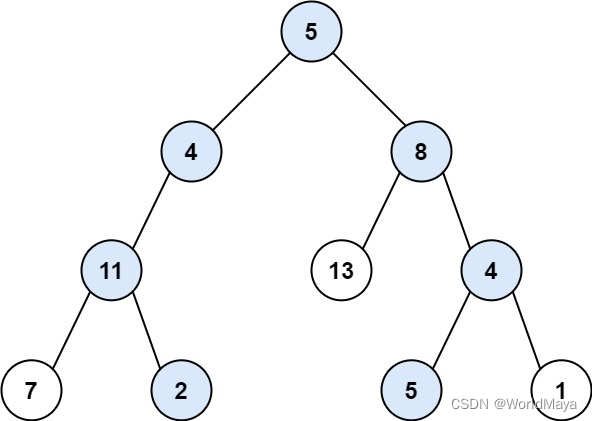
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:[[5,4,11,2],[5,8,4,5]]
示例 2:
输入:root = [1,2,3], targetSum = 5
输出:[]
示例 3:
输入:root = [1,2], targetSum = 0
输出:[]
提示:
- 树中节点总数在范围 [0, 5000] 内
- -1000 <= Node.val <= 1000
- -1000 <= targetSum <= 1000
深度优先搜索(二叉树先序遍历):
简单的深搜。用一个遍历数组path记录遍历路径,仅在遍历到叶子节点时将path路径中的节点计算总和并判断是不是等于目标和,遍历到非叶子节点时继续向左右子树搜索。一个分支遍历完,回溯时将当前节点从遍历路径中删除。
详细请看代码注释。
代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> ans; // 所有目标路径
vector<int> path; // 记录深搜遍历的路径
int targetSum; // 给定目标
void dfs(TreeNode* root, vector<int> &path) {
path.emplace_back(root->val); // 遍历到的节点加入遍历路径中
if(root->left == nullptr && root->right == nullptr) { // 叶子结点,计算路径总和
int sum = 0;
for(auto a : path) sum += a;
if(sum == targetSum) ans.emplace_back(path); // 路径总和等于给定目标和
}
else { // 非叶子节点
if(root->left != nullptr) dfs(root->left, path); // 向左子树搜索并传递当前遍历路径
if(root->right != nullptr) dfs(root->right, path); // 向右子树搜索并传递当前遍历路径
}
path.pop_back(); // 当前分支遍历完,回溯时将当前节点从遍历路径中删除
}
vector<vector<int>> pathSum(TreeNode* root, int target) {
if(root == nullptr) return ans; // 空树没有目标路径
targetSum = target;
dfs(root, path);
return ans;
}
};
时间复杂度:O(N2)。
空间复杂度:O(N)。
风语者!平时喜欢研究各种技术,目前在从事后端开发工作,热爱生活、热爱工作。






 QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) Allegro16.6差分等长设置及走线总结
Allegro16.6差分等长设置及走线总结