前言：ICCV2019点云特征提取点卷积InterpoConv

Interpolated Convolutional Networks for 3D Point Cloud Understanding

引言

点云是不规则、无序、且稀疏的
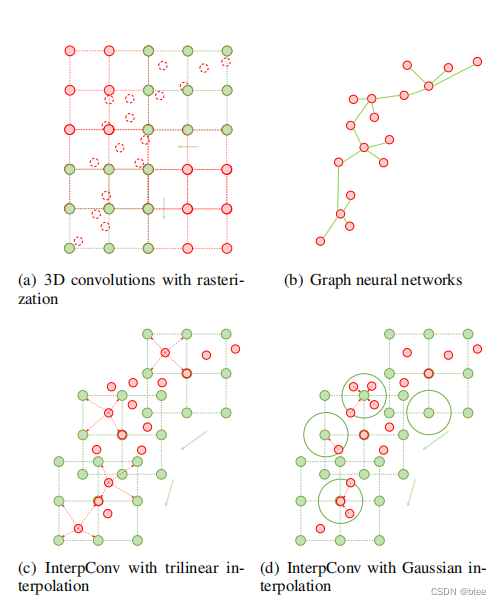
处理这样的点云数据有两大类方法
第一：voxel化

directly rasterize irregular point clouds into regular voxel grids, and adopts standard 3D convolutions to learn shape features.

缺点：会丢失掉一些几何信息，并且造成计算负担

the transformation of irregular inputs leads to a loss of geometric information, and convolutions on dense voxel grids lead to heavy computational burden.

第二：在欧几里得空间或特征空间建立一个局部图，然后用连续的核作用在每个图的边缘上，来学习到几何特征，这个连续的核的就用MLP来学习
缺点：图的构造不是稀疏不变的，点的密度不同导致图的构造不同
其次，用MLP学习连续核的效果不太好

这篇文章中，提出了一种l Interpolated Convolution operation (InterpConv)方法，用了离散的卷积核和插值方法来学习几何关系和权重坐标。

方法

离散卷积核

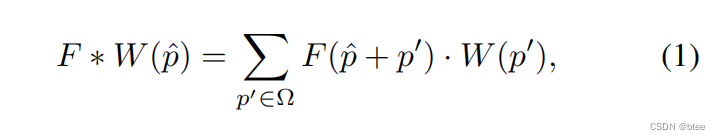
对不同位置的P‘,有一个对应的权重W(p’)，与原有的不同邻点的特征相乘再相加

连续卷积核

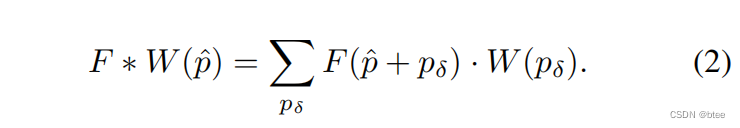
对于一个（pdelat）相对位置，直接用MLP将相对位置映射到高维特征作为这个位置的权重
预测连续的卷积核的缺点在于，并不一定能其效果，预测的参数太多了并且很不高效

因此，我们的方法选择离散核的方式

构建离散核的同时保留距离信息，我们将这个构建的方式拆成两个步骤
空间离散核权重：
是一组长为C的向量
插值函数：核权重向量的坐标和输入邻点坐标
归一化参数Np
InterpConv公式如下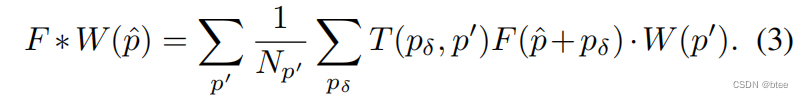
离散核
离散核维一组在3D欧几里得空间的向量，每个向量有一个3D坐标来存储C维向量，这个向量可以被初始化也可以被更新
坐标可以固定也可以被更新
我们在这里用立方体来存储核

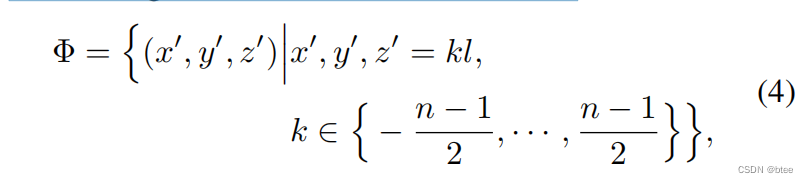
相对坐标作为核的3D位置坐标信息，同时对除以距离L。L表示两个相邻权重向量之间的距离。
距离L的作用，控制感受野，获得更精细的结构信息，当点很密集的时候

It determines the actual 3D size of a kernel in the Euclidean space and is defined to control the receptive field, from which one convolutional kernel can “see” input point clouds. If l is small, the convolutional kernel is able to capture fine-grained local structures, otherwise it encodes more global shape information.

插值函数
插值函数文中介绍了两种，一种是三线性插值，一种是高斯插值


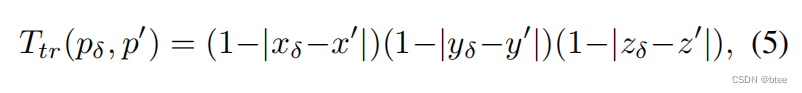
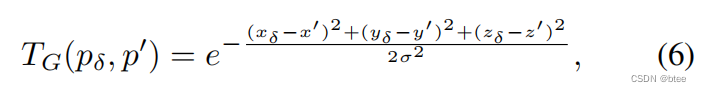
归一化项
由于邻点数不固定，因此需要归一化
归一化的第一种方式，加权求和除以邻点数

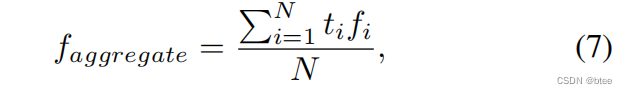
第二种，加权求和除以权重的总和

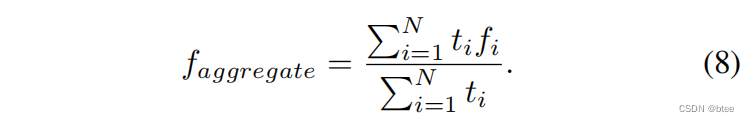
伪代码

在所有输入点中采样p个点，对p个点中的每个点
对每个核的核点位置：
对每个邻点：
pdelta记录邻点的相对位置关系，将位置关系在位置核函数中进行插值，得到位置权重向量t
用得到的位置权重向量乘原始特征再相加，得到最终的每个点的聚合特征
得到不同核作用后的特征
用聚合后的特征与卷积核作用，得到卷积后的特征向量

网络

分类网络（采用类似Inception网络模块方法）

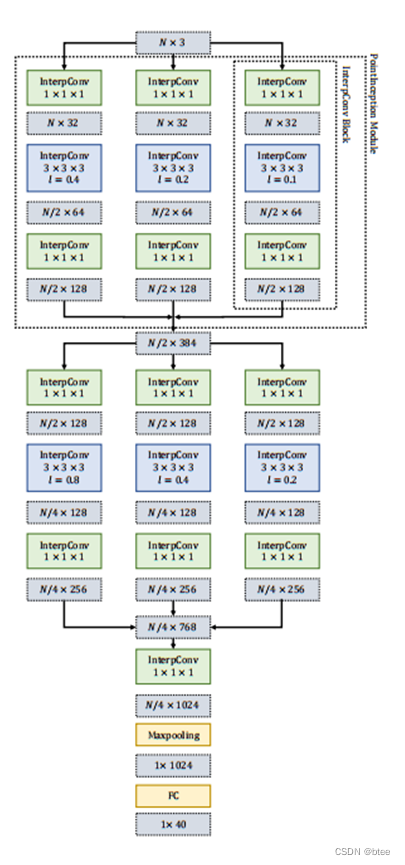
分割网络

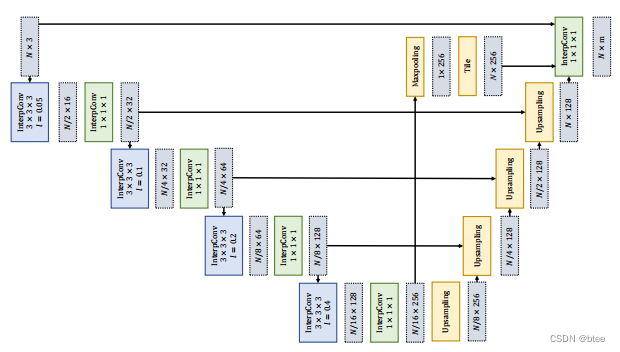
实验

分类效果

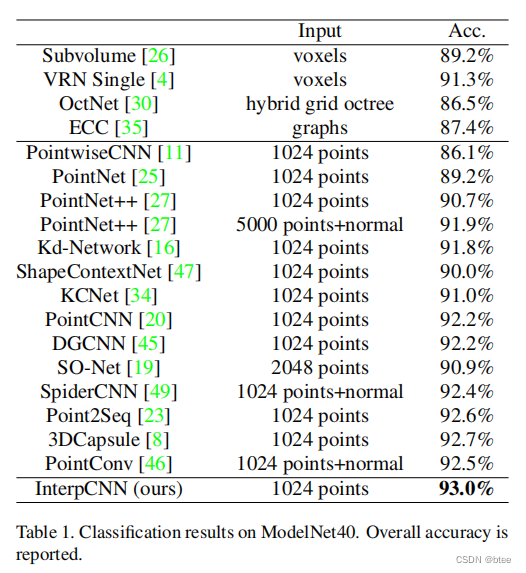
分割效果

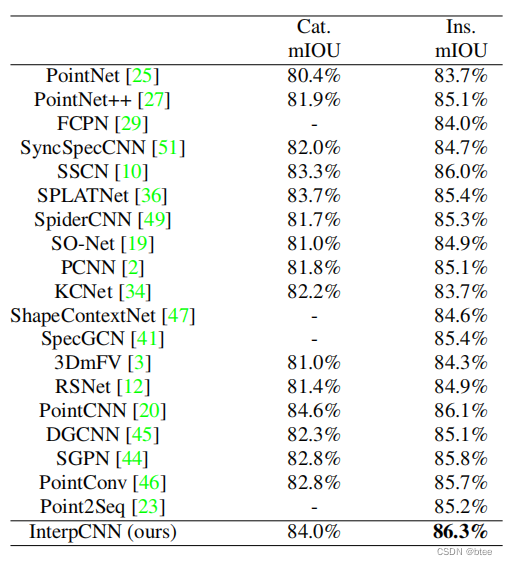
总结

插值函数在点云邻域里用得比较多，有的是直接对规则卷积核插值，这篇文章是对特征插值再应用离散卷积