前言

嵌入式软件开发过程中或多或少都会遇到一些最优值寻找的过程，比如控制过程中寻找最小电流、电压、温度以及某些最优系数等。解决寻找最优值的过程就寻优算法，传统寻优算法依靠线性单调手段轮训查找，对多极值处理不佳，难以从多极值中找到最值，陷入局部最优。智能的寻优算法大多具备仿生原理实现迭代进化，计算量较大，普通单片机算力有限对于一些计算量大的通用算法实现起来较为费时费力，粒子群实现起来较为简单，计算量小于其它优化算法，同时有具备一定的智能算法的优势，因此本文挑选了粒子群算法来实现通用的单片机智能寻优算法。

一、寻优、粒子群优化简介

寻优又叫优化，本意就是寻找最值，从一堆数据中找到最满足限制条件的数值。当限制条件不止一个时还要考虑使用不同的系数权重进行限制条件的叠加。如果寻找的数值不止一个而是一组，便是多元优化问题，产生的最优解很有可能是最优解集(多组均满足条件的集合)。
粒子群优化缩写为PSO(Particle Swarm Optimization)，是常用的优化算法一种，通过仿生模拟鸟群在地面捕食的动态情况从而实现寻找食物最多的位置。每个鸟被拟化为一个粒子，没有质量和体积只具备位置和速度信息，随着不断地更新迭代，粒子向最近的最优位置运动，迭代完毕后哪个位置粒子数最多哪个位置便被视为最优解。其它常见的优化算法也具备相同原理如：遗传优化算法、蚁群优化算法、BP神经网络优化算法等，但粒子群优化算法实现简单，计算量小，易于实现等更适合在单片机上进行尝试应用。

二、粒子群寻优基本原理

2.1 模型概述

鸟群捕食过程就是一种自然界寻优的过程，一群鸟在一块区域中捕食，初始时刻是随机分布的，每只鸟可感知自己附近食物的多少，当前时刻总有一只鸟发现自己附近的食物很多，下一时刻食物少的鸟会主动靠近食物多的鸟，因此随着不断地向食物多的鸟的附近聚集最终即可发现当前区域中食物最多的位置。

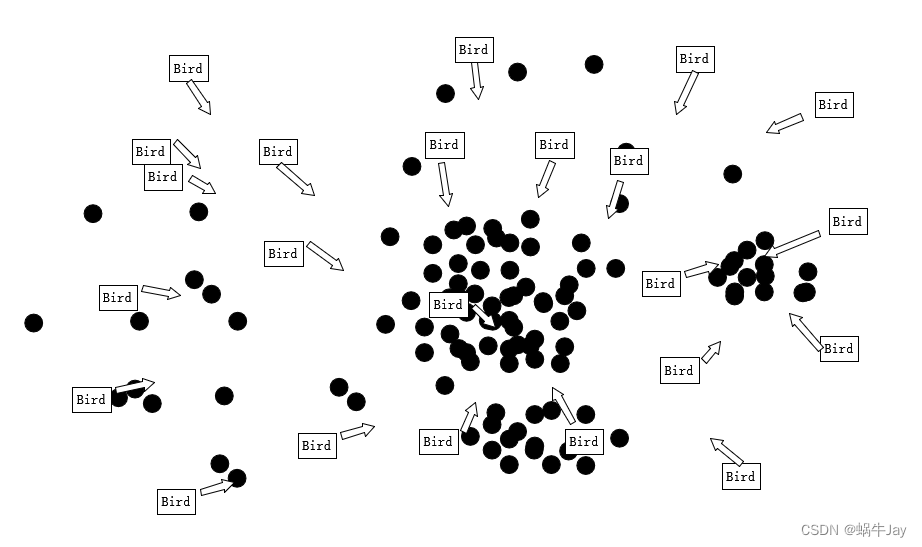
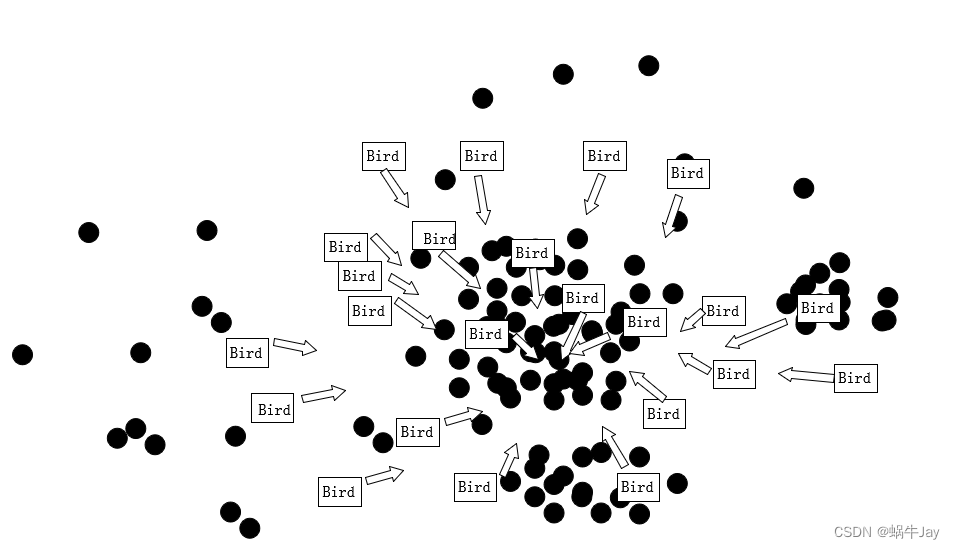
2.2 理论公式

将鸟抽象为一个粒子，鸟的数量为粒子的数量n，鸟在空间中的位置可由m维的位置向量X=(x1,x2,x3,…,xm) 表示，在空间中的速度向量V=(v1,v2,v3,…,vm),鸟附近的食物的多少可认为是鸟在环境中生存下去的程度，叫做适应度，一只鸟从初始进入空间位置更新到当前时刻位置中适应度最大时的位置Pi=(pi1,pi2,pi3,…,pim)称为个体极值,在鸟这个群体中，适应度最大值也就是极值中的极值称为群体极值Pg=(pg1,pg2,pg3,…,pgm).
则更新公式为

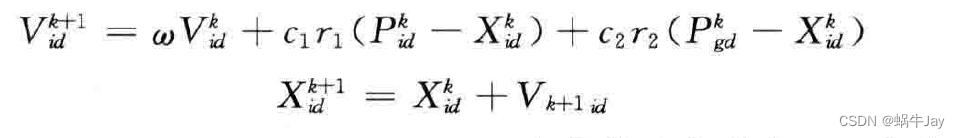
上式中 w为惯性权重，越大代表位置趋向于保持原来位置，d=1,2,…,m i=1,2,…,n ；k为当前迭代的次数；c1 c2为加速度因子，r1 r2是分布于0-1间的随机数。
由上式可看出粒子位置的更新依赖三部分：原有位置，个体极值位置以及群体极值位置。随机数的增加模拟了自然界的随机性。一般经过固定的迭代次数后，群体极值就是我们想要的目标结果。

三、C++代码实现

3.1 算法流程图

3.2 源码

基于STM32F407实现C++的封装

头文件如下

#ifndef __PUB_PSO
#define __PUB_PSO
#include "stdint.h"
#include "stm32f4xx_rng.h"
const uint32_t NUM=10;//粒子总数
const uint32_t DIM=1;//维度，即变量数目

typedef struct 
{
	float x[DIM];//当前位置
	float f;//当前适应度 性能评估指标
	float v[DIM];//当前速度	

 	float bestx[DIM];//当前粒子历史最优位置   
	float bestf;//当前粒子历史最优适应度 性能评估指标
	
}PSO_SWARM;
typedef struct 
{
	float w;//惯性项系数
	float c1;//个体寻优项系数
	float c2;//集体寻优项系数

	float max_gen;//最大进化次数
	float (* FUNC_fit) (float*);//适应度函数指针
	float xmin[DIM];//位置下限
	float xmax[DIM];//位置上限
	
	float gbestx[DIM];//全局最优位置
	float gbestf;//全局最优适应度 性能评估指标
}PSO_INITSET;

class pub_pso
{

/*---------DATA-----------*/		
public:
	float w;//惯性项系数
	float c1;//个体寻优项系数
	float c2;//集体寻优项系数

	float max_gen;//最大进化次数

	float (* FUNC_fit) (float*);//适应度函数指针

	float xmin[DIM];//位置下限
	float xmax[DIM];//位置上限
	float gbestx[DIM];//全局最优位置
	float gbestf;//全局最优适应度 性能评估指标
	PSO_SWARM pso_swarm[NUM];//粒子
private:
	
/*------------FUNCTION----------*/	
public:
	pub_pso(){};
	~pub_pso(){};	
void InitValue(void);
void PSOInstall(PSO_INITSET*pso_initset);
void Evolution(void);
void Seekgbest(void);
void Run(void);
private:

		
};
extern pub_pso pso;
extern "C" void RNG_Init(void);
extern "C" float rand(void);
#endif

源文件如下

#include"pub_PSO.h"
#include"stm32f4xx_rcc.h"
void RNG_Init(void)
{
  RCC_AHB2PeriphClockCmd(RCC_AHB2Periph_RNG, ENABLE);
	RNG_Cmd( ENABLE);

}
pub_pso pso;
float rand(void)
{
	int temp;
	while(!RNG_GetITStatus( RNG_FLAG_DRDY));
	temp=RNG_GetRandomNumber()%(1000-0+1)+0;
return temp;
}

float finit(float *x)
{

return 1;
}

void pub_pso::InitValue(void)
{

    for(int each=0;each<NUM;each++)//更新每一个粒子
    {
        PSO_SWARM *p=&pso_swarm[each];
        for (int i = 0; i < DIM; i++)//初始粒子均匀分布
        {
					p->v[i]=0;
          p->x[i]= each*(xmax[i]-xmin[i])/NUM+xmin[i];
        }
        p->f = FUNC_fit(p->x);//计算适应度值

					for (int j = 0; j < DIM; j++)//局部最优初始化
					{
						p->bestx[j]= p->x[j];
					}
					p->bestf=p->f;

    }
		for (int j = 0; j < DIM; j++)//全局最优初始化
					{
						gbestx[j]= pso_swarm[0].x[j];
					}
					gbestf=pso_swarm[0].f;	
//	gbestf=pso_initset->gbestf;//全局最优适应度 性能评估指标

}

void pub_pso::PSOInstall(PSO_INITSET*pso_initset)
{
//	w=pso_initset->w;//惯性项系数
	c1=pso_initset->c1;//个体寻优项系数
	c2=pso_initset->c2;//集体寻优项系数

	max_gen=pso_initset->max_gen;//最大进化次数
	for (int i = 0; i < DIM; i++)//更新每一个粒子的每一个维度，
	{
		xmin[i]=pso_initset->xmin[i];//位置下限
		xmax[i]=pso_initset->xmax[i];//位置上限
//		gbestx[i]=pso_initset->gbestx[i];//全局最优位置
	}
}
void pub_pso::Evolution(void)
{
    for(int each=0;each<NUM;each++)//更新每一个粒子
    {
        PSO_SWARM *p=&pso_swarm[each];
        for (int i = 0; i < DIM; i++)//更新每一个粒子的每一个维度，
        {
					p->v[i]=p->v[i]*w + c1 * rand() * (p->bestx[i]-p->x[i])
								+ c2 * rand() * (gbestx[i]-p->x[i]);
          p->x[i] += p->v[i];
					if(p->x[i]<xmin[i])p->x[i]=xmin[i];
					if(p->x[i]>xmax[i])p->x[i]=xmax[i];
        }
        p->f = FUNC_fit(p->x);//计算适应度值
				if(p->bestf > p->f)//更新个体最优
				{
					for (int j = 0; j < DIM; j++)
					{
						p->bestx[j]= p->x[j];
					}
					p->bestf=p->f;
				}
				if(gbestf > (p->f))//更新全局最优 异步更新，后续粒子会使用新的全局最优 速度快容易陷入局部最优
				{
					for (int j = 0; j < DIM; j++)
					{
						gbestx[j]= p->x[j];
					}
					gbestf=p->f;
				}
    }

}

void pub_pso::Run(void)
{
    InitValue();//种群初始化
    for(int gen=0;gen<max_gen;gen++)//循环演变
    {
				w= 0.9f-gen*0.5f/max_gen;//线性变化惯性速度权重
        Evolution();//粒子进化一次//寻找全局最优
    }
}

上述函数需要自行添加float finit(float *x)函数的具体内容，后续可做成函数指针形式引入。随机数的使用调用了STM32F4的随机数寄存器进行获取。
使用主要为初始化后再开启优化后调用void pub_pso::Run(void)函数，结束后提起群体极值即可。

四、应用示例

1.最值寻找

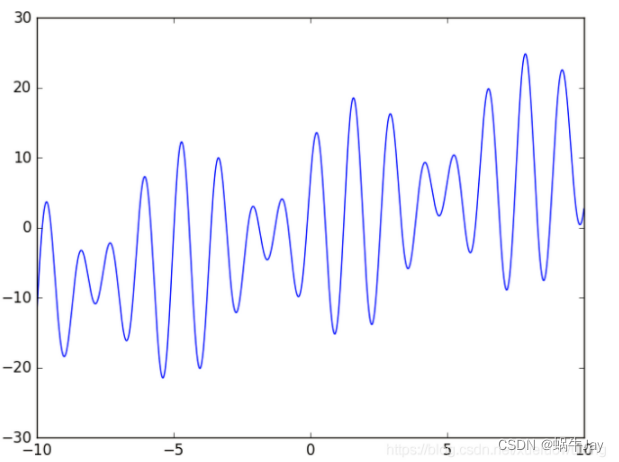
求上述函数的最大值

1.PID参数寻优

PID调参是一个比较麻烦的过程，这个过程可以利用粒子群优化算法取寻找一个。PID的系数可当做粒子群的位置参数进行输入，适应度函数通常采用误差性能指标ITAE进行定义，

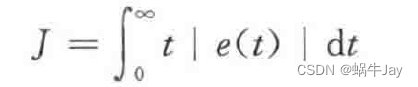
离散化后在单片机中可定义为输入PID参数后，固定时长内时间无误差的累计之和。如系统反应时间为5s，ITAE=1误差(1s时刻时)+2误差(2s时刻时)+3误差(3s时刻时)+4误差(4s时刻时)+5*误差(5s时刻时)。

总结

从基本原理进行了介绍寻优及粒子群优化算法，贴出了C++源码及应用示例的简述。

参考资料

1.MATLAB智能算法30个案例分析
2.超简洁的随机粒子群算法（PSO）程序（C/C++）