灰色系统理论是一种研究少数据、贫信息、不确定性问题的新方法，它以部分信息已知，部分信息未知的“小样本”，“贫信息”不确定系统为研究对象，通过对“部分”已知信息的生成、开发，提取有价值的信息，实现对系统运行行为、演化规律的正确描述和有效监控。

灰色理论强调通过对无规律的系统已知信息的研究，提炼和挖掘有价值的信息，进而用已知信息取揭示未知信息，使系统不断“白化”。

灰色系统中建立的模型称为灰色模型（Grey Model），简称GM模型，该模型是以原始数据序列为基础建立的微分方程。

灰色建模中最有代表性的模型是针对时间序列的GM建模，它直接将时间序列数据转化为微分方程，利用系统信息，使抽象的模型量化，进而在缺乏系统特性知识的情况下预测系统输出。

灰色神经网络预测流程包含灰色神经网络构建，灰色神经网络训练和灰色神经网络预测三个部分。

其中，灰色神经网络构建根据输入输出数据维数确定灰色神经网络结构。

由于本案例输入数据为5维，输出有1维，所以灰色神经网络结构为1-1-6-1，即LA层有1个节点，输入为时间序列t,LB层有1个节点，LC层有6个节点，从第2个到第6个分别输入市场份额、需求趋势、价格波动、订单满足率、分销商联合预测等5个因素的归一化数据，输出为预测订单量。

灰色神经网络训练用训练数据训练灰色神经网络，使网络具有订单预测能力。

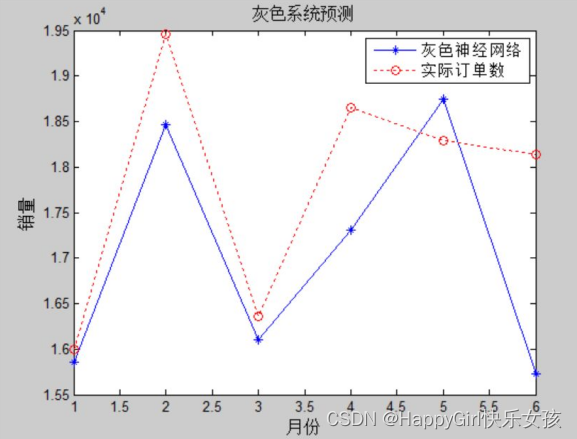
灰色神经网络预测用网络预测订单数量，并根据预测误差判断网络性能。

共有过去3年36个月的数据，首先取前30个月的数据作为训练数据训练网络，网络共学习进化100次，然后用剩余6组数据评价网络的预测性能。

灰色神经网络算法程序

%% 清空环境变量
clc
clear

load data

%% 数据累加作为网络输入
[n,m]=size(X);
for i=1:n
    y(i,1)=sum(X(1:i,1));
    y(i,2)=sum(X(1:i,2));
    y(i,3)=sum(X(1:i,3));
    y(i,4)=sum(X(1:i,4));
    y(i,5)=sum(X(1:i,5));
    y(i,6)=sum(X(1:i,6));
end

训练

%% 网络参数初始化
a=0.3+rand(1)/4;
b1=0.3+rand(1)/4;
b2=0.3+rand(1)/4;
b3=0.3+rand(1)/4;
b4=0.3+rand(1)/4;
b5=0.3+rand(1)/4;

%% 学习速率初始化
u1=0.0015;
u2=0.0015;
u3=0.0015;
u4=0.0015;
u5=0.0015;

%% 权值阀值初始化
t=1;
w11=a;
w21=-y(1,1);
w22=2*b1/a;
w23=2*b2/a;
w24=2*b3/a;
w25=2*b4/a;
w26=2*b5/a;
w31=1+exp(-a*t);
w32=1+exp(-a*t);
w33=1+exp(-a*t);
w34=1+exp(-a*t);
w35=1+exp(-a*t);
w36=1+exp(-a*t);
theta=(1+exp(-a*t))*(b1*y(1,2)/a+b2*y(1,3)/a+b3*y(1,4)/a+b4*y(1,5)/a+b5*y(1,6)/a-y(1,1));

kk=1;

02

%% 循环迭代
for j=1:10
%循环迭代
E(j)=0;
for i=1:30
    
%% 网络输出计算
t=i;
LB_b=1/(1+exp(-w11*t));   %LB层输出
LC_c1=LB_b*w21;           %LC层输出
LC_c2=y(i,2)*LB_b*w22;    %LC层输出
LC_c3=y(i,3)*LB_b*w23;    %LC层输出
LC_c4=y(i,4)*LB_b*w24;    %LC层输出
LC_c5=y(i,5)*LB_b*w25;    %LC层输出
LC_c6=y(i,6)*LB_b*w26;    %LC层输出
    LD_d=w31*LC_c1+w32*LC_c2+w33*LC_c3+w34*LC_c4+w35*LC_c5+w36*LC_c6;    %LD层输出
    theta=(1+exp(-w11*t))*(w22*y(i,2)/2+w23*y(i,3)/2+w24*y(i,4)/2+w25*y(i,5)/2+w26*y(i,6)/2-y(1,1));   %阀值
    ym=LD_d-theta;   %网络输出值
    yc(i)=ym;
    
    %% 权值修正
    error=ym-y(i,1);      %计算误差
    E(j)=E(j)+abs(error);    %误差求和       
    error1=error*(1+exp(-w11*t));     %计算误差
    error2=error*(1+exp(-w11*t));     %计算误差
    error3=error*(1+exp(-w11*t));
    error4=error*(1+exp(-w11*t));
    error5=error*(1+exp(-w11*t));
    error6=error*(1+exp(-w11*t));
    error7=(1/(1+exp(-w11*t)))*(1-1/(1+exp(-w11*t)))*(w21*error1+w22*error2+w23*error3+w24*error4+w25*error5+w26*error6);
    
    %修改权值
    w22=w22-u1*error2*LB_b;
    w23=w23-u2*error3*LB_b;
    w24=w24-u3*error4*LB_b;
    w25=w25-u4*error5*LB_b;
    w26=w26-u5*error6*LB_b;
    w11=w11+a*t*error7;
end
end  

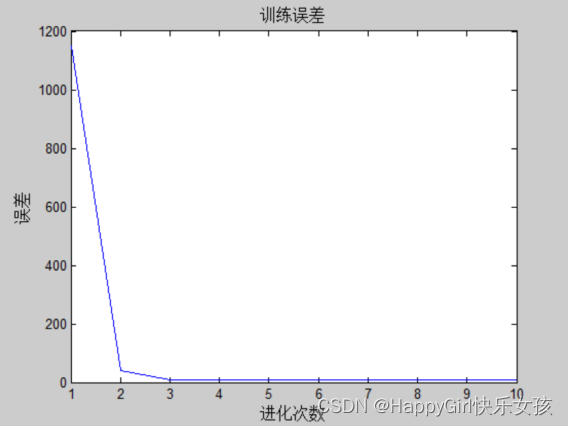
%画误差随进化次数变化趋势
figure(1)
plot(E)
title('训练误差','fontsize',12);
xlabel('进化次数','fontsize',12);
ylabel('误差','fontsize',12);
%print -dtiff -r600 28-3

%根据训出的灰色神经网络进行预测
for i=31:36
    t=i;
    LB_b=1/(1+exp(-w11*t));   %LB层输出
    LC_c1=LB_b*w21;           %LC层输出
    LC_c2=y(i,2)*LB_b*w22;    %LC层输出
    LC_c3=y(i,3)*LB_b*w23;    %LC层输出
    LC_c4=y(i,4)*LB_b*w24;    %LC层输出
    LC_c5=y(i,5)*LB_b*w25;
    LC_c6=y(i,6)*LB_b*w26;
    LD_d=w31*LC_c1+w32*LC_c2+w33*LC_c3+w34*LC_c4+w35*LC_c5+w36*LC_c6;    %LD层输出
    theta=(1+exp(-w11*t))*(w22*y(i,2)/2+w23*y(i,3)/2+w24*y(i,4)/2+w25*y(i,5)/2+w26*y(i,6)/2-y(1,1));   %阀值
    ym=LD_d-theta;   %网络输出值
    yc(i)=ym;
end
yc=yc*100000;
y(:,1)=y(:,1)*10000;

仿真结果图

源码链接：

 基于BP的神经网络变量筛选matlab源码.rar-Matlab文档类资源-CSDN文库