199. 二叉树的右视图【111】网站首页 技术杂谈

199. 二叉树的右视图【111】

Java大数据运动猿 2023-07-09 08:00:03

简介199. 二叉树的右视图【111】

难度等级：中等

上一篇算法：

236. 二叉树的最近公共祖先【190】

力扣此题地址：

199. 二叉树的右视图 - 力扣（Leetcode）

1.题目：199. 二叉树的右视图

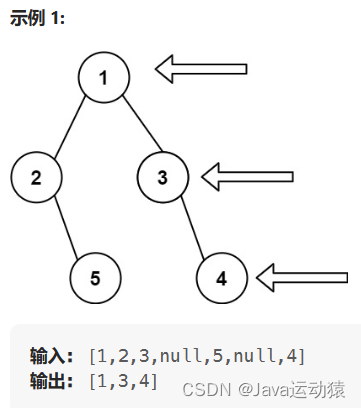
给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

2.解题思路：

DFS：

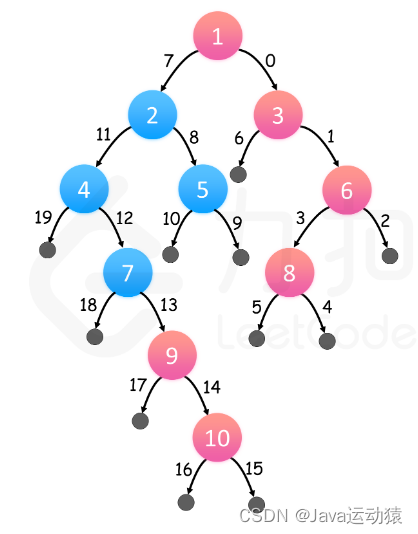
既然是站在右边看树，那么我们看到的结点都是每一层的最右边的结点，这个节点可能在根的右子树上，也可能在根的左子树上。

所以，我们可以递归遍历树，使用深度优先算法，按照【根节点 ->右子树 -> 左子树】的顺序访问。

同时设置一个depth变量，如果depth的值与res集合中的元素数量相等的话，就说明当前被遍历到的这个节点没有放在res中，所以将这个节点的值放到res中，同时每遍历一层就加一，这样就能知道树的深度，也可以保证每一层只有一个节点可以放入res中，这样就可以保证每层都是最先访问最右边的结点的。

（因为先遍历右子树，右子树上的每一层的最右边节点都放入了res中，当右子树遍历完成之后，回过来开始遍历左子树，depth会从头开始计算值，那么已经遍历过的层数会从头开始算，然而res中已经加入了右子树的值，所以当depth的值 != res.size()的时候，就说明这一层已经有了值在res中）

如果还是不理解的话，可以看看代码辅助理解，这张图也可以清晰地展示出思路：

思路参考：

199. 二叉树的右视图 - 力扣（Leetcode）

199. 二叉树的右视图 - 力扣（Leetcode）

BFS：

广度优先的思路：我们可以设置一个堆，然后分别将每一层的结点的值放入堆中，每一层取堆顶的元素即可，堆顶元素就是一层中最右边的结点的值。可以模仿层次遍历。

3.代码实现：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
 //DFS深度优先算法
class Solution {
    //先创建一个list集合存储数据作为返回
    List<Integer> res = new ArrayList<Integer>();

    public List<Integer> rightSideView(TreeNode root) {
        //传入根节点root，以及depth = 0
        dfs(root,0);
        return res;
    }

    public void dfs(TreeNode root,int depth){
        //先判断，如果根节点为null则返回，同时也是递归的终止条件，访问到叶子结点的下一个的时候为null，则返回
        if(root == null){
            return;
        }

        //先访问当前结点，再递归地访问右子树 和 左子树
        if(depth == res.size()){//如果当前结点所在深度还没有出现在res里，说明在该深度下，当前结点是第一个被访问的结点（按照我们给定的思路规则也是当前深度下的最右边的结点），因此将当前结点加入res中
            res.add(root.val);
        }
        //每递归一次就说明走到下一层，depth++
        depth++;

        //先递归右子树，再递归左子树，这样每一层都能访问到最右边的结点
        dfs(root.right,depth);
        dfs(root.left,depth);
    }
}