• CSDN个人主页：清风莫追
• 欢迎关注本专栏：《一起撸个DL框架》
• GitHub获取源码：https://github.com/flying-forever/OurDL

5 实现：自适应线性单元🍇

1 简介

上一篇：【一起撸个DL框架】4 反向传播求梯度

上一节我们实现了计算图的反向传播，可以求结果节点关于任意节点的梯度。下面我们将使用梯度来更新参数，实现一个简单的自适应线性单元。

我们本次拟合的目标函数是一个简单的线性函数：$y=2x+1$，通过随机数生成一些训练数据，将许多组x和对应的结果y值输入模型，但是并不告诉模型具体函数中的系数参数“2”和偏置参数“1”，看看模型能否通过数据“学习”到参数的值。

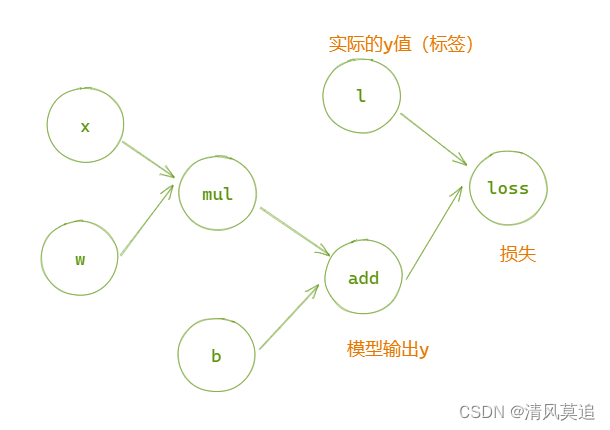图1：自适应线性单元的计算图

2 损失函数

2.1 梯度下降法

损失是对模型好坏的评价指标，表示模型输出结果与正确答案（也称为标签）之间的差距。所以损失值越小就说明模型越准确，训练过程的目的便是最小化损失函数的值。

自适应线性单元是一个回归任务，我们这里将使用绝对值损失，将模型输出与正确答案之间的差的绝对值作为损失函数的值，即$loss=|l-add|$。

评价指标有了，可是如何才能达标呢？或者说如何才能降低损失函数的值？计算图中有四个变量：$x,w,b,l$，而我们训练过程的任务是调整参数$w,b$的值，以降低损失。因此训练过程中的自变量是w和b，而把x和l看作常量。此时损失函数是关于w和b的二元函数$loss=f(w,b)$，我们只需要求函数的梯度$▽f(w,b)=(\frac{\partial f}{\partial w},\frac{\partial f}{\partial b})$，则梯度的反方向就是函数下降最快的方向。沿着梯度的方向更新参数w和b的值，就可以降低损失。这就是经典的优化算法：梯度下降法。

2.2 补充

关于损失和优化的概念，大家可能还是有些模糊。上面损失只讲到了一个输入x值对应的模型输出与实际结果之间的差距，但使用整个数据集的平均差距可能更容易理解，就像中学的线性回归。

如图2所示，改变直线的斜率w，将改变直线与数据点的贴近程度，即改变了损失函数loss的值。

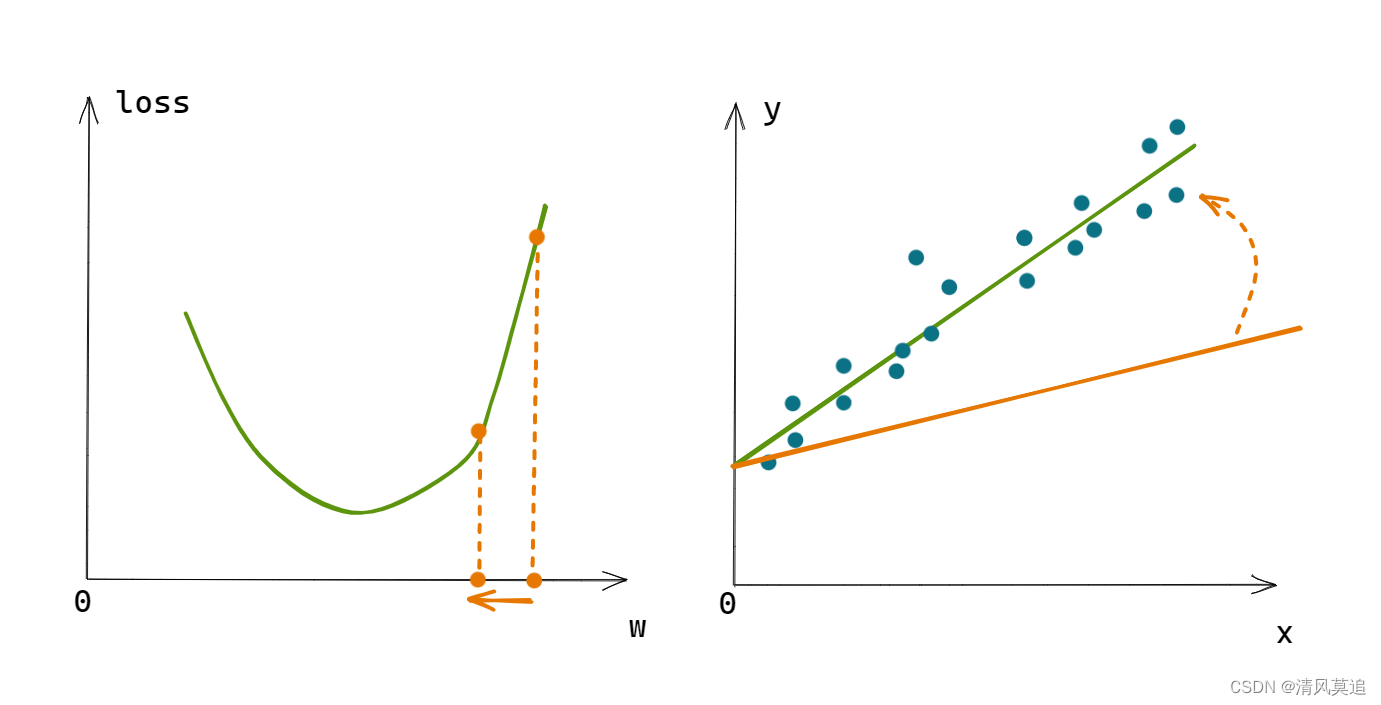图2：损失与参数更新示意图

参考: 【深度学习】3-从模型到学习的思路整理_清风莫追的博客-CSDN博客

3 整理项目结构

我们的小项目的代码也渐渐多起来了，好的目录结构将使它更加易于扩展。关于python包结构的知识大家可以自行去了解，大致目录结构如下：

- example
- ourdl
	- core
		- __init__.py
		- node.py
	- ops
		- __init__.py
		- loss.py
		- ops.py
	__init__.py

给这个简单框架的名字叫做OurDL，使用框架搭建的计算图等程序放在example目录下。在ourdl/core/node.py中存放了节点基类和变量类的定义，在ourdl/ops/下存放了运算节点的定义，包括损失函数和加法、乘法节点等。

4 损失函数的实现

在/ourdl/ops/loss.py中，

from ..core import Node

class ValueLoss(Node):
    '''损失函数：作差取绝对值'''
    def compute(self):
        self.value = self.parent1.value - self.parent2.value
        self.flag = self.value > 0
        if not self.flag:
            self.value = -self.value
    def get_parent_grad(self, parent):
        a = 1 if self.flag else -1
        b = 1 if parent == self.parent1 else -1
        return a * b

其中compute()方法很显然就是对两个输入作差取绝对值；get_parent_grad()方法求本节点关于父节点的梯度。有绝对值如何求梯度？大家可以画一画绝对值函数的图像。

5 修改节点类（Node）

在ourdl/core/node.py，

class Node:
    pass  # 省略了一些方法的定义，大家可以查看上一篇文章

    def clear(self):
        '''递归清除父节点的值和梯度信息'''
        self.grad = None
        if self.parent1 is not None:  # 清空非变量节点的值
            self.value = None
        for parent in [self.parent1, self.parent2]:
            if parent is not None:
                parent.clear()
    def update(self, lr=0.001):
        '''根据本节点的梯度，更新本节点的值'''
        self.value -= lr * self.grad  # 减号表示梯度的反方向

我在节点类中新增了两个方法，其中clear()用于清除多余的节点值和梯度信息，因为当节点值或梯度已经存在时会直接返回结果而不会递归去求了（见get_grad()和forward()的代码）。update()有一个学习率参数lr，更新幅度太大可能导致参数值一直在目标值左右晃悠，无法收敛。

6 自适应线性单元

在/example/01_esay/自适应线性单元.py，

import sys
sys.path.append('../..')
from ourdl.core import Varrible
from ourdl.ops import Mul, Add
from ourdl.ops.loss import ValueLoss

if __name__ == '__main__':
    # 搭建计算图
    x = Varrible()
    w = Varrible()
    mul = Mul(parent1=x, parent2=w)
    b = Varrible()
    add = Add(parent1=mul, parent2=b)
    label = Varrible()
    loss = ValueLoss(parent1=label, parent2=add)
    # 参数初始化
    w.set_value(0)
    b.set_value(0)
    # 生成训练数据
    import random
    data_x = [random.uniform(-10, 10) for i in range(10)]  # 按均匀分布生成[-10, 10]范围内的随机实数
    data_label = [2 * data_x_one + 1 for data_x_one in data_x]
    # 开始训练
    for i in range(len(data_x)):
        x.set_value(data_x[i])
        label.set_value(data_label[i])
        loss.forward()  # 前向传播 --> 求梯度会用到损失函数的值
        w.get_grad()
        b.get_grad()
        w.update(lr=0.05)
        b.update(lr=0.1)
        loss.clear()
        print("w:{:.2f}, b:{:.2f}".format(w.value, b.value))
    print("最终结果：{:.2f}x+{:.2f}".format(w.value, b.value))
    

运行结果：

w:0.13, b:0.10
w:0.36, b:0.20
w:0.58, b:0.10
w:0.74, b:0.00
w:1.13, b:0.10
w:1.43, b:0.20
w:1.62, b:0.30
w:1.94, b:0.20
w:1.50, b:0.30
w:1.87, b:0.40
最终结果：1.87x+0.40

上面自适应线性单元的训练，已经能够大致展现深度学习模型的训练流程：

• 搭建模型 --> 初始化参数 --> 准备数据 --> 使用数据更新参数的值

我们这里参数只更新了10次，结果就已经大致接近了我们的目标函数$y=2x+1$。大家可以试试更改学习率lr，训练数据集的大小，观察运行结果会发生怎样的变化。（必备技能：调参)

下节预告：激活函数与计算图的非线性拟合能力