您现在的位置是：首页 >其他 >【超算/先进计算学习】日报6网站首页其他

【超算/先进计算学习】日报6

鱼树(◔◡◔) 2023-06-28 16:00:02
简介【超算/先进计算学习】日报6

目录

今日已完成任务列表

4-3、传统性能优化

遇到的问题及解决方案

无

任务完成详细笔记

传统性能优化

从体系结构角度理解四种计算优化途径-主频/缓存/流水线/超标量

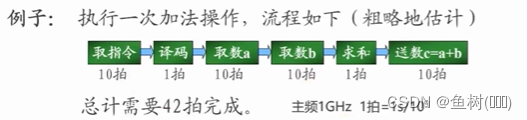
在这里插入图片描述
提高计算速度的技术途径：
1、提高主频
2、高速缓冲存储器
3、流水线技术
4、并行技术

  • 提高主频
    与硬件制造工艺有关
  • 高速缓存
    降低数据传输过程中的花费
  • 流水线技术
    同一周期多条指令 (不相互冲突) 重叠执行
  • 并行技术
    例如：存在多个加法部件

优化途径的有效适用条件

  • 提高主频
    在非理想情况下，运算速度与主频不成比例增长
  • 高速缓存
    经常出现缓存缺失的情况，需要找的数据不在高速缓存中 (缓存不命中)
  • 流水线技术
    当数据之间存在相关性时，并不能保持流水线指令的流水执行
  • 并行技术
    并性结果正在输出时会导致并行中断
    充分利用流水、并行工作的条件

指令间没有相关，即相互独立
结构相关：两条指令要用同一个部件
数据相关：一条指令要用另一条指令的结果
控制相关：条件转移指令影响其他指令

存储墙与层次式存储结构

在这里插入图片描述

  • CPU消耗数据的速率远大于存储器供数率

时钟频率增长的速度远大于访存时间缩短的速度
同时执行多条指令要求供数率进一步提高
多线程或芯片内多处理器要求访问多组数据

  • 已知的解决方案：存储器层次结构

片内 cache 的供数率能满足指令级并行的要求
片内 cache 的命中率足够高
为多个线程或处理器提供各自的 cache
如何通过程序或算法的改进增强访存的局部性

数据局部性与cache

  • 时间局部性
    指的是同一份数据在短时间内往往会被多次重复使用，例如：当我们读取了一个数据 a，在接下来一段时间可能会不断地访问数据 a
  • 空间局部性
    指的是如果访问了某个数据，那么往往也需要访问它附近的数据，例如：如果访问了一个数组里的元素 a[1]，那么接下来很有可能会访问 a[0] 或 a[2]
    cache 结构
    在这里插入图片描述
  • 一个一个的 cacheline 堆叠而成
    当前顺序的 cache 命中率至少 75%
  • cache 满了之后的替换
    整行替换 cacheline
    间隔访问数据容易导致 cache miss

循环合并

  • loop fusion，将具有相同迭代次序的两个循环合并成一个
for (i=0; i<N; i++)
	x[i] = a[i] + b[i]
for (i=0; i<N; i++)
	y[i] = a[i] - b[i]

for (i=0; i<N; i++)
{
	x[i] = a[i] + b[i];
	y[i] = a[i] - b[i];
}
  • 优点
    减少循环迭代的开销
    增强数据重用，寄存器重用
    减小并行化的启动开销

进行循环合并后不能影响最终的程序运行结果

循环展开

  • loop unrolling，是一种牺牲程序长度来加快程序执行速度的方法。可以由程序原完成，也可以由编译器完成。
    在这里插入图片描述
for (i=0; i<N; i++)
{
	A[i] = A[i] + B[i];
}

for (i=0; i<N; i+=4)
{
	A[i] = A[i] + B[i];
	A[i+1] = A[i+1] + B[i+1];
	A[i+2] = A[i+2] + B[i+2];
	A[i+3] = A[i+3] + B[i+3];
}
  • 优点
    减少循环指令分支的次数
    获得更多的指令级并行
    增加了寄存器的重用

循环交换

当一个循环体中包含一个以上的循环，且循环语句之间不包含其他语句，则称这个循环为紧嵌套循环，交换紧嵌套中两个循环的嵌套顺序是提高程序性能最有效的变换之一。实际上，循环交换是一个重排序变换，仅改变了参数化迭代的执行顺序，但是并没有删除任何语句或产生任何新的语句，所以循环交换的合法性需要通过循环的依赖关系进行判定。

for (j=0; j<N; j++)
{
	for (k=0; k<N; k++)
	{
		for (i=0; i<N; i++)
		{
			A[i][j] = a[i][j] + B[i][k] * C[k][j];
		}
	}
}

for (j=0; j<N; j++)
	for (i=0; i<N; i++)
		for (k=0; k<N; k++)
			A[i][j] = A[i][j] + B[i][k] * C[k][j];
  • 优点
    增强数据局部性
    增强向量化和并行化的识别

循环分布

  • Loop Distribute，是指将一个循环分解为多个循环，且每个循环都有与原循环相同的迭代空间，但只包含原循环的语句子集，常用于分解出可向量化或者可并行化的循环，进而将可向量化部分的代码转为向量执行
for (i=0; i<N; i++)
{
	A[i] = i;
	B[i] = 2 + B[i];
	C[i] = 3 + C[i-1];
}

for (i=0; i<N; i++)
{
	A[i] = i;
	B[i] = 2 + B[i];
}
for (i=0; i<N; i++)
	C[i] = 3 + C[i-1];
  • 优点
    将串行循环转变为多个并行循环
    实现循环的部分并行化
    增加循环的优化范围
  • 缺点
    减小了并行粒度，增加了额外的通信和同步开销

循环不变量外提

  • 循环不变量是指在迭代过程中不发生变化的量。由于不发生变化，可以将循环不变量提到循环外面，避免重复计算
for (i=0; i<N; i++)
	for (j=0; j<M; j++)
		U[i] = U[i] + W[i] * W[i] * D[j] / (dt * dt);

T1 = dt * dt;
for (i=0; i<N; i++)
{
	T2 = W[i] * W[i];
	for (j=0; j<M; j++)
		U[i] = U[i] + T2 * D[j]/T1;
}
  • 优点
    减小循环内的计算量

循环分块

  • 思路：一个 cache line 现在被用过以后，后面什么时候还会被用，按照循环默认的执行方式，可能到下次再被用到的时候已经被替换了。于是我们就把循环重排一下，使得一个 cache line 在被替换之前就被再次使用
    在这里插入图片描述
  • A[i] 在每一轮 j 循环中被重用
  • B[j] 当 M 数值比较大时，无法全部缓存在 cache 里。所以当 i 进入到下一层循环时，B[0] 已经被清出 cache，无法重用
  • 假设 cache line 大小为 b。理想情况下，则可计算出 A 的 cache miss 次数是 N/b，B 的 cache miss 次数是 N*M/b
    在这里插入图片描述
  • 分块 j 层循环，将 B 的访问模式变成如下，令块大小为 T，T 一般是 b 的倍数，也足够小，可以认为 N，M>>b, T，T 的取值应该使得当 B(T) 被访问时 B(0) 也依然还在缓存中
  • 分块 j 层循环的时候，分块后 j 层循环变到了外面，该操作会影响 A 的缓存命中率。A 的 cache miss 次数：(M/T) x (N/b)，B 的 cache miss 次数是 T/b x M/T = M/b

矩阵乘法
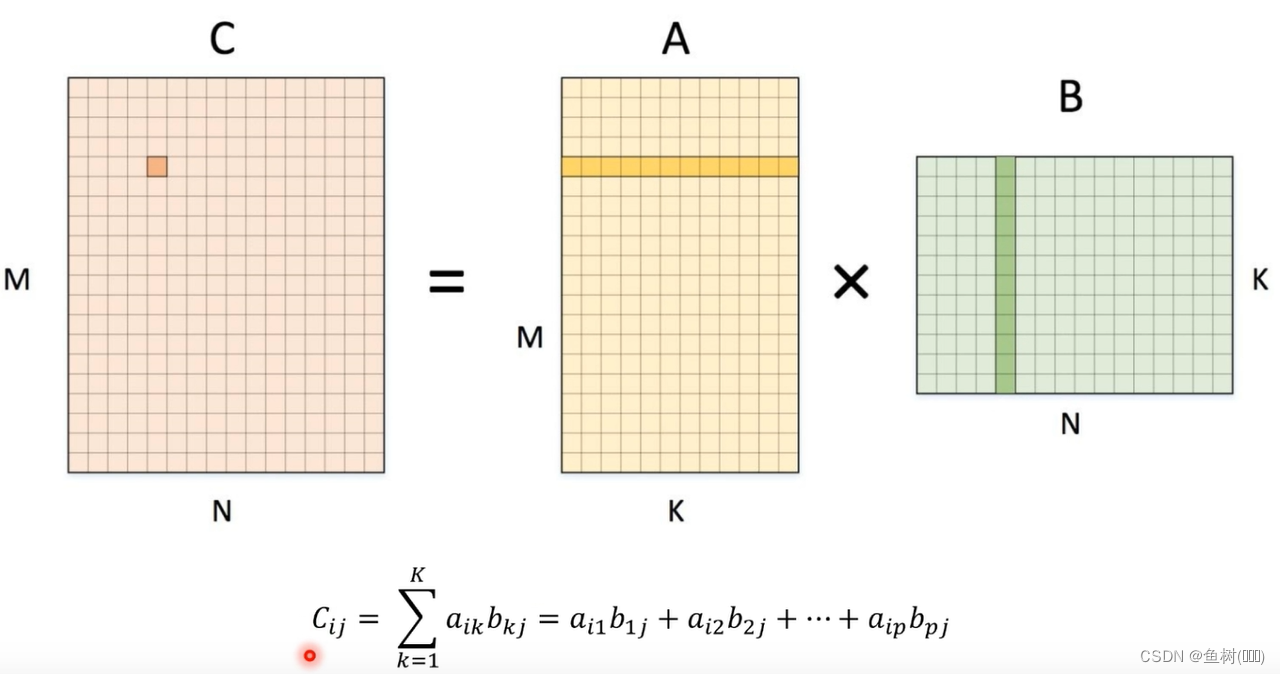
在这里插入图片描述
矩阵分块算法可以提高缓存的命中率
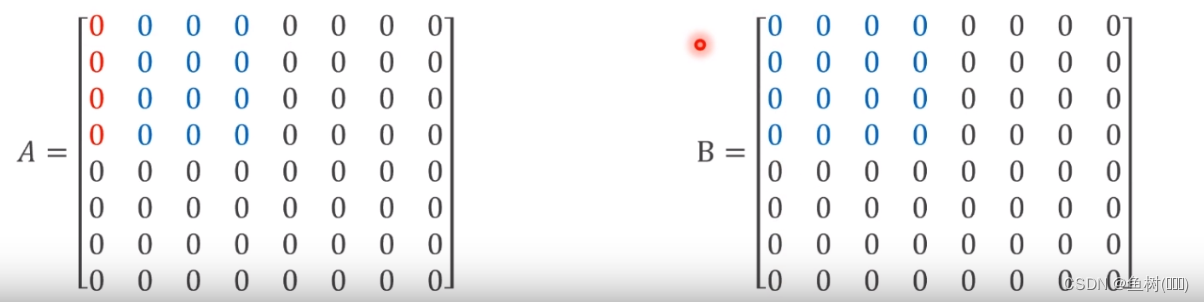
在这里插入图片描述

inline void do_block(int n, float *A, float *B, float *C)
{
	for (int i=0; i<BLOCKSIZE; i++)
	{
		for (int j=0; j<BLOCKSIZE; j++)
		{
			float cij = C[i*n + j];
			for (int k=0; k<BLOCKSIZE; k++)
			{
				cij += A[i*n + k] * B[k*n + j];  // C[i][j] = A[i][:] * B[:][j]
			}
			C[i*n + j] = cij;
		}
	}
}
inline void degmm_block(int n, float *A, float *B, float *C)
{
	for (int sj=0; sj<n; sj += BLOCKSIZE)              
		for (int si=0; si<n; si += BLOCKSIZE)
			for (int sk=0; sk<n; sk += BLOCKSIZE)
				do_block(n, A + si*n + sk, B + sk*n + sj, C + si*n +sj);
}

分块要点
1、根据矩阵大小选择是否分块
2、处理不能整除的情况
3、保证计算结果的正确性
4、基于不同矩阵大小测试不同块大小对性能的影响

循环分裂

  • 循环分裂是将循环的迭代次数拆成两段或者多段，拆分后的循环不存在主体循环之说，也就是拆分成迭代次数都比较多的两个或者多个循环
for (i=0; i<N; i++)
	vec[i] = vec[i] + vec[M];

for (i=0; i<M; i++)
	vec[i] = vec[i] + vec[M];
for (i=M; i<N; i++)
	vec[i] = vec[i] + vec[M];
  • 优点
    增加编译器向量化可能 -O3 -fopt-info

优化 jacobi 程序

  • 未采用任何优化手段
    在这里插入图片描述
    根据上次的分析，程序的热点函数为 LaplasEquationSolver，所以重点考虑对其进行优化
  • 进行循环展开
	do {
		for (uint8_t i = 1; i < N - 1; ++i){
			for (uint8_t j = 1; j < K - 1; j+=2) {
				u1[i][j] = (1.0 / 4.0) * (u1[i - 1][j] + u1[i + 1][j] + u1[i][j - 1] + u1[i][j + 1]);	
				u1[i][j+1] = (1.0 / 4.0) * (u1[i - 1][j+1] + u1[i + 1][j+1] + u1[i][j] + u1[i][j + 2]);	
			}
		}

		for (uint8_t i = 1; i < N - 1; ++i){
			for (uint8_t j = 1; j < K - 1; j+=2) {
				u2[i][j] = (1.0 / 4.0) * (u1[i - 1][j] + u1[i + 1][j] + u1[i][j - 1] + u1[i][j + 1]);
				u2[i][j+1] = (1.0 / 4.0) * (u1[i - 1][j+1] + u1[i + 1][j+1] + u1[i][j] + u1[i][j + 2]);
			}
		}

		for (uint8_t i = 0; i < N; ++i){
			for (uint8_t j = 0; j < K; j+=2) {
				u_new[i][j] = u1[i][j] + w * (u2[i][j] - u1[i][j]);
				u_new[i][j+1] = u1[i][j+1] + w * (u2[i][j+1] - u1[i][j+1]);
			}
		}

		for (uint8_t i = 0; i < N; ++i) {
			for (uint8_t j = 0; j < K; j+=2) {
				errors.push_back(fabs(u_new[i][j] - u1[i][j]));
				errors.push_back(fabs(u_new[i][j+1] - u1[i][j+1]));
			}
		}
		max_error = *std::max_element(errors.begin(), errors.end());
		//if(k%100==0)std::cout<<k<<" "<<max_error<<"
";
		errors.clear();
		for (uint8_t i = 0; i < N; ++i) {
			for (uint8_t j = 0; j < K; j+=2) {
				u1[i][j] = u_new[i][j];
				u1[i][j+1] = u_new[i][j+1];
			}
		}
		k++;
	} while (max_error > eps);

在这里插入图片描述

  • 进行循环合并
	do {
		for (uint8_t i = 1; i < N - 1; ++i) {
			for (uint8_t j = 1; j < K - 1; ++j) {
				u1[i][j] = (1.0 / 4.0) * (u1[i - 1][j] + u1[i + 1][j] + u1[i][j - 1] + u1[i][j + 1]);
			}
		}
		for (uint8_t i = 1; i < N - 1; ++i) {
			for (uint8_t j = 1; j < K - 1; ++j) {
				u2[i][j] = (1.0 / 4.0) * (u1[i - 1][j] + u1[i + 1][j] + u1[i][j - 1] + u1[i][j + 1]);
			}
		}
		for (uint8_t i = 0; i < N; ++i) {
			for (uint8_t j = 0; j < K; ++j) {
				u_new[i][j] = u1[i][j] + w * (u2[i][j] - u1[i][j]);
				errors.push_back(fabs(u_new[i][j] - u1[i][j]));;
				u1[i][j] = u_new[i][j];
			}
		}
		max_error = *std::max_element(errors.begin(), errors.end());
		//if(k%100==0)std::cout<<k<<" "<<max_error<<"
";
		errors.clear();
		k++;
	} while (max_error > eps);

在这里插入图片描述

  • 进行循环分裂
	do {
		for (uint8_t i = 1; i < N - 1; ++i) {
			for (uint8_t j = 1; j < 101; ++j) {
				u1[i][j] = (1.0 / 4.0) * (u1[i - 1][j] + u1[i + 1][j] + u1[i][j - 1] + u1[i][j + 1]);
			}
			for (uint8_t j = 101; j < K - 1; ++j) {
				u1[i][j] = (1.0 / 4.0) * (u1[i - 1][j] + u1[i + 1][j] + u1[i][j - 1] + u1[i][j + 1]);
			}
		}
		for (uint8_t i = 1; i < N - 1; ++i) {
			for (uint8_t j = 1; j < 101; ++j) {
				u2[i][j] = (1.0 / 4.0) * (u1[i - 1][j] + u1[i + 1][j] + u1[i][j - 1] + u1[i][j + 1]);
			}
			for (uint8_t j = 101; j < K - 1; ++j) {
				u2[i][j] = (1.0 / 4.0) * (u1[i - 1][j] + u1[i + 1][j] + u1[i][j - 1] + u1[i][j + 1]);
			}
		}
		for (uint8_t i = 0; i < N; ++i) {
			for (uint8_t j = 0; j < 100; ++j) {
				u_new[i][j] = u1[i][j] + w * (u2[i][j] - u1[i][j]);
			}
			for (uint8_t j = 100; j < K; ++j) {
				u_new[i][j] = u1[i][j] + w * (u2[i][j] - u1[i][j]);
			}
		}
		for (uint8_t i = 0; i < N; ++i) {
			for (uint8_t j = 0; j < 100; ++j) {
				errors.push_back(fabs(u_new[i][j] - u1[i][j]));;
			}
			for (uint8_t j = 100; j < K; ++j) {
				errors.push_back(fabs(u_new[i][j] - u1[i][j]));;
			}
		}
		max_error = *std::max_element(errors.begin(), errors.end());
		//if(k%100==0)std::cout<<k<<" "<<max_error<<"
";
		errors.clear();
		for (uint8_t i = 0; i < N; ++i) {
			for (uint8_t j = 0; j < 100; ++j) {
				u1[i][j] = u_new[i][j];
			}
			for (uint8_t j = 100; j < K; ++j) {
				u1[i][j] = u_new[i][j];
			}
		}
		k++;
	} while (max_error > eps);

在这里插入图片描述

  • 循环交换+循环合并+循环展开

这里进行循环分裂与不进行循环分裂效果似乎差不多

	do {
		for (uint8_t i = 1; i < N - 1; ++i) {
			for (uint8_t j = 1; j < 101; j+=2) {
				u1[i][j] = (1.0 / 4.0) * (u1[i - 1][j] + u1[i + 1][j] + u1[i][j - 1] + u1[i][j + 1]);
				u1[i][j+1] = (1.0 / 4.0) * (u1[i - 1][j+1] + u1[i + 1][j+1] + u1[i][j] + u1[i][j + 2]);
			}
			for (uint8_t j = 101; j < K - 1; j+=2) {
				u1[i][j] = (1.0 / 4.0) * (u1[i - 1][j] + u1[i + 1][j] + u1[i][j - 1] + u1[i][j + 1]);
				u1[i][j+1] = (1.0 / 4.0) * (u1[i - 1][j+1] + u1[i + 1][j+1] + u1[i][j] + u1[i][j + 2]);
			}
		}
		for (uint8_t i = 1; i < N - 1; ++i) {
			for (uint8_t j = 1; j < 101; j+=2) {
				u2[i][j] = (1.0 / 4.0) * (u1[i - 1][j] + u1[i + 1][j] + u1[i][j - 1] + u1[i][j + 1]);
				u2[i][j+1] = (1.0 / 4.0) * (u1[i - 1][j+1] + u1[i + 1][j+1] + u1[i][j] + u1[i][j + 2]);
			}
			for (uint8_t j = 101; j < K - 1; j+=2) {
				u2[i][j] = (1.0 / 4.0) * (u1[i - 1][j] + u1[i + 1][j] + u1[i][j - 1] + u1[i][j + 1]);
				u2[i][j+1] = (1.0 / 4.0) * (u1[i - 1][j+1] + u1[i + 1][j+1] + u1[i][j] + u1[i][j + 2]);
			}
		}
		for (uint8_t i = 0; i < N; ++i) {
			for (uint8_t j = 0; j < 100; j+=2) {
				u_new[i][j] = u1[i][j] + w * (u2[i][j] - u1[i][j]);
				u_new[i][j+1] = u1[i][j+1] + w * (u2[i][j+1] - u1[i][j+1]);
				errors.push_back(fabs(u_new[i][j] - u1[i][j]));;
				errors.push_back(fabs(u_new[i][j+1] - u1[i][j+1]));;
				u1[i][j] = u_new[i][j];
				u1[i][j+1] = u_new[i][j+1];
			}
			for (uint8_t j = 100; j < K; j+=2) {
				u_new[i][j] = u1[i][j] + w * (u2[i][j] - u1[i][j]);
				u_new[i][j+1] = u1[i][j+1] + w * (u2[i][j+1] - u1[i][j+1]);
				errors.push_back(fabs(u_new[i][j] - u1[i][j]));;
				errors.push_back(fabs(u_new[i][j+1] - u1[i][j+1]));;
				u1[i][j] = u_new[i][j];
				u1[i][j+1] = u_new[i][j+1];
			}
		}
		max_error = *std::max_element(errors.begin(), errors.end());
		//if(k%100==0)std::cout<<k<<" "<<max_error<<"
";
		errors.clear();
		k++;
	} while (max_error > eps);

在这里插入图片描述

对自己的表现是否满意

最近对传统性能优化的一些方法进行了学习，了解了传统性能优化的原理 (与计算机体系结构和缓存的关系)，通过这些优化方法程序的执行效率确实得到了显著的提高，是非常重要且实用的技术。

简述下次计划

Darknet 项目优化

其他反馈

无

风语者！平时喜欢研究各种技术，目前在从事后端开发工作，热爱生活、热爱工作。

站长推荐