您现在的位置是:首页 >其他 >软考算法-排序篇-上网站首页其他
软考算法-排序篇-上
数据排序
一:故事背景
最近在准备5月底的软件工程师的考试,这个考试最困难的就是算法部分了。接下来的文章我将会总结 排序与算法,希望通过此系列文章的总结,能让我们不但把握住考试的试题,更可以学会分析算法,写出优秀的算法,优化我们的代码。
二:直接插入排序
2.1 概念
- 在插入第 i 个记录时,R1,R2,…Ri-1 都已经排好序。这时候将第 i 个记录依次与 Ri-1 … R2,R1 进行比较,找到合适的位置插入,插入位置及之后的记录依次向后移动
2.2 画图表示
只看概念描述可能不是很好理解,让我们来画图理解一下,这个算法。
- 首先给出一组待排序的数字

- 根据上述概念,我们必须从第二个开始进行排序,因为第一个数据之前没有数据,对第一个数据比价是没有意义的。
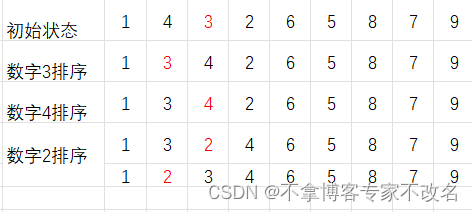
通过观察规律和结合概念描述,我们可以看出。整个顺序是前面的部分,逐渐有序的。那个数据需要排序,那么它之前的数据一定是有序的。例如:数字4排序前,它前面的数字为 1,3,是有序的, 数字2排序前,它前面的数字为 1,3,4是有序的,根据以上规律依次类推就可以将数据进行从小到大排序
2.3 代码实现
上文给出了对应算法的图,相信通过此图,大家对直接插入算法有了一定的了解,那让我们来看看,如何用代码去实现直接插入算法吧
- 算法代码
public static void insertionSort(int[] nums) {
//首先记录数组的长度
int len = nums.length;
//从数组的第二个元素开始
for (int i = 1; i < len; i++) {
//依次取出一个元素,存储在current变量中
Integer current = nums[i];
//定义一个指针,初始化当前元素的前一个位置
int j = i - 1;
//重复上述操作,直到找到一个位置j,使得 nums[j] <= current,或者 j 已经到达数组的起始位置。
while (j >= 0 && nums[j] > current) {
nums[j + 1] = nums[j];
j--;
}
nums[j + 1] = current;
}
}
- 执行代码
public class Main {
public static void main(String[] args) {
int[] nums = {1,4, 3, 2,6,5,8,7,9};
System.out.println("排序前"+Arrays.toString(nums));
Sort1.insertionSort(nums);
System.out.println("排序后"+Arrays.toString(nums));
}
}
- 运行结果

上述代码中核心点有两个:
- 一个是循环的边界。
外层for循环的边界是从第二个元素开始,到最后一个循环结束。
内层的while循环的边界是到第一个数据并且找到的数据必须比当前操作的数据大。 - 一个是数据的交换。
数据交换主要体现在内层的while循环中,如果符合条件则将比当前 j指针标记的数向后移动一个。最后找到符合条件的位置时,将当前操作的数 current 放到指定位置。
2.4 总结提升
上述给出了直接插入排序的算法分析与实例。直接插入排序算法在最好情况下(数据完全有序)时间复杂度为O(n),最坏的情况下(数据无序)为O(n²)。此算法属于比较简单的算法。希望大家通过我的博客能够理解此算法。
三:希尔排序
3.1 概念
- 希尔排序又称“缩小增量排序”,他是对“直接插入排序的改进”。
- 希尔排序的思想是:先将整个待排记录分割成若干个子序列,然后分别进行直接插入排序,待整个序列中的记录基本有序时,再对全体进行一次直接插入排序。
3.2 画图表示
希尔排序的核心点是:** 分隔子序列 **,将待排数组分割成子序列,分别进行排序。具体的分隔数没有特别要求,一般初始值是待排数列的一半,然后依次减半,直至最后间隔为1为止。

上图中,给出了一个待排数组的变化。
- 待排数组长度为8,所以子序列间隔分别为 4 2 1
- 间隔为4时,一共有4组数据,将这四组数据进行直接插入排序,保证这四组数据有序。
- 间隔为2时,一共有2组数据,将这两组数据进行直接插入排序,保证这两组数据有序。
- 间隔为1时,整体进行直接插入排序,但是这时数据已经基本有序,需要移动的数据很少。
3.3 代码实现
下文给出** 希尔排序** 的具体实现:
public static void shellSort(int[] arr) {
//交换的次数
int num = 0;
int n = arr.length;
// 初始化增量gap为数组长度的一半
for (int gap = n / 2; gap > 0; gap /= 2) {
System.out.println("gap值" + gap);
// 对于每个增量gap,进行一次插入排序
for (int i = gap; i < n; i++) {
//temp表示当前操作的元素
int temp = arr[i];
//j是一个指针,表示当前操作的元素
int j = i;
// 对于每个元素,向前比较gap个距离的元素。如果前面的元素大于当前元素才需要交换
while (j >= gap && arr[j - gap] > temp) {
//后面元素挪到前面
arr[j] = arr[j - gap];
//当前操作元素变为前gap个
j -= gap;
}
//将本次需要操作元素放到移动的位置
arr[j] = temp;
num++;
System.out.println(gap + Arrays.toString(arr));
}
}
System.out.println("一共交换了:"+ num +"次");
}
3.4 总结提升
希尔排序是一种不稳定的排序算法。其时间复杂度约为O(n¹·³),在排序过程中需要一个元素的辅助空间用于元素值交换,空间爱你复杂的为O(1)。
相对于直接插入排序而言,希尔排序的时间复杂度更低,效率更高,对于大规模数据排序更加适用。
四:直接选择排序
4.1 概念
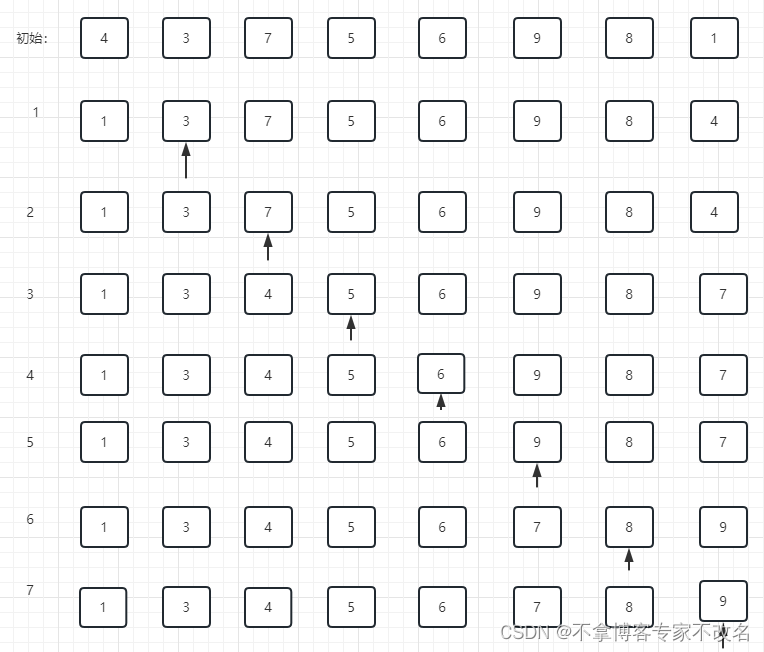
直接选择排序是一种简单排序算法,它的基本思想是:在待排的数据中选取最小值,与当前值进行交换,直至交换完毕。
4.2 画图表示
4.3 代码实现
/**
* @BelongsProject: algorithm
* @BelongsPackage: org.example
* @Author:hlzs1
* @Description: 直接选择排序
* @CreateTime: 2023-04-28 10:44
* @Version: 1.0
*/
public class Sort3 {
public static void SelectionSort(int[] arr) {
int length = arr.length;
for (int i = 0; i < length-1 ; i++) {
//从当然开始筛选
int minIndex = i;
for (int j = i+1; j < length; j++) {
if(arr[minIndex] >arr[j]){
minIndex = j;
}
}
//交换数值
int current = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = current;
}
}
}
4.4 总结提升
- 直接选择排序的时间复杂度为 O(n^2),其中 n 是待排序数组的长度。具体来说,它的时间复杂度由两个嵌套循环决定。
- 直接选择排序的时间复杂度为 O(n^2),其中 n 是待排序数组的长度。具体来说,它的时间复杂度由两个嵌套循环决定。
五:堆排序
5.1 概念
- 在计算机科学中,堆(Heap)是一种特殊的树形数据结构,它通常是一个近似完全二叉树,其中父节点的值总是大于或小于它的子节点。具体而言,堆被分为两种类型:最大堆(Max Heap)和最小堆(Min Heap)。
- 在最大堆中,每个节点的值都大于或等于其子节点的值。因此,最大堆的根节点是堆中的最大元素。在最小堆中,每个节点的值都小于或等于其子节点的值。因此,最小堆的根节点是堆中的最小元素。
5.1.1 堆
5.1.2 堆排序
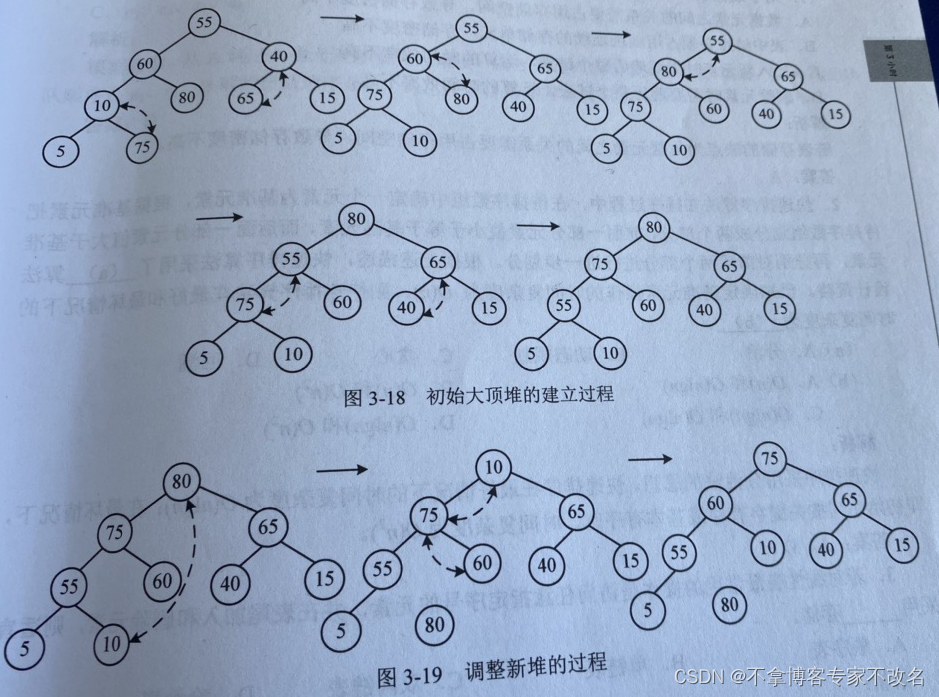
- 对一组待排序元素,首先按照堆的定义排成一个序列(建立初始堆),之后输出堆顶最大元素(对于大顶堆而言)
- 然后将剩余的元素在调整成新堆,从而得到次大元素,如此反复,直到全部元素有序为止。
5.2 画图表示
5.3 代码实现
public static void heapSort(int[] arr) {
//判断如果arr为空或者只有一个数据,则不需要进行排序
if (arr == null || arr.length < 2) {
return;
}
//构建大根堆
for (int i = 0; i < arr.length; i++) {
heapInsert(arr, i);
}
//将堆顶元素依次放到数组最后,并重新调整堆结构
int size = arr.length;
swap(arr, 0, --size);
while (size > 0) {
heapify(arr, 0, size);
swap(arr, 0, --size);
}
}
//构建大根堆
public static void heapInsert(int[] arr, int index) {
//如果
while (arr[index] > arr[(index - 1) / 2]) {
swap(arr, index, (index - 1) / 2);
index = (index - 1) / 2;
}
}
//调整大根堆
public static void heapify(int[] arr, int index, int size) {
int left = index * 2 + 1;
while (left < size) {
int largest = left + 1 < size && arr[left + 1] > arr[left] ? left + 1 : left;
largest = arr[largest] > arr[index] ? largest : index;
if (largest == index) {
break;
}
swap(arr, largest, index);
index = largest;
left = index * 2 + 1;
}
}
//交换数组中的两个元素
public static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
//测试
public static void main(String[] args) {
int[] arr = {4, 6, 2, 9, 1, 8, 5, 3, 7};
heapSort(arr);
System.out.println(Arrays.toString(arr));
}
5.4 总结提升
堆排序是一种不稳定的排序,与直接插入排序很像,每次都是筛选出一个最值,但是不同的是,堆排序利用了树的结构,进行了排序。
六:表格比较
| 算法名 比较项 | 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|
| 直接插入排序 | O(n) ~ O(n²) | O(1) | 稳定 |
| 希尔排序 | 约为O(n¹·³) | O(1) | 不稳定 |
| 直接选择排序 | O(n²) | O(1) | 稳定 |
| 堆排序 | O(nlogn) | O(1) | 不稳定 |
七:总结&提升
本文给出了直接插入排序、希尔排序、直接选择排序、堆排序的。概念、图、和代码。希望大家通过此篇文章能理解什么是算法,各个算法的不同作用,这对我们以后看源码,自己编写代码有很大的好处,可以很好的训练我们的思维。
本篇为上篇,接下来的文章,我会继续输出关于数据排序的另外四种算法,有兴趣的朋友请持续关注我~





 U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... SpringSecurity实现前后端分离认证授权
SpringSecurity实现前后端分离认证授权