前言

如果你不太了解dp（动态规划）是个什么东西，请回到上次dp。

链接：动态规划算法详解

数字三角形模型

问题 A: 【一本通基础DP基础模型】【例9.2】数字金字塔

【题目描述】

观察下面的数字金字塔。写一个程序查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以从当前点走到左下方的点也可以到达右下方的点。

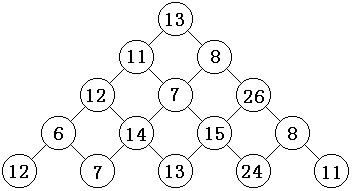
在上面的样例中,从13到8到26到15到24的路径产生了最大的和86。

【输入】

第一个行包含R(1≤ R≤1000)，表示行的数目。

后面每行为这个数字金字塔特定行包含的整数。

所有的被供应的整数是非负的且不大于100。

【输出】

单独的一行，包含那个可能得到的最大的和。

【输入样例】

5
13
11 8
12 7  26
6  14 15 8
12 7  13 24 11

【输出样例】

86

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1005;
int a[MAXN][MAXN], f[MAXN][MAXN], n;
int main() {
    //读入 
    cin >> n;
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= i; j++)
        {
            cin >> a[i][j];
        }
    }
    //初始化 
    f[1][1] = a[1][1];
    //随时更新f[i][j] 
    for(int i = 2; i <= n; i++) {
        for(int j = 1; j <= i; j++) {
            f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + a[i][j];
        }
    }
    int ans = 0;
    //比较ans和f[n][i]
    for(int i = 1; i <= n; i++) {
        ans = max(ans, f[n][i]);
    }
    cout << ans << endl;
    return 0;
} 

最长上升子序列模型

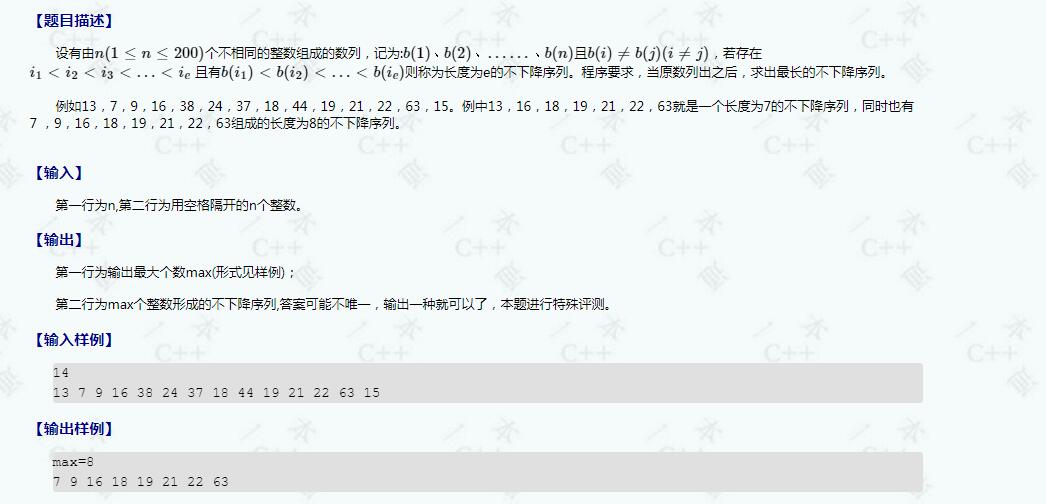
【例9.3】求最长不下降序列

[题目描述]

#include <bits/stdc++.h>
using namespace std;
const int N = 1001;
int a[N], f[N], c[N];
int main() {
    int n, maxx = -23333333;
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    int k;
    for (int i = 1; i <= n; i++) {
        f[i] = 1;
        for (int j = 1; j < i; j++) {
            if (a[j] <= a[i] && f[j] + 1 > f[i])
                f[i] = f[j] + 1;
        }
        if (f[i] > maxx) {
            maxx = f[i];
            k = i;
        }
    }
    int q = 0, m = maxx, i = k - 1;
    c[q++] = k;
    while (m > 1) {
        if (f[i] == m - 1 && a[i] <= a[k]) {
            c[q++] = i;
            k = i;
            m--;
        }
        i--;
    }
    printf("max=%d", maxx);
    cout << endl;
    for (int i = q - 1; i >= 0; i--) printf("%d ", a[c[i]]);
    return 0;
}

背包模型

423. 采药

辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。

为此，他想拜附近最有威望的医师为师。

医师为了判断他的资质，给他出了一个难题。

医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同的草药，采每一株都需要一些时间，每一株也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”

如果你是辰辰，你能完成这个任务吗？

输入格式

输入文件的第一行有两个整数 T和 M，用一个空格隔开，T代表总共能够用来采药的时间，M 代表山洞里的草药的数目。

接下来的 M 行每行包括两个在 1 到 100 之间（包括 1 和 100）的整数，分别表示采摘某株草药的时间和这株草药的价值。

输出格式

输出文件包括一行，这一行只包含一个整数，表示在规定的时间内，可以采到的草药的最大总价值。

数据范围

1≤T≤1000,
1≤M≤100

输入样例：

70 3
71 100
69 1
1 2

输出样例：

3

#include <bits/stdc++.h>
using namespace std;
 
int dp[10010];
int money[101];
int shijian[101];
int t, shumu;
 
int main()
{
    scanf("%d%d", &t, &shumu);
    for(int i = 1; i <= shumu; i++)
    {
        scanf("%d%d", &shijian[i], &money[i]);
    }
    for(int i = 1; i <= shumu; i++)
    {
        for(int j = t; j >= shijian[i]; j--)
        {
            if(dp[j] < dp[j - shijian[i]] + money[i])
            {
                dp[j] = dp[j - shijian[i]] + money[i];
            }
        }
    }
    printf("%d", dp[t]);
    return 0;
}

状态机模型

1049. 大盗阿福

阿福是一名经验丰富的大盗。趁着月黑风高，阿福打算今晚洗劫一条街上的店铺。

这条街上一共有 N 家店铺，每家店中都有一些现金。

阿福事先调查得知，只有当他同时洗劫了两家相邻的店铺时，街上的报警系统才会启动，然后警察就会蜂拥而至。

作为一向谨慎作案的大盗，阿福不愿意冒着被警察追捕的风险行窃。

他想知道，在不惊动警察的情况下，他今晚最多可以得到多少现金？

输入格式

输入的第一行是一个整数 T，表示一共有 T 组数据。

接下来的每组数据，第一行是一个整数 N ，表示一共有 N 家店铺。

第二行是 N 个被空格分开的正整数，表示每一家店铺中的现金数量。

每家店铺中的现金数量均不超过1000。

输出格式

对于每组数据，输出一行。

该行包含一个整数，表示阿福在不惊动警察的情况下可以得到的现金数量。

数据范围

1≤T≤50
1≤N≤105

输入样例：

2
3
1 8 2
4
10 7 6 14

输出样例：

8
24

样例解释

对于第一组样例，阿福选择第2家店铺行窃，获得的现金数量为8。

对于第二组样例，阿福选择第1和4家店铺行窃，获得的现金数量为10+14=24。

#include <bits/stdc++.h>
using namespace std;
#define read(a) scanf("%d", &a);
const int N = 1e5 + 10, INF = 1e9;
int t, n;
int w[N], f[N][2];
int main() {
	read(t);
	while(t--) {
		read(n);
		for(int i = 1; i <= n; i++) read(w[i]);
		f[0][0] = 0, f[0][1] = -INF;
		for(int i = 1; i <= n; i++) {
			f[i][0] = max(f[i - 1][0], f[i - 1][1]);
			f[i][1] = f[i - 1][0] + w[i];
		}
		printf("%d
", max(f[n][1], f[n][0]));
	}
	return 0;
}

还有以下内容没有更新，敬请期待：

1.背包模型

2.状态机模型

3.状态压缩DP

4.区间DP

5.树形DP

6.数位DP

7.单调队列优化DP

8.斜率优化DP