【Unity入门】三维向量

    大家好，我是Lampard~~

    欢迎来到Unity入门系列博客，所学知识来自B站阿发老师~感谢 

（一）空间向量

（1）什么是三维向量

    为什么会有这么一篇博客呢？主要是三维向量在unity中扮演者重要的角色，很多组件的参数用到的类型都是Vector3类型

    如果各位看官们，此时正在读大学，或者刚出校门。那可以直接跳过，你们掌握的知识绝对比我要好。这篇文章主要用于给像博主这种离开校园已久的小社畜们，起到一个回顾作用

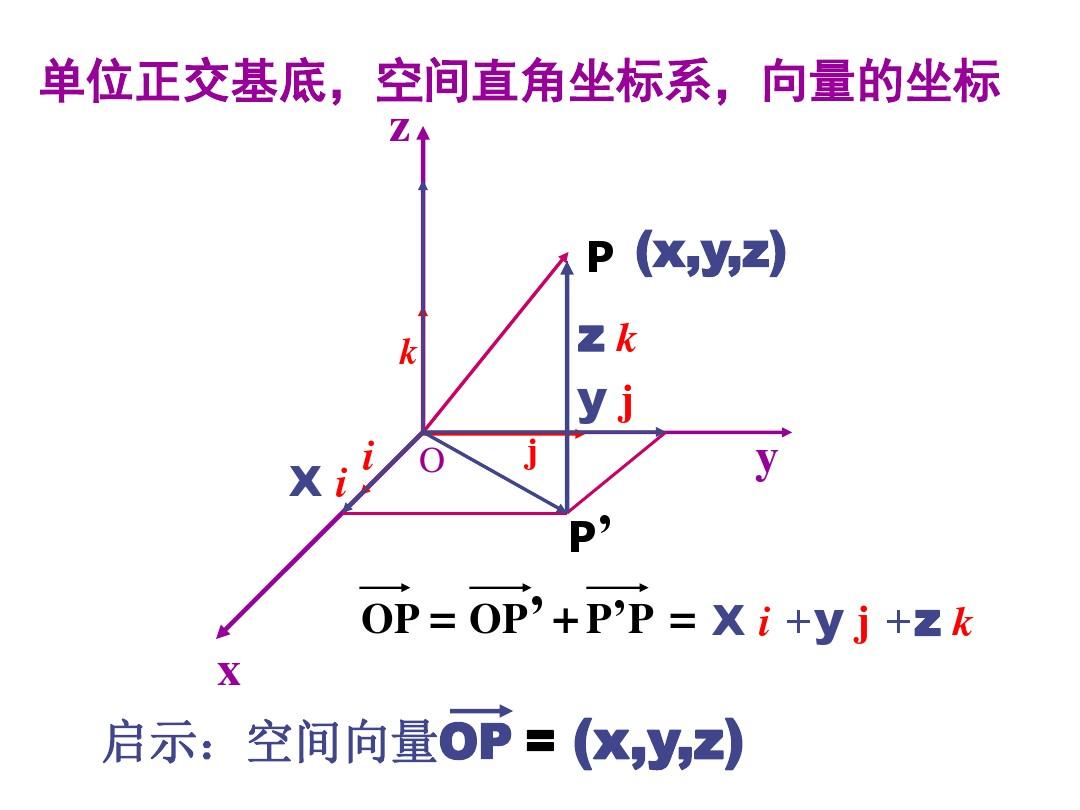
    如图所示三维向量是指在三维空间中具有大小和方向的向量，通常用三个实数表示，分别代表向量在 X、Y、Z 三个轴上的分量

    在Unity中我们有用到vector3类型，最常见的，就是我们的transform组件

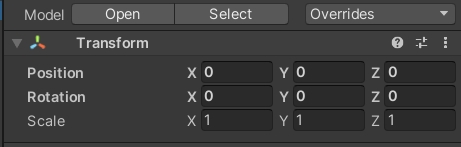
（2）向量的加减法

    从数字上看加减法很简单，比如向量（3,0,0） + （0,4,0）,得出的结果就是（3,4,0）

    同样的向量（3,4,0） 减去向量（3,0,0）就得出（0,4,0），向量的各个部分自己相加减

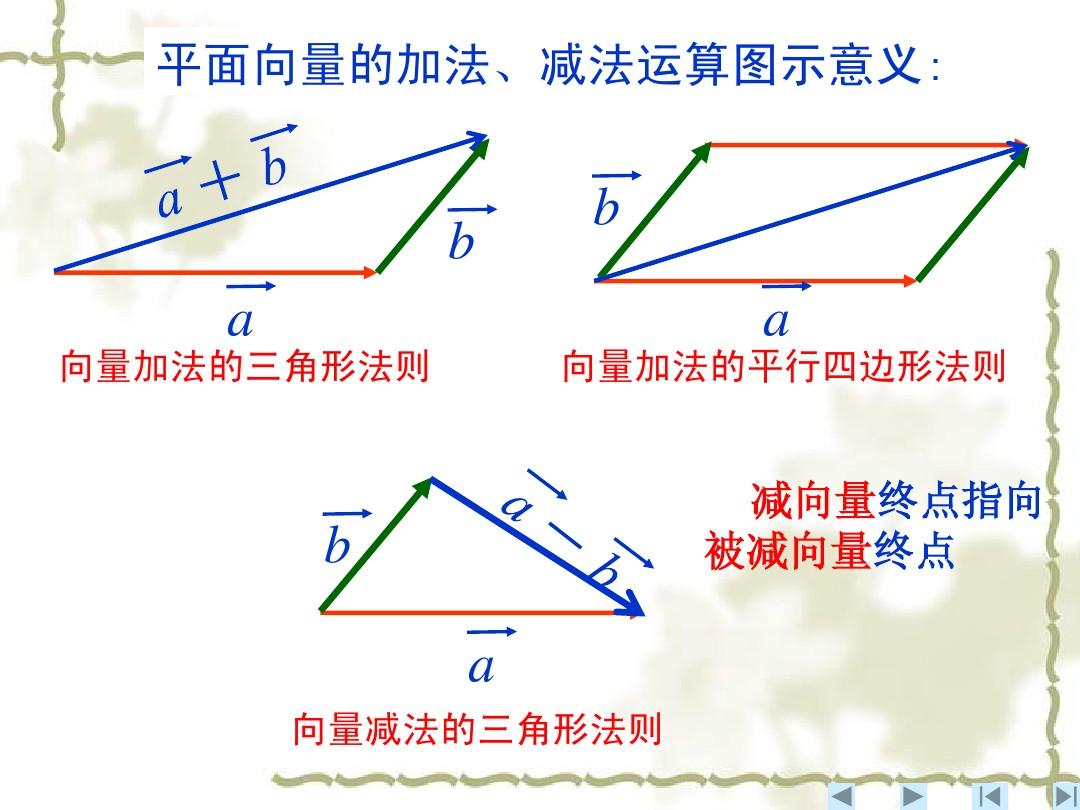
     从图形上来看，向量相加可以通过三角形定理或者平行四边形定理，得出一个新的向量。而向量相减，则可以用来计算两个向量之间的距离

（3）向量的长度

    向量怎么求长度呢？很简单就是x²+y²+z²开根号

     比如，向量（3,4,0）的长度就是5啦，接下来会引入一个单位向量的概念

单位向量是指一个长度为1的向量，也称为标准向量或归一化向量。在三维几何中，单位向量在表示方向时非常有用，因为它们只描述方向，而无需考虑大小或缩放

    那么对于（3,4,0）向量来说，它的向量就是（0.6,0.8,0）了

（4）向量的点乘

    前面的内容还比较简单，到了点乘和叉乘的时候，大家就可以开始迷糊了，开始头皮发痒（死去的记忆突然攻击我）

    向量的点乘（又称为数量积或内积）是一种向量运算，它将两个向量的对应分量相乘，再将结果相加，得到一个标量（即一个实数）

    公式如下：

a · b = a.x * b.x + a.y * b.y + a.z * b.z

其中 a 和 b 都是三维向量，a.x, a.y, a.z 分别表示向量 a 在 X、Y、Z 轴上的分量，b.x, b.y, b.z 同理

    比如（3,0,0）点乘（0,4,0）= 0，那点乘有啥作用呢？

    比如我们可以同点乘来判定两个向量是否垂直，若向量A点乘向量B = 0则代表两个向量垂直；可以用来计算两个向量的角度：cos θ = (a · b) / (||a|| * ||b||)，和向量在另一向量的投影等

（5）向量的叉乘

    叉乘应该是大一高数学习的？哈哈哈真的忘了

向量的叉乘（又称为向量积或外积）是一种向量运算，它将两个向量的对应分量进行计算得到一个新向量，新向量的方向与原两个向量垂直，大小等于原两个向量构成的平行四边形的面积

    其计算公式如下图，其中i，j，k是xyz的单位向量：

    叉乘有啥用呢？我们可以计算出垂直于这两个向量的法向量，以及可以利用它判定一个点是不是在几何图形内部等

（二）unity向量相关接口

（1）向量的加减法

    unity给我们提供了很多接口方便我们使用，其中加减就没啥好说的，直接计算就行：

Vector3 aaa = new Vector3(3,0,0);
Vector3 bbb = new Vector3(0,4,0);
Debug.Log("向量aaa + 向量bbb = " + (aaa + bbb));
Debug.Log("向量aaa - 向量bbb = " + (aaa - bbb));

    输出如下：

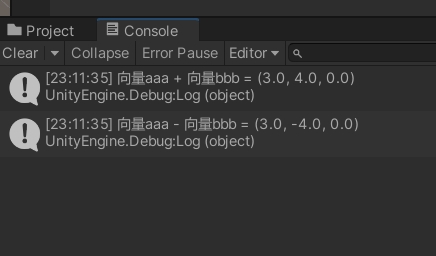
（2）向量的长度magnitude

    unity的Vector3类给我们提供了一个magnitude的方法，可以输出长度：

Debug.Log("向量aaa + 向量bbb的长度为 = " + (aaa + bbb).magnitude);

    输出如下：

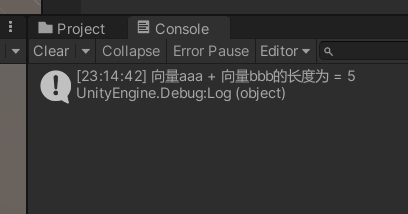
（3）单位向量normalized

    我们还可以对向量进行单位化，就是把向量的方向不变，长度转化成1.使用到的接口是normalized

Debug.Log("向量aaa + 向量bbb的单位向量为 = " + (aaa + bbb).normalized);

    输出如下：

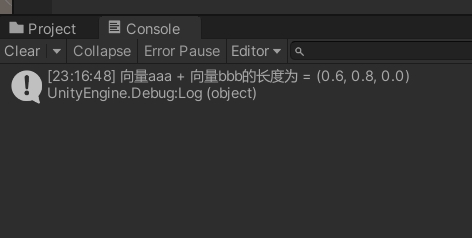
    Vector3还提供了几个单位向量的常量，如下我们可以直接使用： 

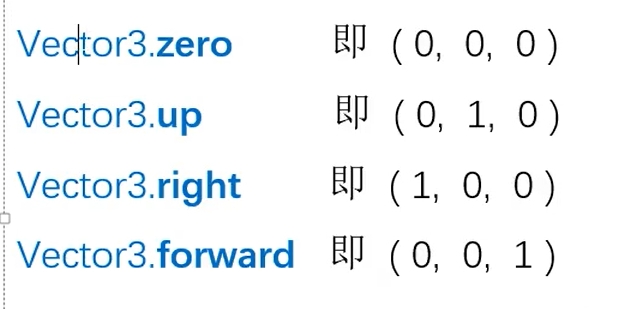
（4）向量的点乘Dot

    点乘可以用Vector3的静态方法，Dot

Vector3 aaa = new Vector3(3,0,0);
Vector3 bbb = new Vector3(0,4,0);
Debug.Log("向量aaa 点乘 向量bbb的结果 = " + Vector3.Dot(aaa, bbb));

    输出如下：

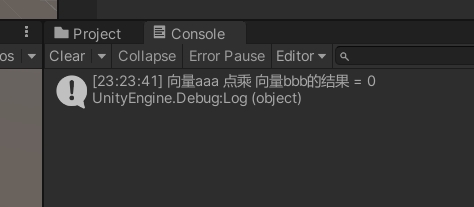
（5）向量的叉乘Cross

    叉乘可以用Vector3的静态方法，Cross

Vector3 aaa = new Vector3(3,0,0);
Vector3 bbb = new Vector3(0,4,0);
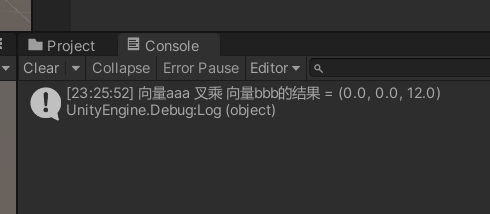
Debug.Log("向量aaa 叉乘 向量bbb的结果 = " + Vector3.Cross(aaa, bbb));

    输出如下，一个它们的法向量：

 （6）两个向量的距离

    计算两个向量的距离方式有两种，一个是先向量相减然后再读取magnitude熟悉，另一个可以直接使用Vector3的Distance方法

Vector3 aaa = new Vector3(3,0,0);
Vector3 bbb = new Vector3(0,4,0);
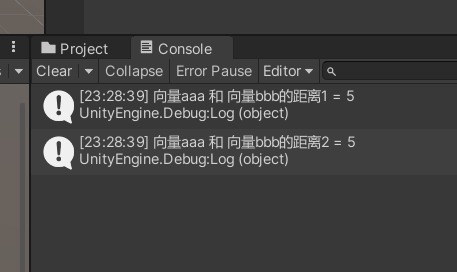
Debug.Log("向量aaa 和 向量bbb的距离1 = " + Vector3.Distance(aaa, bbb));
Debug.Log("向量aaa 和 向量bbb的距离2 = " +(aaa - bbb).magnitude);

    输出如下：

好啦今天就到这里，谢谢各位感谢阅读！！！
点赞，关注！！！