您现在的位置是：首页 >其他 >Top-K问题网站首页其他

Top-K简介

😄Top-k算法常用于对诸如前几名，前几个最大值，前几个最小值这样的问题的求解，并且在数据量较大时力求在最短的时间内求出问题的解。例如：

世界500强公司，世界上年龄最大的几个人，某知名app月度活跃时间最长的几个用户。

😄这些问题的规模以及数据量占比都比较大，如果继续使用排序算法加取值的方式，可能会比较占用资源耗费时间，接下来我们来看下Top-k问题的求解思路：

Top-K算法实现思路

Top-k算法的实现需要借助堆来实现，下面我们一块来由浅入深的实现一下“数组中最小的k个数”的问题的求解过程。

 

😄既然借助堆来实现，那我们可能想：既然求解前k个最小的数，那我直接建一个小根堆，然后依次取出前k个，不就是答案吗？我们来试着实现一下：

import java.util.PriorityQueue;

class Solution {
    public int[] smallestK(int[] arr,int k) {
        int[] res = new int[k];
        //先检验数据的合法性
        if(arr == null || k == 0 || arr.length == k) {
            return res;
        }
        //建立小根堆(PriorityQueue默认是小根堆)
        PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
        for(int i = 0;i < arr.length;i++) {
            priorityQueue.offer(arr[i]);
        }
        //从小根堆中取出k个数据
        for(int i =0;i< k;i++) {
            res[i] = priorityQueue.poll();
        }
        return res;
    }
}

这种解答算法当然没有问题，提交oj也通过测试了。但这并不是top-k问题的解答思路。我们可以发现上面算法的时间负责都为n*log2n，当问题规模比较大时，这种解答方法锁耗费的时间还是相当长的，下面我们来开下top-k问题的正确求解办法：

Top-k问题正确解答思路

• 如果要求前K个最大的数，则建小根堆；
• 如果要求前K个最小的数，则建大根堆；
• 剩余的n-k个数依次与所建堆的堆顶元素进行比较，满足条件时入堆，否则直接跳过，这样就可以实现在时间复杂度为O(N)的情况下解答问题。接下来我们用这种方法来实现一下上面oj中的top-k问题的求解

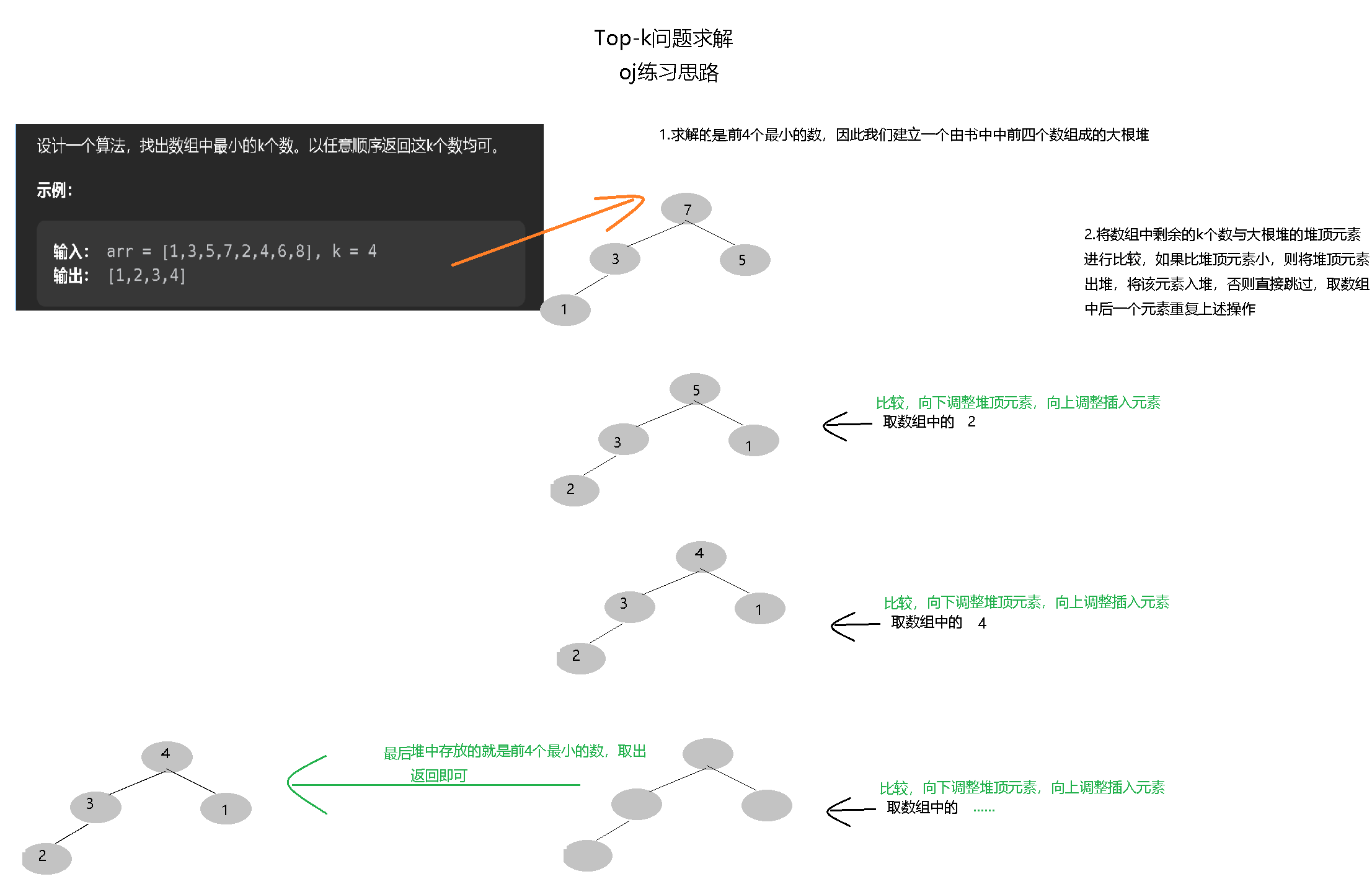
分析上述oj练习：

      题目中要求的是前K个最小的数，根据上面的思路分析，我们可以知道此处应该建立一个大小为K的大根堆；

      假设数组的规模为N，接下来则将剩余的N-K个数依次与大根堆的堆顶元素进行比较；

      大根堆堆顶元素已经是堆中元素的最大值，如果剩余的N-K个元素中比较元素比堆顶元素大，可以说明这个数比堆中的K个数都要大，则跳过继续向后比较，如果这个数比堆顶元素小，则说明这个数是最小的K个数中的一员，那么将堆顶元素出堆，向下调整一次；将比较元素入堆并向上调整一次使堆依然保持大根堆的状态；

      这样一轮进行下来，我们就能够在时间复杂度为O(N)的情况下求解出这个问题：

 

import java.util.PriorityQueue;
import java.util.Comparator;

class Solution {
    public int[] smallestK(int[] arr,int k) {
        int[] res = new int[k];
        //进行形参数据合法性的校验
        if(arr == null || k == 0 || arr.length == k) {
            return res;
        }

        //建立大根堆，将前K个数据元素入堆
        //因为优先级队列的默认建堆种类为小根堆，我们需要在其构造方法中传入比较器让其建立大根堆
        PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(new Comparator<Integer>() {
            public int compare(Integer o1,Integer o2) {
                return o2 - o1;
            }
        });
        for(int i=0;i<k;i++) {
            priorityQueue.offer(arr[i]);
        }
        
        //将剩余的N-k个元素与堆的堆顶元素进行比较，如果比堆顶元素小，则入堆，否则直接跳过
        for(int i=k;i<arr.length;i++) {
            if(priorityQueue.peek() > arr[i]) {
                priorityQueue.poll();
                priorityQueue.offer(arr[i]);
            }
        }
        //取出堆中的K个元素即为求解问题中最小的前K个元素
        for(int i=0;i<k;i++) {
            res[i] = priorityQueue.poll();
        }
        return res;
    }
}