您现在的位置是：首页 >技术交流 >Postgresql逻辑优化学习网站首页技术交流

张树杰优化器原理学习

0 用例

drop table student;
create table student(sno int primary key, sname varchar(10), ssex int);
insert into student values(1, 'stu1', 0);
insert into student values(2, 'stu2', 1);
insert into student values(3, 'stu3', 1);
insert into student values(4, 'stu4', 0);

drop table course;
create table course(cno int primary key, cname varchar(10), tno int);
insert into course values(10, 'meth', 1);
insert into course values(11, 'english', 2);

drop table teacher;
create table teacher(tno int primary key, tname varchar(10), tsex int);
insert into teacher values(1, 'te1', 1);
insert into teacher values(2, 'te2', 0);

drop table score;
create table score (sno int, cno int, degree int);
insert into score values (1, 10, 100);
insert into score values (1, 11, 89);
insert into score values (2, 10, 99);
insert into score values (2, 11, 90);
insert into score values (3, 10, 87);
insert into score values (3, 11, 20);
insert into score values (4, 10, 60);
insert into score values (4, 11, 70);

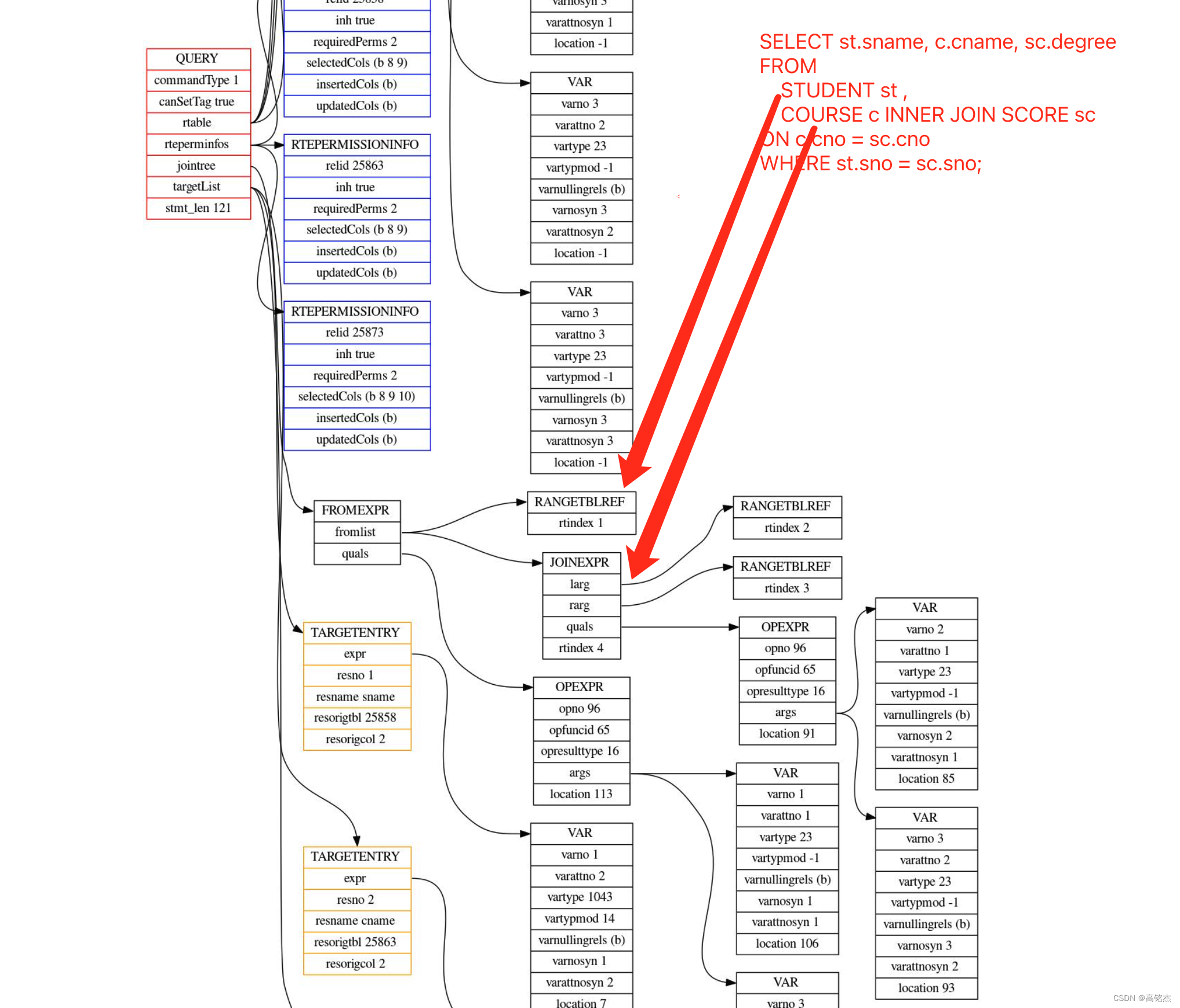
SELECT st.sname, c.cname, sc.degree
FROM STUDENT st ,COURSE c
INNER JOIN SCORE sc
ON c.cno = sc.cno
WHERE st.sno = sc.sno;

1 优化器基础

SQL是描述性语言，对于执行过程没有要求。所以SQL的执行过程是可以充分发挥想象力的：

1. 规则优化、逻辑优化：把SQL对应到逻辑代数的公式，应用一些逻辑代数的等价规则做转换。例如选择下推，子查询提升、外连接消除，都是基于规则的优化，大部分有理论证明优化后的效果更好或至少不会更差，也有一些经验规则。
2. 物理优化：主要是两方面，一个是连接顺序的选择，一个是连接方式的选择。也就是在众多可能得连接路径上，选择一个最优的。
   • 例如客户写出了join a join b join c（a 1MB，b 10GB，c 100GB），那么先连接ab比较好还是bc比较好？显然内连接先连小的比较好，因为结果集会不会超过小表，可以降低后续的连接数量；那么如果join a join b join c where c = 1（a 1MB，b 10GB，c 100GB（c过滤后就剩1kB）），显然应该先执行过滤，过滤后c就变成小表了，应该优先连接c，不但不影响语义，而且会显著降低连接数量。
   • 例如join a join b如果ab表的数据都是有序的，应该选择merge join，如果a表比b表小很多，且b表的连接建选择性非常好，那么使用nestloop会得到性能非常好的执行计划。

2 优化器的输入：查询树

优化器的输入是语义分析的输出：查询树

• 语义分析会严格按照SQL的编写来对应，不会调整任何执行路径。
• 语义分析会检查对象是否存在，并顺便将对象赋予数据库的一些含义，例如将表名对象赋予表的OID等等。

3 逻辑优化

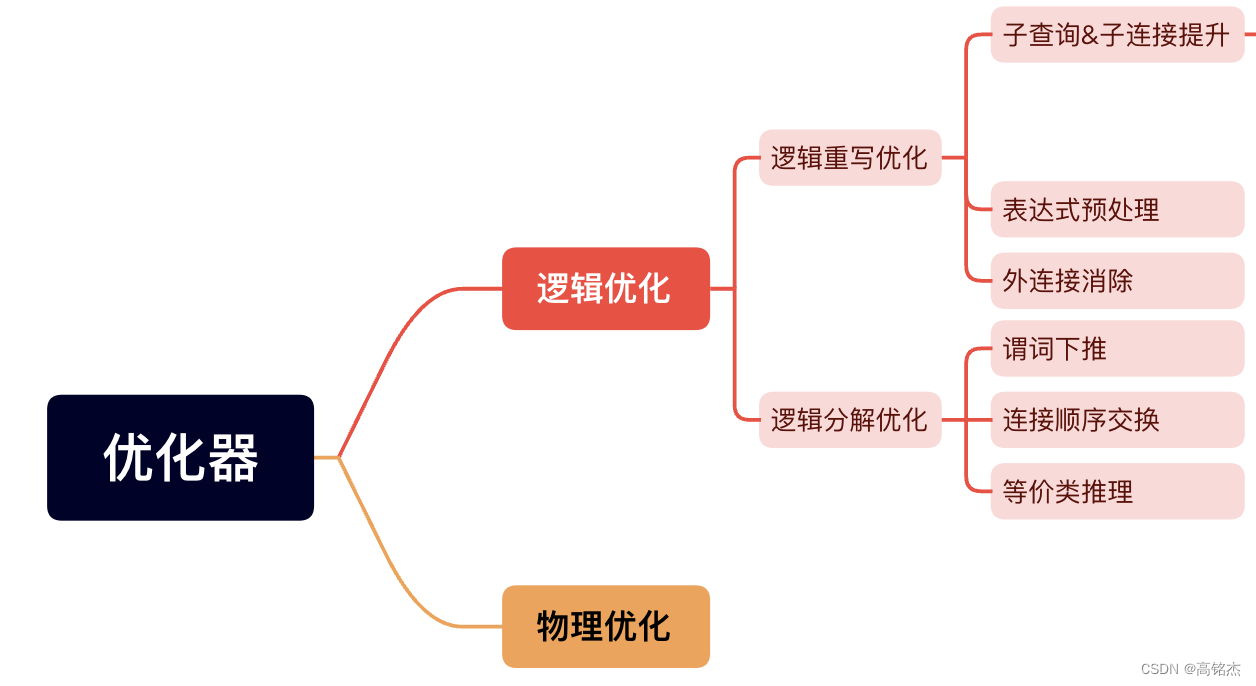
3.1 子查询&子连接提升

Postgresql中通过子句所处的位置来区分子连接和子查询，出现在FROM关键字后的子句是子查询语句，出现在WHERE/ON等约束条件中或投影中的子句是子连接语句：

Postgresql子查询

postgres=# explain SELECT * FROM STUDENT, (SELECT * FROM SCORE) as sc;  
                               QUERY PLAN                               
------------------------------------------------------------------------
 Nested Loop  (cost=0.00..28104.15 rows=2244000 width=58)
   ->  Seq Scan on score  (cost=0.00..30.40 rows=2040 width=12)
   ->  Materialize  (cost=0.00..26.50 rows=1100 width=46)
         ->  Seq Scan on student  (cost=0.00..21.00 rows=1100 width=46)

Postgresql子连接

postgres=# explain SELECT (SELECT AVG(degree) FROM SCORE), sname FROM STUDENT;  
                              QUERY PLAN                               
-----------------------------------------------------------------------
 Seq Scan on student  (cost=35.51..56.51 rows=1100 width=70)
   InitPlan 1 (returns $0)
     ->  Aggregate  (cost=35.50..35.51 rows=1 width=32)
           ->  Seq Scan on score  (cost=0.00..30.40 rows=2040 width=4)

postgres=# explain SELECT * FROM STUDENT WHERE EXISTS (SELECT * FROM SCORE WHERE SCORE.sno = STUDENT.sno); 
                                QUERY PLAN                                 
---------------------------------------------------------------------------
 Hash Join  (cost=40.00..70.01 rows=550 width=46)
   Hash Cond: (student.sno = score.sno)
   ->  Seq Scan on student  (cost=0.00..21.00 rows=1100 width=46)
   ->  Hash  (cost=37.50..37.50 rows=200 width=4)
         ->  HashAggregate  (cost=35.50..37.50 rows=200 width=4)
               Group Key: score.sno
               ->  Seq Scan on score  (cost=0.00..30.40 rows=2040 width=4)

按相关性可以分为相关子连接和非相关子连接：

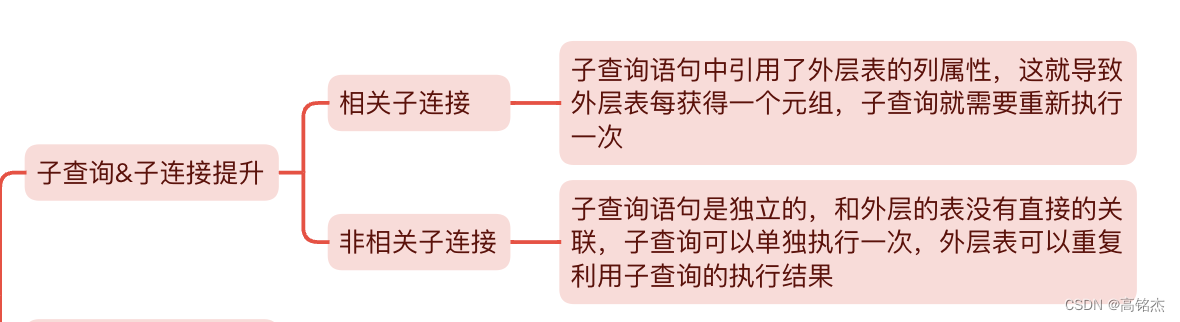
例如：sno实际上产生了一个天然的相关性，这个天然的相关性就会产生嵌套循环，因此是需要提升的

postgres=# explain SELECT * FROM STUDENT WHERE sno > ANY (SELECT sno from STUDENT); 
                                            QUERY PLAN                                             
---------------------------------------------------------------------------------------------------
 Nested Loop Semi Join  (cost=0.15..208.42 rows=367 width=46)
   ->  Seq Scan on student  (cost=0.00..21.00 rows=1100 width=46)
   ->  Index Only Scan using student_pkey on student student_1  (cost=0.15..6.62 rows=367 width=4)
         Index Cond: (sno < student.sno)

子连接是否提升取决于相关性，而这个相关性不只是体现在子句里，也体现在表达式里，也就是说只要能产生嵌套循环，那就有提升的必要。

下面的例子中ANY子查是无法提升的，因为里面的cno和外面的ssex没有相关性，所以会产生subplan。

postgres=# explain SELECT * FROM student WHERE ssex < ANY (SELECT cno FROM score WHERE student.sno = student.sno);  
                              QUERY PLAN                               
-----------------------------------------------------------------------
 Seq Scan on student  (cost=0.00..19551.50 rows=550 width=46)
   Filter: (SubPlan 1)
   SubPlan 1
     ->  Result  (cost=0.00..30.40 rows=2040 width=4)
           One-Time Filter: (student.sno = student.sno)
           ->  Seq Scan on score  (cost=0.00..30.40 rows=2040 width=4)

3.1.1 子连接提升源码分析

explain SELECT sname FROM STUDENT WHERE sno > ANY (SELECT sno FROM SCORE);
                             QUERY PLAN                              
---------------------------------------------------------------------
 Nested Loop Semi Join  (cost=0.00..22497.30 rows=367 width=38)
   Join Filter: (student.sno > score.sno)
   ->  Seq Scan on student  (cost=0.00..21.00 rows=1100 width=42)
   ->  Materialize  (cost=0.00..40.60 rows=2040 width=4)
         ->  Seq Scan on score  (cost=0.00..30.40 rows=2040 width=4)

pull_up_sublinks函数位置

exec_simple_query
  pg_plan_queries
    pg_plan_query                  postgres.c
      planner                      planner.c
        standard_planner           planner.c
          	subquery_planner       planner.c
          	  pull_up_sublinks     prepjointree.c   

GDB挂到函数上，先打印下当前的查询树

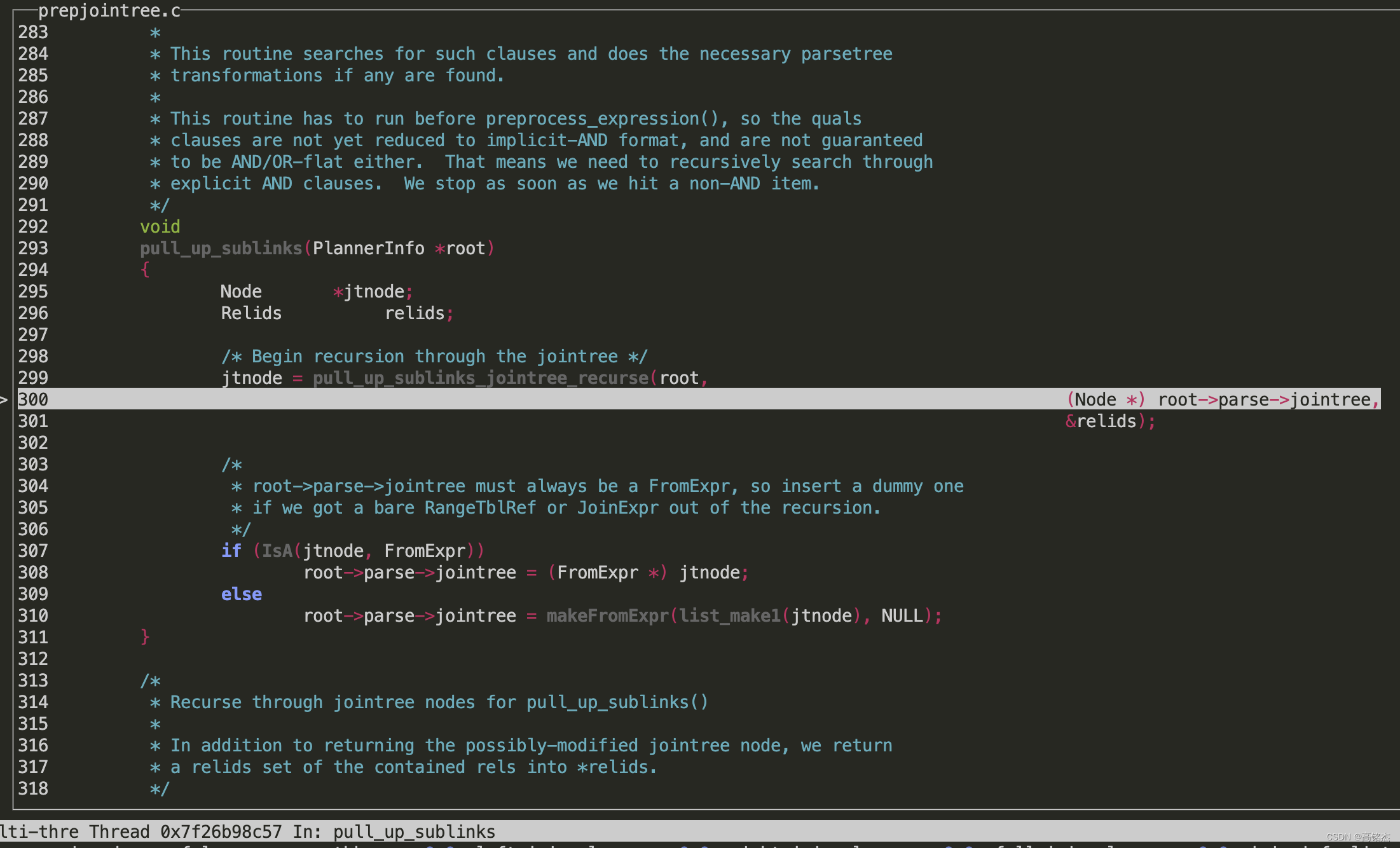
执行p elog_node_display(LOG, "parse tree", root->parse, true)

从日志中查看查询树，可以看到from的第二个子表是sublink。

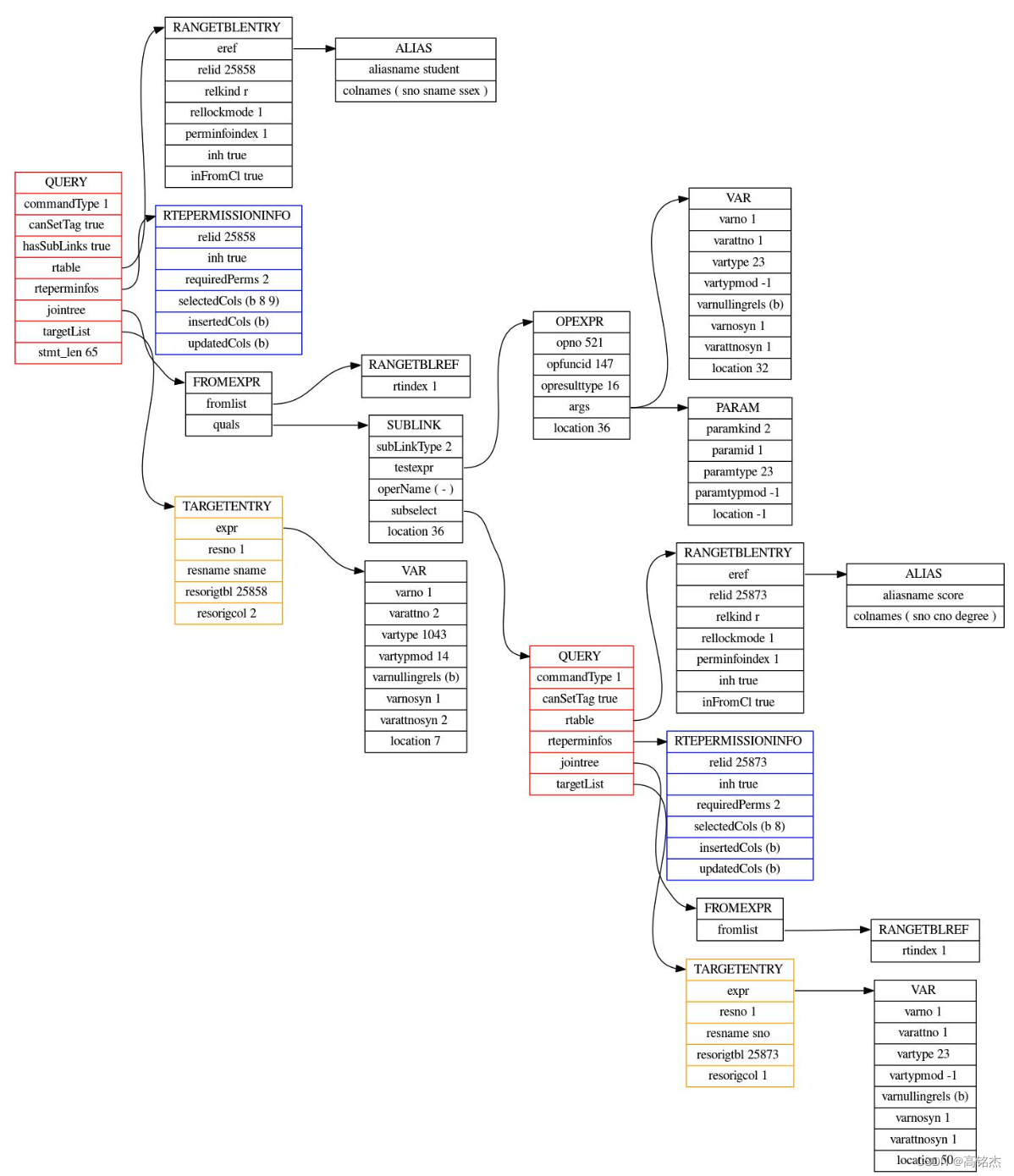
注意pull_up_sublinks_jointree_recurse函数需要的入参只有join tree就够了，从上图中可以看到根节点中的jointree。

void
pull_up_sublinks(PlannerInfo *root)
{
	Node	   *jtnode;
	Relids		relids;

	/* Begin recursion through the jointree */
	jtnode = pull_up_sublinks_jointree_recurse(root,
											   (Node *) root->parse->jointree,
											   &relids);

	/*
	 * root->parse->jointree must always be a FromExpr, so insert a dummy one
	 * if we got a bare RangeTblRef or JoinExpr out of the recursion.
	 */
	if (IsA(jtnode, FromExpr))
		root->parse->jointree = (FromExpr *) jtnode;
	else
		root->parse->jointree = makeFromExpr(list_make1(jtnode), NULL);
}

pull_up_sublinks_jointree_recurse会对join树进行递归分析，内部关键流程：convert_ANY_sublink_to_join。

3.2 谓词下推&等价类推理

下推是为了尽早地过滤数据，这样就能在上层结点降低计算量。

选择 (σ)
投影 (π)
自然连接 (⋈)
笛卡尔积 (x)
逻辑算子：∧（与）、∨ (或)、 ¬（非）

例如下面关系式：

Πcname,tname (σTEACHER.tno=5∧TEACHER.tno=COURSE.tno (TEACHER×COURSE))

翻译成SQL：
select cname,tname from teacher, course where teacher.tno=5 and teacher.tno=course.tno;

第一次优化：下推选择

Πcname,tname (
  TEACHER.tno=COURSE.tno (
    σTEACHER.tno=5(TEACHER)×COURSE
  )
)

第二次优化：下推投影

Πcname,tname (
  σTEACHER.tno=COURSE.tno 
    (Πtname,tno(σTEACHER.tno=5(TEACHER)) × Πcname,tno(COURSE)
  )
)

翻译成SQL

-- 下推前
SELECT cname,tname FROM 
  TEACHER t, COURSE c 
WHERE t.tno = 1 AND t.tno = c.tno;
 
-- 下推后
SELECT cname,tname FROM 
  (SELECT tname,tno FROM TEACHER WHERE tno = 1) tt, 
  (SELECT cname,tno FROM COURSE) cc 
WHERE tt.tno = cc.tno;

在PG中已经做过了优化，回得到相同的执行计划：

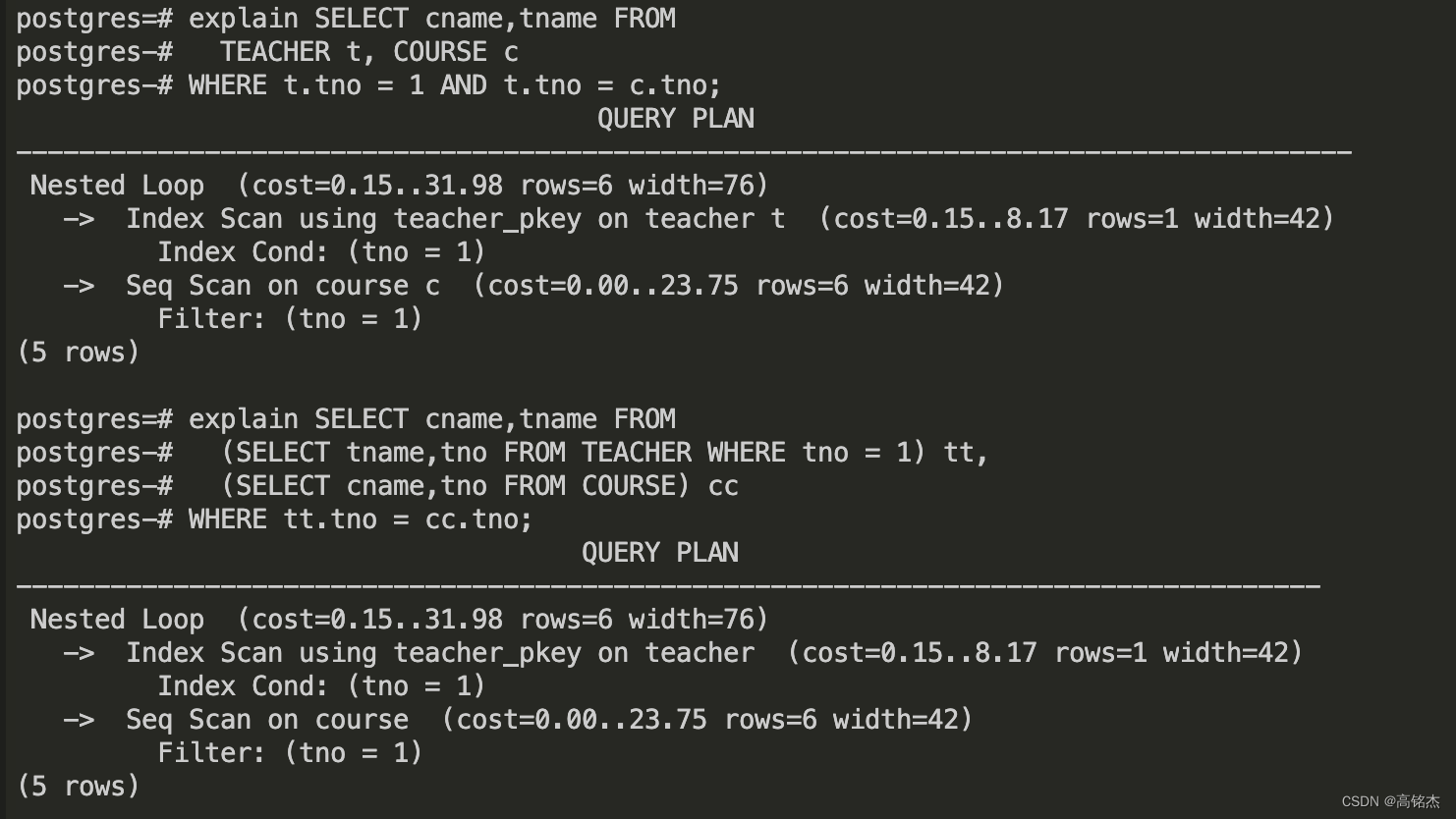
注意这里的course并没有选择条件，但seq scan course的计划中存在tno=1，这就是等价推理。