UnityVR--机械臂场景8-三自由度逆向解算3-应用在ABB机械臂网站首页 技术杂谈

UnityVR--机械臂场景8-三自由度逆向解算3-应用在ABB机械臂

唐小墨同学 2023-06-21 08:00:03

简介UnityVR--机械臂场景8-三自由度逆向解算3-应用在ABB机械臂

1. ABB机械臂形态

前文已经在Unity中，将3自由度机械臂的数学模型实现出来了，现在我们将它实际应用于机械臂中。选用的机械臂3D模型是ABB IRB 4600工业机器人，来自AssetStore。

（图片来自ABB官网）

1. ABB机械臂形态

模型中总共有六个旋转轴，为了继承上一章内容和分析方法，仅使用其中的3个自由度。

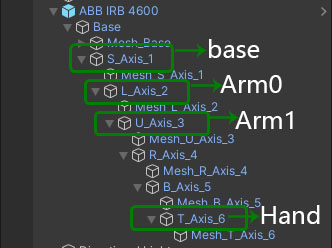
2. ABB机械臂数学模型分析

但是与上一章的数学模型不同的是，这里的base和Arm0两个节点坐标不同，因此在上一章的基础上，需要分两步来考虑：

第一步：以base为原点来计算θ3，这一步与上一章相同；

或者θ3=arctan(x/z)

第二步：以Arm0为原点计算θ1和θ2。

这里用二维图作示意，将坐标轴偏移一个距离，这时候Target的坐标变成了与Arm0节点的差值（x',y',z'）

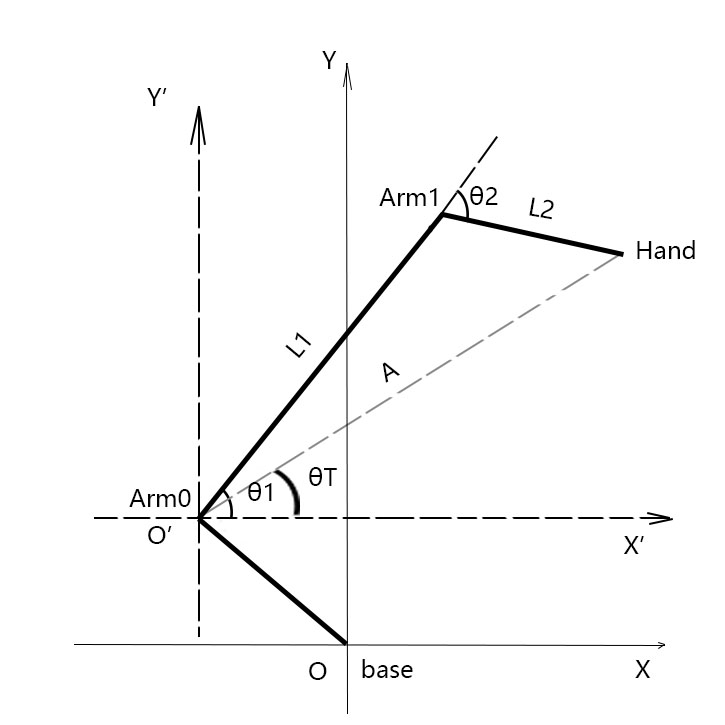
按照上一章的计算方式，重新计算W‘、A'、θT、θ2、θ1：

3. 初步程序实现

1. 准备工作：首先要拿到上述计算需要用到的变量：

    public Transform Base,Arm0,Arm1,Hand,Target;
    float X, Y, Z; //记录目标Target的位置，相对于Base
    float x_plus, y_plus, z_plus; //Target的位置，相对于Arm0
    private float L1,L2;
    private float sita_1, sita_2, sita_3, sita_T, W, A;

2. 准备工作：计算出L1、L2的值，这是固定不变的

        L1 = Vector3.Distance(Arm0.position, Arm1.position);
        L2 = Vector3.Distance(Arm1.position, Hand.position);

3. 先在以base为原点的坐标系中计算出θ3，套公式：

        X = Target.position.x - Base.transform.position.x;
        Y = Target.position.y - Base.transform.position.y;
        Z = Target.position.z - Base.transform.position.z;
        sita_3 = Mathf.Atan2(X, Z);
        sita_3 = Mathf.Rad2Deg * sita_3;

4. 再以Arm0为原点，计算x',y',z',W‘、A'、θT、θ2、θ1，套公式：

        x_plus = Target.position.x - Arm0.position.x;
        y_plus = Target.position.y - Arm0.position.y;
        z_plus = Target.position.z - Arm0.position.z;
        W = Mathf.Sqrt(square(x_plus) + square(z_plus));
        A = Mathf.Sqrt(square(W) + square(y_plus));
        sita_T = Mathf.Acos(W / A); 
        sita_1 = Mathf.Acos((square(L1) + square(W) + square(y_plus) - square(L2)) / (2 * L1 * A)) + sita_T;
        sita_2 = Mathf.Acos((square(W) + square(y_plus) - square(L1) - square(L2)) / (2 * L1 * L2));
        sita_1 *= Mathf.Rad2Deg;
        sita_2 *= Mathf.Rad2Deg;

好了，运行试试看：

结果中可以看到，虽然机械臂随着Target移动，但是却有一定的误差：Target和手爪之间错位了一段距离。这是为什么呢？下面分析一下误差产生的原因。

4. 误差分析

将这几个旋转节点单独拿出来观察，从XY平面来看，在机械臂的初始状态，Arm0到Arm1，以及Arm1到Hand，并不是完全地与Y轴平行的，XZ平面也是如此。这一点从Arm0和Arm1的本地坐标上也能看出来。但上述数学模型是简化了的，没有考虑到这些问题。

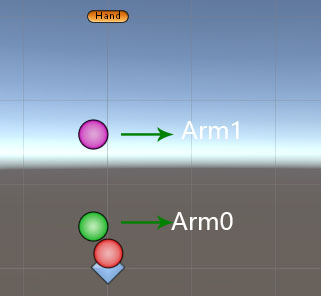
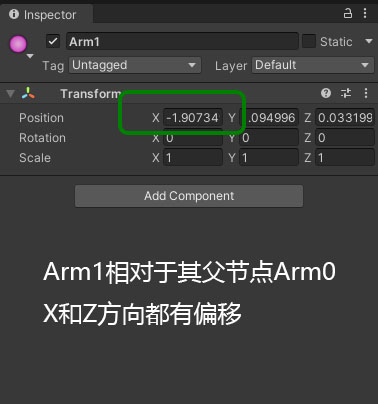
因此，在一开始还需要计算出初始角度，并在之后实际旋转时减去。sita_L1和sita_L2分别是两条手臂L1和L2的初始偏移角度。

        sita_L1 =(Mathf.Asin(Arm1.localPosition.x / L1))*Mathf.Rad2Deg;
        var temp = Hand.position.x - Arm1.position.x;
        sita_L2=(Mathf.Asin(temp/ L2)) * Mathf.Rad2Deg;

5. 最终实现

完整代码如下：

    public Transform Base,Arm0,Arm1,Hand,Target;
    float X, Y, Z; //记录目标Target的位置，相对于Base
    float x_plus, y_plus, z_plus; //Target的位置，相对于Arm0
    private float L1,L2;
    private float sita_1, sita_2, sita_3, sita_T, W, A;
    private float sita_L1, sita_L2;//L1、L2初始位置的偏移角
    void Start()
    {   //在ABB机械臂中，L1改成（S_Axis_2）到Arm1节点（U_Axis_3）的距离
        L1 = Vector3.Distance(Arm0.position, Arm1.position);
        L2 = Vector3.Distance(Arm1.position, Hand.position);

        sita_L1 =(Mathf.Asin(Arm1.localPosition.x / L1))*Mathf.Rad2Deg;
        var temp = Hand.position.x - Arm1.position.x;
        sita_L2=(Mathf.Asin(temp/ L2)) * Mathf.Rad2Deg;
        Debug.Log(String.Format("{0:N6}",sita_L1));//保留六位小数
        Debug.Log(String.Format("{0:N6}", sita_L2));
    }

    void Update()
    {
        X = Target.position.x - Base.transform.position.x;
        Y = Target.position.y - Base.transform.position.y;
        Z = Target.position.z - Base.transform.position.z;
        sita_3 = Mathf.Atan2(X, Z);
        sita_3 = Mathf.Rad2Deg * sita_3;
        Vector3 Euler3 = transform.localEulerAngles;
        Euler3.y = sita_3-90;//实际是从z轴正方向开始的旋转
        Base.transform.localEulerAngles = Euler3;

        //Sita_3旋转完成后，开始计算从Arm0为坐标原点的sita_1和sita_2
        x_plus = Target.position.x - Arm0.position.x;
        y_plus = Target.position.y - Arm0.position.y;
        z_plus = Target.position.z - Arm0.position.z;
        //重新计算W和A
        W = Mathf.Sqrt(square(x_plus) + square(z_plus));
        A = Mathf.Sqrt(square(W) + square(y_plus));  //A的长度=根号（W平方+Y平方）
        sita_T = Mathf.Acos(W / A);  //辅助角T
        sita_1 = Mathf.Acos((square(L1) + square(W) + square(y_plus) - square(L2)) / (2 * L1 * A)) + sita_T;
        sita_2 = Mathf.Acos((square(W) + square(y_plus) - square(L1) - square(L2)) / (2 * L1 * L2));

        sita_1 *= Mathf.Rad2Deg;
        sita_2 *= Mathf.Rad2Deg;

        Vector3 euler1 = Arm0.transform.localEulerAngles;
        euler1.z = -(90-sita_1+sita_L1);
        Arm0.localEulerAngles = euler1;
        Vector3 euler2 = Arm1.transform.localEulerAngles;
        euler2.z = -(sita_2- sita_L2);
        Arm1.localEulerAngles = euler2;
        Debug.Log("hand的位置:"+Hand.position);
    }
    static float square(float f)
    {
        return f * f;
    }

或者在旋转时加入球形插值，让它转得丝滑一些。