您现在的位置是:首页 >技术交流 >算法记录 | Day44 动态规划网站首页技术交流
算法记录 | Day44 动态规划
完全背包
有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。
完全背包和01背包问题唯一不同的地方就是,每种物品有无限件。
完全背包的物品是可以添加多次的,所以要从小到大去遍历
# 先遍历物品,再遍历背包
for i in range(len(weight)):
for j in range(weight[i],bagWeight+1):
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
# 先遍历背包,再遍历物品
for j in range(bag_weight + 1):
for i in range(len(weight)):
if j >= weight[i]: dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
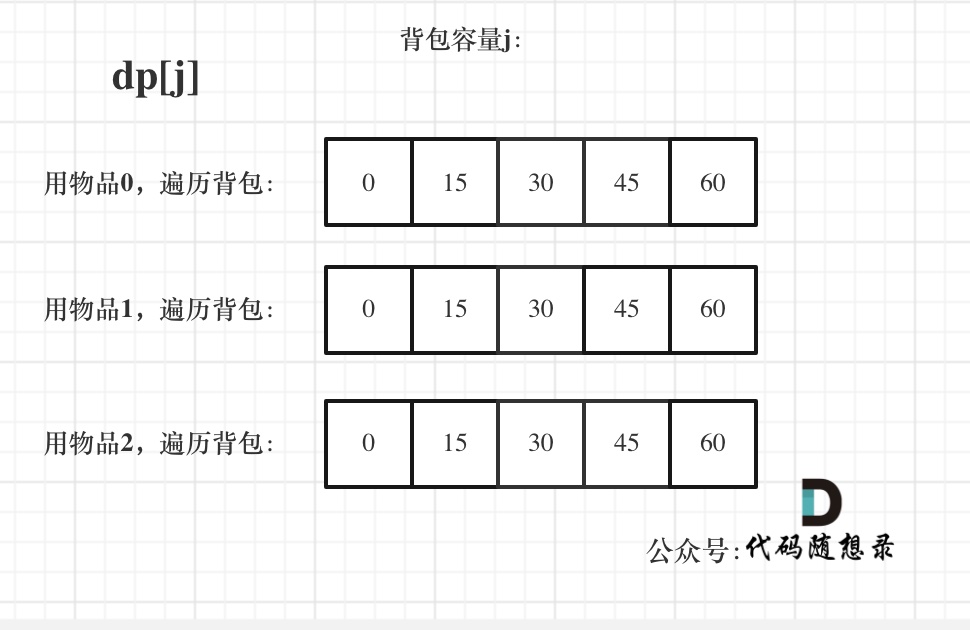
dp状态图如下:
518.零钱兑换 II
思路:
注意题目描述中是凑成总金额的硬币组合数。组合不强调元素之间的顺序,排列强调元素之间的顺序
1.确定dp数组以及下标的含义:dp[j]:凑成总金额j的货币组合数为dp[j]
2.确定递推公式:dp[j] = dp[j] + dp[j - coins[i]]
凑成总金额为 i 的方案数 = 「不使用当前 coin,只使用之前硬币凑成金额 j 的方案数」+「使用当前 coin凑成金额 j−coin的方案数」。
3.dp数组如何初始化:dp[0]=1,dp[0] = 1是 递归公式的基础。如果dp[0] = 0 的话,后面所有推导出来的值都是0了
4.确定遍历顺序:外层for循环遍历物品(钱币),内层for遍历背包(金钱总额),组合数;
外层for遍历背包,内层for循环遍历物品,排列数
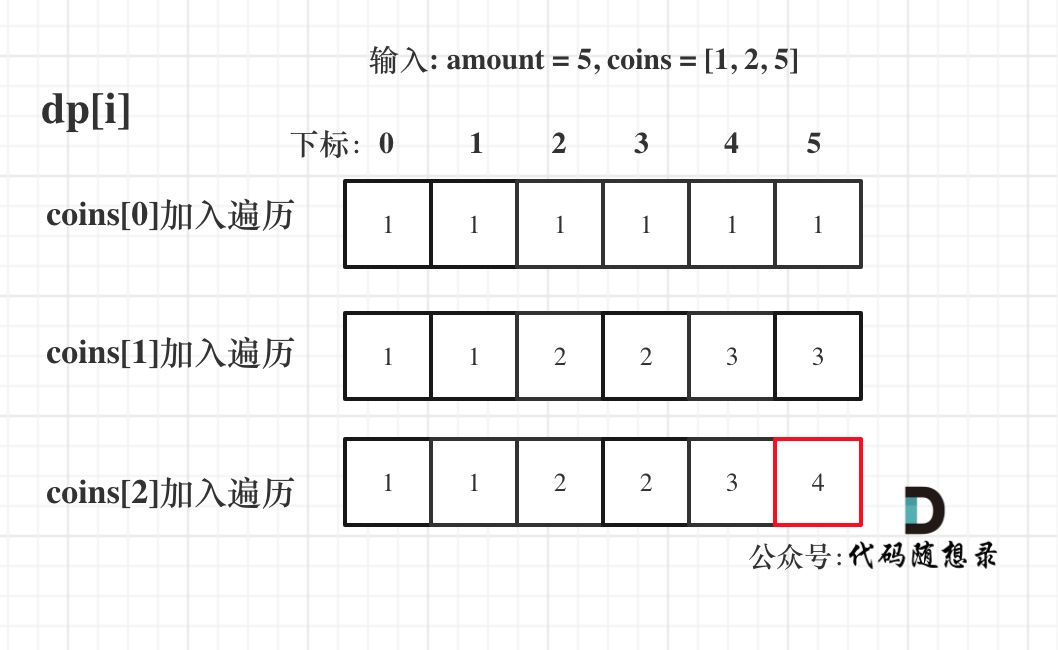
5.举例推导dp数组
输入: amount = 5, coins = [1, 2, 5] ,dp状态图如下:
class Solution:
def change(self, amount: int, coins: List[int]) -> int:
dp = [0 for _ in range(amount+1)]
dp[0] = 1
for i in range(len(coins)):
for j in range(coins[i],amount+1):
dp[j] = dp[j] + dp[j - coins[i]]
return dp[amount]
377.组合总和 Ⅳ
思路:
1.确定dp数组以及下标的含义:dp[i]: 凑成目标正整数为i的排列个数为dp[i]
2.确定递推公式:dp[i] = dp[i]+dp[i - nums[j]]
dp[i] =「不使用当前 nums[j]方案数」+「使用当前 nums[j]凑成 i - nums[j]的方案数」
3.dp数组如何初始化:dp[0]=1
4.遍历顺序 :求排列数就是外层for遍历背包,内层for循环遍历物品。
5.举例来推导dp数组
我们再来用示例中的例子推导一下:

class Solution:
def combinationSum4(self, nums: List[int], target: int) -> int:
dp = [0 for _ in range(target+1)]
dp[0] = 1
for i in range(1,target+1):
for j in nums:
if i >= j:
dp[i] += dp[i-j]
return dp[target]






 U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) Allegro16.6差分等长设置及走线总结
Allegro16.6差分等长设置及走线总结