【算法思维】-- 动态规划（C++）网站首页 学无止境

【算法思维】-- 动态规划（C++）

川入 2023-06-20 04:00:03

简介【算法思维】-- 动态规划（C++）

OJ须知：

一般而言，OJ在1s内能接受的算法时间复杂度：10e8 ~ 10e9之间（中值5*10e8）。在竞赛中，一般认为计算机1秒能执行 5*10e8 次计算。

时间复杂度 取值范围
o(log2n) 大的离谱
O(n) 10e8
O(nlog(n)) 10e6
O(nsqrt(n))) 10e5
O(n^2) 5000
O(n^3) 300
O(2^n) 25
O(3^n) 15
O(n!)
11

时间复杂度排序： o(1) < o(log2n) < o(n) < o(nlog2n) < o(n^2) < o(n^3) < o(2^n) < o(2^n) < o(3^n) < o(n!)

时间复杂度	取值范围
O(n)	10e8
O(nlog(n))	10e6
O(nsqrt(n)))	10e5
O(n^2)	5000
O(n^3)	300
O(2^n)	25
O(3^n)	15
O(n!)	11

Dynamic Programming

DP定义

动态规划是分治思想的延伸，通俗一点来说就是大事化小，小事化了的艺术。

融汇贯通的理解：

分治（大事化小，小事化了）：将问题进行分解，通过求解子问题，再用子问题推导大问题得解。

在将大问题化解为小问题的分治过程中，保存对这些小问题已经处理好的结果，并供后面处理更大规模的问题时直接使用这些结果。

DP具备了以下三个特点：

分解子问题：把原来的问题分解成了几个相似的子问题。（先求解最小的子问题）
求解子问题：所有的子问题都只需要解决一次。
保存子问题的解：按照需要储存子问题的解。（后序再以此推动，从而以子问题的解求取更大的子问题的解）

融汇贯通的理解：

DP VS 递归：递归中子问题的解一般是不保存的，而DP是需要保留结果的，有时候根据需要，有时候是部分的解，有时候甚至是保留全部的解。

动态规划的本质，是对问题状态的定义和状态转移方程的定义（状态以及状态之间的递推关系）

融汇贯通的理解：

状态的定义：子问题。

状态转移方程的定义：用子问题推大问题。

动态规划问题一般从以下四个角度考虑：

状态定义（根据题目的问题抽象而出）
状态间的转移方程定义（根据题目的问题的线索 + 状态定义 = 得出(≈递归方程)）
状态的初始化（一般就是最简单的子问题，不需要任何的推动，也不需要任何转移方程就可以将解确定出来）
返回结果（某一个状态的解 / 某几个状态处理的解）

状态定义的要求：定义的状态一定要形成递推关系。

一句话概括：三特点四要素两本质。

难点：

状态比较抽象，不好寻找
转移方程根据线索不好找

适用场景：

最大值 / 最小值
可不可行 / 是不是
方案个数

斐波那契数⭐

509. 斐波那契数 - 力扣（LeetCode）

斐波那契数（通常用 F(n) 表示）形成的序列称为斐波那契数列。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1

给定 n ，请计算 F(n) 。

提示：

0 <= n <= 30。

方法一：递归

class Solution {
public:
	int Fib(int n) {
		// 初始值
		if (n == 0) return 0;
		if (n == 1 || n == 2) return 1;

		// F(n) = F(n-1) + F(n-2)
		return Fib(n - 1) + Fib(n - 2);
	}
};

复杂度分析

时间复杂度：O(2^n)，随着n的增大呈现指数增长，效率低下当输入比较大时，可能导致栈溢出在递归过程中有大量的重复计算。（此处：0 <= n <= 30侥幸跑过)
空间复杂度：O(n)，为树的高度。

下图以求n = 4为例：

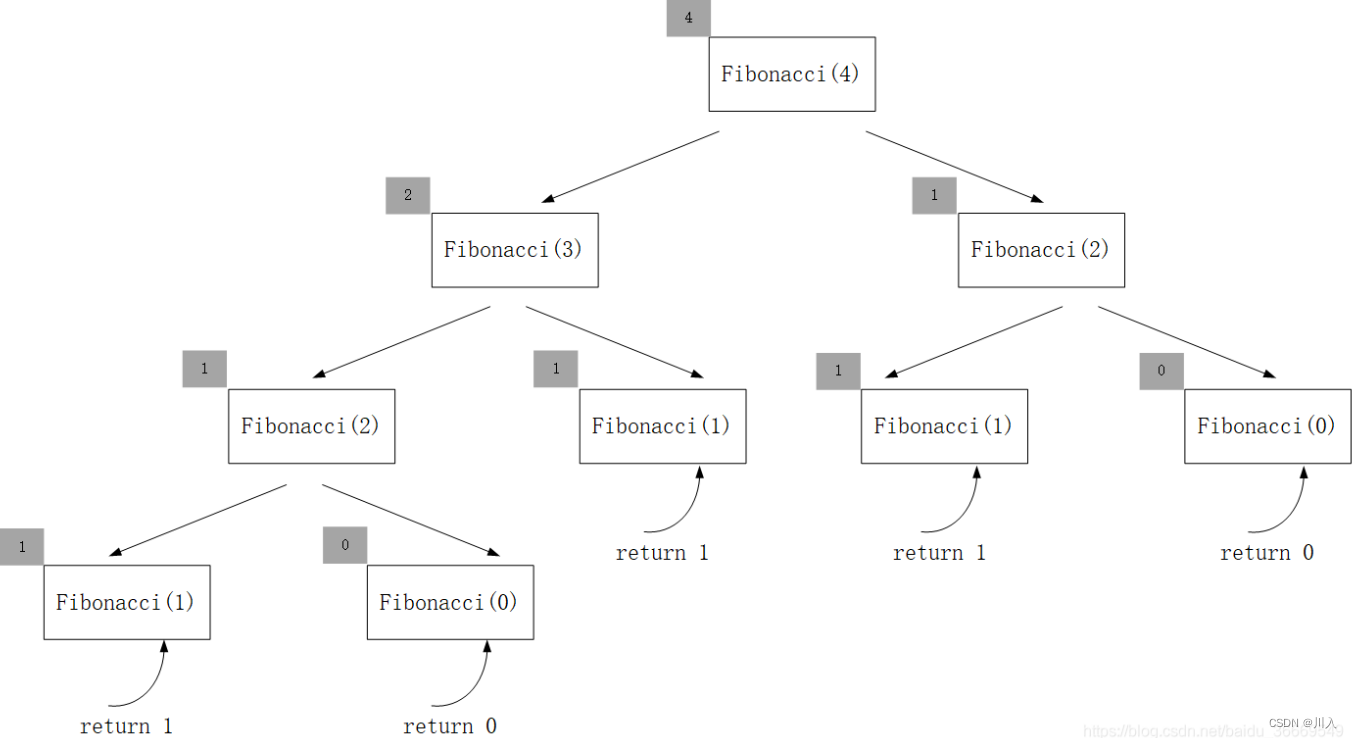
此处：1、根据C语言的函数栈帧开辟销毁特性；2、根据C语言语句执行先左后右的顺序。在语句：

return Fib(n - 1) + Fib(n - 2);

是先一路递归Fib(n - 1)后产生返回值并释放，才会再执行Fib(n - 2)。所以空间复杂度为树高：O(n)。

方法二：DP

引入DP四点：

状态定义（根据题目的问题抽象而出）
状态间的转移方程定义（根据题目的问题的线索 + 状态定义 = 得出(≈递归方程)）
状态的初始化（一般就是最简单的子问题，不需要任何的推动，也不需要任何转移方程就可以将解确定出来）
返回结果（某一个状态的解 / 某几个状态处理的解）

抽象题中线索：

状态定义：F(i) = ？
状态间的转移方程定义：F(i) = F(i - 1) + F(i - 2)
状态的初始化：F(0) = 0，F(1) = 1
返回结果：F(n) = ？

class Solution {
public:
    int fib(int n) {
        vector<int> v(n + 1, 0);
        v[0] = 0;
        if(n >= 1) v[1] = 1; // 题目中允许n = 0
        for(int i = 2; i <= n; i++)
            v[i] = v[i - 1] + v[i - 2];
        return v[n];
    }
}

经典的DP基础题，将每一个状态都进行保存，后面的状态都是通过前面已知状态结果，递推过来的。

复杂度分析

时间复杂度：O(n)。
空间复杂度：O(n)。

此处还可以对空间复杂度进行优化，因为求当前状态只需要前两个状态的结果，其余结果毫无用处。

class Solution {
public:
    int fib(int n) {
        if(n == 0) return 0;
        if(n == 1) return 1;
        int F_one = 0, F_tow = 1;
        int ret = 0;
        for(int i = 2; i <= n; i++)
        {
            ret = F_one + F_tow;
        // 更新中间状态
            F_one = F_tow;
            F_tow = ret;
        }
        return ret;
    }
};

时间复杂度：O(n)。
空间复杂度：O(1)。

单词拆分⭐⭐

139. 单词拆分 - 力扣（LeetCode）

给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。

s = "leetcode", wordDict = ["leet", "code"]

注意：不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。

提示：

1 <= s.length <= 300
1 <= wordDict.length <= 1000
1 <= wordDict[i].length <= 20
s 和 wordDict[i] 仅有小写英文字母组成
wordDict中的所有字符串 互不相同

方法一：DP

抽象题中线索：

状态定义：s 的前 i 个字符是否可以被分割
状态间的转移方程定义：s[0，n]能被分割，则s[n + 1，m]能否被分割，代表s[0，m]能否被分割(n < m)
状态的初始化：空字符串true（没有任何实际意义，就是辅助）
返回结果：s 是否可以被分割

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        // 状态定义：s 的前 i 个字符是否可以被分割
        vector<bool> ret(s.size() + 1, false);
        // 状态的初始化：空字符串true
        ret[0] = true;
        unordered_set<string> dict;
        for(int i = 0; i < wordDict.size(); i++)
            dict.insert(wordDict[i]);

        // 状态间的转移方程定义: s[0，n]能被分割，则s[n + 1，m]能否被分割，代表s[0，m]能否被分割(n < m)
        for(int m = 1; m <= s.size(); m++)
        {
            for(int n = 0; n < m; n++)
            {
                if(ret[n] && dict.end() != dict.find(s.substr(n, m - n)))
                {
                    ret[m] = true;
                    break;
                }
            }
        }
        // 返回结果：s 是否可以被分割
        return ret[s.size()];
    }
};

复杂度分析

时间复杂度：O(n^2)。
空间复杂度：O(n)。

三角形最小路径和⭐⭐

120. 三角形最小路径和 - 力扣（LeetCode）

给定一个三角形 triangle ，找出自顶向下的最小路径和。

每一步只能移动到下一行中相邻的结点上。相邻的结点在这里指的是下标与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说，如果正位于当前行的下标 i ，那么下一步可以移动到下一行的下标 i 或 i + 1 。

提示：

1 <= triangle.length <= 200
triangle[0].length == 1
triangle[i].length == triangle[i - 1].length + 1
-104 <= triangle[i][j] <= 104

方法一：DP

抽象题中线索：

状态定义：从 [ 0, 0 ] 到 [ i, j ] 的min = ?
状态间的转移方程定义：[ i, j ] += min([ i - 1, j - 1], [ i - 1, j ])（有些路径只有一条，代码里体现）

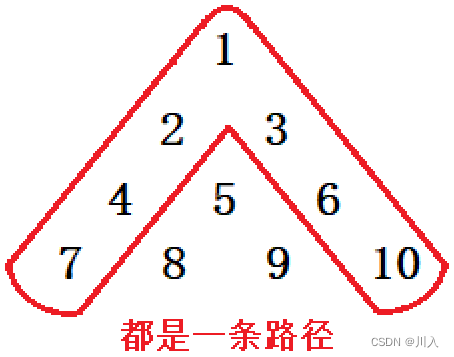
状态的初始化：[ 0, 0 ]的min = [ 0, 0 ]
返回结果：min ( [ 底行 ][ 0 ] ~ [ 底行 ][ 行底 ] )

class Solution {
public:
    int minimumTotal(vector<vector<int>>& triangle) {
        if(triangle.empty())
            return 0;
        int row = triangle.size();
        int col = triangle[row - 1].size();

        // 状态定义：从[ 0, 0 ]到[ i, j ]的min = ?
        vector<vector<int>> ret(row, vector<int>(col, 0));

        // 状态的初始化: [ 0, 0 ]的min = [ 0, 0 ]
        ret[0][0] = triangle[0][0];
        for(int i = 1; i < row; i++)
        {
            for(int j = 0; j <= i; j++)
            {
                // 状态间的转移方程定义: [i, j] += min([i - 1, j - 1], [i - 1, j])
                if(j == 0) ret[i][j] = ret[i - 1][j] + triangle[i][j];
                else if(j == i) ret[i][j] = ret[i - 1][j - 1] + triangle[i][j];
                else ret[i][j] = min(ret[i - 1][j], ret[i - 1][j - 1]) + triangle[i][j];
            }
        }
        // 返回结果: min([底行][0] ~ [底行][行底])
        return *min_element(ret[row - 1].begin(), ret[row - 1].end());
    }
};

复杂度分析

时间复杂度：O(n^2)，是一个2、3、4、5、6、7、8 …… row + 1的等差数列。
空间复杂度：O(n^2)。

进阶：

你可以只使用 O(n) 的额外空间（n 为三角形的总行数）来解决这个问题吗？

看上述代码，会发现我们根本就只是需要最后的一行数据，所以其实我们对于前述的二维数组，完全可以以一个以为数组代替。

class Solution {
public:
    int minimumTotal(vector<vector<int>>& triangle) {
        if(triangle.empty()) return 0;
        int row = triangle.size();
        int col = triangle[row - 1].size();

        // 状态定义：从[ 0, 0 ]到[ i, j ]的min = ?
        vector<int> ret(col, 0);

        // 状态的初始化: [ 0, 0 ]的min = [ 0, 0 ]
        ret[0] = triangle[0][0];
        for(int i = 1; i < row; i++)
        {
            for(int j = i; j >= 0; j--)
            {
                // 状态间的转移方程定义: [i, j] += min([i - 1, j - 1], [i - 1, j])
                if(j == 0) ret[j] = ret[j] + triangle[i][j];
                else if(j == i) ret[j] = ret[j - 1] + triangle[i][j];
                else ret[j] = min(ret[j], ret[j - 1]) + triangle[i][j];
            }
        }
        // 返回结果: min([底行][0] ~ [底行][行底])
        return *min_element(ret.begin(), ret.end());
    }
};

时间复杂度：O(n^2)，是一个2、3、4、5、6、7、8 …… row + 1的等差数列。
空间复杂度：O(n)。

方法二：DP（反向思维）

前面我们利用的解法，是这一行的解来自上一行的解，而这次我们反着，这一行的解来自下一行的解而不是上一行的解。

抽象题中线索：

状态定义：从 [ i, j ] 到 [ 底行, 行底 ] 的min = ?
状态间的转移方程定义：[ i, j ] += min([ i + 1, j ], [ i + 1, j + 1 ])（有些路径只有一条，代码里体现）

状态的初始化：[ 底行, 行底 ] 的 min = [ 底行, 行底 ]
返回结果：[0, 0]

class Solution {
public:
    int minimumTotal(vector<vector<int>>& triangle) {
        if(triangle.empty()) return 0;
        int row = triangle.size();
        int col = triangle[row - 1].size();
        vector<vector<int>> ret(row, vector<int>(col, 0));
        for(int i = 0; i<col; i++)
            ret[row - 1][i] = triangle[row - 1][i];

        for(int i = row - 2; i >= 0; i--)
        {
            for(int j = 0; j <= i; j++)
            {
                ret[i][j] = min(ret[i + 1][j], ret[i + 1][j + 1]) + triangle[i][j];
            }
        }
        return ret[0][0];
    }
};

复杂度分析

时间复杂度：O(n^2)，是一个2、3、4、5、6、7、8 …… row + 1的等差数列。
空间复杂度：O(n^2)。

不同路径⭐⭐

62. 不同路径 - 力扣（LeetCode）

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

提示：

1 <= m, n <= 100
题目数据保证答案小于等于 2*10^9

方法一：DP

抽象题中线索：

状态定义：从 [0，0] 到 [i，j] 有几种路径？
状态间的转移方程定义：[i，j] 路径 = [i，j - 1] 路径 + [i - 1，j] 路径
状态的初始化：第一行，第一列路径为1
返回结果：[底行, 行底]

class Solution {
public:
    int uniquePaths(int m, int n) {
        // 状态定义: 从[0，0]到[i，j]有几种路径？
        vector<vector<int>> ret(m, vector<int>(n, 0));

        // 状态的初始化: 第一行，第一列路径为1
        for(int i = 0; i < m ; i++) ret[i][0] = 1;
        for(int i = 0; i < n ; i++) ret[0][i] = 1;

        for(int i = 1; i < m ; i++)
        {
            for(int j = 1; j < n; j++)
            {
                // 状态间的转移方程定义: [i，j]路径 = [i，j - 1]路径 + [i - 1，j]路径
                ret[i][j] = ret[i][j - 1] + ret[i - 1][j];
            }
        }

        // 返回结果: [底行, 行底]
        return ret[m - 1][n - 1];
    }
};

复杂度分析

时间复杂度：O(m*n)。
空间复杂度：O(m*n)。

进阶：

你可以只使用 O(n) / O(m) 的额外空间来解决这个问题吗？

我们通过上述代码可以发现，[i，j] 的路径数只和 [i - 1，j] 与 [i，j - 1] 有关。也就是说其实我们可以利用一个一维数组就解决问题。比如以列为一维数组：vector<int> array(m, 1)，当列由第 i 列移动到 i + 1 列。

状态定义：从 [0，0] 到 [i，j] 有几种路径？
状态间的转移方程定义：[i] 路径(后) = [i - 1] 路径 + [i] 路径(前)
状态的初始化：第一列路径为1
返回结果：[列底]

class Solution {
public:
    int uniquePaths(int m, int n) {
        // 状态定义: 从[0，0]到[i，j]有几种路径？
        // 状态的初始化: 第一列路径为1
        vector<int> ret(m, 1);

        for(int i = 1; i < n; i++)
        {
            for(int j = 1; j < m; j++)
            {
                // 状态间的转移方程定义: [i]路径(后) = [i - 1]路径 + [i]路径(前)
                ret[j] = ret[j - 1] + ret[j];
            }
        }

        // 返回结果: [列底]
        return ret[m - 1];
    }
};

时间复杂度：O(m*n)。
空间复杂度：O(m)。

最小路径和⭐⭐

64. 最小路径和 - 力扣（LeetCode）

给定一个包含非负整数的 m * n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

提示：

m == grid.length
n == grid[ i ].length
1 <= m, n <= 200
0 <= grid[ i ][ j ] <= 100

方法一：DP

抽象题中线索：

状态定义：从 [0，0] 到 [i，j] min = ？
状态间的转移方程定义：[i，j] += min ([i，j - 1]，[i - 1，j])（有些路径只有一条，代码里体现）

状态的初始化：[0, 0] min = [0, 0]
返回结果：[底行, 行底]

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int row = grid.size();
        int col = grid[0].size();
        // 状态定义: 从 [0，0] 到 [i，j] min = ？
        vector<vector<int>> ret(row, vector<int>(col, 0));
        
        // 状态的初始化: [0, 0] min = [0, 0]
        ret[0][0] = grid[0][0];

        for(int i = 0; i < row; i++)
        {
            for(int j = 0; j < col; j++)
            {
                // 状态间的转移方程定义: [i，j] += min ([i，j - 1]，[i - 1，j])
                if(i == 0 && j > 0) ret[0][j] = grid[0][j] + ret[0][j - 1];
                else if(j == 0 && i > 0) ret[i][0] = grid[i][0] + ret[i - 1][0];
                else if(j > 0 && i > 0) ret[i][j] = min(ret[i][j - 1], ret[i - 1][j]) + grid[i][j];
            }
        }
        
        // 返回结果: [底行, 行底]
        return ret[row - 1][col - 1];
    }
};

方便看原理，下述代码将状态间的转移方程特殊情况，单独提出进行书写。

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int row = grid.size();
        int col = grid[0].size();
        // 状态定义: 从 [0，0] 到 [i，j] min = ？
        vector<vector<int>> ret(row, vector<int>(col, 0));

        // 状态的初始化: [0, 0] min = [0, 0]
        ret[0][0] = grid[0][0];

        // 特殊转换状态：第一行、第一列
        for(int i = 1; i < row; i++) ret[i][0] = grid[i][0] + ret[i - 1][0];
        for(int i = 1; i < col; i++) ret[0][i] = grid[0][i] + ret[0][i - 1];

        for(int i = 1; i < row; i++)
        {
            for(int j = 1; j < col; j++)
            {
                // 状态间的转移方程定义: [i，j] += min ([i，j - 1]，[i - 1，j])
                ret[i][j] = min(ret[i][j - 1], ret[i - 1][j]) + grid[i][j];
            }
        }
        // 返回结果: [底行, 行底]
        return ret[row - 1][col - 1];
    }
};

复杂度分析

时间复杂度：O(m*n)。
空间复杂度：O(m*n)。

进阶：

你可以只使用 O(n) / O(m) 的额外空间来解决这个问题吗？

此题与上一题极为的相似，所上一题采取的列解决，这一题就采取行解决。

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int row = grid.size();
        int col = grid[0].size();
        // 状态定义: 从 [0，0] 到 [i，j] min = ？
        vector<int> ret(col, 0);
        
        // 状态的初始化: [0, 0]min = [0, 0]
        ret[0] = grid[0][0];

        for(int i = 0; i < row; i++)
        {
            for(int j = 0; j < col; j++)
            {
                // 状态间的转移方程定义: [j] = min ([j]，[j-1]) + grid[i][j]
                if(i == 0 && j > 0) ret[j] = ret[j - 1] + grid[i][j];
                else if(j == 0 && i > 0) ret[j] = ret[j] + grid[i][j];
                else if(i > 0 && j > 0)ret[j] = min(ret[j - 1], ret[j]) + grid[i][j];
            }
        }

        // 返回结果: [底行, 行底]
        return ret[col - 1];
    }
};

时间复杂度：O(m*n)。
空间复杂度：O(n)。

背包问题⭐⭐⭐

125 · 背包问题（二） - LintCode

有 n 个物品和一个大小为 m 的背包，给定数组 A 表示每个物品的大小和数组 V 表示每个物品的价值。

问最多能装入背包的总价值是多大?

提示：

A[i], V[i], n, m 均为整数
你不能将物品进行切分
你所挑选的要装入背包的物品的总大小不能超过 m
每个物品只能取一次
m <= 1000，len(A)，len(V)<=100

方法一：DP

抽象题中线索：

状态定义：到第 i 商品的第 j 个空间 ret[i][j] 时的max价值 = ?
状态间的转移方程定义：

当前空间 j 不够放该商品，原封不动（上次商品的样子）：ret[i][j] = ret[i - 1][j]
当前空间 j 够放该商品（ max( (放入i + 剩余空间能放的max) , (前面 i-1) ) ）：ret[i][j] = max(ret[i - 1][j]，v[i - 1] + ret[i - 1][j - a[i - 1]])

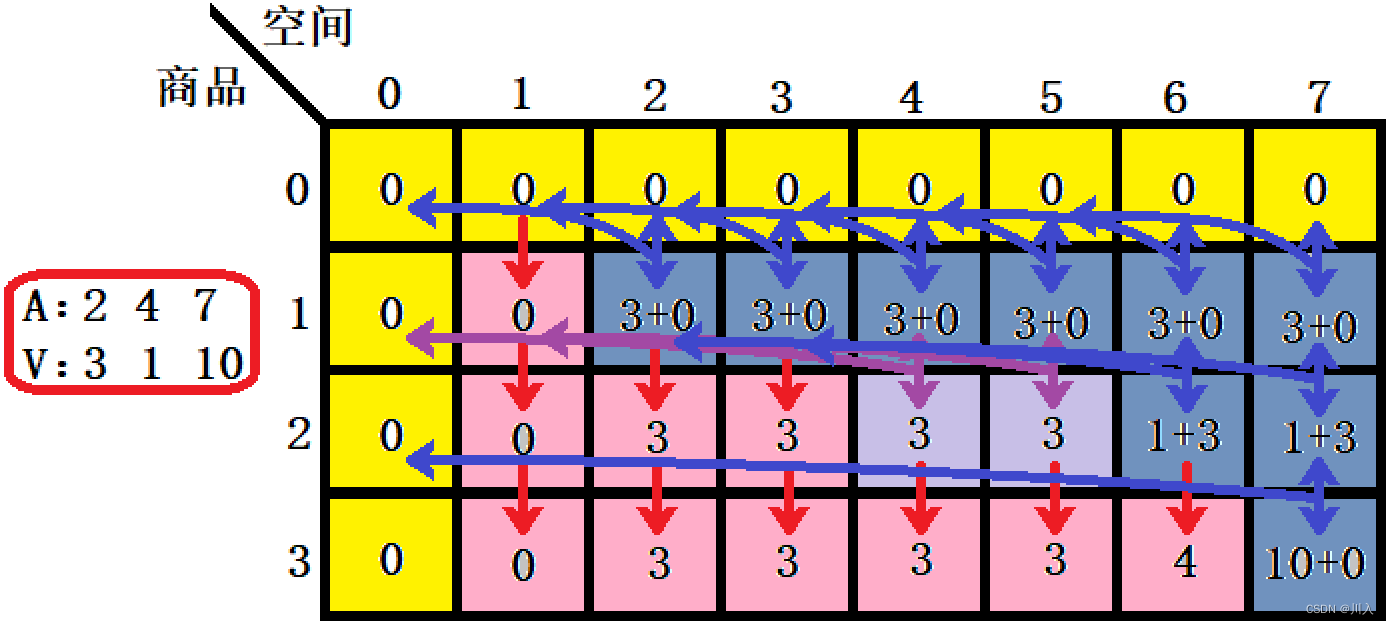
状态的初始化：没有商品 ret[0][j]max价值 = 0，没有空间 ret[i][0]max价值 = 0
返回结果：到第最后商品的第最后空间 ret[最后][最后] 时的max价值 = ?

class Solution {
public:
    /**
     * @param m: An integer m denotes the size of a backpack
     * @param a: Given n items with size A[i]
     * @param v: Given n items with value V[i]
     * @return: The maximum value
     */
    int backPackII(int m, vector<int> &a, vector<int> &v) {
        // write your code here
        // 状态定义: 到第 i 商品的第 j 个空间 ret[i][j] 时的max价值 = ?
        // 状态的初始化: 没有商品 ret[0][j]max价值 = 0，没有空间 ret[i][0]max价值 = 0
        vector<vector<int>> ret(a.size() + 1, vector<int>(m + 1, 0));

        // 状态间的转移方程定义: 
        for(int i = 1; i <= a.size(); i++)
        {
            for(int j = 1; j <= m; j++)
            {
                // 当前空间 j 不够放该商品，原封不动（上次商品的样子）: ret[i][j] = ret[i - 1][j] 
                if(a[i - 1] > j)
                    ret[i][j] = ret[i - 1][j];
                // 当前空间 j 够放该商品（ max( (放入i + 剩余空间能放的max) , (前面 i-1) ) ）: ret[i][j] = max(ret[i - 1][j]，v[i - 1] + ret[i - 1][j - a[i - 1]]) 
                else
                    ret[i][j] = max(ret[i - 1][j], v[i - 1] + ret[i - 1][j - a[i - 1]]);
            }
        }
        // 返回结果: 到第 最后 商品的第 最后 空间 ret[最后][最后] 时的max价值 = ?
        return ret[a.size()][m];
    }
};

复杂度分析

（m：背包大小；n：商品个数）

时间复杂度：O(m*n)。
空间复杂度：O(m*n)。

进阶：

你可以只使用 O(m) 的额外空间来解决这个问题吗？

我们可以发现，我们使用的仅仅就是 i -1 个商品时和 i 个商品时背包的状态。所我们可以将 m*n 变为 m*2，即：O(m)。

class Solution {
public:
    /**
     * @param m: An integer m denotes the size of a backpack
     * @param a: Given n items with size A[i]
     * @param v: Given n items with value V[i]
     * @return: The maximum value
     */
    int backPackII(int m, vector<int> &a, vector<int> &v) {
        // write your code here
        // 状态定义: 
        // 状态的初始化: 
        vector<vector<int>> ret(2, vector<int>(m + 1, 0));

        // 最后一组数据
        int row = 0;
        // 状态间的转移方程定义: 
        for(int i = 1; i <= a.size(); i++)
        {
            for(int j = 1; j <= m; j++)
            {
                row = i % 2;
                if(a[i - 1] > j)
                    ret[row][j] = ret[(row + 1)%2][j];
                else
                    ret[row][j] = max(ret[(row + 1)%2][j], v[i - 1] + ret[(row + 1)%2][j - a[i - 1]]);
            }
        }
        // 返回结果: 
        return ret[row][m];
    }
};

核心：

row = i % 2 是当前行
(row + 1) % 2 是上一行

待更……

风语者！平时喜欢研究各种技术，目前在从事后端开发工作，热爱生活、热爱工作。

上一篇
LeetCode第141题——环形链表（Java）...

下一篇
c# 根据CAD权籍数据的扩展属性，输出房地...

站长推荐

U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决
stm32使用HAL库配置串口中断收发数据（保姆级教程）
stm32使用HAL库配置串口中断收发数据（保姆级教程）
SpringSecurity实现前后端分离认证授权
SpringSecurity实现前后端分离认证授权
【社区图书馆】伴我前行的一本书《The C Programming Language》
【社区图书馆】伴我前行的一本书《The C Programming Language》
分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效)

时间复杂度	取值范围
o(log2n)	大的离谱
O(n)	10e8
O(nlog(n))	10e6
O(nsqrt(n)))	10e5
O(n^2)	5000
O(n^3)	300
O(2^n)	25
O(3^n)	15
O(n!)	11

您现在的位置是：首页 >学无止境 >【算法思维】-- 动态规划（C++）网站首页学无止境

【算法思维】-- 动态规划（C++）

Dynamic Programming

DP定义

斐波那契数⭐

方法一：递归

复杂度分析

方法二：DP

复杂度分析

单词拆分⭐⭐

方法一：DP

复杂度分析

三角形最小路径和⭐⭐

方法一：DP

复杂度分析

方法二：DP（反向思维）

复杂度分析

不同路径⭐⭐

方法一：DP

复杂度分析

最小路径和⭐⭐

方法一：DP

复杂度分析

背包问题⭐⭐⭐

方法一：DP

复杂度分析

上一篇 LeetCode第141题——环形链表（Java）...

下一篇 c# 根据CAD权籍数据的扩展属性，输出房地...

站长推荐

上一篇
LeetCode第141题——环形链表（Java）...

下一篇
c# 根据CAD权籍数据的扩展属性，输出房地...