😛作者：日出等日落

📘 专栏：数据结构

                                            把每天当作最后一天来过，那么你就能够学会珍惜。你珍惜了时间，时间自然会对你有所回报。

目录

 🎄堆的创建：

堆排序： 

向下调整的时间复杂度：

 向上调整的时间复杂度：

TOP-K问题： 

 🎄堆的创建：

这次是是对上一章节进行了优化，可以替换掉HeapInit函数

如需了解，请看http://t.csdn.cn/SEvl0这一文章，是堆的简单创建

//堆的创建
void HeapCreat(HP* hph, HPDataType* a, int n)
{
	assert(hph);
	hph->a = (HPDataType*)malloc(sizeof(HPDataType) * n);
	if (hph->a == NULL)
	{
		perror("malloc fail:");
		exit(-1);
	}
	memcpy(hph->a, a, sizeof(HPDataType) * n);
	hph->size = hph->capacity = n;

	//建堆算法
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)
	{
		AdjustDown(hph->a, n, i);
	}
}
//堆的销毁
void HeapDestory(HP* hph)
{
	assert(hph);
	free(hph->a);
	hph->a = NULL;
	hph->capacity = 0;
	hph->size = 0;
}
void TestHeap3()
{
	int array[] = { 27, 15, 19, 18, 28, 34, 65, 49, 25, 37 };
	HP hp;
	HeapCreat(&hp, array, sizeof(array) / sizeof(int));
	HeapPrint(&hp);

	HeapDestory(&hp);
}

堆排序： 

向上调整和向下调整的思想可以参考我的例外一篇博客：http://t.csdn.cn/kDcRa

实现堆排序：

向下调整优于向上调整（下面时间复杂度详解）

先利用Ajustdown排序好数组，然后再用交换Ajustdown实现小堆。

void HeapSort(HPDataType* a,int n)
{
	//这里采用向下调整O(n)
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)	
	{
		AdjustDown(a, n, i);
	}
	int end = n - 1;
	
	//N*O(m=n)
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		--end;
	}
}
void TestHeap4()
{
	int array[] = { 27, 15, 19, 18, 28, 34, 65, 49, 25, 37 };
	HeapSort(array, sizeof(array) / sizeof(HPDataType));
	for (int i = 0; i < sizeof(array) / sizeof(HPDataType); i++)
	{
		printf("%d ", array[i]);
	}
}

向下调整的时间复杂度：

//向下调整
void AdjustDown(HPDataType* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child + 1< n && a[child] > a[child + 1])
		{
			child = child + 1;
		}
		//child 大于 parent 就交换
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

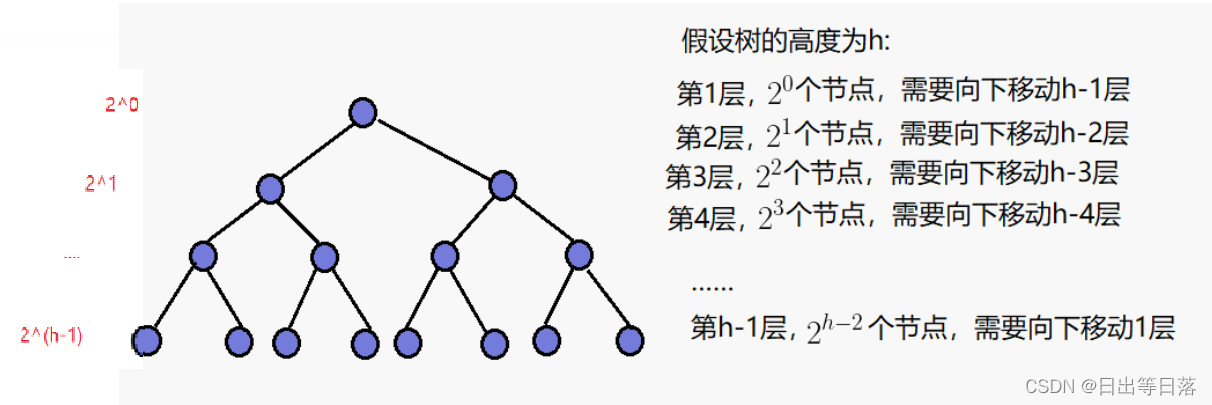
假设树高为h：

第一层有2^0个结点；

第二层有2^1个结点；

第三层有2^2个结点；

第h层有2^(h-1)个结点；

进行向下调整的时候要向下调整：

第一层要想下调整2^0*(h-1)次；

第二层要想下调整2^1*(h-2)次；

第h-1层要想下调整2^(h-2)*1次；

第h层要想下调整2^(h-1)*0次；

当h高的次数，最多调整层数为：

F(h)=                      2^(h-2)*1+2^(h-3)*2+..........+2^2*(h-3)+2^1*(h-2)+2^0*(h-1)       ——①

2*F(h)= 2^(h-1)*1+2^ (h-2)*2+2^(h-3)*3+.........+2^2*(h-2)+2^1*(h-1)      ——②

有错位相减②-①可得：

F(h)= 2^(h-1) + 2^(h-2) + 2^(h-3) +......+ 2^2 + 2^1 - h-1

F(h)=2^h-1-h                                                                                                           ——③

 当树高为h时，节点总个数N为：

N=2^0+2^1+...+2^（h-2）+2^（h-1）

N=2^h-1                                                                                                                        ——④

有④可得：h=log（N+1）                                                                                            ——⑤

综合③④⑤可得：

F（N）=N-log（N+1）

因此时间复杂度为O（N）

 向上调整的时间复杂度：

//向上调整
//child和parent都是下标
void AdjusUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child>0)
	{
		if (a[parent] < a[child])
		{
			Swap(&a[parent], &a[child]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

F(h)=2^1*1+2^2*2+....+2^(h-1)*(h-1)。

由错位相减可得：

F(N)=2N(1-log(N+1))

时间复杂度为O(N*logN)

TOP-K问题： 

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。

比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。

对于Top-K问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了(可能 数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决，基本思路如下：

• 用数据集合中前K个元素来建堆

1.   前k个最大的元素，则建小堆
2.   前k个最小的元素，则建大堆

• 用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素  将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K个最小或者最大的元素。

void TestHeap6()
{
	// 造数据
	int n, k;
	printf("请输入n和k:>");
	scanf("%d%d", &n, &k);
	srand(time(0));
	FILE* fin = fopen("Data1.txt", "w");
	if (fin == NULL)
	{
		perror("fopen fail");
		return;
	}

	int randK = k;
	for (size_t i = 0; i < n; ++i)
	{
        //随机数插入
		int val = rand() % 10000;
		fprintf(fin, "%d
", val);
	}

	fclose(fin);

	/
	// 找topk
	FILE* fout = fopen("Data1.txt", "r");
	if (fout == NULL)
	{
		perror("fopen fail");
		return;
	}

	//int minHeap[5];
	int* minHeap = malloc(sizeof(int) * k);
	if (minHeap == NULL)
	{
		perror("malloc fail");
		return;
	}

	for (int i = 0; i < k; ++i)
	{
		fscanf(fout, "%d", &minHeap[i]);
	}

	// 建小堆
	for (int i = (k - 1 - 1) / 2; i >= 0; --i)
	{
		AdjustDown(minHeap, k, i);
	}

	int val = 0;
	while (fscanf(fout, "%d", &val) != EOF)
	{
		if (val > minHeap[0])
		{
			minHeap[0] = val;
			AdjustDown(minHeap, k, 0);
		}
	}

	for (int i = 0; i < k; ++i)
	{
		printf("%d ", minHeap[i]);
	}
	printf("
");

	fclose(fout);
}
int main()
{
	TestHeap6();
	return 0;
}